变压器的负载运行
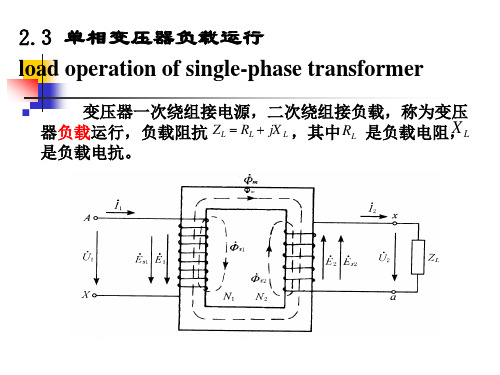
2.2变压器的负载运行

1、变压器带负载运行时,当负载增大(不考虑漏抗压降),则一次电流将,空载电流。
2、变压器带负载运行,当负载增大,则其铜损耗,铁损耗。
3、变压器由空载到满载,下列各物理量将如何变化(忽略漏抗压降),,,,。
4、变压器一次侧接额定电压,二次侧接纯电阻性负载,则从一次侧输入的功率。
(A)只含有有功功率;(B)只含有感性无功功率;(C)既含有有功功率又含有感性无功功率;(D)既含有有功功率又含有容性无功功率。
5、变压器负载时,一次磁动势为,一次漏磁通为,一次漏抗为;变压器空载时,一次磁动势为,一次漏磁通为,一次漏抗为,它们的关系是。
(A);(B);(C);(D)。
6、变压器负载()增加时,从理论上讲,其主磁通。
(A)稍增大;(B)稍减小;(C)增大很多;(D)减小很多。
7、电源电压一定时,试分析当变压器负载()增加时,如何变化?8、电源电压降低对变压器铁心饱和程度,励磁电流,励磁阻抗,铁耗和铜耗等有何影响?9、简述变压器空载和负载时,励磁磁动势有何不同?10、画出变压器的“T”形、近似和简化等效电路。
11、画出变压器简化等效电路和简化向量图。
12、画出变压器短路时的等效电路,并画出与之对应的向量图。
1、增大不变2、增大不变3、不变不变不变增大4、(C)5、(B)6、(B)7、答:降低。
由外特性曲线知,随负载电流()增大而下降。
增大。
负载越大,越大,由磁动势平衡方程式知,就越大。
不变。
大小与负载大小基本无关。
不变。
因电源电压不变,磁路饱和情况不变,故不变。
不变。
因漏磁路不饱和,。
8、答:铁心饱和程度降低。
,降低,减少,故饱和程度降低。
励磁电流减少。
由磁化曲线知,励磁电流随磁通减少而减少。
励磁阻抗增大。
励磁阻抗随饱和程度下降而增大。
铜耗减小。
电压降低,,减小,故铜耗减小。
铁耗减小。
,故铁耗减小。
9、答:,空载时I2=0,,所以空载时励磁磁动势仅为一次空载磁动势。
负载时,,励磁磁动势为一、二次的合成磁动势。
10、省略。
变压器的空载运行及负载运行

N1I0 N1 I0 N1 I1L N2 I2
N1 I1L - N2 I2
其中I1L远远大于I0,大部分用来抵抗副边电流引起的磁通量变化。
当负载运行时可认为I1L=I1。
I1
I2 k
或 I1 I2
1 k
N2 N1
k为变压器变比
一、二次电流比近似与匝数成反 比。可见匝数不同,不仅能改变 电压,同时也能改变电流。
产业信息
中国变压器设备-尤其是特种变压器-已 走向世界成为“中国制造” 品牌
谢谢聆听
P0 = PFe + Pcu ≈ PFe
铁损耗分量
铁损耗分量:符号为I10P,供给铁磁材料 铁损(磁滞和涡流损耗),为有功分量
Part 2 空载运行分析
思考
如果误将变压器高低压侧接反,会发生什么异常现象?
变压器低压侧如果接到高压电源上,则铁心主磁 通Φm会增加,磁路饱和程度增加,因而励磁电流I0大 大增加,有可能烧毁线圈(励磁电流随磁路饱和程度 增加而急剧增大)
单相变压器空载运行示意图
Part 2 空载运行分析
空载电流的作用与组成
I10 I10Q I10P
励磁分量
励磁分量:符号为I10Q,用来建立主磁 通,相位与主磁通相同,为无功分量
变压器空载运行时,只从电源吸收少量有功功率P0, 用来供给铁心中铁损PFe和少量绕组铜损Pcu=R1I102 (可忽略不计)。容量越大,空载功率P0越小
Part 3 变压器的负载运行
变压器作用 通过对变压器负载运行的分析,可以清楚地看出变压器具有变电压、 变电流、变阻抗的作用。
• 变换电压 U1/U2≈E1/E2=k=N1/N2
• 变换电流 I1/I2≈N2/N1=1/k
变压器经济运行负载率标准

变压器经济运行负载率标准
变压器的经济运行负载率标准因变压器类型、额定容量、使用环境等因素而异。
一般来说,变压器的经济运行负载率在50%~80%之间,以保证变压器的正常运行和寿命。
如果负载率过低,变压器可能会出现过载现象,导致温升过高、油漏、绕组烧毁等故障。
如果负载率过高,变压器可能会过热、损耗过大,缩短使用寿命。
具体来说,对于民用建筑中常用的双绕组变压器,其经济运行负载率通常在75%左右。
而在其他类型的变压器中,如配电变压器、居民住宅小区配电变压器等,其经济运行负载率会因具体标准和要求而有所不同。
因此,在实际应用中,需要根据变压器的具体情况和实际需求来确定其经济运行负载率标准,以保证变压器的安全、经济、高效运行。
3.3单相变压器的负载运行
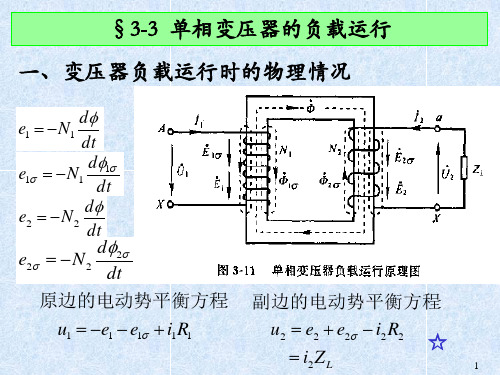
e1
N1
d
dt
e1
N1
d1
dt
e2
N2
d
dt
e2
N2
d2
dt
原边的电动势平衡方程: 副边的电动势平衡方程:
u1 e1 e1 i1R1
u2 e2 e2 i2R2 ☆
i2ZL
1
§3-3 单相变压器的负载运行
二、负载运行时的基本方程式
18
解 :(1)原、副边线电流: 变压器变比:
k U1N / 3 10000 25 U2N / 3 400
负载阻抗折算值:
ZL k 2ZL 252 (0.2 j0.07) 125 j43.75Ω
每相总阻抗:
Z zk ZL 1.546 j5.408125 j43.75Ω 126.546 j49.158 135.7621.23
X 2 k 2 X 2 3 0.055 0.165Ω
ZL k 2ZL 3 (4 j3) 12 j9Ω
14
根据题意,画出T形等值电路:
励磁阻抗:
Zm Rm jX m 30 j310 311.484.5
15
副边漏阻抗和负载阻抗和:
Z Z2 ZL 0.105 j0.165 12 j9 15.1837.1
『补例3-4』一台三相变压器,Y/y连接,SN=800kVA,U1N/U2N
=10000/400V;已知每相短路电阻rk=1.546,短路电抗xk=5.408
,该变压器原边接额定电压,副边接三相对称负载运行,每
相负载阻抗为:ZL=0.20+j0.07 。试用简化等值电路计算:
(1)变压器原、副边线电流; (2)副边线电压; (3)输入输出的有功功率及无功功率 (4)变压器效率
2-变压器负载运行
的大小
与空载运行时相比,负载时一次绕组的电流变化了,电源电压
不变,严格说来,负载时的
•
E
与空载时的不同。但在电力变压
1
器仍的然设还计是I中1N Z1I•0很U1小.仍,即存使在在U1额 E定1 由负载E1下 4运.44行fN1,I1Nm
比I0 大很多倍, 看出,空载、负
载与表运示空行。载,时其的主在磁数通值• m上的差数不值多差,仍别可很以小用,即同负一载个时符的号励I•磁0 N磁1或动势F• 0
因
,可认为 Zm
Z
' 2
Z
' L
无限Zm大而断开,于是等效电路变成了“一”型,
称为简化等效电路。如图:
单相变压器的负载运行
b.电压平衡方程式:
•
•
•
•
•
•
•
•
U1
I1
Z1
I 1 Z2'
U
' 2
I1
Z1
Z
' 2
U
' 2
I1 Zk
U
' 2
•
•
I1
I
' 2
•
•
U
' 2
Z
' L
单相变压器的负载运行
b.变压器接感性负载的相量图2-12a图:
单相变压器的负载运行
※相量图的绘制过程: 根据给定的条件不同,画法不同,但都是电压方程式 的相量图表示。
如给定U2, I2,cos2, k 及各参数,画图步骤为:
(((((((1234567)))))))根画在画画画E•1 据出出出出U•2'EU超•I2•'的•20' IE••前21相和E,•1,E量•910它/加I上Z•2的' m与,上,,主I其•I•1加画磁0R夹1上出通的,I角•2'U•相R•1再m为2' I量•,0加;和再上,2为加。它j上II••超11XjI•1;2前'得X2'到得•一m 出U•个1E•。2'铁耗;角;
变压器负载运行的工作原理

变压器负载运行的工作原理变压器是电力系统中必不可少的设备之一,其主要作用是将高电压的电能转换成低电压的电能,或者反之。
变压器的运行必须有负载,负载是指变压器的终端接有电动机、照明和其他电气设备等,从而使变压器运行并供电。
变压器的负载运行涉及到很多因素,本文将详细介绍变压器负载运行的工作原理。
一、变压器的结构和工作原理变压器是通过共同绕制在一个铁心上的两个电磁线圈来实现电能的转换。
一个线圈为主绕组,另一个线圈为副绕组。
主副绕组之间通过铁心磁路相联。
当主绕组接通电源时,会在铁心上产生一个磁场,这个磁场将副绕组中的电流感应出来,从而实现电能的转换。
变压器的基本结构如下图所示:在运行过程中,变压器主副绕组的电流大小要满足磁路平衡条件,即主副绕组的互感系数乘以电流大小相等。
变压器的运行中,主要有两种状态:空载和负载。
二、变压器的空载工作状态当变压器处于空载状态时,也就是没有负荷接在副绕组上,此时主绕组的电流非常小,基本上可以忽略不计。
在这种情况下,变压器的磁路中只有主绕组的电流存在,因此铁心中产生的磁通量和电流成比例。
变压器的空载工作状态如下图所示:由于变压器的主副绕组通过铁心磁路相联,因此副绕组中的电流也不能为0,必须满足磁路平衡条件。
但是由于此时副绕组没有外部负载,因此只能自激磁或感应磁通量。
三、变压器的负载工作状态当有负载接在变压器的副绕组上时,副绕组中就会有电流流过。
电流在副绕组中产生的磁场会和原来主绕组所产生的磁场相互作用,从而导致铁心中磁通量的变化。
这样就会引起主绕组中的电流和电压的变化,同时变压器也会供电给外部负载。
变压器的负载工作状态如下图所示:在变压器运行的负载工作状态下,铁心中产生的总磁通量不仅取决于主绕组中的电流,还与副绕组中的电流有关。
在这种情况下,变压器必须满足以下的条件:1. 主副绕组的电流在一定程度上应该成比例;2. 主副绕组的电压应当成比例。
四、变压器的负载特性在变压器的负载工作状态下,变压器的输出电压和电流都是按照一定的规律变化的。
变压器的负载运行解读

(3-39)
折算后,变压器负载运行时的基本方程式组可简化为如下的方程式组
U1 E1 I1z1 E1 I0zm U2 E2 I2 z2 U2 I2 zL E2 E1 I1 I2 I0
(3-40)
变压器的负载运行(续8)
2.等效电路
在将变压器副绕组的匝数折算为
与原绕组的匝数相等后,原、副绕组
负载增加时,I2 增加,副边磁动势N1 I2N2 增加,原
边电流的负载电流分量(-
N• I2
2
)也相应增加,
N
使 的其副产边生磁的动磁势动I2N势2 ,(以-维持NN12 I• 2励)磁1 Nl电得流以分抵量消增I0 加不了
变。可见,虽然变压器的原、副边没有直接的电
路联系,但负载电流的变化也会使原边电流相应
衡方程式。
变压器的负载运行(续2)
将磁动势平衡方程式表示成电流的形式,得
I
•
I
0
(
N
2
•
I2)
(3-26)
1
N
由上式看出,变压器负1 载运行时的原边电
流 I1 是大于变压器空载运行时的原边电流 I0 的, 它由反映主磁通 m 大小的励磁电流分量 I0 和反
映负载大小的负载电流分量(-
)组成。当 N • I2 2
s
s
s
图3.9 单相变压器负载运行 时的简化等效电路
变压器的负载运行(续9)
==308.00V例53/111,5已V其知,负一r1=载台0阻单.1抗相5为变,:压r2z器=L=的0.40数+2j43据为,。:x当S1N=外4.06k加.V2A7电,U压,1N /为xU22N 额定值时,用简化等效电路计算原、副边电流及副边电
变压器负载运行电磁关系要点

1. 磁动势平衡关系
r I 1 1
I 1
I N F 1 1 1
1
E 1
E 1
U 1
F F I N F 1 2 0 0 1
I 2 I N F 2 2 2
E 2
2
E 2
r I 2 2
U 2
I 2 I 1 k
I 1 1 I k 2
I1 1 N 2 I 2 k N1
结论:变压器原、副边电流与其匝数成反比, 当负载电流增大时,原边电流将随着增大,即输出 功率增大时,输入功率随之增大。 所以变压器是一个能量传递装置,它在变压 的同时也在变流。
E 2
2
E 2
r I 2 2
U 2
1. 磁动势平衡关系
r I 1 1
I 1
I N F 1 1 1
1
E 1
E 1
U 1
F F I N F 1 2 0 0 1
I 2 I N F 2 2 2
E 2
2.2.1 变压器负载运行电磁关系
变压器负载运行:指变压器原边绕组接额定电压、额 定频率的交流电源,副边绕组接负载时的运行状态。
I 1
~
0 I 2
1
E 2
~
E 1 U 1
E 1
2
E 2
U 2
ZL
图2-3
变压器负载运行时的示意图
一、负载时电磁关系
2
E 2
r I 2 2
U 2
变压器空载运行时, I 2 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E2' kE2
U
' 2
kU2
13
(3)漏抗
X
' 2
,(漏磁无功损耗不变)
I
'2 2
X
' 2
I22 X2
X
' 2
(I2
I2' )X 2
k2X2
(4)电阻 R2'
R2'
I
'2 2
I
2 2
R2
R2' k 2R2
14
能量是否改变?
铜耗: mI2' 2Rr22'' mI22rR22
有功输出:
mU
' 2
I
' 2
cos2
mkU2
1 k
I2
cos2
mU 2 I 2
cos2
无功输出:
mU2'
I
' 2
sin 2
mkU2
1 k
I2
sin 2
mU 2 I 2
sin 2
15
折算法只是一种分析的方法 凡是单位为伏的物理量(电动势、电压)的折算
值等于原来数值乘k; 单位为欧的物理量(电阻、电抗、阻抗)的折算值 等于原来数值乘k2; 电流的折算值等于原来的数值乘以1/k。
副边:
•
••
•
U 2 E 2 E 2 I 2 R2
用漏抗压降表示
•
•
•
••
E 2 j I 2 X 2 I 2 R2 E 2 I 2 Z2
A i1
u1 X
e1 e1
W1 W2
1 2
i2
a
e2 e2u2
ZL
x
7
2、负载时的电磁关系
•
•
•
U1
I1
I 1 W1
•
•
I2
I 2 W2
•
1
•
•
2
W1的电阻
变压器原边和副边没有直接电路的联系,只有磁 路的联系。副边的负载通过磁势影响原边。 因此 只有副边的磁势不变, 原边的物理量没有改变。 这为折算提供了依据。
这种保持磁势不变而假想改变它的匝数与电流 的方法,称折合算法。
10
2、定义:
将原、副边匝数变成同一匝数。 k 1(W1 W2)
实际绕组的各个量,称为实际值;假想绕组的各 个量,称为折算值;
•
•
E2'
U
' 2
•
I1
R1
•
U1
X1
X
' 2
•
R2' I2'
•
I0
Rm
Xm
•
U
' 2
T(型等效电路)
18
注: (1)电路中全部的量和参数都是每一相的值。原 边为实际值,副边为折算值。
原边绕组从电网吸收的功率传递给副边绕组。 副边 绕组电流增加或减小的同时,引起原边电流的增加或 减小,吸收的功率也增大或减小。
A i1
u1 X
e1 e1
W1 W2
1 2
i2
a
e2 e2u2
ZL
x
6
二、 电势方程式
1、电压方程:原边:
•
U
1
•
E1
•
E 1
•
I1
R1
•
•
•
••
E1 j I 1 X1 I 1 R1 E1 I 1 Z1
I0
•
I1L
W2
可见当付方电流发生变化时原边电流亦在变。
原边电流由两部分组成:
(1):I• 0 用以建立 主磁通
(2):I• 1L 负载分量
A i1
u1 X
e1 e1
W1 W2
1 2
i2
a
e2 e2u2
ZL
x
5
(3)能量传递:•
I1
•
I0
( W1 W2
)
•
I
2
•
I0
•
I1L
从空载到负载,原边绕组电流 I1增加一个分量I1L以 平衡副边绕组的作用
12
4、方法:(将付边各量折算到原边)
(1)副边电流
•
I
' 2
(磁势不变)
W2'
•
I
' 2
W2
•
I
2
•
•
I
' 2
W2
•
I2
I2
W1
k
(2)副边电势 E2' , E2' :(主磁通不变)
E'2 4.44 fW2'm W1 E2 4.44 fW2m W2
E2' kE2 E1
E'2 4.44 fW2'm W1 k E2 4.44 fW2m W2
2-2 变压器的负载运行
I&1
A
U&1 e1 E&1
X
&s11
W1
2&s 2
W2
i2
a
e2 e2u 2
ZL
x
1
[基本电磁关系列方程式等效电路图]
一、 负载时的磁势和原付边的电流关系
•
付边绕组接上负载阻抗ZL,有电流 I 2
•
•
•
•
I 2 F 2 W2 I2 2 (E 2 )
产生
A u1
X
i1 e1 e1
W1 W2
1 2
i2
u2 a
e2 e2
ZL
x
2
与空载时比较
(1)负载时的磁势
总磁势 空载磁势:
•
••
•
•
F m F 1 F 2 W1 I 1 W2 I 2
•
•
F m0 W1 I 0
A i1
u1 X
e1 e1
W1 W2
1 2
i2
a
e2 e2u2
ZL
x
3
(2)负载时的 电流:
U1 E1 4.44 fW1m
I1
R1
X1
•
•
I0
R2 X2 I2
k E1 W1
•
E2 W2
U1
无法构成一
•
Rm
•
E1
E2
•
U2
Xm
等效电路的
原因在于:
•
E1
•
E2
若k
1,
•
E1
••
E 2; I1
•
I0
•
I
2
9
三、绕组折算:
1、目的:变压器中, k 1, E1 E2, 无法构成一个完 整的回路。计算时相当复杂。为了解决这个矛 盾,引入绕组折算。
当U不变时, m C Fm C
故:W1
•
I 1 W2
•
I2
W1
•
I0
或: •
•
•
W1 I 1 W1 I 0 ( W2 I 2 )
A i1
u1 X
e1 e1
W1 W2
1 2
i2
a
e2 e2u2
ZL
x
4
•
•
•
W1 I 1 W1 I 0 ( W2 I 2 )
•
I1
•
I0
(
W1
)
•
I
2
•
16
折算后变压器的基本方程式:
•
••
U1 E1 I1(R1 jX1 )
• • •
U
' 2
E2'
I
' 2
(
R2'
jX
' 2
)
•
I1
•
I0
•
I
' 2
•
E1
•
E2'
• E1
II••00
Zm
•
I0(Rm
jXm )
•
••
U1 E1 I1(R1 jX1)
••
E1 I1 Z1
• ••
保持副边绕组的磁势不变进行折算, 称为副边向 原边折算;
保持原边绕组的磁势不变进行折算, 称为原边向 副边折算。
11
3、原则:
副边折算导原边 原边折算到副边
W2' W1 W1' W2
必须保持折算前后的电磁关系不变。在保持磁 势、磁通、功率、损耗及漏磁场储能不变时才 能折算,折算后值用“`”号表示。
U 2 E 2 I 2(R2 jX2 )
•
•
I1
•
I
0
(
I2 k
)
k E1 W1 E2 W2
••
•
E1 I 0 Zm I 0(Rm jXm )
17
四、等效电路
•
•
I1
•
I0
I
2
)
•
I1
•
I0
•
I
' 2
k
•
I1
R1
X1
•
I0
•
•
•
E1
Rm
U1
E1
•
E2'
Xm
X
' 2
•
R2'
I
' 2
•
I 1 R1
•
E 1
•
E1
•
E2
•
E 2
