第3章 剪切与圆轴扭转-new2
合集下载
第3章剪切和扭转

3.5 薄壁圆筒的扭转
为了研究圆轴扭转时的应力和变形,首先
讨论薄壁圆筒的扭转,以了解剪应力及剪应
变的规律和它们之间的关系。
一、薄壁圆筒扭转时的应力
t
j R
dq
R
R
图为一等截面薄壁圆筒。 在两端施加外力偶矩后,可以看到以下变形现象: (1)各周向线的形状、大小和间距均未改变,两相 邻周向线发生相对转动; (2)各纵向线都倾斜了同一微小角度 ,但仍可以 近似地看成直线; (3)试件表面原来的小矩形都变成了同样大小的平 行四边形。
一、圆轴扭转的破坏形式
(a)
45
(b )
三、破坏原因分析 圆轴扭转时,横截面上剪应力最大,而45°斜截面上拉应力最大。由此可对不同材料 的扭转破坏现象作出解释:对于铸铁,抗拉能 力最弱,扭转时,将沿着最大拉应力面被拉 断;对于低碳钢,其抗剪能力较差,故在剪应 力最大的横截面上被剪坏。
max 45
许用剪应力 ,即
Q A
(3-2)
这就是剪切强度条件。 若材料的极限剪应力 u , n为安全系数 则材料的许用剪应力 [ ] ,即
u
n
实验结果表明,材料的剪切强度极限与拉压强度极限有 近似比例关系: 塑性材料: (0.6 0.8)[ ] 脆性材料: (0.8 1.0)[ ] 估算剪切许用应力 的值。
max
转/分。 当功率为 N H 马力(H.P,1马力=735.5W)时,外 力偶矩的计算公式为
NH M e 7024 ( N m) n
(3-7)
二、扭矩和扭矩图 从指定截面m-m处截开,取左半部分I 由平衡条件
Mn Me 0
得
材料力学-第三章 扭转和剪切

max
M x max Wp
1 . 98 10 3 97 . 5 M P a 6 20 . 3 10
m a x 9 7 . 5
此轴满足强度条件
© 2012.Wei Yuan. All rights reserved.
2.两轴强度相等,故:
Me Me
max
© 2012.Wei Yuan. All rights reserved.
MeA=1591.5N· m
MeC=MeB=477.5N· m Mx(N· m)
MeD=636.5N· m
636.5 x
MeB
MeC MeA MeD
477.5
955
Mx(N· m) MeB
MeC
MeD
MeA
x 477.5
955 1591.5
剪切弹性模量 剪变模量
§3.4 圆轴扭转时的 应力与强度条件
n m
R
© 2012.Wei Yuan. All rights reserved.
一. 圆轴扭转时横截面上的应力
实验观察:
Me
γ φ
n
m
l
Me
nபைடு நூலகம்
m
mn没变 r没变 假设: 刚性 推理:外 里
n
n
R a b a b d O
dx
m
m
76 2 ( 76 2 2 . 5 ) 2 0 .3 3 4 2 46 . 9
显然,空心轴比实心轴节省材 料. 在扭转轴设计中,选用空心 轴是一种合理的设计.
W空 0 . 334 W实
§3.5 圆轴扭转时的 变形与刚度条件
一.两横截面间相对扭转角
材料力学第3章剪切与扭转

fcb 305N/mm2
满足承压条件,一个螺 栓所能承担的轴力值 Ncb d (t ) f cb
b Nv nv
d 2
4
f vb
Ncb d (t ) f cb
既满足抗剪,又满足承压,一个螺栓所能承 担的轴力 b b Nmin minNv , Ncb 已知总的轴向拉力(或压力)设计值N,连接 所需螺栓数为 N n b N min 收尾法取整
1.25
MPa
承压面 剪切面
400
400
80kN F
承压应力
Fbs F 80 103 8.33 MPa bs Abs Abs 60 160
例3-2
铆钉受力如图,承压应力计算有下列四种:
A. B. C. D. 解
bs=F/(td) bs=2F/(td) bs=2F/(td) bs=4F/(td)
连接件:螺栓、销钉、铆钉、键 木材的齿连接
剪切面个数nv
单面剪切 双面剪切 三面剪切 ……
F
F
F
F/2
F/2
F/2 F/2
F/3 F/3 F/3
3.1.2 杆件扭转变形的概念
外力特点
外力偶作用面垂直于杆件轴线,右手定则平行于杆件轴 线 外力偶矩平衡(静止不动,或匀角速度转动)
面或双面剪切
f v f vb
f ce f cb
单个螺栓抗剪 V N b f v A nv A 2 d b N nv Afv nv f vb 4 满足抗剪条件,一 个螺栓所能承担的 (钢板上)轴力值 2 d b Nv nv f vb 4
单个螺栓承压 Fbs N bs f cb Abs d t 同一受力方向 N d (t ) fcb 承压构件的较 小总厚度
剪切与轴扭转

4
4、扭转轴内最大剪应力
对于等截面轴,扭转 轴内最大剪应力发生 在扭矩最大的截面的 圆周上
d D
max
T max Wt
5、扭转强度条件
max
T max Wt
6、强度条件的应用
max
T max Wt
T max Wt
(1)校核强度
max
剪切力为Q
Q bl
P bl
单剪切与双剪切
单剪切
前面讨论的都是单剪切现象
P
P
双剪切
P/2 P/2
出现两个剪切面 剪切力为P 中间段 P/2 P/2 剪切面面 积2倍 剪切力为P/2 剪切面面 积单倍
左右两段
P P/2 P/2
P
结论:无论用中间段还是左右段分析,结果是一样的。
二、挤压
由上述实验推导出圆轴扭转的平面假设。
在圆周中取出一个楔 形体放大后见图(b)
根据几何关系,有
g
CC AC rd j dx
同理,距圆心为 处的切应变为:
dx 式中 d j dx 为扭转角沿轴的变化率,对给定的截面,其为常量。即 横截面上任意点的切应变与该点到圆心的距离成正比。
g
(2) 画扭矩图,求最大扭矩 用截面法求得AB.AC.CD各段的扭矩分别为:
T 1 T B 468 N m T 2 T A T B 1170 468 702 N m T 3 T A T B T C 1170 468 351 351 N m
F 为剪切内力,即剪应力在剪切面上的合力,我们称之为剪力
4、扭转轴内最大剪应力
对于等截面轴,扭转 轴内最大剪应力发生 在扭矩最大的截面的 圆周上
d D
max
T max Wt
5、扭转强度条件
max
T max Wt
6、强度条件的应用
max
T max Wt
T max Wt
(1)校核强度
max
剪切力为Q
Q bl
P bl
单剪切与双剪切
单剪切
前面讨论的都是单剪切现象
P
P
双剪切
P/2 P/2
出现两个剪切面 剪切力为P 中间段 P/2 P/2 剪切面面 积2倍 剪切力为P/2 剪切面面 积单倍
左右两段
P P/2 P/2
P
结论:无论用中间段还是左右段分析,结果是一样的。
二、挤压
由上述实验推导出圆轴扭转的平面假设。
在圆周中取出一个楔 形体放大后见图(b)
根据几何关系,有
g
CC AC rd j dx
同理,距圆心为 处的切应变为:
dx 式中 d j dx 为扭转角沿轴的变化率,对给定的截面,其为常量。即 横截面上任意点的切应变与该点到圆心的距离成正比。
g
(2) 画扭矩图,求最大扭矩 用截面法求得AB.AC.CD各段的扭矩分别为:
T 1 T B 468 N m T 2 T A T B 1170 468 702 N m T 3 T A T B T C 1170 468 351 351 N m
F 为剪切内力,即剪应力在剪切面上的合力,我们称之为剪力
第三章 扭转2资料重点
G
x 应变比能:
u
dU dV
dW dV
1 2
1 2
G
2
u
dU dV
dW dV
1 2
1 2
G
2
变形能: U dU 1dV
V
V2
V
1 2G
T
Ip
2
LdA
1 T 2 L 1 Me2 L
2G I p
2G I p
1 T L
G Ip
U GI p 2
2L
圆柱形密圈螺旋弹簧的计算 T
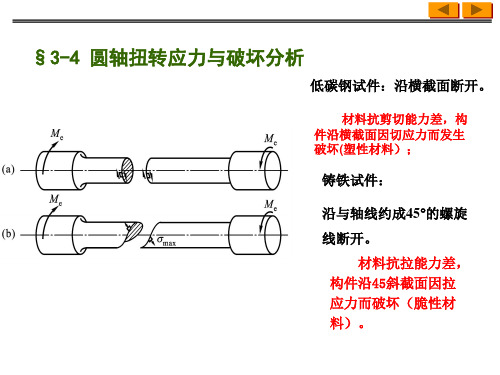
§3-4 圆轴扭转应力与破坏分析
低碳钢试件:沿横截面断开。
材料抗剪切能力差,构 件沿横截面因切应力而发生 破坏(塑性材料);
铸铁试件:
沿与轴线约成45的螺旋 线断开。
材料抗拉能力差, 构件沿45斜截面因拉 应力而破坏(脆性材 料)。
´ e
n
x 设:ef 边的面积为 dA 则
b ´f t
eb 边的面积为dAcosα ef 边的面积为dAsinα
Gd 4 64R3n
为 弹 簧 常 数.
max
K
8 DP
d3
64R3n P Gd 4
例 3 圆柱形密圈螺旋弹簧的平均直径为:D=125mm ,簧丝
直径为:d=18mm , 受拉力 P=500N 的作用,试求最大切
应力的近似值和精确值;若 G=82GPa ,欲使弹簧变形等于
6mm ,问:弹簧至少应有几圈?
4C 4 C
d
2、 簧丝的强度条件:
max
K
8DP
d 3
max
3、 弹簧位移的计算(能量法)
变性能
U dU 1 dV 1 (T )2 LdA
材料力学-第三章 扭转与剪切

力偶在单位时间内所做之功即功率P,等于该力偶之矩M与相应
角速度的乘积,即 P= M
P 103 M 2πn 60
M Nm
9549
PkW n r/min
2020/6/18
教材:材料力学(苏振超等主编)—南京大学出版社®
6
材料力学>>杆件的内力>>受扭杆件的内力>>
3.1.3 扭矩与扭矩图
2020/6/18
2020/6/18
教材:材料力学(苏振超等主编)—南京大学出版社®
41
材料力学>>扭转与剪切>>剪切与挤压的实用计算
例3-15 图示一广告牌由螺栓固定在立柱上。已知广告牌的自重为35kN,几 何尺寸如图所示(尺寸单位为mm),螺栓的直径为20mm, 试求螺栓剪 切面上的最大切应力值。
2020/6/18
29
材料力学>>扭转与剪切>>
3.4 圆轴扭转时的应变能
dW 0 dydz ddx
dVε
dW
dydz ddx ( d )dV
0
0
单位体积内的应变能(应变能密度)为
vε
dVε dV
d
0
vε
1
2
vε
2
2G
G
2
2
整个杆件的应变能: Vε V vεdV l A vεdAdx
2020/6/18
12
材料力学>>扭转与剪切>>圆轴的扭转应力
3.2.1 圆轴扭转的变形特点
作如下假设:在圆轴扭转变形过程中,横截面变形后仍保持为平 面,其形状和大小均不变,半径仍保持为直线,相邻两横截面间 的距离不变。这就是圆轴扭转的平面假设。
角速度的乘积,即 P= M
P 103 M 2πn 60
M Nm
9549
PkW n r/min
2020/6/18
教材:材料力学(苏振超等主编)—南京大学出版社®
6
材料力学>>杆件的内力>>受扭杆件的内力>>
3.1.3 扭矩与扭矩图
2020/6/18
2020/6/18
教材:材料力学(苏振超等主编)—南京大学出版社®
41
材料力学>>扭转与剪切>>剪切与挤压的实用计算
例3-15 图示一广告牌由螺栓固定在立柱上。已知广告牌的自重为35kN,几 何尺寸如图所示(尺寸单位为mm),螺栓的直径为20mm, 试求螺栓剪 切面上的最大切应力值。
2020/6/18
29
材料力学>>扭转与剪切>>
3.4 圆轴扭转时的应变能
dW 0 dydz ddx
dVε
dW
dydz ddx ( d )dV
0
0
单位体积内的应变能(应变能密度)为
vε
dVε dV
d
0
vε
1
2
vε
2
2G
G
2
2
整个杆件的应变能: Vε V vεdV l A vεdAdx
2020/6/18
12
材料力学>>扭转与剪切>>圆轴的扭转应力
3.2.1 圆轴扭转的变形特点
作如下假设:在圆轴扭转变形过程中,横截面变形后仍保持为平 面,其形状和大小均不变,半径仍保持为直线,相邻两横截面间 的距离不变。这就是圆轴扭转的平面假设。
《二三章剪切和扭转》课件
3 学习体会分享
4 疑问答疑
分享学员在学习过程中的体会和感悟,促进交流 和共同进步。
解答学员对剪切和扭转的理解和应用中遇到的问 题,提供更深入的解释和指导。
扭转运动的数学描述
扭转运动可以用转角和扭矩来描 述,转角是单位长度的旋转角度, 扭矩是单位长度上的扭转力矩。
扭转力的计算方法
扭转力的计算方法包括扭矩公式、 材料的剪切模量以及物体的几何 形状和材料性质等因素。
第三部分:练习
1
实际案例分析
通过实际案例分析剪切和扭转的应用,加剪切和扭转Fra bibliotek计算练习2
深对实际问题的理解和解决能力。
进行剪切和扭转的计算练习,巩固理论知
识,并培养解决实际问题的能力。
3
剪切和扭转的应用练习
通过练习应用剪切和扭转的知识,培养解 决实际问题的应用能力和创新思维。
第四部分:总结
1 课程回顾
2 知识点总结
对剪切和扭转的主要知识点进行回顾,巩固所学 内容。
总结剪切和扭转的物理原理、应用场景,以及数 学描述和计算方法。
第二部分:扭转
什么是扭转?
扭转是一种力沿垂直于物体表面 的方向作用于物体,使其绕垂直 轴线旋转的运动。
扭转的物理原理
扭转的物理原理涉及到扭矩和转 角之间的关系,影响扭转的因素 包括力的大小、材料的刚性和形 状。
扭转的应用场景
扭转应用广泛,如螺旋桨推进器、 发电机、捻线机等工业和日常生 活中的旋转设备。
剪切的应用场景
剪切广泛应用于工程、材料科 学、草地管理等领域,如金属 切削、剪切草坪。
剪切运动的数学描述
剪切运动可以用切变应变和切变应力来描述,切变 应变是单位长度的侧向位移,切变应力是单位面积 上的剪切力。
第三章剪切和扭转(pdf)
例题:如图所示连接件,盖板厚度t1=10mm,主板厚 度t2=20mm,板宽b=150mm,螺栓直径d=27mm。螺 栓的容许切应力[τ]=135MPa,钢板的容许挤压应力 [σbs]=305MPa,容许拉应力[σ]=170MPa。若 F=313kN,试校核该接头的强度。
b F t1 F t2 t1 F F
1
2
3
2、控制截面的扭矩
MeD
MeB 1 MeC
2
MeA
3
T1 = M eB = 0 . 48 kNm
T 2 = M eB + M eB
T/kNm 0.48
0.96
= 0 .96 kNm
T 3 = − M eD
0.64 x
= − 0 .64 kNm
3、扭矩图
思考题:若将主动轮A和从动轮D互换位置,轴上 的扭矩图是否有变化?变化后的放置方式是否合 理?
例题:圆轴受力如图所示,试作轴的扭矩图。 解: 1、确定控制面的扭矩 设正法
T 1 = 20 kNm
T 2 = 20 − 27 = − 7 kNm
1 27kNm 2
8kNm 3
3 15kNm
1 20kNm
2
T1 20kNm 27kNm T2 20kNm T3 15kNm
T 3 = − 15 kNm
(
)
16 × 2 × 10 6 = = 26.69 MPa 4 ⎡ ⎛ 95 ⎞ ⎤ 3 3.14 × 105 × ⎢1 − ⎜ ⎟ ⎥ ⎢ ⎝ 105 ⎠ ⎥ ⎣ ⎦
τ min
Tρ min 16Td = = Ip πD 4 1 − α 4
(
)
16 × 2 × 10 6 × 95 = = 24.14 MPa 4 ⎡ ⎛ 95 ⎞ ⎤ 4 3.14 × 105 × ⎢1 − ⎜ ⎟ ⎥ ⎢ ⎝ 105 ⎠ ⎥ ⎣ ⎦
材料力学剪切与扭转PPT课件
32
第32页/共97页
4 扭矩图
扭矩沿轴线方向变化的图形称为扭矩图。
T Me1
+
Me4
x
–
Me1+ Me2
扭矩图的X横坐标轴平行于杆件轴线,表示轴相应的横截面位置;纵坐 标表示该横截面的扭矩值。正扭矩画在X轴上方,负扭矩画在X轴下方。
扭矩图中需标明(+)、(-)以表示扭矩的正负。
33
第33页/共97页
2 FS
bs
F Abs
F lh 2
57 103 100 6106
95.3MPa bs
综上,键满足强度要求.
21
第21页/共97页
§3.2 扭转的概念和工程实例
一、扭转变形特点及基本概念 1. 扭转变形:是杆件的一种基本变形形式。在垂直于杆件轴线的平面内有力
偶作用时,各横截面将绕杆轴线作相对转动,杆件便产生扭转变形。
3、挤压的实用计算
挤压:构件局部面积的承压现象。 挤压力:在接触面上的压力,记FC
(1) 挤压力―FC F
(合力) F n
假设:挤压应力在有效挤压面上均匀分布。
第10页/共97页
F
F (合力)
10
(2)有效挤压面积Abs:实际挤压面在垂直于挤压力FC 方向的平面上的投影面积。
(3)挤压强度条件(准则) 工作挤压应力不得超过材料的许用挤压
在连接件与拉板接触 F处因挤压产生变形。
6
第6页/共97页
(合力) F n
F (合力)
FS
剪切面
n
n
F
4、连接处(接头)破坏三种形式 ①剪切破坏 沿螺栓的剪切面剪断,如 沿n– n面剪
断。 ②挤压破坏 螺栓与拉板在相互接触面上因挤压发生过
第32页/共97页
4 扭矩图
扭矩沿轴线方向变化的图形称为扭矩图。
T Me1
+
Me4
x
–
Me1+ Me2
扭矩图的X横坐标轴平行于杆件轴线,表示轴相应的横截面位置;纵坐 标表示该横截面的扭矩值。正扭矩画在X轴上方,负扭矩画在X轴下方。
扭矩图中需标明(+)、(-)以表示扭矩的正负。
33
第33页/共97页
2 FS
bs
F Abs
F lh 2
57 103 100 6106
95.3MPa bs
综上,键满足强度要求.
21
第21页/共97页
§3.2 扭转的概念和工程实例
一、扭转变形特点及基本概念 1. 扭转变形:是杆件的一种基本变形形式。在垂直于杆件轴线的平面内有力
偶作用时,各横截面将绕杆轴线作相对转动,杆件便产生扭转变形。
3、挤压的实用计算
挤压:构件局部面积的承压现象。 挤压力:在接触面上的压力,记FC
(1) 挤压力―FC F
(合力) F n
假设:挤压应力在有效挤压面上均匀分布。
第10页/共97页
F
F (合力)
10
(2)有效挤压面积Abs:实际挤压面在垂直于挤压力FC 方向的平面上的投影面积。
(3)挤压强度条件(准则) 工作挤压应力不得超过材料的许用挤压
在连接件与拉板接触 F处因挤压产生变形。
6
第6页/共97页
(合力) F n
F (合力)
FS
剪切面
n
n
F
4、连接处(接头)破坏三种形式 ①剪切破坏 沿螺栓的剪切面剪断,如 沿n– n面剪
断。 ②挤压破坏 螺栓与拉板在相互接触面上因挤压发生过
材料力学 剪切和扭转.
d
挤压面
P
P
解:Fs F jy F
剪切面
dh 2 2 挤压面面积: Abs ( D d ) 4 Fs P 挤压面 As dh
剪切面面积: As
d
50 103 66.3MPa 20 12
P
bs
Pbs 4P 4 50 103 102MPa bs 2 2 2 2 Abs ( D d ) (32 20 )
n
n
P (合力)
何平面)的平行力系作用。
②变形特点: 构件沿两组平行力系的交界面 发生相对错动。
(合力) P
③剪切面: 构件将发生相互的错动面,如
n
n
P (合力)
n– n 。
④剪切面上的内力: 内力 — 剪力FS ,其作用线与
FS
剪切面 剪切面平行。
n
P
n
⑤ 剪切面上的切应力: 与剪力FS 对应的应力称为切 应力
,产生剪切变形。
3、切应力互等定理:
(合力)
P
a
dy
´
dx
´
b
ห้องสมุดไป่ตู้
n
c z
d t
m
z
(合力) P n
0; t dxdy t dxdy
'
这就是切应力互等定理:在单元体相互垂直的两个截面 上,切应力必然成对出现,且数值相等,两者都垂直于两平 面的交线,其方向或共同指向交线,或共同背离交线。
n
n
P (合力) 剪切面 n
沿铆钉的剪切面剪断,如
沿n– n面剪断 。 ②挤压破坏 铆钉与钢板在相互接触面 上因挤压而使溃压连接松动,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
14
一、变形几何关系
取微段(长为dx); 在微段中取单元体abcd ; 截面nn相对截面mm的扭转角为 dϕ 半径线由Oa→ Oa' ; 单元体abcd的ab边相对于cd边产生了微小 的相对错动,引起了单元体abcd的剪切变 形;相对错动的长度为:
m
n
ϕ
m dx n m n
ρmax
aa ' = ρ max dϕ
ρτ ρ dA
M n = ∫ ρτ ρ dA
A
17
M n = ∫ ρ ⋅ τ ρ dA = ∫ ρ ⋅ G ρ
A A
dϕ dϕ dA = G ρ 2dA dx dx ∫A
dϕ M n = dx GI ρ
ρ max
dρ
令 I ρ = ∫ ρ 2 dA
A
dϕ M n = GI ρ dx
ρ τρ
dϕ (当在某一给定截面积分时, dx 为常量)
8
受力特点:在杆件两端作用两个大小相等、方向相反,且垂直于杆 件轴线的力偶;致使杆件的任意两个横截面产生绕杆件轴线的相对 转动。这种变形称扭转变形。 以扭转变形为主要变形的构件称为轴。 变形量用扭转角ϕ表示。
T
T
ϕ
A
B
9
§3.2.2 扭矩和扭矩图 一、 外力偶矩(转矩)的计算
已知:传递功率 P (kW)、轴的转速n (r/min) 求:外力偶矩Me Me: N·m
2
§3.1 剪切与挤压
§3.1.1 剪切与剪切强度的计算 一、剪切的概念
图3-1 螺栓受力情况
受力特点:构件受到大小相等、方向相反且作用线相距很近的一对力作用 变形特点:横截面发生相对错动,即剪切变形。 剪切面:发生相对错动的平面 剪力:剪切面上的内力Q 切应力:剪切面上剪力的分布集度,用τ表示。
Me
规定:用右手螺旋法则: 指出截面外: + 指向截面内: Me
A
T n n T n
Me
B
12
[例1]一等圆截面传动轴如图所示,其转速n=300 r/min,主动轮A的输入 功率PA=221 kW,从动轮B、C的输出功率分别为PB =148kW、PC =73kW。试 求轴上各截面的扭矩,并画出扭矩图。 解:(1) 计算外力偶矩
P = MeΒιβλιοθήκη ⋅ωPω: rad/s
P: W
M e = 1000 = 1000 P 1000 × 30 P P = ⋅ = 9550 ( N ⋅ m ) πn n n π 30 P = 9.55 × 106 × ( N ⋅ mm ) n
ω
Me转向:主动轮的P入产生的Me与轴的转向一致,从动轮P出所产 生的Me与轴的转向相反。
第3章 剪切与圆轴扭转
§3.1 剪切与挤压 §3.2 圆轴扭转 §3.3 圆轴扭转时的应力与强度条件 §3.4 圆轴扭转时的变形与刚度条件
1
第3章 剪切与圆轴扭转
重点:
剪切与挤压强度的实用计算 外力偶和扭矩的计算及扭矩图的绘制 圆轴扭转时的应力、强度条件、刚度条件
难点:
扭矩图的绘制 强度条件和刚度条件的应用
T1 = M C = 2324 ( N ⋅ m) T2 = − M B = −4711 ( N ⋅ m)
MC
MB
MC T
T1
T2
MB
2324 N ⋅ m
+ o
-
(3) 画扭矩图
x
4711N ⋅ m
13
§3.3 圆轴扭转时的应力与强度条件 §3.3.1 圆轴扭转时横截面上的应力
圆轴扭转的基本假设: 圆轴扭转前的横截面变形后仍保持为平面,形状和大小不变,且 相邻两截面间的距离不变,只是绕轴线相对转过了一个角度。 推论:圆轴扭转时横截面上只有垂直于半径方向的剪应力,而没 有正应力。
不满足挤压强度 根据挤压强度重新确定键的长度
Fp σp = = ≤ ⎡σ p ⎤ Ap l h ⎣ ⎦ 2 2Fp 2 ×17.5 ×103 = = 54.7 (mm ) l≥ 8 × 80 h ⎡σ p ⎤ ⎣ ⎦
根据键长系列选 l=55mm
7
Fp
§3.2 圆轴扭转
§3.2.1 扭转的概念 实例一 汽车方向盘的转向轴 实例二 汽车传动轴 实例三 丝锥
4
⎤ ⎥ ⎥ ⎦
=
WT2 =
πD 3
16
D2 = 53.1 mm
(3) 计算空心轴与实心轴重量之比
π
A1 = A2
(D 4
π
4
2 1
− d12 )
2 D2
902 − 852 = = 0.31 2 53.1
20
§3.4 圆轴扭转时的变形与刚度条件 §3.4.1 圆轴的扭转变形
dϕ M n = dx GI p dϕ = Mn dx GI p
10
二、扭矩和扭矩图 内力偶矩 T —— 扭矩
Me
T A n n T n T B
Me
x
∑M
x
= 0:
T = Me
规定:用右手螺旋法则: 指出截面外: + 指向截面内: -
Me
A T T
n n
T
Me
n
B
11
二、扭矩和扭矩图 内力偶矩 T —— 扭矩
平面图表示方法
n
∑M
x
= 0:
T = Me
Me
A n n B
角度改变量,即剪应变γ
d
a γ c
O
a ' dϕ b b'
n
15
γ = tan γ =
aa ' ρ max dϕ dϕ = = ρ max ad dx dx
m
一、变形几何关系
m
dϕ γ = ρ max dx
n
ρmax
ρ
距离圆心为ρ处的剪应变为: dϕ γρ = ρ
dx
ρ
d
c
a γ
O
a ' dϕ b b'
24
α = d D (空心截面)
18
四、圆轴扭转时的强度条件
τ max =
M n max WT ≤ [τ ]
[ 例 1] 汽 车 传 动 轴 由 45 号 钢 无 缝 钢 管 制 成 , 外 径 D = 90mm , 壁 厚 t=2.5mm,[τ]=60MPa,其所承受的最大外力偶矩为1.5kN·m,试校核其 强度。若在τmax 不变的条件下改用实心轴,试确定圆轴的直径D,并计 算空心轴与实心轴的重量比。 解: (1) 校核空心轴的扭转强度
解: 1.分析受力情况 以轴(包括平键)为研究对象,受力如图所示, 根据平衡条件可得 d ∑ mO (F ) = 0 : T −F 2 = 0 2T 2 × 35 × 103 = = 17.5 × 103 ( N ) F= 40 d 2.校核键的剪切强度
Q = F = 17.5 × 103 ( N )
3
二、剪切强度的计算
FQ
Fp
剪
力
FQ = Fp
剪切强度条件: τ =
FQ AQ
≤ [τ ]
切应力
τ=
FQ AQ
AQ:剪切面积;τ:切应力(MPa); [τ]:材料的许用切应力(MPa)。
4
§3.1.2 挤压与挤压强度的计算 一、挤压的概念
挤压:在外力作用下,连接件与被连接 件在其接触面上发生的相互压紧现象。 挤压力:挤压面上的压力,用Fp表示。 挤压应力:挤压面上挤压力的分布集 度,用σp表示。
所以轴的扭转强度足够。
19
(2) 确定实心圆轴直径 根据实心轴与空心轴最大剪应力相等的条件
τ max
Mn Mn = = = 51.2( MPa ) 3 WT πD 16
因此,抗扭截面模量WT必须相等。
WT1 =
πD1 (1 − α 4 )
3
16
=
π × 903 ⎡
16
⎛ 90 − 2 × 2.5 ⎞ × ⎢1 − ⎜ ⎟ 90 ⎝ ⎠ ⎢ ⎣
MA
PA 221 = 9550 × = 7035( N ⋅ m) n 300 P 148 M B = 9550 B = 9550 × = 4711( N ⋅ m) n 300 P 73 M c = 9550 C = 9550 × = 2324( N ⋅ m) n 300 M A = 9550
(2) 计算扭矩
二、挤压强度的计算
挤压应力: σ p =
Fp Ap
Fp Ap
Fp
σp
挤压强度条件: σ = p
≤ ⎡σ p ⎤ ⎣ ⎦
Fp
5
[例1] 铸铁带轮用平键与轴联接,如图所示。传递的力偶矩T=350Nm,轴的 直径d=40mm,平键尺寸b×h=12×8,初步确定键长l=35mm,键的材料为 45号钢,许用剪切应力[τ]=60 MPa,许用挤压应力[σp]=100MPa,铸铁的 许用挤压应力[σp]=80MPa,试校核键联接的强度。
n
O
γρ
dϕ
m
结论:横截面上任意点的剪应变与该点到圆心距离成正比。
16
二、应力应变关系
dϕ γρ = ρ dx
ρ max
dρ
τ = Gγ
τ ρ = Gγ ρ = G ρ
dϕ dx
ρ
τρ
横截面上任意点的剪应力与该 点到圆心距离成正比
三、最大剪应力的计算
环形微面积 微力偶矩 内力偶矩
dA = 2πρ ⋅ d ρ
WT =
τ max =
π D3
16
(1 − α ) =
4
π × 903 ⎡
16
4 ⎛ 90 − 2 × 2.5 ⎞ ⎤ 2.93×10-5 (m3) × ⎢1 − ⎜ ⎟ ⎥= 90 ⎠ ⎥ ⎢ ⎝ ⎣ ⎦
一、变形几何关系
取微段(长为dx); 在微段中取单元体abcd ; 截面nn相对截面mm的扭转角为 dϕ 半径线由Oa→ Oa' ; 单元体abcd的ab边相对于cd边产生了微小 的相对错动,引起了单元体abcd的剪切变 形;相对错动的长度为:
m
n
ϕ
m dx n m n
ρmax
aa ' = ρ max dϕ
ρτ ρ dA
M n = ∫ ρτ ρ dA
A
17
M n = ∫ ρ ⋅ τ ρ dA = ∫ ρ ⋅ G ρ
A A
dϕ dϕ dA = G ρ 2dA dx dx ∫A
dϕ M n = dx GI ρ
ρ max
dρ
令 I ρ = ∫ ρ 2 dA
A
dϕ M n = GI ρ dx
ρ τρ
dϕ (当在某一给定截面积分时, dx 为常量)
8
受力特点:在杆件两端作用两个大小相等、方向相反,且垂直于杆 件轴线的力偶;致使杆件的任意两个横截面产生绕杆件轴线的相对 转动。这种变形称扭转变形。 以扭转变形为主要变形的构件称为轴。 变形量用扭转角ϕ表示。
T
T
ϕ
A
B
9
§3.2.2 扭矩和扭矩图 一、 外力偶矩(转矩)的计算
已知:传递功率 P (kW)、轴的转速n (r/min) 求:外力偶矩Me Me: N·m
2
§3.1 剪切与挤压
§3.1.1 剪切与剪切强度的计算 一、剪切的概念
图3-1 螺栓受力情况
受力特点:构件受到大小相等、方向相反且作用线相距很近的一对力作用 变形特点:横截面发生相对错动,即剪切变形。 剪切面:发生相对错动的平面 剪力:剪切面上的内力Q 切应力:剪切面上剪力的分布集度,用τ表示。
Me
规定:用右手螺旋法则: 指出截面外: + 指向截面内: Me
A
T n n T n
Me
B
12
[例1]一等圆截面传动轴如图所示,其转速n=300 r/min,主动轮A的输入 功率PA=221 kW,从动轮B、C的输出功率分别为PB =148kW、PC =73kW。试 求轴上各截面的扭矩,并画出扭矩图。 解:(1) 计算外力偶矩
P = MeΒιβλιοθήκη ⋅ωPω: rad/s
P: W
M e = 1000 = 1000 P 1000 × 30 P P = ⋅ = 9550 ( N ⋅ m ) πn n n π 30 P = 9.55 × 106 × ( N ⋅ mm ) n
ω
Me转向:主动轮的P入产生的Me与轴的转向一致,从动轮P出所产 生的Me与轴的转向相反。
第3章 剪切与圆轴扭转
§3.1 剪切与挤压 §3.2 圆轴扭转 §3.3 圆轴扭转时的应力与强度条件 §3.4 圆轴扭转时的变形与刚度条件
1
第3章 剪切与圆轴扭转
重点:
剪切与挤压强度的实用计算 外力偶和扭矩的计算及扭矩图的绘制 圆轴扭转时的应力、强度条件、刚度条件
难点:
扭矩图的绘制 强度条件和刚度条件的应用
T1 = M C = 2324 ( N ⋅ m) T2 = − M B = −4711 ( N ⋅ m)
MC
MB
MC T
T1
T2
MB
2324 N ⋅ m
+ o
-
(3) 画扭矩图
x
4711N ⋅ m
13
§3.3 圆轴扭转时的应力与强度条件 §3.3.1 圆轴扭转时横截面上的应力
圆轴扭转的基本假设: 圆轴扭转前的横截面变形后仍保持为平面,形状和大小不变,且 相邻两截面间的距离不变,只是绕轴线相对转过了一个角度。 推论:圆轴扭转时横截面上只有垂直于半径方向的剪应力,而没 有正应力。
不满足挤压强度 根据挤压强度重新确定键的长度
Fp σp = = ≤ ⎡σ p ⎤ Ap l h ⎣ ⎦ 2 2Fp 2 ×17.5 ×103 = = 54.7 (mm ) l≥ 8 × 80 h ⎡σ p ⎤ ⎣ ⎦
根据键长系列选 l=55mm
7
Fp
§3.2 圆轴扭转
§3.2.1 扭转的概念 实例一 汽车方向盘的转向轴 实例二 汽车传动轴 实例三 丝锥
4
⎤ ⎥ ⎥ ⎦
=
WT2 =
πD 3
16
D2 = 53.1 mm
(3) 计算空心轴与实心轴重量之比
π
A1 = A2
(D 4
π
4
2 1
− d12 )
2 D2
902 − 852 = = 0.31 2 53.1
20
§3.4 圆轴扭转时的变形与刚度条件 §3.4.1 圆轴的扭转变形
dϕ M n = dx GI p dϕ = Mn dx GI p
10
二、扭矩和扭矩图 内力偶矩 T —— 扭矩
Me
T A n n T n T B
Me
x
∑M
x
= 0:
T = Me
规定:用右手螺旋法则: 指出截面外: + 指向截面内: -
Me
A T T
n n
T
Me
n
B
11
二、扭矩和扭矩图 内力偶矩 T —— 扭矩
平面图表示方法
n
∑M
x
= 0:
T = Me
Me
A n n B
角度改变量,即剪应变γ
d
a γ c
O
a ' dϕ b b'
n
15
γ = tan γ =
aa ' ρ max dϕ dϕ = = ρ max ad dx dx
m
一、变形几何关系
m
dϕ γ = ρ max dx
n
ρmax
ρ
距离圆心为ρ处的剪应变为: dϕ γρ = ρ
dx
ρ
d
c
a γ
O
a ' dϕ b b'
24
α = d D (空心截面)
18
四、圆轴扭转时的强度条件
τ max =
M n max WT ≤ [τ ]
[ 例 1] 汽 车 传 动 轴 由 45 号 钢 无 缝 钢 管 制 成 , 外 径 D = 90mm , 壁 厚 t=2.5mm,[τ]=60MPa,其所承受的最大外力偶矩为1.5kN·m,试校核其 强度。若在τmax 不变的条件下改用实心轴,试确定圆轴的直径D,并计 算空心轴与实心轴的重量比。 解: (1) 校核空心轴的扭转强度
解: 1.分析受力情况 以轴(包括平键)为研究对象,受力如图所示, 根据平衡条件可得 d ∑ mO (F ) = 0 : T −F 2 = 0 2T 2 × 35 × 103 = = 17.5 × 103 ( N ) F= 40 d 2.校核键的剪切强度
Q = F = 17.5 × 103 ( N )
3
二、剪切强度的计算
FQ
Fp
剪
力
FQ = Fp
剪切强度条件: τ =
FQ AQ
≤ [τ ]
切应力
τ=
FQ AQ
AQ:剪切面积;τ:切应力(MPa); [τ]:材料的许用切应力(MPa)。
4
§3.1.2 挤压与挤压强度的计算 一、挤压的概念
挤压:在外力作用下,连接件与被连接 件在其接触面上发生的相互压紧现象。 挤压力:挤压面上的压力,用Fp表示。 挤压应力:挤压面上挤压力的分布集 度,用σp表示。
所以轴的扭转强度足够。
19
(2) 确定实心圆轴直径 根据实心轴与空心轴最大剪应力相等的条件
τ max
Mn Mn = = = 51.2( MPa ) 3 WT πD 16
因此,抗扭截面模量WT必须相等。
WT1 =
πD1 (1 − α 4 )
3
16
=
π × 903 ⎡
16
⎛ 90 − 2 × 2.5 ⎞ × ⎢1 − ⎜ ⎟ 90 ⎝ ⎠ ⎢ ⎣
MA
PA 221 = 9550 × = 7035( N ⋅ m) n 300 P 148 M B = 9550 B = 9550 × = 4711( N ⋅ m) n 300 P 73 M c = 9550 C = 9550 × = 2324( N ⋅ m) n 300 M A = 9550
(2) 计算扭矩
二、挤压强度的计算
挤压应力: σ p =
Fp Ap
Fp Ap
Fp
σp
挤压强度条件: σ = p
≤ ⎡σ p ⎤ ⎣ ⎦
Fp
5
[例1] 铸铁带轮用平键与轴联接,如图所示。传递的力偶矩T=350Nm,轴的 直径d=40mm,平键尺寸b×h=12×8,初步确定键长l=35mm,键的材料为 45号钢,许用剪切应力[τ]=60 MPa,许用挤压应力[σp]=100MPa,铸铁的 许用挤压应力[σp]=80MPa,试校核键联接的强度。
n
O
γρ
dϕ
m
结论:横截面上任意点的剪应变与该点到圆心距离成正比。
16
二、应力应变关系
dϕ γρ = ρ dx
ρ max
dρ
τ = Gγ
τ ρ = Gγ ρ = G ρ
dϕ dx
ρ
τρ
横截面上任意点的剪应力与该 点到圆心距离成正比
三、最大剪应力的计算
环形微面积 微力偶矩 内力偶矩
dA = 2πρ ⋅ d ρ
WT =
τ max =
π D3
16
(1 − α ) =
4
π × 903 ⎡
16
4 ⎛ 90 − 2 × 2.5 ⎞ ⎤ 2.93×10-5 (m3) × ⎢1 − ⎜ ⎟ ⎥= 90 ⎠ ⎥ ⎢ ⎝ ⎣ ⎦
