高一数学分数指数幂
n次方根与分数指数幂课件高一上学期数学人必修第一册

计算: (4^4)^(1/4)
计算: (5^5)^(1/5)
05
n次方根与分数指数幂的应用
n次方根在解决实际问题中的应用
计算器:利用n 次方根进行数值 计算
工程设计:利用 n次方根进行尺 寸和比例的计算
物理学:利用n 次方根进行能量 和功率的计算
化学:利用n次 方根进行浓度和 反应速率的计算
分数指数幂在解决实际问题中的应用
n次方根的运算性质
n次方根的定义:如果一个数x的n次方等于a,那么x就是a的n次方根。 n次方根的性质:n次方根具有封闭性、结合性和分配性。 封闭性:n次方根的结果是一个实数,且满足a^n=b^n,则a=b。 结合性:n次方根的结果可以参与四则运算,且满足a^(m+n)=a^ma^n。 分配性:n次方根的结果可以参与乘除运算,且满足a^(m/n)=a^m/a^n。
应用场景:解 方程、化简表 达式、求值域
等
示例:a^2 + b^2 = (a^2 + b^2)^(1/2)
= (a^2 + b^2)^(1/2)
注意事项:指 数为分数时, 底数不能为0, 否则公式不成
立
04
n次方根与分数指数幂的运算
n次方根与分数指数幂的运算顺序
先进行n次方根的运算,再计算 分数指数幂
遵循先算括号内,再算括号外 的原则
遵循先乘除,后加减的原则
遵循先算指数,再算底数的原 则
运算的优先级
如果有括号,先计算括号内 的运算
同级运算,从左到右进行计 算
先进行分数指数幂的运算, 再计算n次方根
如果有负指数幂,先计算负 指数幂的运算
运算的实例
计算: (2^2)^(1/3)
计算: (3^3)^(1/2)
4.1.1n次方根与分数指数幂课件高一上学期数学人教A版

思考 6►►► n an表示 an 的 n 次方根,n an=a 一定成立吗?如果不一定成立,那 么n an等于什么? 【解析】 不一定成立,当 n 为奇数时,n an=a; 当 n 为偶数时,n an=|a|=a-,a,a≥a0<,0.
内容索引
例 1 求下列各式的值:
(1) 3 -83; 【解析】 3 -83=-8. (2) -102;
第四章 指数函数与对数函数
4.1 指数 4.1.1 n次方根与分数指数幂
内容索引
学习目标 活动方案 检测反馈
内容索引
1. 了解n次方根的概念及其性质. 2. 了解根式的概念及其性质. 3. 理解分数指数幂的定义,把握分式与负整数指数幂、根式与正 分数指索引
此类问题的解答首先应去根号,这就要求将被开方部分化为完全平 方的形式,结合根式性质求解.
内容索引
例3中,若将“-3<x<3”变为“x≤-3”,则结果又是什么? 【解析】 原式= x-12- x+32=|x-1|-|x+3|. 因为 x≤-3,所以 x-1≤-4,x+3≤0, 所以原式=-(x-1)+(x+3)=4.
内容索引
活动五 分数指数幂
思考 7►►► 根据 n 次方根的定义和数的运算,我们知道
5 a10=5
10
a25=a2=a 5
(a>0),
4 a12=4
12
a34=a3=a 4
(a>0).
从以上式子中,你能总结出怎样的规律?
【解析】 这表明,当根式的被开方数(看成幂的形式)的指数能被根 指数整除时,根式可以表示为分数指数幂的形式.
【解析】 由于整数指数幂、分数指数幂都有意义,因此,有理数 指数幂是有意义的,整数指数幂的运算性质,可以推广到有理数指数幂, 即:
人教版高一数学必修1第16课时分数指数幂与幂的运算(含解析)
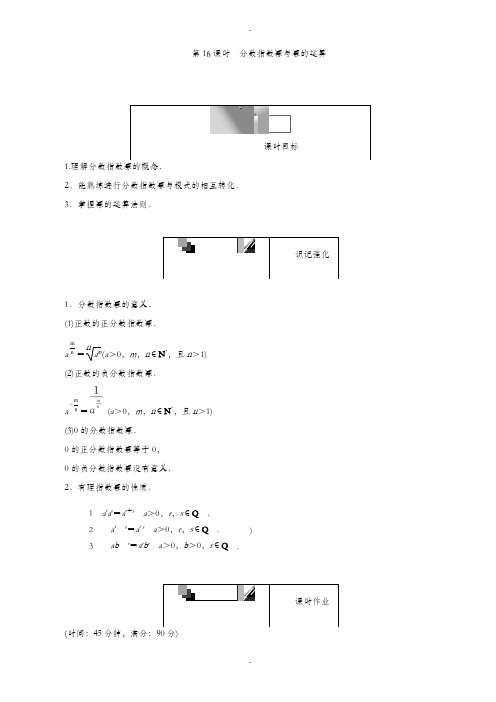
13.(15分)设 的整数部分为x,小数部分为y,求x2+ xy+ 的值.
解:因为 = = =2+ ,
所以x=2,y= .
原式=22+ ·2· + =4+7- + +1=12.
=2-4× +10(2+ )-10
=21.
(3)(7+4 ) -81 +32 -2× + × -1
=[(2+ )2] -(34) +(25) -2×(2-3) +2 ×(22)
=2+ - +8-8+2
=4.
11.(13分)已知x +x =3,计算:
(1)x-x-1;
(2) .
解:(1)将x +x =3两边平方,得x+x-1+2=32,即x+x-1=7,
0的正分数指数幂等于0,
0的负分数指数幂没有意义.
2.有理指数幂的性质.
课时作业
(时间:45分钟,满分:90分)
一、选择题(本大题共6小题,每小题5分,共30分)
1.把根式 改写成分数指数幂的形式为()
A.(a-b) B.(a-b)
C.a -b D.a -b
答案:A
解析:原式=[(a-b)-2] =(a-b) .故选A.
∵ =(x3+y3) ≠(x+y) ,∴C错;
∵ = =3 ,∴D正确,故选D.
4.式子 (a>0)经过计算可得()
A.aB.-
C. D.
答案:D
解析:原式= =a =a = .
5.设x,y,z∈R,xyz≠0,且4x=6y=144z,则()
A. = + B. = +
C. = + D. = +
答案:D
答案:1
解析:设ax=by=cz=k,则k>0,a=k ,b=k ,c=k ,因此abc=k k k =k =k0=1.
高一上学期数学人教A版必修第一册n次方根与分数指数幂

1
2
正方形场地的边长关于面积的函数= 记作= ,因此猜测,指数的范
围还能进一步拓展.
探究新知
问题3
初中阶段,我们由平方、立方的运算,引入了平方根、立方根.类比平方根、
立方根与平方、立方之间的关系,试着说说4次方根、5次方根……由此可以得出n
仍然适用,你能一一验证吗?
整数指数幂的运算性质对于有理数指数幂也同样适用,
即对于任意有理数r,s,均有下面的运算性质:
r s
r s
(1)a a a a 0,r,s Q ;
(2) a
r s
(3) ab
r
a rs a 0,r,s Q ;
a r b r a 0,b 0,r Q .
是说将指数的范围从整数拓展到有
理数后,其运算性质保持不变.其
形式上就是幂之间的运算转化为指
数间的运算,这一转化是以降低一
个运算级来实现的.
归纳总结
问题7
(1)本节课研究了哪些内容?怎样研究的?有理数指数幂运算性质有什么特点?
(2)通过本节课的学习,你认为指数幂运算的体系完善了吗?为什么?
(2)还没有完善,还需要研究无理数指数幂.
答案:
因为任何实数的偶次方幂都是非负数,所以在实数范围内,负数没有偶次方根.
探究新知
问题3
追问2 观察所举的例子,当n为偶数时,被开方数的符号、n次方根分别是什么?当
n为奇数时呢?
答案:
当为偶数时,被开方数是非负数,正数的次方根有两个,且互为相反数.
• 这时,正数的正的次方根用 表示,负的次方根用− 表示.
n次方根与分数指数幂课件-高一数学人教A版(2019)必修第一册

根式的概念
式子
n
a
叫做根式,这里n叫做根指数,a叫做被开方数。
根式
根指数
n
被开方数
a
根式的性质:
1. 1)
2 2
4
4
5
2)
-6
5
6
0 0
4
4
3)
4)
6 6
5
5
( a) a
n
2. 1)
4
2
4
2
4
2)
n
n
(2) 2 3)
4
5
(6)
a, n为奇数
, ≥ -,
(3)
-, < -
【变式训练 1】 (1) (-) =
;
(2)使等式 (-)( -)=(3-a) + 成立的实数 a 的取值范
围是
.
解析:(1) (-) =-2;
(2)因为 (-)( -) =
(-) ( + )=|a-3|· + =(3-a) + ,
无理数指数幂
4.将下列根式与分数指数幂进行互化.
3 2
(1)a · a ;(2)
3
答案 1a
2
3
-4
2
a b
3
ab2(a>0,b>0).
2
3
• 3 a 2 a3 • a a
3
2
3
a ,
a 4b 2 • 3 ab 2 a 4b 2 • ab
11
3
1
2 3
1
3
a
高一上学期数学人教A版必修第一册4.1.1n次方根与分数指数幂课件

第四章 指数函数与对数函数 4.1.1 n次方根与分数指数幂
2024/11/8
学习目标
学科素养
1. 理解并掌握根式、分数指数幂的概念; 2. 理解根式与分数指数幂的互化; 3. 掌握有理数指数幂的运算性质; 4. 培养勇于探索的精神,体会由特殊到一般的研究方 法,发展数学核心素养.
定义2:式子n a 叫做根式,n叫做根指数,a叫做
被开方数
(n>1,且nN*)
1(. 1)( 3 8)3 8 (2) ( 5 32)5 =-32 (3) (4 16)4 16
当n为任意正整数时,( n a )n=a.
(n>1,且nN*)
1(. 1)( 3 8)3 8 (2) ( 5 32)5 =-32 (3) (4 16)4 16
(2)
(3) 4 (3 )4
(4)
解:(1) 3 ( 8)3 8
(2) ( 10)2 | 10 | 10
( 10)2 (a b)2 (a b)
(3) 4 (3 )4 | 3 | 3
(4) (a b)2 | a b | a b
同类训练
举一反三
1. (a b)2 + 5 (a b)5的值是( ) 再细想!
类似地,(±2)4=16,则±2叫做16的 4次方根 ; 25=32,则2叫做32的 5次方根 .
2n = a,则2叫a做的__n_次__方__根___
xn =a 则x叫做a的_n__次__方__根___
.
类比分析 可是个好方法!
定义1:如果xn=a(n>1,且nN*),则称x是a的n次方根.
一个数的n次方根有几个?
3 3 27
2 3 8
22 4 3 2 9
高一数学上册 指数函数知识点及练习题含答案
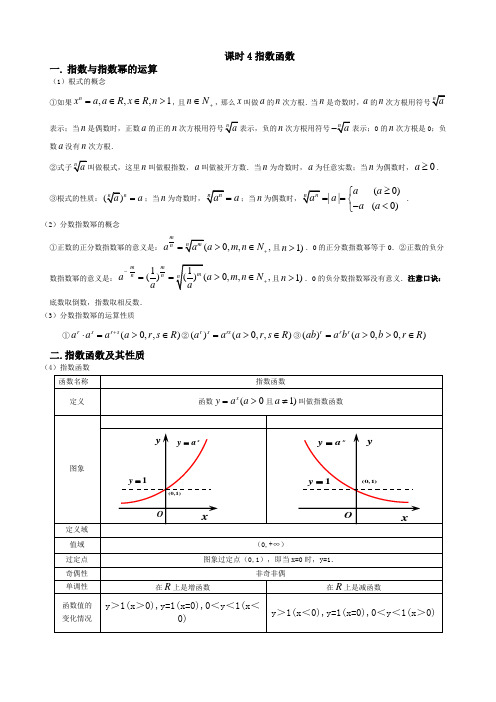
课时4指数函数一. 指数与指数幂的运算(1)根式的概念 ①如果,,,1nxa a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n表示;当n 是偶数时,正数a 的正的nn次方根用符号0的n 次方根是0;负数a 没有n 次方根.n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥.③根式的性质:n a =;当na =;当n(0)|| (0)a a a a a ≥⎧==⎨-<⎩.(2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,m naa m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是: 1()0,,,m m nn aa m n N a -+==>∈且1)n >.0的负分数指数幂没有意义.注意口诀:底数取倒数,指数取相反数. (3)分数指数幂的运算性质①(0,,)rs r s aa a a r s R +⋅=>∈②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r r ab a b a b r R =>>∈二.指数函数及其性质(4)指数函数a 变化对图象影响在第一象限内,a 越大图象越高,越靠近y 轴; 在第二象限内,a 越大图象越低,越靠近x 轴. 在第一象限内,a 越小图象越高,越靠近y 轴; 在第二象限内,a 越小图象越低,越靠近x 轴.三.例题分析1.设a 、b 满足0<a<b<1,下列不等式中正确的是(C) A.a a <a b B.b a <b b C.a a <b a D.b b <a b解析:A 、B 不符合底数在(0,1)之间的单调性;C 、D 指数相同,底小值小.故选C. 2.若0<a<1,则函数y=a x 与y=(a-1)x 2的图象可能是(D)解析:当0<a<1时,y=a x为减函数,a-1<0,所以y=(a-1)x 2开口向下,故选D.3.设指数函数f(x)=a x (a>0且a ≠1),则下列等式中不正确的是(D) A.f(x+y)=f(x)f(y)B.f(x-y)=)()(y f x f C.f(nx)=[f(x)]n D.f [(xy)n ]=[f(x)]n [f(y)]n (n ∈N *) 解析:易知A 、B 、C 都正确. 对于D,f [(xy)n]=a(xy)n,而[f(x)]n·[f(y)]n=(a x )n·(a y)n=anx+ny,一般情况下D 不成立.4.设a=31)43(-,b=41)34(-,c=43)23(-,则a 、b 、c 的大小关系是(B)A.c<a<bB.c<b<aC.b<a<cD.b<c<a解析:a=413131)34()34()43(>=-=b,b=434141)23()278()34(-=>=c.∴a>b>c.5.设f(x)=4x -2x+1,则f -1(0)=______1____________. 解析:令f -1(0)=a,则f(a)=0即有4a-2·2a=0.2a·(2a-2)=0,而2a>0,∴2a=2得a=1.6.函数y=a x-3+4(a>0且a ≠1)的反函数的图象恒过定点______(5,3)____________.解析:因y=a x的图象恒过定点(0,1),向右平移3个单位,向上平移4个单位得到y=a x-3+4的图象,易知恒过定点(3,5).故其反函数过定点(5,3).7.已知函数f(x)=xx xx --+-10101010.证明f(x)在R 上是增函数.证明:∵f(x)=1101101010101022+-=+---x x xx x x , 设x 1<x 2∈R ,则f(x 1)-f(x 2)=)110)(110()1010(21101101101101010101010101010212122112222111122222222++-=+--+-=+--+-----x x x x x x x x x x x x x x x x . ∵y=10x 是增函数, ∴21221010x x -<0. 而1210x +1>0,2210x +1>0, 故当x 1<x 2时,f(x 1)-f(x 2)<0, 即f(x 1)<f(x 2). 所以f(x)是增函数.8.若定义运算a ⊗b=⎩⎨⎧<≥,,,,b a a b a b 则函数f(x)=3x ⊗3-x 的值域为(A)A.(0,1]B.[1,+∞)C.(0,+∞)D.(-∞,+∞)解析:当3x ≥3-x ,即x ≥0时,f(x)=3-x ∈(0,1];当3x<3-x,即x<0时,f(x)=3x∈(0,1).∴f(x)=⎩⎨⎧<≥-,0,3,0,3x x x x 值域为(0,1).9.函数y=a x 与y=-a -x (a>0,a ≠1)的图象(C) A.关于x 轴对称B.关于y 轴对称 C.关于原点对称D.关于直线y=-x 对称解析:可利用函数图象的对称性来判断两图象的关系.10.当x ∈[-1,1]时,函数f(x)=3x -2的值域为_______[-35,1]___________. 解析:f(x)在[-1,1]上单调递增.11.设有两个命题:(1)关于x 的不等式x 2+2ax+4>0对一切x ∈R 恒成立;(2)函数f(x)=-(5-2a)x 是减函数.若命题(1)和(2)中有且仅有一个是真命题,则实数a 的取值范围是_______(-∞,-2)__________.解析:(1)为真命题⇔Δ=(2a)2-16<0⇔-2<a<2.(2)为真命题⇔5-2a>1⇔a<2.若(1)假(2)真,则a ∈(-∞,-2].若(1)真(2)假,则a ∈(-2,2)∩[2,+∞]=∅. 故a 的取值范围为(-∞,-2).12.求函数y=4-x -2-x +1,x ∈[-3,2]的最大值和最小值. 解:设2-x =t,由x ∈[-3,2]得t ∈[41,8],于是y=t 2-t+1=(t-21)2+43.当t=21时,y 有最小值43.这时x=1.当t=8时,y 有最大值57.这时x=-3. 13.已知关于x 的方程2a 2x-2-7a x-1+3=0有一个根是2,求a 的值和方程其余的根. 解:∵2是方程2a 2x-2-9a x-1+4=0的根,将x=2代入方程解得a=21或a=4. (1)当a=21时,原方程化为2·(21)2x-2-9(21)x-1+4=0.① 令y=(21)x-1,方程①变为2y 2-9y+4=0, 解得y 1=4,y 2=21.∴(21)x-1=4⇒x=-1,(21)x-1=21⇒x=2. (2)当a=4时,原方程化为2·42x-2-9·4x-1+4=0.② 令t=4x-1,则方程②变为2t 2-9t+4=0.解得t 1=4,t 2=21. ∴4x-1=4⇒x=2, 4x-1=21⇒x=-21. 故方程另外两根是当a=21时,x=-1; 当a=4时,x=-21. 14.函数y=243)31(x x -+-的单调递增区间是(D) A.[1,2]B.[2,3]C.(-∞,2]D.[2,+∞)解析:因为y=3x2-4x+3,又y=3t 单调递增,t=x 2-4x+3在x∈[2,+∞)上递增,故所求的递增区间为[2,+∞).15.已知f(x)=3x-b (2≤x ≤4,b 为常数)的图象经过点(2,1),则F(x)=f 2(x)-2f(x)的值域为(B) A.[-1,+∞)B.[-1,63) C.[0,+∞)D.(0,63]解析:由f(2)=1,得32-b =1,b=2,f(x)=3x-2. ∴F(x)=[f(x)-1]2-1=(3x-2-1)2-1. 令t=3x-2,2≤x≤4.∴g(t)=(t -1)2-1,t∈[1,9]. ∴所求值域为[-1,63].2.1指数函数练习1.下列各式中成立的一项()A .7177)(m n mn= B .31243)3(-=-C .43433)(y x y x +=+D .3339=2.化简)31()3)((656131212132b a b a b a ÷-的结果()A .a 6B .a -C .a 9-D .29a3.设指数函数)1,0()(≠>=a a a x f x ,则下列等式中不正确的是() A .f (x +y )=f(x )·f (y ) B .)()(y f x f y x f =-)( C .)()]([)(Q n x f nx f n∈=D .)()]([·)]([)(+∈=N n y f x f xy f n n n4.函数21)2()5(--+-=x x y()A .}2,5|{≠≠x x xB .}2|{>x xC .}5|{>x xD .}552|{><<x x x 或5.若指数函数x a y =在[-1,1]上的最大值与最小值的差是1,则底数a 等于 ()A .251+B .251+- C .251± D .215± 6.当a ≠0时,函数y ax b =+和y b ax =的图象只可能是 ()7.函数||2)(x x f -=的值域是()A .]1,0(B .)1,0(C .),0(+∞D .R8.函数⎪⎩⎪⎨⎧>≤-=-0,0,12)(21x x x x f x ,满足1)(>x f 的x 的取值范围 ()A .)1,1(-B .),1(+∞-C .}20|{-<>x x x 或D .}11|{-<>x x x 或9.函数22)21(++-=x x y 得单调递增区间是 ()A .]21,1[-B .]1,(--∞C .),2[+∞D .]2,21[10.已知2)(xx e e x f --=,则下列正确的是 ()A .奇函数,在R 上为增函数B .偶函数,在R 上为增函数C .奇函数,在R 上为减函数D .偶函数,在R 上为减函数 11.已知函数f (x )的定义域是(1,2),则函数)2(x f 的定义域是. 12.当a >0且a ≠1时,函数f (x )=a x -2-3必过定点. 三、解答题:13.求函数y x x =--1511的定义域.14.若a >0,b >0,且a +b =c ,求证:(1)当r >1时,a r +b r <c r ;(2)当r <1时,a r +b r >c r .15.已知函数11)(+-=x x a a x f (a >1).(1)判断函数f (x )的奇偶性;(2)证明f (x )在(-∞,+∞)上是增函数.16.函数f(x)=a x(a>0,且a ≠1)在区间[1,2]上的最大值比最小值大,求a 的值.参考答案一、DCDDDAADDA二、11.(0,1);12.(2,-2); 三、13.解:要使函数有意义必须:∴定义域为:{}x x R x x ∈≠≠且01,14.解:rrrrr c b c a c b a ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+,其中10,10<<<<cbc a . 当r >1时,1=+<⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr,所以a r +b r <c r; 当r <1时,1=+>⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr ,所以a r +b r >c r . 15.解:(1)是奇函数.(2)设x 1<x 2,则1111)()(221121+--+-=-x x x x a a a a x f x f 。
高一数学分数指数幂数学教案

高一数学分数指数幂数学教案一、教学目标1.理解分数指数幂的定义。
2.学会运用分数指数幂的性质进行计算。
3.能够运用分数指数幂的知识解决实际问题。
二、教学重难点重点:分数指数幂的定义及性质。
难点:分数指数幂的计算及实际应用。
三、教学过程1.导入新课(1)复习整数指数幂的概念和性质。
(2)引导学生思考:当指数为分数时,幂的运算规律会发生怎样的变化?2.新课讲解(1)分数指数幂的定义引导学生回顾整数指数幂的定义,然后类比得出分数指数幂的定义。
板书:a^(m/n)=(a^m)^(1/n)=(a^(1/n))^m(2)分数指数幂的性质引导学生通过举例验证分数指数幂的性质。
板书:a^(m/n)a^(p/q)=a^((m/n)+(p/q))(a^m)^n=a^(mn)(a^m)^(1/n)=a^(m/n)(a^m)^(p/q)=a^((mp)/(nq))(3)分数指数幂的运算讲解分数指数幂的运算方法,引导学生运用分数指数幂的性质进行计算。
例题:计算(2^3)^(1/2)(2^2)^(3/4)解析:根据分数指数幂的性质,我们可以将原式化简为2^(3/2)2^(3/2)=2^(3+3/2)=2^(9/2)3.练习与巩固(1)课堂练习1.计算(3^4)^(1/2)(3^2)^(3/4)2.计算(5^3)^(2/3)/(5^2)^(1/3)(2)课后作业1.计算(2^5)^(1/2)(2^3)^(1/4)2.计算(7^2)^(3/2)/(7^3)^(1/2)3.已知a>0,求证:(a^(m/n))^(p/q)=a^((mp)/(nq))4.课堂小结5.课后反思教师根据课堂教学情况,反思教学效果,为下节课的教学做好准备。
四、教学反思本节课通过复习整数指数幂的概念和性质,引导学生类比得出分数指数幂的定义和性质。
在教学过程中,注重让学生通过举例验证分数指数幂的性质,培养学生的动手操作能力和思维能力。
在练习环节,让学生独立完成课堂练习和课后作业,巩固所学知识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x2 )(x 1 x1) 2
x2 x2 3
x2 x2 3
3(x x1 1) 2 x2 x2 3
①
1
1
∵x 2 x2 =3,
两边平方得x+x 1 =7,再平方得x 2 +x 2 =47.代入①式 原式= 3(3 1) 2 = 2 .
47 3 5
阅读分数指数幂,回答以下问题: (1)分数指数幂是如何定义的; (2)有理指数幂的运算性质是怎样的;
a > 0,m、n∈N *,n > 1
正数的正分数指数幂的意义:
m
a n n am
正数的负分数指数幂的意义:
m
a n
1
m
an
0 的正分数指数幂等于 0 ; 0 的负分数指数幂没有意义
有理指数幂的运算性质: ( a> 0,b > 0,r、 s∈ Q ) (1)a r×a s = a r + s (2)( a r ) s = a rs (3)( ab ) r = a r×b r
口答:
1、用根式表示下列各式: ( a > 0 )
1
( 1 ) a5
3
( 2 ) a4
3
(3) a 5
5a
4 a3
1
5 a3
2、用分数指数幂表示下列各式:
2
(4) a 3
1 3 a2
( 1 ) 4 (a b)3 (a b 0) ( 2 ) 3 (m n)2 (m n)
3
(a b)4
2
(m n)3
( 3 ) (m n)4 (m n) ( 4 ) p6 q5 ( p 0, q 0)
(m n)2
5
p3 q2
例1:求下列各式的值。
1
(1)1002 =10
2
(2)83 =4
3
(3)9 2
1 27
(4)(
1) 81
3 4
=27
3
6
(5)2 3 1.5 12 =6
1
2
3
1
(6)[(0.0273 )2.5 ]5 [2560.125 (32)5 0.11]2
13
(2)(a 3 a 4 )12
2 1
(3)4a 3b 3
(
2
1 1
a 3b 3 )
3
1
1
1
1
(4)(2a 2 3b 4 )(2a 2 3b 4 )
(5)(a2 2 a2 ) (a2 a2 )
1
例4:已知x2
+x-
1 2
3
求
3
x2
x2
+x-
3 2
+x-2
2 3
的值。
1
1
1
1
解
原式= (x 2 )3
(1)分数指数幂的定义和运算性质 (2)有理数指数幂的定义和运算性质 (3)有理指数幂的运算和化简
4 3
例2:用分数指数幂的形式表示下 列各式(a>0)
(1)a2 a
(2) a a
解:(1)a2
a
1
a2a2
2 1
a 2
5
a2
1
11
(2) a a (a a )2 (aa2 )2
31
31
3
(a2 )2 a2 2 a4
例3:化简下列各式(a>0,b>0)
23
5
(1)a 3 a 4 a 6
