磁性界面反演方法
地球物理反演方法的综述

地球物理反演方法的综述地球物理反演是一种利用地球物理方法来推断地下构造和物质分布的技术。
通过观测和测量地球物理场,如重力、地磁、电磁、地震等,结合数理统计和计算机模拟方法,可以对地下的地质构造、岩石性质和地下水资源等进行精确的推断。
本文将综述地球物理反演方法的原理、分类及应用。
一、地球物理反演方法的原理地球物理反演方法的原理在于根据地球物理场的观测数据,通过数学模型和计算方法,将地球物理场与地下介质属性之间的关系联系起来。
根据电磁波传播、物质密度、电阻率、磁化率等反演参数的变化规律,推断地下介质的结构和成分。
其中常用的地球物理反演方法包括重力法、磁法、电磁法、地电法和地震法等。
不同的反演方法适用于不同的地质介质和研究目标,各有其优势和限制。
二、地球物理反演方法的分类1. 重力反演法:利用重力场观测数据,通过计算物质的密度分布,来推断地下构造的方法。
重力反演法在石油勘探、地质灾害分析、水资源评价等领域具有广泛应用。
2. 磁法反演法:通过磁场观测数据,推断地下磁化率和磁性物质的空间分布。
磁法反演在矿产勘探、地震预测等方面发挥重要作用。
3. 电磁法反演法:通过电磁场观测数据,推断地下电阻率分布,来研究地下水资源、矿产和工程勘探。
电磁法反演在地下水资源评价、油气勘探、环境地球物理和岩土工程等方面有广泛应用。
4. 地电法反演法:通过电场和电位观测数据,推断地下电阻率分布,用于研究地下水位、地下水性质、污染监测和地下工程等。
地电法反演在工程地球物理勘探和水文地球物理领域具有广泛应用。
5. 地震法反演法:通过地震波在地下的传播与变化,推断地下介质的速度和密度分布,用于研究地质构造、地震预测和石油勘探等。
地震法反演是地球物理反演方法中应用最广泛的方法之一。
三、地球物理反演方法的应用地球物理反演方法广泛应用于地质探测、资源勘探、环境监测和工程勘察等领域。
以下是几个常见的应用领域:1. 石油勘探:地震反演方法可用于确定油气藏的位置、大小和分布,辅助油田开发和管理。
磁性界面起伏迭代反演方法

AbstractIn the early period of evaluation about basic structures, magnetic prospecting provided more convenient way in geophysical prospecting work, with taking advantage of its own characteristics of Less input, easy access to the field, wide range covering for unusual and effective information, data processing and shorter interpretation time. The processing and interpretation of magnetic data, the determination of the fluctuations of the magnetic geological interface and the depth of the magnetic basis, which is one of the important tasks for magnetic prospecting in in solving basin deep tectonic information. Studying the interface of magnetic strata has extremely important theoretical and practical value both in study the formation and evolution of the basin and the distribution of mineral, oil and gas resources, such as oil and gas formation, migration and occurrenceThe method of inversion magnetic interface depth can be divided into two categories: frequency domain and space domain,The spatial domain magnetic interface iterative inversion method that we studied in this paper is greatly influenced by the interface average depth of the proper selection, the deeper average interface you chose, the deeper entire interface the study will get, otherwise it will be more shallow. Therefore, it is important to determine the average depth of the interface before the inversion of the magnetic interface depth. The method of using power spectrum to determine the average depth of the interface are given in this paper, which has a big advantage of getting the result without magnetic interface material before the inversion. But before make confirmation of the initial interface value, We need to extend the observation surface field downward, Based on the iterative method proposed by the academician Xu Shizhe, this paper avoids the problem of divergence of field value effectively.Based on the theory of model test, which indicates that the magnetic interface in the spatial domain iterative inversion method is reliable, and It has certain pratical application value. At the same time, this method is used to deal with the magnetic survey data of northern south China sea, and obtains the characteristics of the magnetic basement and the fluctuation of the curie-surface in south China sea.Key words:Magnetic interface, the iterative inversion method, Power spectrum inversion method, the north of the South China Sea目录第一章绪论 (1)1.1选题背景及研究意义 (1)1.2国内外研究现状 (2)1.3主要研究内容及成果 (4)1.4技术路线 (5)第二章磁性界面正反演方法原理 (6)2.1磁性界面有限单元法正演 (6)2.2空间域磁性界面迭代反演法 (9)2.3磁性界面迭代反演的关键技术 (14)2.3.1界面平均深度的确定 (14)2.3.2迭代法位场向下延拓 (17)第三章磁性界面迭代反演方法程序设计 (19)3.1输入输出数据格式设计 (19)3.1.1平面位场数据输入格式 (19)3.1.2平面位场数据输出格式 (19)3.2磁性界面迭代反演方法程序设计 (20)3.3求取平均深度方法程序设计 (21)3.4位场向下延拓迭代法程序设计 (22)第四章理论模型试算 (24)4.1单一磁性界面模型反演 (24)4.2多磁性界面模型反演 (34)第五章实际资料处理及解释 (42)5.1研究区概况 (42)5.2岩石物性特征 (43)5.3磁性界面起伏反演 (46)第六章结论与建议 (53)6.1结论 (53)6.2建议 (53)参考文献 (55)攻读学位期间取得的研究成果 (58)致谢 (59)第一章绪论1.1 选题背景及研究意义自20世纪30年代起,磁法勘探开始应用于我国找矿试验工作中,此后随着地质工作的不断深入开展,以及数学物理理论和计算机技术的飞速发展,使得磁法勘探在方法技术、理论创新以及实际应用等各方面得到了快速发展,已成为现代地球物理方法中重要的技术手段之一。
界面反演

(2) (1) e H is = (∆ g − ∆ g ) − 2π f σ
(2)
e H is = (∆ Z − ∆ Z − 2π J i s
(1 )
)
Parker重磁界面快速正反演
把 h 反变换求得 h (2) ,则 h (1) + h (2)为h的二次近 似值,把它带入正演公式求出 ∆ g , ∆ Z 的二次近 (2) (2) 似值 ∆ Z , ∆ g 。 (3) (2) e H is 按下式求出 h(3) :h = − 2π f σ ( ∆ g − ∆ g )
Parker重磁界面快速正反演
概括:
Parker重磁界面快速正反演
界面反演的前提条件: (1)、界面上下的地层物性差足够大; (2)、地层界面起伏产生的重、磁异常足够 大;
Parker重磁界面快速正反演
界面反演的计算参数及步骤: (1)、确定地层界面的平均深度参数; (2)、确定地层界面上下地层之间的物性差参数; (3)、提取地层界面起伏对应的重、磁异常; (4)、反演计算界面深度变化。 其中:(1)、(2)、(3)是基础。
h1
地层界面
σ2
(σ 2 > σ 3 > σ 1 )
Parker重磁界面快速正反演
上面我们所讨论的是单界面的情况,如果还存 在另一个下底面,我们给出适当的条件,上述 单界面的正演公式就可以推广到双界面。
多层界面反演
下面我们以二维为例简要说一下多层界面反演。 假设地面以下密度分别为 σ 1 , σ பைடு நூலகம் , σ 3 ,密度分界面分 u 别是 ζ = ζ 1 (ξ )和 ζ = ζ 2 (ξ )。 0 , v0 分别为平均埋深
(2)
h
低磁纬度磁界面反演

断的困难 . 尤其 是 广 阔 的南 部 海域 处 于磁 赤 道 两侧 ± 0以内的低磁 纬度 区 , 磁场是 以水 平磁化 为 主 3。 地球 的斜磁化条件 , 磁性体所产生的磁异常强度 △ T是 以负
第 3 第 4期 9卷
21 0 1年 4月
同 济 大 学 学 报( 然 科 学 版) 自
J U N L O O G I N V R I Y N 球A . C O R A FT N J U I E ST ( A IS I E )
VO . 9 No 4 13 .
A .2 1 pt 0 1
文 章 编 号 : 2 33 4 2 1) 40 2 —5 0 5 —7 X(0 10 —6 00
D I1 .99 ji n 0 5 —7 x 2 1 .4 0 8 O :0 3 6 /. s .2 334 .0 1 0 .2 s
低 磁 纬 度 磁 界 面 反 演
雷 文 敏 , 健 生 吴
mod lng e i m e ho wih e s a d fex be w a o a i td t a y n l i l y f ddng
声 干扰 的维纳 滤波化 极方 法 , 引进 噪声 干扰 一 说 , 并
将其 转 化 为 稳 定 化极 转 换 的 因 素 , 程序 设 计 与 常 规 化极 相仿 , 易 实 现[ . 长 利 等 提 出 的 压 制 因 子 较 2 姚 ]
( 同济大学 海洋地质国家重点 实验室 , 上海 2 0 9 ) 0 0 2
摘 要 : 出 了低 磁纬 度 地 区化 极 存 在 的 误 差 , 究 了磁 异 常 极值与磁体的位置关系 比较复杂 , 指 研 增加了反演 和解 释推
磁法勘探 07 磁异常的反演

8
(3) 利用不同高度上磁场特征的判别法
利用不同高度上剖面磁场的空间分布特征来判别磁性体的形状, 利用不同高度上剖面磁场的空间分布特征来判别磁性体的形状,确定 空间分布特征来判别磁性体的形状 磁性体的某些参数,如埋深、 磁性体的某些参数,如埋深、宽度等 ① 利用磁异常的断面等值线的特征 断面内等值线图, 由不同高度上的剖面磁场值可绘制出 XOZ 断面内等值线图,又称为 空间等值线图。 空间等值线图。
判断脉状体倾向的多解性
4
7.2 磁性体形态的判定
一.质体、磁性体形状的初步判断 质体、
(一) 根据磁异常平面分布特征的判断 一
5
6
(2) 磁异常双分量参量图
ρ=
2 Za
+
2 Ha
µ0m [1 ± cos(ϕ + is )] = 2 4πR
上式的图形为心脏形, 上式的图形为心脏形,其心根点位于原 点,对称轴与横坐标的夹角为剖面有效 磁化倾角 is
7 磁异常的反演
本章要阐述的是:已知磁场的空间分 本章要阐述的是:已知磁场的空间分 来确定地下所对应的场源体特 布特征来确定 布特征来确定地下所对应的场源体特 如确定地质体 地质体、 征,如确定地质体、磁性体的赋存空 间位置、形状、产状及剩余质量、 间位置、形状、产状及剩余质量、磁 化强度的大小和方向等 化强度的大小和方向等。通常称为磁 异常解释理论的反演问题。 异常解释理论的反演问题。这是解决 各种地质勘探问题的重要环节。 各种地质勘探问题的重要环节。
ϕ 4 4 sin 1 + ctg 2 is 3 3
−3 / 2 64 3 13 4 16 2 ϕ = arccos ctg is + ctg is + ctg is 6 3 9 27
反演磁性地层界面的逐步剥离磁场法

p tni ed,a d d tr n ste r l fo g ei tair p i n ef c s I i r a e d sg e oe t f l l ai n ee mie ei fma n t srtga hc i tra e . n t swo k we h v e in h e c h d a
C i s , ep y .(nC iee ,2 0 5 ( ):1 hn e_.G oh s i hns ) 0 7, 0 2 6 1~6 8 e 1
反 演磁 性 地 层 界 面 的逐 步 剥 离磁 场 法
赵 百 民 ,郝天 珧 ,徐 亚 ,周 立宏 ,高 嘉 瑞 ,袁 淑 琴
2D , lD g C m a y,P t C n o p n t ,T  ̄n 3 0 8 o pn e o h a C m a yL r i d. / 0 2 0,C n a i ha
Absr c W e p o o e a me o fs p rto fma n t il tp b tp t ere e ma n tc sr t r p i ta t rp s  ̄ d o e aain o g ei fed se y se o r t v g ei tai a h c c i g itra e .T i  ̄ o u p s st a h ed i e e ae y v rain o q iae tma n t ain i ni n efc s h sme d s p o e h tt e f l s g n r td b aito fe uv ln g ei to n a u t i z — tik es a e . T e t b an te q iae t h c n s ly r h n i o tis h e v n ma n t ain f t e u i tik es a e y s p r t g he u l g ei t o nth c n s ly r b e aai t z o h — n
磁性界面反演方法
第九节 磁性界面反演方法具有一定磁性差异的地质界面,如结晶基底面、大岩体的上顶面等,是找矿勘探与基础地质研究中常见的地质现象。
磁性界面反演方法是确定这一类地质模型界面深度的方法。
磁性界面反演方法有空间域和频率域两大类。
在磁性界面反演中,常常把磁性界面划分成大量的离散二度水平棱柱体或三度直立棱柱体组合模型,由于未知参数太多不能采用直接解法,往往采用迭代法或其他方法。
空间域方法未知参数多、计算时间长、效率低。
Parker (1972,1973,1974)采用了连续模型,得出了频率域重磁位场正反演的理论公式,Oldenburg (1974)把它推广成迭代形式并做了二维计算。
由于引入快速傅立叶变换,在相同精度下,频率域方法比空间域方法反演速度至少要快一个数量级以上。
因此,频率域磁性界面的反演方法成为界面反演的一种常用方法,用于区域磁测资料解释与油气勘探中研究基底构造。
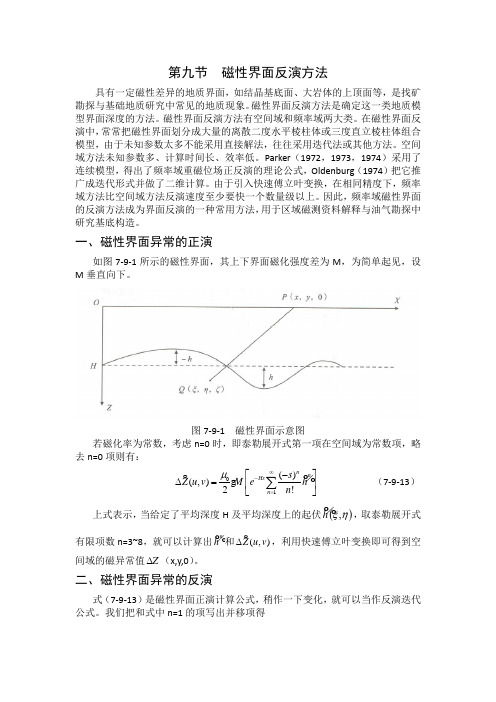
一、磁性界面异常的正演如图7-9-1所示的磁性界面,其上下界面磁化强度差为M ,为简单起见,设M 垂直向下。
图7-9-1 磁性界面示意图若磁化率为常数,考虑n=0时,即泰勒展开式第一项在空间域为常数项,略去n=0项则有: 01()(,)2!n n Hs n s Z u v M e h n μ∞-=⎡⎤-∆=⎢⎥⎣⎦∑ (7-9-13) 上式表示,当给定了平均深度H 及平均深度上的起伏 (),h ξη,取泰勒展开式有限项数n=3~8,就可以计算出 n h和 (,)Z u v ∆,利用快速傅立叶变换即可得到空间域的磁异常值Z ∆(x,y,0)。
二、磁性界面异常的反演式(7-9-13)是磁性界面正演计算公式,稍作一下变化,就可以当作反演迭代公式。
我们把和式中n=1的项写出并移项得202()()!Hs n n n e s h Z h Ms n μ∞=-=-∆-∑ (7-9-14) 若令等式右端的h 值为第i 次近似值,而等式左端的h 为第(i+1)次近似值,即为Parker 提出的迭代反演公式: 1202()[()]!Hs n i n n e s h Z h i Ms n μ∞+=--=∆-∑ (7-9-15) 实践证明,这种迭代方式每次求的都是h 值,而不是h 的修正量h ∆,不容易保证迭代收敛。
基于结构模型的磁性基底反演

]
∑ ∑ ∑ ( )( + 一1 一
F[ 一
() 1
的, 因此 , 往 出现 反演 结 果 与 实 际情 况 相 悖 的现 往
式 中 m 表示 分步 积分 的项 数 ; 指数项 展开 成 是
果满 足 给定精 度 。 针对算法 中高频 因子 影 响迭代 收敛 性 的 问
Байду номын сангаас
不 可能是 一个 精确 的模 型 , 目标应 是找 到 由 已知 其 地 质资料 及观 测数 据 所 反 映磁 性 基 底 磁性 宏 观 分 布, 采用 的方 法为概 率成像 与位 场约束 扩 展结合 的
方法。
第3卷 第3 4 期
物探 化 探 计 算技 术
21年 5 02 月
文章 编 号 :1 0 — 1 4 ( 0 2 0 —0 9 — 0 O 1 7 9 2 1 )3 2 5 8
基 于 结 构 模 型 的 磁 性 基 底 反 演
于会臻,刘 展
( 中国石 油大 学 地球 资 源与信 息 学院 , 东 青 岛 26 5) 山 6 55
关键 词 :磁性基 底 ;变磁 化 强度 ;P re 相 关 系数 ;多尺 度 分析 ak r
中图分类 号 :P 6 1 4 文 献标识 码 :A 3 . D I 0 3 6 / i n 1 0 —1 4 . 0 2 0 . 0 O :1 . 9 9 j s . O 1 7 9 2 1 . 3 1 .s
摘
要:常规磁性基底反演方法往往忽略基底磁性 变化采用常磁化强度模 型, 这里分析 了其中的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九节 磁性界面反演方法
具有一定磁性差异的地质界面,如结晶基底面、大岩体的上顶面等,是找矿勘探与基础地质研究中常见的地质现象。
磁性界面反演方法是确定这一类地质模型界面深度的方法。
磁性界面反演方法有空间域和频率域两大类。
在磁性界面反演中,常常把磁性界面划分成大量的离散二度水平棱柱体或三度直立棱柱体组合模型,由于未知参数太多不能采用直接解法,往往采用迭代法或其他方法。
空间域方法未知参数多、计算时间长、效率低。
Parker (1972,1973,1974)采用了连续模型,得出了频率域重磁位场正反演的理论公式,Oldenburg (1974)把它推广成迭代形式并做了二维计算。
由于引入快速傅立叶变换,在相同精度下,频率域方法比空间域方法反演速度至少要快一个数量级以上。
因此,频率域磁性界面的反演方法成为界面反演的一种常用方法,用于区域磁测资料解释与油气勘探中研究基底构造。
一、磁性界面异常的正演
如图7-9-1所示的磁性界面,其上下界面磁化强度差为M ,为简单起见,设M 垂直向下。
图7-9-1 磁性界面示意图
若磁化率为常数,考虑n=0时,即泰勒展开式第一项在空间域为常数项,略去n=0项则有: 01()(,)2!n n Hs n s Z u v M e h n μ∞-=⎡⎤-∆=⎢⎥⎣⎦
∑ (7-9-13) 上式表示,当给定了平均深度H 及平均深度上的起伏 (),h ξη,取泰勒展开式
有限项数n=3~8,就可以计算出 n h
和 (,)Z u v ∆,利用快速傅立叶变换即可得到空间域的磁异常值Z ∆(x,y,0)。
二、磁性界面异常的反演
式(7-9-13)是磁性界面正演计算公式,稍作一下变化,就可以当作反演迭代公式。
我们把和式中n=1的项写出并移项得
2
02()()!Hs n n n e s h Z h Ms n μ∞=-=-∆-∑ (7-9-14) 若令等式右端的h 值为第i 次近似值,而等式左端的h 为第(i+1)次近似值,即为Parker 提出的迭代反演公式: 12
02()[()]!Hs n i n n e s h Z h i Ms n μ∞+=--=∆-∑ (7-9-15) 实践证明,这种迭代方式每次求的都是h 值,而不是h 的修正量h ∆,不容易保证迭代收敛。
可以采用如下的迭代方式:
取式(7-9-15)的一级近似值: (1)02Hs e h Z Ms
μ=-∆ (7-9-16) 其中 (1)h 表示h 的一级近似值(1)h 的频谱。
把一级近似值 (1)
h
代入式(7-9-13)得 (1)(1)102()()!n n Hs n s Z Ms e h n μ∞-=⎡⎤-∆=-⎢⎥⎣⎦
∑ (7-9-17) 把 (1)Z ∆按下式求(2)h : (2)(1)02[]Hs e h
Z Z Ms μ=-∆-∆ (7-9-18) 把 (2)h
反变换求得(2)h ,则(1)(2)h h +为h 的二次近似值,把它带入式(7-9-13)求得 Z ∆的二级近似值 (2)Z ∆。
按下式求 (3)
h
: (3)(2)02(,)[(,)(,)]Hs e h u v Z u v Z u v Ms μ=-∆-∆ (7-9-19) 则(1)(2)(3)h h h ++为h 的三次近似值,再继续求 (3)Z
∆……如此下去,直到h 的第n 次近似值与第(n-1)次近似值之差满足所要求的精度为止。
这时得到的界面起伏为
()1n i i h h ==∑(7-9-20)。
