积的变化规律练习题.
第三单元积的变化规律和积不变的规律问题专项练习-四年级数学(解析版)北师大版
2023-2024学年四年级数学上册典型例题系列第三单元：积的变化规律和积不变的规律问题专项练习一、填空题。
1．甲乙两个数的积是25，如果甲数扩大4倍，乙数扩大7倍，现在的积是( )。
【答案】700【分析】一个乘数不变，另一个乘数乘几或除以几（0除外），积也乘几或除以几（0除外）。
如果两个乘数都乘几（0除外），积就乘（几×几）（0除外）。
甲数扩大4倍，乙数扩大7倍，积扩大（4×7）倍，原来的积乘（4×7）即可算出现在的积。
【详解】4×7×25＝28×25＝700甲乙两个数的积是25，如果甲数扩大4倍，乙数扩大7倍，现在的积是（700）。
【点睛】此题的解题关键是灵活应用积的变化规律求解。
2．A×B＝1000，那么（A×8）×（B÷8）＝( )，（A×10）×（B×10）＝( )。
【答案】 1000 100000【分析】积的变化规律：（1）如果一个乘数扩大到原来的几倍或缩小为原来的几分之一，另一个乘数不变，那么积也扩大相同倍数或缩小为原来的几分之一。
（2）如果一个乘数扩大到原来的几倍，另一个乘数缩小为原来的几分之一，那么积不变。
（3）如果一个乘数扩大到原来的几倍，另一个乘数也扩大到原来的几倍，那么积扩大的倍数等于两个乘数扩大的倍数的乘积，据此解答即可。
【详解】A×B＝1000，那么（A×8）×（B÷8）＝1000，（A×10）×（B×10）＝1000×10×10＝100000。
【点睛】熟练掌握积的变化规律是解答本题的关键。
3．如果A×B＝50，那么（A×20）×B＝( )；如果A比B大8，那么A ×125－125×B＝( )。
【答案】 1000 1000【分析】根据积的变化规律可知，因数A乘20，因数B不变，积应乘20。
积的变化规律练习题
积的变化规律练习题一、填空题1. 如果一个因数扩大2倍，另一个因数缩小2倍，那么积__________。
2. 如果两个因数都扩大2倍，那么积__________。
3. 如果两个因数都缩小2倍，那么积__________。
4. 在乘法里，一个因数不变，另一个因数扩大或缩小几倍（0除外），积也__________。
二、判断题1. 两个非0的因数相乘，一个因数扩大10倍，另一个因数缩小10倍，积不变。
（）2. 两个非0的因数相乘，一个因数扩大2倍，另一个因数扩大3倍，积扩大6倍。
（）3. 两个非0的因数相乘，一个因数缩小2倍，另一个因数缩小3倍，积缩小6倍。
（）4. 两个非0的因数相乘，一个因数扩大10倍，另一个因数扩大5倍，积扩大15倍。
（）三、选择题1. 两个非0的因数相乘，一个因数扩大2倍，另一个因数扩大3倍，积扩大（）倍。
A. 2B. 3C. 5D. 62. 两个非0的因数相乘，一个因数缩小3倍，另一个因数缩小2倍，积缩小（）倍。
A. 2B. 3C. 5D. 63. 在乘法里，一个因数扩大10倍，另一个因数扩大5倍，积扩大（）倍。
A. 10B. 50C. 100D. 500四、应用题1. 甲、乙两数的积是120，如果甲数扩大2倍，乙数缩小2倍，那么甲、乙两数的积是多少？2. 一个长方形的长是10厘米，宽是6厘米，如果长和宽都扩大2倍，那么面积扩大多少倍？3. 一辆汽车每小时行驶60千米，行驶了5小时，如果速度不变，行驶10小时，行驶的路程是多少？4. 一个数是24，另一个数是18，如果两个数都缩小3倍，那么它们的积是多少？五、匹配题将下列因数的变化与积的变化相匹配：A. 积扩大3倍B. 积不变C. 积缩小3倍D. 积扩大6倍E. 积缩小6倍1. 一个因数扩大2倍，另一个因数不变 ____2. 一个因数缩小2倍，另一个因数扩大2倍 ____3. 两个因数都扩大3倍 ____4. 两个因数都缩小3倍 ____5. 一个因数扩大3倍，另一个因数缩小3倍 ____六、简答题1. 请解释为什么两个非0的因数相乘，一个因数扩大几倍，另一个因数缩小相同的倍数，积不变。
积商的变化规律练习题
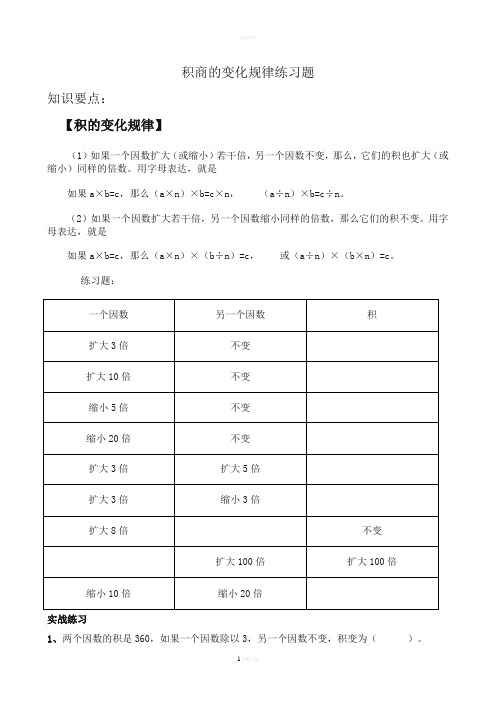
积商的变化规律练习题知识要点：【积的变化规律】（1）如果一个因数扩大（或缩小）若干倍，另一个因数不变，那么，它们的积也扩大（或缩小）同样的倍数。
用字母表达，就是如果a×b=c，那么（a×n）×b=c×n，（a÷n）×b=c÷n。
（2）如果一个因数扩大若干倍，另一个因数缩小同样的倍数，那么它们的积不变。
用字母表达，就是如果a×b=c，那么（a×n）×（b÷n）=c，或（a÷n）×（b×n）=c。
练习题：实战练习1、两个因数的积是360，如果一个因数除以3，另一个因数不变，积变为（）。
2、两个因数相乘，一个因数乘6，另一个因数不变，那么积（）。
3、两个因数相乘的积是5600，如果一个因数不变，另外一个因数除以10，那么积是（）。
4、两个数相乘是75，如果一个因数乘7，另一个因数除以7，积是（）。
5、已知A×B=400，如果A乘3，则积是（），如果B除以5，则积是（）。
6、两个数相乘，一个因数乘10，另一个因数也乘10，积（）。
7、两个因数的积是420，如果一个因数不变，另一个因数乘8，积是（）。
8、两个数相乘的积是160，如果一个因数除以2，另一个因数也除以2，积是（）。
【商或余数的变化规律】（1）如果被除数扩大（或缩小）若干倍，除数不变，那么它们的商也扩大（或缩小）同样的倍数。
用字母表达，就是如果a÷b=q，那么（a×n）÷b=q×n，（a÷n）÷b=q÷n。
（2）如果除数扩大（或缩小）若干倍，被除数不变，那么它们的商反而缩小（或扩大）同样的倍数。
用字母表达，就是如果a÷b=q，那么a÷（b×n）=q÷n，a÷（b÷n）=q×n。
人教版四年级数学上册 第四单元 第2课时 积的变化规律(课时练习题)
2023秋人教版四年级数学上册课时练习题第四单元三位数乘两位数第2课时积的变化规律一、填空题1．根据250×32＝8000，直接写出下面各算式的积。
250×64＝250×16＝250×320＝125×16＝2．已知A×B=480，如果A扩大到原来的3倍，B不变，积是；如果A不变，B除以3，积是。
3．在算式126×26中，如果第二个因数乘13，那么要使积不变。
4．两个数相乘积是630，如果一个因数乘6，另一个因数除以6，那么积是。
5．在横线上填上“>”“<”或“＝”。
24×4033×40120×34240×17180×2519×26096×532×15二、判断题6．5只猫5天吃5只老鼠，10只猫10天吃20只老鼠。
（）7．因为24×5=120，所以(24×5)×(5×5)=120。
（）8．45×40与450×4的计算结果相同。
（）9．两个因数相乘，一个因数扩大100倍，另一个因数缩小它的百分之一，积不变。
（）10．已知A×B=460，如果A不变，B除以2，则积是230。
（）三、单选题11．△×☆=300，△和☆怎样变化能使算式的积变为30000 ？下面方法正确的是（）。
A．△和☆同时乘10B．△乘10，☆乘100C．△乘10，☆除以10D．△和☆同时乘100 12．一个因数(0除外)扩大到原来的6倍，另一个因数(0除外)除以6，则积（）。
A．扩大到原来的6倍B．扩大到原来的36倍C．不变D．扩大到原来的12倍13．下面与480×40的积一样的算式是（）。
A．48×4B．24×800C．240×20D．480×414．两个因数相乘，下面说法不正确的是（）。
积的变化规律应用题专题训练
积的变化规律应用题专题训练一、积的变化规律知识点回顾1. 积的变化规律内容- 一个因数不变，另一个因数乘几或除以几（0除外），积也乘几或除以几。
例如：3×5 = 15，当一个因数3不变，另一个因数5变为10（乘2）时，积变为3×10 = 30（15×2）。
2. 应用积的变化规律解题的步骤- 首先确定哪个因数不变，哪个因数发生了变化。
- 然后根据因数的变化情况，按照积的变化规律求出积的变化结果。
二、积的变化规律应用题1. 基础题型- 题目：已知A× B = 120，如果A不变，B乘3，那么积是多少？- 解析：根据积的变化规律，一个因数A不变，另一个因数B乘3，那么积也乘3。
因为原来的积是120，所以变化后的积为120×3 = 360。
2. 综合题型- 题目：两个因数的积是360，其中一个因数除以5，另一个因数不变，积是多少？- 解析：根据积的变化规律，一个因数不变，另一个因数除以5，积也除以5。
原来的积是360，那么变化后的积为360÷5 = 72。
3. 提高题型- 题目：在乘法算式12×15 = 180中，如果12乘3，15除以3，积是多少？- 解析：- 12乘3后变为12×3 = 36。
- 15除以3后变为15÷3 = 5。
- 那么变化后的算式为36×5。
- 我们也可以根据积的变化规律来分析，一个因数乘3，另一个因数除以3，积不变。
所以积仍然是180。
4. 拓展题型- 题目：一个长方形的长是12厘米，宽是8厘米，如果长不变，宽扩大到原来的4倍，长方形的面积是多少平方厘米？（长方形面积=长×宽）- 解析：- 原来长方形的面积为12×8 = 96平方厘米。
- 因为长不变，宽扩大到原来的4倍，根据积的变化规律（这里的长和宽相当于因数，面积相当于积），面积也扩大到原来的4倍。
- 所以变化后的面积为96×4 = 384平方厘米。
积的变化规律练习题
积的变化规律练习题一、选择题1. 一个数乘以10，这个数的大小会：A. 变小B. 变大10倍C. 不变D. 无法确定2. 如果一个数乘以0.1，那么这个数的大小：A. 变小10倍B. 变大10倍C. 变大0.1倍D. 不变3. 一个数除以100，这个数的大小：A. 变大100倍B. 变小100倍C. 变大1000倍D. 变小1000倍4. 一个数乘以1，这个数的大小：A. 变大B. 变小C. 不变D. 无法确定5. 一个数除以1，这个数的大小：A. 变大B. 变小C. 不变D. 无法确定二、填空题1. 一个数乘以0.01，相当于把这个数缩小到原来的________倍。
2. 一个数除以0.1，相当于把这个数扩大到原来的________倍。
3. 一个数乘以100，相当于把这个数扩大到原来的________倍。
4. 一个数除以10，相当于把这个数缩小到原来的________倍。
5. 一个数乘以1000，相当于把这个数扩大到原来的________倍。
三、计算题1. 计算：2.5乘以40的结果。
2. 计算：0.8除以0.2的结果。
3. 计算：3.2乘以0.01的结果。
4. 计算：5除以50的结果。
5. 计算：7.5乘以100的结果。
四、应用题1. 李明有36本书，他决定将这些书平均分给他的4个朋友。
每个朋友能得到多少本书？2. 一个长方形的长是50厘米，宽是20厘米。
如果长不变，宽增加到原来的2倍，那么新的长方形的面积是多少？3. 一个工厂每天生产100个零件，如果生产效率提高到原来的2倍，那么每天能生产多少个零件？4. 一个班级有40名学生，如果每名学生需要准备10本练习册，那么这个班级一共需要准备多少本练习册？5. 一个果园里有100棵苹果树，如果每棵树平均能结出50个苹果，那么这个果园一共能收获多少个苹果？五、判断题1. 一个数乘以0.5，这个数的大小不变。
（对/错）2. 一个数除以0.5，这个数的大小不变。
积的变化规律练习题
积的变化规律练习题随着现代数学的发展，我们越来越多地需要研究和掌握关于数列和级数的概念。
而其中一个重要的概念就是积的变化规律。
在本篇文章中，我们将探讨一些关于积的变化规律的练习题，帮助读者更好地理解和应用这一概念。
问题一：求下列数列的前n项积，并讨论其变化规律。
1. 数列：1, 2, 3, 4, ...2. 数列：1, -2, 3, -4, ...3. 数列：1, 2, 4, 8, ...4. 数列：1, 1/2, 1/3, 1/4, ...解答：1. 数列：1, 2, 3, 4, ...前n项积：1, 2, 6, 24, ...规律：每一项都是前一项的积乘以当前项的值。
换言之，第n项的值等于前n-1项的积乘以n。
2. 数列：1, -2, 3, -4, ...前n项积：1, -2, -6, 24, ...规律：正负号交替出现，并且每一项都是前一项的积乘以当前项的值。
前n项积：1, 2, 8, 64, ...规律：每一项都是前一项的积乘以2。
4. 数列：1, 1/2, 1/3, 1/4, ...前n项积：1, 1/2, 1/6, 1/24, ...规律：每一项都是前一项的积除以当前项的值。
通过以上问题的解答，我们可以观察到不同数列的前n项积的变化规律。
这些规律的掌握将有助于我们在数学问题中灵活应用，进一步推导和解决更为复杂的数列和级数问题。
问题二：已知数列前n项积为Pn，求Pn与n的关系，并讨论其性质。
1. 数列：1, 2, 3, 4, ...Pn = n! (n的阶乘)性质：Pn与n的增长速度相同，即呈指数增长。
2. 数列：1, -2, 3, -4, ...Pn = (-1)^(n/2) * (n/2)! (n为偶数时) 或 Pn = 0 (n为奇数时)性质：Pn的值在奇数项时为0，在偶数项时为(n/2)!，增长速度较慢。
Pn = 2^n性质：Pn与n的增长速度相同，即呈指数增长。
4. 数列：1, 1/2, 1/3, 1/4, ...Pn = 1/n!性质：Pn与n的增长速度相同，但增长速度较慢。
小学人教四年级数学《积的变化规律》练习题
《积的变化规律》练习题
一、填空
1、一个因数不变，另一个因数乘6，则积（）
2、一个因数不变，另一个因数除以8，则积（）
3、两个数相乘的积是25，一个因数不变，另一个因数乘,9，则积是（）
4、两个数相乘的积是65，其中一个因数不变，另一个因数除以，则积是（）
5、两个数相乘，其中一个因数乘2，另一个因数乘,3，则积（）
6、两个数相乘，其中一个因数乘3，另一个因数除以,3，则积（）
7、先找出规律，再填空。
⑴58x90=5220 （2）15x7=105
58x18=( ) 45x7=( )
58x45= ( ) 75x7=( )
29x90=（） 15x63=( )
二、解决问题
1、8本新华字典重2千克，那么16本新华字典重多少千克？
2、买4支钢笔需要85元，那么买8支钢笔要多少钱？买12支钢笔呢？
3、买4千克梨需要35元，买3千克苹果需要44元，妈妈买了8千克梨和6千克苹果，一共用了多少元钱？
4、一个长方形的面积是576平方米，已知长方形的宽是18米，现在将长方形的宽增加到54米，那么增加后的长方形的面积是多少平方米？
5、一个长方形的面积是576平方米，已知长方形的长是32米，现在将长方形的长增加到64米，那么增加后的长方形的面积比原来的长方形的面积多多少平方米？。
四年级数学积的变化规律练习题
四年级数学积的变化规律练习题一、填空1、一个因数不变，另一个因数乘6，则积( )2、一个因数不变，另一个因数除以8，则积( )3、两个数相乘的积是25，一个因数不变，另一个因数乘，9，则积是( )4、两个数相乘的积是60，其中一个因数不变，另-个因数除以5，则积是( )5、两个数相乘，其中一个因数乘2，另一个因数乘3，则积( )6、两个数相乘，其中一个因数乘3，另一个因数除以，3，则积( )11.两个数相乘，一个因数乘10,另一个因数也乘10,积( )12.两个因数的积是420,如果一一个因数不变，另一个因数乘8，积是（）13.两个数相乘的积是160,如果一一个因数除以2，另一个因数也除以2，积是( )。
14.芳芳在计算乘法时，把一个因数末尾多写了1个0,结果得到800，正确的积是应该是( )。
7、两个因数的积是360,如果一个因数除以3,另-一个因数不变，积变为( )8、两个因数相乘，一个因数乘6, 另一个因数不变，那么积( )9、两个因数相乘的积是5600, 如果一个因数不变，另外一个因数除以10, 那么积是( )10、两个数相乘是75,如果- -个因数乘7，另一个因数除以7，积是( )。
11、已知AXB=400，如果A乘3,则积是( )。
如果B除以5，则积是( ) 7.24X75= 1800 17X12=20448X75= ( ) 17X24=24x150= 85X 12=48x75= 17X6=三、根据7x40=280，直接写出得数14X40 21X40 49X4028X40 35X40 7X20四、解决问题1.果园收获苹果和梨各120筐，苹果每框重35千克，梨每筐重28千克，梨比苹果少多少千克?2.光明小学操场有一个宽5米的长方形草坪要扩大面积，原来的面积为200平方米，现在长不变，宽要增加到20米，扩大后的绿地面积是多少?3.小马虎在做一道乘法算式时，把其中一个因数17看成了71，所得的积比正确的积多了540，正确的积应该是多少？。
积的变化规律 小学数学 练习题
一、选择题1. 40×60与下面（）算式结果不相同。
A．120×20 B．4×60 C．30×802. A×B＝600，如果A除以5，要使它们的乘积不变，B应该（）。
A．除以5 B．乘5 C．保持不变3. 在1.68×8.8中，去掉两个因数的小数点，积就扩大为原来的（）倍。
A．10 B．100 C．10004. 一个因数扩大3倍，另一个因数扩大2倍，积（）。
A．扩大2倍B．扩大3倍C．扩大6倍D．扩大5倍5. 两个数相乘，一个因数乘2，另一个因数除以2，则积（）。
A．不变B．乘2 C．除以2二、口算和估算6. 根据“75×32＝2400”直接写出下面各题的积。
①75×64＝②75×16＝③75×8＝④150×32＝三、填空题7. 2.7×0.05的积是( )位小数，如果把因数0.05乘3，要使积不变，另一个因数2.7应变为( )。
8. 在（）里填上“＞”“＜”或“＝”。
340000( )34万 36×20( )35×20 660÷30( )309. 两个因数的积是13.5,如果一个因数扩大到原来的5倍，另一个因数扩大到原来的2倍，积是( )．10. 两个因数的积为6.73，如果其中一个因数扩大到它的100倍，另一个因数不变，积应是___；一个因数缩小到它的，另一个因数不变，积应是___．11. 根据13×14＝182，在括号内填上适当的数。
0.13×1.4＝( ) 13×( )＝1.82 ( )×( )＝18.2四、解答题12. 一块长方形草坪，宽6米，面积是72平方米，现在长方形草坪的长不变，宽增加到30米，增加后的草坪面积是多少平方米？（要求应用积的变化规律解决问题）13. 学校草坪如图，现在要把宽增加到180米，长不变，你能计算出扩建后草坪的面积吗？14. 公园李有一块长方形的绿地（如下图）。
小学人教小学四年级的数学《积的变化规律》习题
小学人教小学四年级的数学《积的变化规律》习题《积的变化规律》习题一、填空。
1. 两个因数的积是 500，一个因数不变，另一个因数减小 5 倍，积变为（）。
2. 两个数相乘，积是 48，假如一个因数乘2，另一个因数不变，则积是（）。
3. 香蕉 10 元能够买 4 千克， 30 元能够买（）千克，买 36 千克需要（）元。
4.一个长方形绿地的面积是 480 平方米，假如长不变，将宽扩大 2 倍，绿地的面积将变为（）平方米。
5.24 ×75＝ 180017 × 12＝20448×75＝（）17 × 24＝（）75× 12＝（）17 ×6 ＝（）二、计算，并在组内谈谈发现的规律。
18×24＝ 432105 × 45＝4725（18÷ 2）×（ 24× 2）＝（105×3）×（ 45÷3）＝（18× 2）×（ 24÷ 2）＝（105÷5）×（ 45×5）＝三、在○中填上运算符号，在□中填上数。
24×75＝ 180036 × 104＝3744（24○ 6）×（ 75× 6）＝ 1800（ 36×4）×（ 104○4）＝ 3744（24○ 3）×（ 75○□）＝1800 （ 36○□）×（104○□）＝3744四、解决问题1.果园收获苹果和梨各 120 筐，苹果每筐重 35 千克，梨每筐重 28 千克，苹果比梨多收获多少千克？2. 光明小学操场有一个宽9 米的长方形草坪要扩大面积，本来的面积为540 平方米，此刻长不变，宽要增添到27 米，扩大后的绿地面积是多少？。
人教版数学四年级上册 第四单元 积的变化规律 同步练习(含答案)
小学数学人教版四年级上册4.2积的变化规律同步练习一、单选题1．已知126×22=2772，那么126×11=（）。
A．2772B．1386C．41582．在乘法算式中，两个因数都扩大10倍，积（）。
A．不变B．扩大100倍C．扩大20倍3．两数相乘，一个因数扩大2倍，另一个因数扩大3倍，那么积（）。
A．不变B．扩大5倍C．扩大6倍4．若A×360=2160，则A×3600=（）。
A．2160B．216C．21600D．2160005．一个因数乘5，另一个因数除以5，积（）。
A．乘5B．不变C．除以56．一个长方形，如果它的长扩大到原来的3倍，宽不变，那么它的面积就会扩大到原来的（）倍。
A．3B．6C．97．两个因数的乘积是150，如果一个因数不变，另一个因数扩大3倍，则积（）。
A．扩大3倍B．缩小3倍C．不变二、判断题8．960×80与96×800的积相等。
（）9．一个长方形的面积是24平方厘米，如果把它的长和宽分别扩大到原来的5倍，那么新长方形的面积是600平方厘米。
（）10．在一道乘法算式里，两个因数都乘3，积就乘6。
（）三、填空题11．在横线上填上“˃”、“= ”或“＜”。
220×3737×221 24×5+36×524+36×5250×402500×4 34×125+66×125125×（30+70）12．两个因数分别是66和8，积是，如果把一个因数缩小2倍，一个因数不变，积是。
13．根据6×70=420，写出下列各题的积。
6×35=×=420014．已知A×B=1000，如果A不变，B乘5，则积是；如果B不变，A除以2，则积是。
15．一个长方形花坛的面积是100平方米，如果它的长扩大到原来的5倍，宽不变，扩建后花坛的面积是平方米。
积的变化规律练习题
积的变化规律练习题-CAL-FENGHAI.-(YICAI)-Company One1一、想一想，填一填。
12×20=240（12×6）×（20×5）=（）（12÷3）×（20÷4）=（）（12×）×（20×）=4800（12÷）×（20÷）=40二、选择1、一个因数扩大5倍，另一个因数不变，积（）。
A、缩小5倍B、不变C、扩大5倍2、一个因数扩大5倍，另一个因数缩小5倍，积（）。
A、缩小5倍B、不变C、扩大5倍3、两数相乘，一个因数扩大2倍，另一个因数扩大3倍，那么积（）。
A、不变B、扩大5倍C、扩大6倍4、两个因数的积是60，这时一个因数缩小4倍，另一个因数不变，现在的积是（）A、240B、60C、155、一个长方形的面积为12平方米、把长扩大到原来的3倍，宽不变，扩大后的面积是（）6两个因数的积是100，把其中一个因数扩大到原来的3倍，另一个因数不变，积是（）7一个正方形的面积为12平方米、把边长扩大到原来的3倍，，扩大后的面积是（）8、两个因数的积是100，把其中一个因数扩大到原来的3倍，另一个因数也扩大到原来的3倍，积是（）9、两个因数的积是100，把其中一个因数扩大到原来的3倍，另一个因数也缩小到原来的3倍，积是（）10、一个因数不变，把其中另一个因数扩大到原来的3倍，积是90，原来两个因数的积（）11、一个因数扩大到原来的3倍，另一个因数也扩大到原来的3倍，积是90，原来两个因数的积是（）12、一个因数扩大到原来的3倍，另一个因数缩小到原来的3倍，积是90，原来两个因数的积是（）。
13、一个正方形的边长扩大到原来的5倍，面积扩大到原来的（）倍。
14、一个长方形的长扩大到原来的5倍，宽不变，面积扩大到原来的（）倍。
15、一个长方形的长扩大到原来的5倍，宽扩大到原来的2倍，面积扩大到原来的（）倍。
数学四年级上册积的变化规律练习题(含答案)
第3课时积的变化规律本课导学知识点：探索并掌握积的变化规律，能将这一规律恰当地运用于计算和解决简单的实际问题中.48×2＝ 24×5＝48×20＝ 240×25＝48×200＝ 24×250＝特别提醒：明确一个因数不变，另一个因数乘以（或除以）几，积就乘以（或除以）几.【快乐训练营】一、想一想，填一填.1.两数相乘，一个因数不变，另一个因数扩大（或缩小）若干倍，积也（）.2.两个因数的积是1500，一个因数不变，另一个因数缩小5倍，积变成（）.3.两个数相乘，积是72，如果一个因数除以2，另一个因数乘2，则积是（）.4.香蕉15元可以买12千克，30元可以买（）千克，买36千克需要（）元.二、选择.1.三位数乘两位数，积是（）A .四位数B .五位数C .四位或五位数D .六位数2.270×450的积是27×45的积的（）倍.A .10B .100C .1000D .13.要使146×□=146×10+146×8成立，那么□内的数应该是（）.三、根据6×80=480，直接写出下面各题的积.18×80= 6×160=48×80= 36×80=12×80= 12×40=12×160= 12×20=60×160= 60×800=【知识加油站】四、在○中填上运算符号，在□中填上数.1.24×75＝1800（24○6）×（75×6）＝1800（24○3）×（75○□）＝18002.36×104＝3744（36×4）×（104○4）＝3744（36○□）×（104○□）＝3744五、先计算，再会据规律写出结果.1.18×24=（18÷2）×（24×2）=（18×2）×（24÷2）=2.105×45=（105÷5）×（45×5）=（105×3）×（45÷3）=六、解决问题.1.一个长方形绿地的面积是480平方米，如果长不变，将宽扩大2倍，绿地的面积将变成多少平方米？2.光明小学操场有一个宽9米的长方形草坪要扩大面积，原来的面积为540平方米，现在宽要增加到27米，长不变，扩大后的绿地面积是多少？参考答案一、1.扩大（或缩小）若干倍 2.300 3.72 4.24 36二、1.C 2.B 3.18三、1440 960 3840 2880 960 480 1920 240 9600 48000四、1.÷×÷ 3 2.÷× 2 ÷ 2五、1.432 432 432 2.4725 4725 4725六、1.960平方米 2.2610平方米。
积的变化规律练习题
积的变化规律练习
一、填空
1、一个因数不变，另一个因数乘6，则积（）
2、一个因数不变，另一个因数除以8，则积（）
3、两个数相乘的积是25，一个因数不变，另一个因数乘,9，则积是（）
4、两个数相乘的积是65，其中一个因数不变，另一个因数除以，则积是（）
5、两个数相乘，其中一个因数乘2，另一个因数乘,3，则积（）
6、两个数相乘，其中一个因数乘3，另一个因数除以,3，则积（）
7、先找出规律，再填空。
⑴58x90=5220 （2）15x7=105
58x18=( ) 45x7=( )
58x45= ( ) 75x7=( )
29x90=（）15x63=( )
二、解决问题
1、8本新华字典重2千克，那么16本新华字典重多少千克？
2、买4支钢笔需要85元，那么买8支钢笔要多少钱？买12支钢笔呢？
3、买4千克梨需要35元，买3千克苹果需要44元，妈妈买了8千克梨和6千克苹果，一共用了多少元钱？
4、一个长方形的面积是576平方米，已知长方形的宽是18米，现在将长方形的宽增加到54米，那么增加后的长方形的面积是多少平方米？
5、一个长方形的面积是576平方米，已知长方形的长是32米，现在将长方形的长增加到64米，那么增加后的长方形的面积比原来的长方形的面积多多少平方米？。
最新人教版四年级数学上册《积的变化规律》应用题练习
人教版四年级数学上册《积的变化规律》应用题练习题
1、果园收获苹果和梨各120筐，苹果每筐重35千克，梨每筐重28千克，苹果比梨多收获多少千克？
2、光明小学操场有一个宽9米的长方形草坪要扩大面积，原来的面
积为540平方米，现在宽要增加到27米，长不变，扩大后的绿地面积是多少？
3.果园收获苹果和梨各120筐，苹果每筐重35千克，梨每筐重28千克，苹果比梨多收获多少千克？
4.光明小学操场的宽是9米，面积是540平方米，如果把宽要增加18米，长不变，扩大后的操场面积是多少？
5、一块长方形绿地的面积为560平方米，宽是8米。
如果宽增加了16米，长不变，问扩大后的面积是多少？
6、如图，正方形的边长是25厘米，阴影部分的面积是481平方厘米。
空白长方形的宽是9厘米，长是多少厘米？
8、一块长方形绿地的宽是6米，面积是180平方米，如果把这块绿地的宽增加了12米，长不变，扩大后的绿地面积是多少平方米？
9、公园里有一块长方形草坪,宽8米,占地面积是480平方米。
现在要把宽增加到64米,长不变,扩大后的草坪面积是多少平方米?。
小学数学四年级上册《积的变化规律》习题
新四年级上册《积的变化规律》习题一、基础过关1．填一填。
(1)两个数的乘积是120。
如果一个因数不变，另一个因数扩大2倍，则积是( )。
(2)因为14×26-364，所以140×26=( )。
(3)在一个自然数的末尾添两个0，就是把这个数( )100倍。
(4)观察下面的表格，你有什么发现？2．根据积的变化规律填空：36×84＝3024 15×18＝27036×42＝( ) 30×36=( )72×84＝( ) 60×18＝( )72×42＝( ) 90×9＝( )二、综合训练1．两个因数的积是256，如果把因数8改成80、800，积分别是多少？2．一辆汽车4小时行260千米。
照这样的速度，2小时、8小时、20小时分别行多少千米？3．两座城市相距300千米，一辆汽车从一座城市驶向另一座城市，去时用了6小时，返回时少用了1小时。
(l)去的时候这辆汽车的速度是多少？(2)返回时的速度是多少？4．张叔叔从家骑自行车去单位用了40分钟。
他先以250米／分的速度骑了15分钟，又以230米／分的速度骑了25分钟。
5．小强他们打算买8个冰淇淋和12支雪糕，应付多少钱？6．这个体育馆共有32个看台，每个看台能坐598人。
你能估计出这个体育馆一共可以坐多少人吗？三、拓展应用1．《小学奥数》每套162元，<中外数学家的故事》每套89元。
学校图书室要购进这两种书各18套，一共要花多少钱？2..商店有三种书包，它们的价格分别22元、31元、37元。
学校大队辅导员带着同学们的1912元钱为山区的小伙伴买59个同样的书包，要求剩余的钱要尽量少。
请你帮辅导员估算一下，应该买哪一种书包最合适？3．我会思考。
一个工程队4天铺路的长度分别为572米、650米、612米、584米，这个工程队30天铺出的路程为多少米？参考答案一、基础过关1．填一填。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、想一想，填一填。
12×20=240
（12×6）×（20×5）=（）
（12÷3）×（20÷4）=（）
（12×）×（20×）=4800
（12÷）×（20÷）=40
二、选择
1、一个因数扩大5倍，另一个因数不变，积（）。
A、缩小5倍
B、不变
C、扩大5倍
2、一个因数扩大5倍，另一个因数缩小5倍，积（）。
A、缩小5倍
B、不变
C、扩大5倍
3、两数相乘，一个因数扩大2倍，另一个因数扩大3倍，那么积（）。
A、不变
B、扩大5倍
C、扩大6倍
4、两个因数的积是60，这时一个因数缩小4倍，另一个因数不变，现在的积是（）
A、240
B、60
C、15
5、一个长方形的面积为12平方米、把长扩大到原来的3倍，宽不变，扩大后的面积是（）
6两个因数的积是100，把其中一个因数扩大到原来的3倍，另一个因数不变，积是（）
7一个正方形的面积为12平方米、把边长扩大到原来的3倍，，扩大后的面积是（）
8、两个因数的积是100，把其中一个因数扩大到原来的3倍，另一个因数也扩大到原来的3倍，积是（）
9、两个因数的积是100，把其中一个因数扩大到原来的3倍，另一个因数也缩小到原来的3倍，积是（）
10、一个因数不变，把其中另一个因数扩大到原来的3倍，积是90，原来两个因数的积（）
11、一个因数扩大到原来的3倍，另一个因数也扩大到原来的3倍，积是90，原来两个因数的积是（）
12、一个因数扩大到原来的3倍，另一个因数缩小到原来的3倍，积是90，原来两个因数的积是（）。
13、一个正方形的边长扩大到原来的5倍，面积扩大到原来的（）倍。
14、一个长方形的长扩大到原来的5倍，宽不变，面积扩大到原来的（）倍。
15、一个长方形的长扩大到原来的5倍，宽扩大到原来的2倍，面积扩大到原来的（）倍。
16、一个因数缩小5倍，另一个因数不变，积（）。
A、缩小5倍
B、不变
C、扩大5倍。