Mathematica线性回归和非线性拟合
项目八假设检验回归分析与方差分析

项目八 假设检验、回归分析与方差分析实验2 回归分析实验目的 学习利用Mathematica 求解一元线性回归问题. 学会正确使用命令线性回归Regress, 并从输出表中读懂线性回归模型中各参数的估计, 回归方程, 线性假设的显著性检验结果, 因变量Y 在预察点0x 的预测区间等.基本命令1.调用线性回归软件包的命令<<Statistics\LinearRegression.m 输入并执行调用线性回归软件包的命令<<Statistics\LinearRegression.m或调用整个统计软件包的命令<<Statistics`2.线性回归的命令Regress一元和多元线性回归的命令都是Regress. 其格式是Regress[数据, 回归函数的简略形式, 自变量,RegressionReport(回归报告)->{选项1,选项2,选项3,…}]注: 回归报告中包含BestFit(最佳拟合,即回归函数), ParameterCITable(参数的置信区间表), PredictedResponse(因变量的预测值), SinglePredictionCITable(因变量的预测区间), FitResiduals(拟合的残差), SummaryReport(总结性报告)等.3.抹平“集合的集合”的命令Flatten命令Flatten[A]将集合的集合A 抹平为只有一个层次的集合. 例如, 输入Flatten[{{1,2,3},{1,{3}}}]则输出{1,2,3,1,3}.4.非线性拟合的命令NonlinearFit 使用的基本格式为NonlinearFit [数据, 拟合函数, (拟合函数中的)变量集, (拟合函数中的)参数, 选项] 注: 拟合函数中既有变量又有参数, 变量的个数要与数据的形式相应. 参数集中往往需 要给出各参数的初值. 选项的内容主要是指定拟合算法、迭代次数和精度.实验举例例2.1 (教材 例2.1) 某建材实验室做陶粒混凝土实验室中, 考察每立方米)(3m 混凝土的水泥用量(kg)对混凝土抗压强度)/(2cm kg 的影响, 测得下列数据:7.894.866.822.804.771.742602502402302202103.711.686.646.613.589.56200190180170160150yx y x 抗压强度水泥用量抗压强度水泥用量(1) 画出散点图;(2) 求y 关于x 的线性回归方程,ˆˆˆx b a y+=并作回归分析; (3) 设2250=x kg, 求y 的预测值及置信水平为0.95的预测区间.先输入数据:aa = {{150,56.9},{160,58.3},{170,61.6},{180,64.6},{190,68.1},{200,71.3},{210,74.1},{220,77.4},{230,80.2},{240,82.6},{250,86.4},{260,89.7}};(1) 作出数据表的散点图. 输入ListPlot[aa,PlotRange->{{140,270},{50,90}}]则输出图2.1.图2.1(2) 作一元回归分析, 输入Regress[aa,{1,x},x,RegressionReport->{BestFit,ParameterCITable,SummaryReport}]则输出{BestFit->10.2829+0.303986x, ParameterCITable->Estimate SE CI 1 10.2829 0.850375 {8.388111,12.1776}, x 0.303986 0.00409058 {0.294872,0.3131} ParameterTable->Esimate SE Tstat PValue 110.28290.85037512.09222.71852710-⨯,x 0.303986 0.00409058 74.3137 4.884981510-⨯ Rsquared->0.998193,AdjustedRSquared->0.998012, EstimatedVariance->0.0407025,ANOV A Table->DF SumOfSq MeanSq Fratio PValue Model1 1321.43 1321.435522.524.773961510-⨯Error10 2.39280.23928Total 11 1323.82现对上述回归分析报告说明如下:BestFit(最优拟合)-> 10.2829+0.303986x 表示一元回归方程为x y 303986.02829.10+=;ParameterCITable(参数置信区间表)中: Estimate 这一列表示回归函数中参数a , b 的点估计为aˆ=10.2829 (第一行), b ˆ= 0.303986 (第二行); SE 这一列的第一行表示估计量a ˆ的标准差为0.850375, 第二行表示估计量bˆ的标准差为0.00409058; CI 这一列分别表示a ˆ的置信水平为0.95的置信区间是(8.388111,12.1776), bˆ的置信水平为0.95的置信区间是 (0.294872,0.3131).ParameterTable(参数表)中前两列的意义同参数置信区间表; Tstat 与Pvalue 这两列的第一行表示作假设检验(t 检验):0:,0:10≠=a H a H 时, T 统计量的观察值为12.0922, 检验统计量的P 值为2.71852710-⨯, 这个P 值非常小, 检验结果强烈地否定0:0=a H , 接受0:1≠a H ; 第二行表示作假设检验(t 检验): ,0:0=b H 0:1≠b H 时T 统计量的观察值为74.3137, 检验统计量的P 值为 4.884981510-⨯, 这个P 值也非常小, 检验结果强烈地否定,0:0=b H 接受0:1≠b H .Rsquared->0.998193, 表示.998193.0)()(2==总平方和回归平方和SST SSR R 它说明y 的变化有99.8%来自x 的变化; AdjustedRSquared->0.998012, 表示修正后的=2~R 0.998012.EstimatedVariance->0.0407025, 表示线性模型),0(~,2σεεN bx a y ++=中方差2σ的估计为0.0407025.ANOV A Table(回归方差分析表)中的DF 这一列为自由度: Model(一元线性回归模型)的自由度为1, Error(残差)的自由度为,102=-n Total(总的)自由度为.111=-nSumOfSq 这一列为平方和: 回归平方和=SSR 1321.43, 残差平方和=SSE 2.3928,总的平方和=+=SSE SSR SST 1323.82;MeanSq 这一列是平方和的平均值, 由SumOfSq 这一列除以对应的DF 得到, 即.23928.02,43.13211=-===n SSEMSE SSR MSR FRatio 这一列为统计量MSEMSRF =的值, 即.52.5522=F 最后一列表示统计量F 的P 值非常接近于0. 因此在作模型参数)(b =β的假设检验(F 检验):0:;0:10≠=ββH H 时, 强烈地否定0:0=βH , 即模型的参数向量.0≠β因此回归效果 非常显著.(3) 在命令RegressionReport 的选项中增加RegressionReport->{SinglePredictionCITable}就可以得到在变量x 的观察点处的y 的预测值和预测区间. 虽然0.14=x 不是观察点, 但是可以用线性插值的方法得到近似的置信区间. 输入aa=Sort[aa]; (*对数据aa 按照水泥用量x 的大小进行排序*)regress2=Regress[aa,{1,x},x,RegressionReport->{SinglePredictionCITable}](*对数据aa 作线性回归, 回归报告输出y 值的预测区间*)执行后输出{SinglePredictionCITable-> Observed PredictedSE CI56.9 55.8808 0.55663 {54.6405,57.121} 58.3 58.92060.541391 {57.7143,60.1269} 61.6 61.9605 0.528883 {60.7821,63.1389} 64.6 65.00030.519305 {63.8433,66.1574} 68.1 68.0402 0.51282 {66.8976,69.1828} 71.3 71.0801 0.509547 {69.9447,72.2154}} 74.1 74.1199 0.509547 {72.9846,75.2553} 77.4 77.1598 0.51282 {76.0172,78.3024} 80.2 80.1997 0.519305 {79.0426,81.3567} 82.6 83.2395 0.528883 {82.0611,84.4179} 86.4 86.2794 0.541391 {85.0731,87.4857} 89.7 89.3192 0.55663 {88.079,90.5595}上表中第一列是观察到的y 的值, 第二列是y 的预测值, 第三列是标准差, 第四列是相应的预测区间(置信度为0.95). 从上表可见在)4.77(220==y x 时, y 的预测值为77.1598, 置信度为0.95的预测区间为(76.0172,75.2553), 在)2.80(230==y x 时, y 的预测值为80.1997, 置信度为0.95的预测区间为{79.0426,81.3567}. 利用线性回归方程, 可算得=0x 225时, y 的预测值为78.68, 置信度为0.95的预测区间为(77.546, 79.814).利用上述插值思想, 可以进一步作出预测区间的图形. 先输入调用图软件包命令<<Graphics`执行后再输入{observed2,predicted2,se2,ci2}=Transpose[(SinglePredictionCITable/.regress2)[[1]]];(*取出上面输出表中的四组数据, 分别记作observed2,predicted2,se2,ci2*) xva12=Map[First,aa];(*取出数据aa 中的第一列, 即数据中x 的值, 记作xva12*) Predicted3=Transpose[{xva12,predicted2}];(*把x 的值xva12与相应的预测值predicted2配成数对, 它们应该在一条回 归直线上*)lowerCI2=Transpose[{xva12,Map[First,ci2]}];(*Map[First,ci2]取出预测区间的第一个值, 即置信下限. x 的值xva12与相应 的置信下限配成数对*)upperCI2=Transpose[{xva12,Map[Last,ci2]}];(*Map[Last,ci2]取出预测区间的第二个值, 即置信上限. x 的值xva12与相应的置信上限配成数对*)MultipleListPlot[aa,Predicted3,lowerCI2,upperCI2,PlotJoined->{False,True,True,True},SymbolShape->{PlotSymbol[Diamond],None,None, None}, PlotStyle->{Automatic,Automatic,Dashing[{0.04,0.04}], Dashing[{0.04,0.04}]}](*把原始数据aa 和上面命令得到的三组数对predicted3,lowerCI2,upperCI2 用多重散点图命令MultipleListPlot 在同一个坐标中画出来. 图形中数据 aa 的散点图不用线段连接起来, 其余的三组散点图用线段连接起来, 而 且最后两组数据的散点图用虚线连接.*)则输出图2.2.图2.2从图形中可以看到, 由Y 的预测值连接起来的实线就是回归直线. 钻石形的点是原始数 据. 虚线构成预测区间.多元线性回归例2.2 (教材 例2.2) 一种合金在某种添加剂的不同浓度下, 各做三次试验, 得到数据如下表:8.323.327.298.277.288.301.306.321.313.274.297.312.318.292.250.300.250.200.150.10Yx 抗压强度浓度(1) 作散点图;(2) 以模型),0(~,22210σεεN x b x b b Y +++=拟合数据, 其中2210,,,σb b b 与x 无关;(3) 求回归方程,ˆˆˆˆ2210x b x b b y ++=并作回归分析. 先输入数据bb={{10.0,25.2},{10.0,27.3},{10.0,28.7},{15.0,29.8},{15.0,31.1},{15.0,27.8},{20.0,31.2},{20.0,32.6}, {20.0,29.7},{25.0,31.7},{25.0,30.1},{25.0,32.3}, {30.0,29.4},{30.0,30.8},{30.0,32.8}};(1) 作散点图, 输入ListPlot[bb,PlotRange->{{5,32},{23,33}},AxesOrigin->{8,24}]则输出图2.3.图2.3(2) 作二元线性回归, 输入Regress[bb,{1,x,x^2},x,RegressionReport->{BestFit,ParameterCITable,SummaryReport}](*对数据bb 作回归分析, 回归函数为,2210x b x b b ++用{1,x,x^2}表示, 自变量为x, 参数0b ,1b ,2b 的置信水平为0.95的置信区间)执行后得到输出的结果:{bestFit->19.0333+1.00857x-0.020381x 2, ParameterCITable->Estimate SE CI119.0333 3.27755{11.8922,26.1745} x 1.00857 0.356431{0.231975,1.78517}x 2 -0.0203810.00881488{-0.0395869,-0.00117497}ParameterTable->Estimate SE Tstat PValue 119.03333.277555.807180.0000837856x 1.00857 0.356431 2.82964 0.0151859 x 2 -0.0203810.00881488-2.312110.0393258Rsquared->0.614021,AdjustedRSquared->0.549692, EstimatedVariance->2.03968,ANOV A Table->DF SumOfSqMeanSq Fratio PValue Mode1 2 38.937119.4686 9.54490.00330658Error 12 24.47622.03968Total14 63.4133从输出结果可见: 回归方程为,020381.000857.10333.192x x Y -+=.020381.0ˆ,00857.1ˆ,0333.19ˆ210-===b b b 它们的置信水平为0.95的置信区间分别是 (11.8922,26.1745),(0.231975,1.78517),(-0.0395869,-0.00117497).假设检验的结果是: 在显著性水平为0.95时它们都不等于零. 模型),0(~,22210σεεN x b x b b Y +++=中,2σ的估计为2.03968. 对模型参数T b b ),(21=β是否等于零的检验结果是: .0≠β因此回归效果显著.非线性回归例2.3 下面的数据来自对某种遗传特征的研究结果, 一共有2723对数据, 把它们分成8类后归纳为下表.36.1937.1991.2079.2115.2342.257.2908.3887654321917461203246071021579y x 遗传性指标分类变量频率研究者通过散点图认为y 和x 符合指数关系:,c ae y bx += 其中c b a ,,是参数. 求参数c b a ,,的最小二乘估计.因为y 和x 的关系不是能用Fit 命令拟合的线性关系, 也不能转换为线性回归模型. 因此考虑用(1)多元微积分的方法求c b a ,,的最小二乘估计; (2)非线性拟合命令NonlinearFit 求c b a ,,的最小二乘估计.(1) 微积分方法 输入Off[Genera1::spe11] Off[Genera1::spe111] Clear[x,y,a,b,c]dataset={{579,1,38.08},{1021,2,29.70},{607,3,25.42},{324,4,23.15},{120,5,21.79},{46,6,20.91},{17,7,19.37},{9,8,19.36}}; (*输入数据集*) y[x_]:=a Exp[b x]+c (*定义函数关系*)下面一组命令先定义了曲线c ae y bx +=与2723个数据点的垂直方向的距离平方和, 记为).,,(c b a g 再求),,(c b a g 对c b a ,,的偏导数,,,cgb g a g ∂∂∂∂∂∂分别记为.,,gc gb ga 用FindRoot 命令解三个偏导数等于零组成的方程组(求解c b a ,,). 其结果就是所要求的c b a ,,的最小二乘估计. 输入Clear[a,b,c,f,fa,fb,fc]g[a_,b_,c_]:=Sum[dataset[[i,1]]*(dataset[[i,3]]-a*Exp[dataset[[i,2]]*b]-c)^2,{i,1,Length[dataset]}] ga[a_,b_,c_]=D[g[a,b,c],a]; gb[a_,b_,c_]=D[g[a,b,c],b]; gc[a_,b_,c_]=D[g[a,b,c],c]; Clear[a,b,c]oursolution=FindRoot[{ga[a,b,c]==0,gb[a,b,c]==0,gc[a,b,c]==0},{a,40.},{b,-1.},{c,20.}](* 40是a 的初值, -1是b 的初值, 20是c 的初值*)则输出{a->33.2221,b->-0.626855,c->20.2913} 再输入yhat[x_]=y[x]/.oursolution则输出20.2913+33.2221x e 626855.0这就是y 和x 的最佳拟合关系. 输入以下命令可以得到拟合函数和数据点的图形:p1=Plot[yhat[x],{x,0,12},PlotRange->{15,55},DisplayFunction->Identity]; pts=Table[{dataset[[i,2]],dataset[[i,3]]},{i,1,Length[dataset]}]; p2=ListPlot[pts,PlotStyle->PointSize[.01],DisplayFunction->Identity]; Show[p1,p2,DisplayFunction->$DisplayFunction];则输出图2.4.图2.4(2) 直接用非线性拟合命令NonlinearFit 方法 输入data2=Flatten[Table[Table[{dataset[[j,2]],dataset[[j, 3]]},{i,dataset[[j,1]]}],{j,1,Length[dataset]}],1]; (*把数据集恢复成2723个数对的形式*)<<Statistics`w=NonlinearFit[data2,a*Exp[b*x]+c,{x},{{a,40},{b,-1},{c,20}}]则输出x e 626855.02221.332913.20-+这个结果与(1)的结果完全相同. 这里同样要注意的是参数c b a ,,必须选择合适的初值.如果要评价回归效果, 则只要求出2723个数据的残差平方和.)ˆ(2∑-i i yy 输入 yest=Table[yhat[dataset[[i,2]]],{i,1, Length[dataset]}];yact=Table[dataset[[i,3]],{i,1,Length[dataset]}]; wts=Table[dataset[[i,1]],{i,1,Length[dataset]}]; sse=wts.(yact-yest)^2 (*作点乘运算*)则输出59.9664即2723个数据的残差平方和是59.9664. 再求出2723个数据的总的相对误差的平方和.]ˆ/)ˆ[(2∑-i i i y yy 输入 sse2=wts.((yact-yest)^2/yest) (*作点乘运算)则输出2.74075由此可见, 回归效果是显著的.实验习题1.某乡镇企业的产品年销售额x 与所获纯利润y 从1984年的数据(单位:百万元)如下表3.225.207.174.157.135.117.94.83.84.65.43.349.328.294.241.214.176.147.104.95.71.69493929190898887868584y x 纯利润销售额年度 试求y 对x 的经验回归直线方程, 并作回归分析.2.在钢线碳含量对于电阻的效应的研究中, 得到以下数据268.236.2221191815/95.080.070.055.040.030.010.0%/Ωμy x 电阻碳含量试求y 对x 的经验回归直线方程, 并作简单回归分析.(1) 画出散点图;(2) 求y 关于x 的线性回归方程,ˆˆˆx b a y+=并作回归分析; (3) 求0.14=x 时y 的置信水平为0.95的预测区间.4.下面给出了某种产品每件平均单价Y (单位:元)与批量x (单位:件)之间的关系的一组数 据18.120.121.124.126.130.140.148.155.165.170.181.1908075706560504035302520y x(i)作散点图. (ii)以模型),0(~,22210σεεN x b x b b Y +++=拟合数据, 求回归方程,ˆˆˆˆ2210x b x b b Y ++=并作简单回归分析.]。
2 利用Mathcad2000进行多元线性回归分析

2 利用Mathcad2000进行多元线性回归分析【例】同Excel2000例。
第一步,输入数据或从Excel调入数据(图1)。
图1 录入或调入的数据第二步,建立自变量矩阵Mx和因变量矩阵My。
⑴定义矩阵。
输入“Mx:=”,然后在Matrix工具栏中选择矩阵符号(图2)并单击,弹出一个Insert Matrix(插入矩阵)对话框(图3),设Rows(行)数为18——与样本数或时间序列长度对应;设Columns(列)数为3——与自变量个数一致。
点击OK确定,便会生成一个由Mx定义的自变量矩阵。
用类似的方法生成一个由My定义的因变量矩阵(图4)。
图2 Matrix工具栏中矩阵符号的位置图3 Insert Matrix对话框Mx⎛⎝⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭:=My⎛⎝⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭:=图4 变量矩阵⑵粘贴数据。
在数据表中选中全部的自变量,点右键,选择Copy Selection(图5)。
然后选中矩阵Mx中的全部点位,粘贴(Paste)(图6),即可生成矩阵自变量Mx;用类似的方法不难生成因变量矩阵My(图7)。
图5 选中自变量的全部数据作拷贝选择图6 将从数据表中拷贝的自变量粘贴进来Mx57.8258.0559.1563.8365.3667.2666.9267.7975.6580.5779.0280.5286.8895.48109.71126.5138.89160.5627.0528.8933.0235.2324.9432.9530.3538.747.9954.1858.7359.8564.5770.9781.5494.01103.23119.3314.5416.8312.2612.8711.6512.8710.810.9314.7117.5620.3218.6725.3425.0629.6943.8648.960.98⎛⎝⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭:=My3.093.43.883.93.223.763.594.034.344.654.785.045.596.017.0310.0310.8312.9⎛⎝⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭:=图7 自变量和因变量矩阵⑶ 数据拟合。
运用Matlab和SPSS软件求解回归分析的比较研究

运用Matlab和SPSS软件求解回归分析的比较研究作者:肖郑利来源:《中国科技博览》2014年第30期[摘要]在研究变量之间的相关关系时要用到回归分析。
本文以一个给定的线性回归模型,分别介绍Matlab软件和SPSS软件求解过程,两者的计算结果是一样的。
分析过程可知:Matlab的优势是函数丰富、编程灵活;SPSS的优点在于界面友好、操作简单。
均为回归分析提供了全面的解决方案[关键词]线性回归;Matlab;SPSS;统计量中图分类号:C66 文献标识码:A 文章编号:1009-914X(2014)30-0169-02回归分析是研究变量之间相关关系的数学方法,是将实际问题中体现的相关关系转化为确定性关系来解决的过程。
常见的实际问题有:生活中近似关系的表达,通过观测数据对固定数值的预测和控制,根据测量数据对生产工艺进行优化等等。
回归分析按照自变量的数量可以分为一元回归和多元回归;按照方程形式可以分为线性回归和非线性回归。
随着计算机技术的应用发展,有多种软件可以求解回归方程并进行分析,常用的有数学软件Mathematica、科学计算软件Matlab、数据统计分析软件SPSS和表格应用软件excel等等。
本文以简单的一元线性回归为例,分别利用Matlab软件和SPSS软件求解分析,并进行比较研究。
首先给出一个实际案例。
考察温度x对产量y的影响,测得下列10组数据:(见表1)分析y关于x的线性回归方程,检验回归效果是否显著。
1 Matlab软件求解回归分析1.1 Matlab软件介绍Matlab软件有总包和若干个工具箱,可以进行数值分析、统计、优化,可以完成信号处理、图像处理等领域的计算和图形显示。
它用函数形式将各类数学分支的算法分类,使用时可设计参数再选择调用相应的函数,快速而准确的解决问题。
1.2 Matlab软件中回归分析命令介绍线性回归的命令是regress,用以确定回归系数的点估计值:b=regress(Y,X);求回归系数的点估计和区间估计,并进行检验,直接用命令:[b,bint,r,rint,stats]=regress(Y,X,alpha),其中alpha是显著性水平,缺省时默认为0.05,bint是区间估计,r是残差,rint 计算残差的置信区间,stats记录检验回归模型的统计量,有四个数值分别是相关系数R、F检验值、与F对应的概率P以及方差的估计值;还可以画残差计算其置信区间,命令为:rcoplot (r,rint)。
mathematica中数据拟合算符的用法

mathematica中数据拟合算符的用法在数据处理中常常设法用一个函数按照某种法则去描述一组数据,这就是数据拟合。
上面介绍的最小二乘法就是一种最常用的数据拟合方法。
mathematica中最基本的数据拟合算符是fit[ ] ,语法为fit[数据,拟合函数的基函数列表,变量]线性函数拟合的基函数为1,x ,n阶多项式拟合的基函数是1,x,x2,…xn。
例一册书的成本费y与印刷的册数x有关,统计数据如下:xi(千册) 1 2 3 4 5 6 7 8 9 10yi(元)10.15 5.52 4.08 2.85 2.11 1.62 1.41 1.30 1.21 1.15试用y=a+ 去拟合上述数据。
mathematica程序及运行结果如下:data={10.15,5.52,4.08,2.85,2.11,1.62,1.41,1.30,1.21,1.15};fit[data,{1,1/x},x]四、实验内容与要求1 画出实验问题的数据图,并粗略估计这些数据与什么类型的函数比较吻合?2 取经验公式为线性函数y=ax+b 按照最小二乘法的原理用mathematica编程解实验问题。
3 取经验公式为y=ax+b +c sin[ x]+d cos[ x] ,用mathematica中算符fit[]来求解实验问题,并与内容2的精度比较,对比实际情况,你能得出什么?五、操作提示12 拟合程序及运行结果如下:预测程序及运行结果如下:3 程序及运行结果如下:计算两种经验公式的精度可以看出第二种较好,这与客流量呈季节被动变动的实际情况吻合。
怎样用mathematica拟合二元函数?数据拟合由一组已知数据(xk,yk)(k=1,2,…,n),求函数的近似解析式y=f(x),就是数据拟合问题,当然函数还可以是多元的。
Mathematica提供了进行数据拟合的函数:Fit[data,funs,vars] 对数据data用最小二乘法求函数表funs中各函数的一个线性组合作为所求的近似解析式,其中vars是自变量或自变量的表。
《非线性拟合》课件

梯度下降法
梯度下降法是一种迭代优
1
化算法,通过不断迭代更
新参数来最小化目标函数
。
4
梯度下降法的缺点是收敛 速度较慢,可能需要多次 迭代才能找到最优解,且 对初始值敏感。
梯度下降法的核心思想是
2
沿着负梯度的方向搜索参
数空间,以最快的方式找
到最小值点。
3 梯度下降法的优点是简单
易行,适用于大规模数据
的拟合,而且能够给出全
考虑模型的复杂度和解释性
在选择模型时,需平衡模型的复杂度和解释性。
参数估计
STEP 02
STEP 01
参数优化
参数初始值设定
为模型参数设定合适的初 始值。
STБайду номын сангаасP 03
参数诊断
对参数进行诊断,确保参 数的合理性和有效性。
使用合适的优化算法对模 型参数进行优化。
模型验证
内部验证
使用交叉验证等方法对模型进行内部验证,评估模型 的性能。
《非线性拟合》PPT 课件
• 非线性拟合的基本概念 • 非线性拟合的方法 • 非线性拟合的步骤 • 非线性拟合的实例 • 非线性拟合的注意事项
目录
Part
01
非线性拟合的基本概念
定义与特性
总结词
非线性拟合的定义、特性
详细描述
非线性拟合是指通过非线性函数对数据进行拟合的方法。它能够更好地描述现实世界中的复杂关系,因为现实世 界中的许多现象都受到非线性因素的影响。非线性拟合具有更高的灵活性和适应性,能够更好地捕捉数据中的复 杂模式和结构。
Part
03
非线性拟合的步骤
数据准备
数据收集
收集相关数据,确保数据 的准确性和完整性。
在mathematica中的合并两组数据求解回回归模型-概述说明以及解释

在mathematica中的合并两组数据求解回回归模型-概述说明以及解释1.引言1.1 概述在数据分析和预测建模中,合并多组数据并求解回归模型是一个常见的需求。
通过合并两组数据,我们可以获得更全面和准确的数据集,进而提高回归模型的预测能力。
本文将介绍如何在Mathematica中使用其丰富的函数和工具来实现数据的合并和回归模型求解。
首先,我们将讨论数据合并的重要性和意义。
数据的合并可以将来自不同来源、不同时间段或不同数据集的信息整合在一起,从而得到更为全面和具有代表性的数据集。
这样一来,我们可以从更广泛的角度来观察和分析数据,发现其中的规律和趋势。
合并数据还可以避免信息的重复和缺失,提高数据的完整性和一致性。
接下来,我们将介绍回归模型的求解方法。
回归分析是一种用于描述和预测变量间关系的统计分析方法,通过建立数学模型来解释自变量对因变量的影响。
回归模型可以帮助我们理解变量之间的相关性,并用于预测和预测未来的数值。
最后,我们将详细讲解如何在Mathematica中应用这些方法来合并两组数据和求解回归模型。
Mathematica是一种功能强大且易于使用的数学建模和数据分析软件,提供了丰富的函数和工具,可以简化和加速我们的工作流程。
我们将演示如何使用Mathematica中的内置函数来导入、处理和合并数据,以及如何使用回归分析函数来求解回归模型。
通过本文的学习,读者将了解到如何合并两组数据并求解回归模型的基本方法和步骤,以及如何利用Mathematica工具来简化和加快这一过程。
这将帮助读者在进行数据分析和建模时更加高效和准确。
在结论部分,我们还将对实验结果进行分析,并讨论方法的优劣和可能的改进方向,以期为读者提供更多的思考和启示。
综上所述,本文的目的是介绍如何在Mathematica中合并两组数据并求解回归模型。
希望本文能够帮助读者更好地理解和应用这些方法,从而在数据分析和建模的过程中取得更好的结果。
Mathematica偏导数最小二乘法(线性回归)
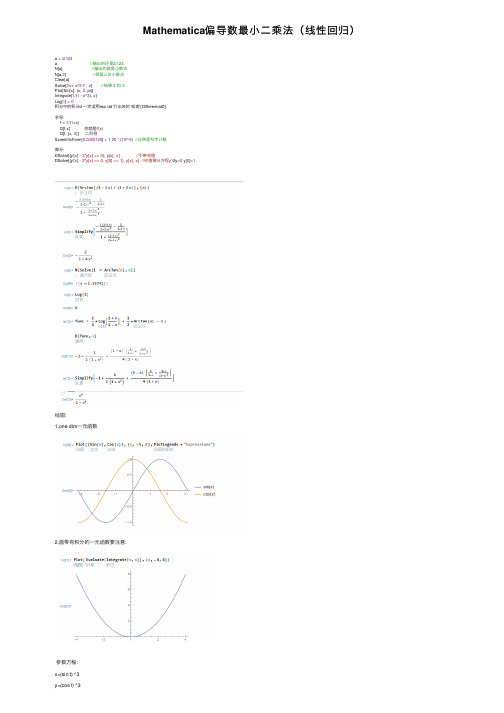
Mathematica偏导数最⼩⼆乘法(线性回归)a = 2/123a //输出的还是2/123N[a] //输出的就是⼩数点N[a,2] //保留三位⼩数点Clear[a]Solve[2== x^2-7 , x] //结果-3 和 3Plot[Sin[x], {x, 0, pi}]Integrate[1/(1 - x^3), x]Log[1] = 0积分中的积分d ⼀定适⽤esc dd 打出来的或者\[DifferentialD].求导:f = 1/(1+x)D[f,x] 也就是f'(x)D[f, {x, 2}] ⼆阶导ScientificForm[0.0000125] = 1.25 * (10^-5) //这种是科学计数微分:DSolve[{y'[x] - 2*y[x] == 0}, y[x], x] //不带初值DSolve[{y'[x] - 2*y[x] == 0, y[0] == 1}, y[x], x] //初值微分⽅程y'-2y=0 y[0]=1绘图:1,one dim⼀元函数2,画带有积分的⼀元函数要注意:参数⽅程:x=(sin t) ^3y=(cos t) ^3同时绘制2个参数图:参数图并且求导:三维参数图:r(t ) = (cos t)i + (sin t)j + (sin2t)kz = x^2 + y^2ContourPlot3D[x^2 + y^2 == z, {x, -3, 3}, {y, -3, 3}, {z, -18, 18}, PlotLabel -> "x^2+y^2=z"]2,:z^2 + x^2 -y^2=13 ⼆元函数:⼆元函数的图形是三维坐标空间的⼀个点集. 所以⼆元函数形式为f(x,y) ,f(x,y)= c ,就是等位线(等⾼线)⽅程。
画 (a)⼆元函数给定的曲⾯,(b)并且画等⾼线(等位线),(c)并且画f 给定点的等⾼线(等位线)4,三元函数:三元函数的的图形是四维空间的⼀个点集. 所以画三元函数的⼀些等⾼线便于理解三元函数.例如:f(x,y,z) = 4Ln(x^2 + y^2 + z^2)可以画f(x,y,z) = 0 ,f(x,y,z)=1 .... 三维等位⾯图形。
Matlab与Mathematica在非线性拟合中的应用比较

( 02 , 0} 0 5 6 } O7 , 5} { . 5 3 ,{ . 8 ,{ .5 7 , { , 2 , { ., 2} 2 7 ,{ ., 8} 18 ) 1 8 ,{ , 7} 25 6 , 5 { , 8) 35 5 ,{ , 1 , { ., 0) 3 6 ,{ ., 8) 4 5 ) 4 5 5 , f , 1 ,f , 8 , { , 5) { , 8 , 5 4 } 6 3 ) 73 , 82 } { , 5} { 0 1 ,{ 1 1 , 9 2 , 1 , 8) 1 , 5} { 2 l , ( 3 1 , { 4 7} l , 2} 1 , 0) 1 , ,
时 间 (JH ,I ,
p = i Po d t] g Ls ll a t t a 就 可以输 出的带坐标 的散点 图。 当数 据 需手 动输 入 时 ,Mah maia te t 可 c 以 随 时 将 录 入 错 误 的 数 据 加 以 修 正 ,而 在 M alb 令 窗 口中 ,如 果 需 要修 正 数 据 , t 命 a 就 必 须 调 出 已输 入 过 的 数 据 再 加 以 修 改 , 查 找起 来 不  ̄ Mah maia 便 。作 图时 N t e tc 方 Maa 使用绘 图命令po tb l l t= ( ,Y 口 ) t , ,而 Mah mai 用Ls lt aa,两 种软件 绘 图 t e t a i P o[ t ] c t d 操 作都很 方便 。 其次 ,利 用软 件的 内建 函数对 此数据 进 行 非线性拟 合 。做 出比较 。 用Mal 的 内 建函数 对参 数求 解 ,可调 tb a 用 最小二乘拟 合 函 ̄l cret ,先 定义非 s uvf() q i 线性 函数t . 文件 : i i m n fnt n u co Y= f (,t i ua ) n Y = ( }x (a1 t *x (a ) ) a ) p一 (}) ep一 ( ) 3e ) 一 2 t 这 里a1 o,a ) p,a ) () L ( 为 为 2 ( 代表A,即 3 为y A e = ( Le ) - 。 在 命令窗 口中运 行以下 命令 : >> t= [ .5 .,0 7 ,1 .,2 0 2 ,O 5 .5 ,15 ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线性回归和非线性拟合
线性回归和非线性拟合都是根据随机观测的一些数据,按照最小二乘法的原理,得到要分析的量和与它相关的量之间近似的函数关系的过程。
此外,还要求对结果做显著性检验、区间估计、预测、模型的优劣讨论和改进等。
Mathematica中,使用函数Regress来进行线性回归分析,其使用格式和做曲线拟合的Fit函数是一样的:(如果你只想得到拟合的函数而不需要分析结果,可以使用Fit函数)
Regress[拟合数据,用于拟合的函数列表,变量]
下面是其常用的几种形式:
例:数学模型(姜启源),第294页,牙膏的销售量
1.输入数据
2.调入统计函数包,这是使用回归函数必须做的准备。
3.进行回归分析
4.根据选项RegressionReport输出参数的置信区间
关于结果分析和改进工作请参考书第297页~300页。
Mathematica中,使用函数NonlinearFit进行非线性拟合(在5.0版中,可以用内部函数FindFit代替),使用函数NonlinearRegress进行非线性回归分析,它们的使用格式是一样的,但NonlinearFit只
给出最优拟合函数,而NonlinearRegress还可以对结果进行分析,此外它还有和Regress函数一样的选项RegressionReport。
下面是它们的使用格式:
NonlinearFit[数据,拟合函数形式,变量表,参数表]
NonlinearRegress[数据,拟合函数形式,变量表,参数表]
例:数学模型(姜启源),第312页,酶促反应,混合模型的求解和分析
上机练习:
(1)数学模型(姜启源)第326页,第1题(答案:参见配套的习题解答)
(2)数学模型(姜启源)第330页,第4题(答案:参见配套的习题解答)
(3)2004年数学建模竞赛C题中,人一次性喝下含酒精Q
的啤酒后,假设血液中酒精的浓度与时间
的关系为:
()()
()
bt at
aQ
C t e e
V a b
--
=-
-
,这里V0=420百毫升,a,b为待定参数,一瓶啤酒含有的酒
精量为21700毫克。
试根据题目给出的数据拟合求出参数a,b,作出相应的图形比较拟合的结果,并计算血液中酒精的浓度什么时候达到最大值。
附:某人在短时间内喝下2瓶啤酒后,隔一定时间测量他的血液中酒精含量(毫克/百毫升),得到数据如下:
(答案:可参考我校获奖论文)。
