沪教版(上海)初中数学九年级第一学期 26.3 二次函数y=ax2+bx+c的图像与性质 教案
上海教育版数学九上26.3《二次函数y=ax2+bx+c的图像》(第4课时)ppt课件

2a
a,b同号,对称轴在y轴左侧; b=0,对称轴是y轴; a,b异号,对称轴在y轴右侧
6
练
习
1、已知函数y = ax2 +bx +c的图象如下图所示, 根据图象信息你能得到关于系数 a , b , c 的一 些什么结论?
y
-1
.
.
1
x
y
x o D -3
y
x
-3
9
小
结
开口方向
当a > 0时,抛物线开口向上 当a < 0时,抛物线开口向下 直线
b 4ac b 2 ( , ) 2a 4a
对称轴
顶点坐标
x =
b 2a
开口向上,顶点是最低点 开口向下,顶点是最高点
a>0,开口向上,a<0,开口向下 c<0,图象与y轴交点在x轴下方 c>0,图象与y轴交点在x轴上方 c =0,图象过原点 a,b同号,对称轴在y轴左侧; b=0,对称轴是y轴; a,b异号,对称轴在y轴右侧
4
思考与归纳
2 y ax bx c 的图象如图所示,则( 抛物线
)
A. a>0,b>0,c>0 C. a<0,b>0,c>0
B. a>0,b<0,c>0 D. a<0,b&
5
思考与归纳
⑴ a决定抛物线开口方向:a>0,开口向上 a<0,开口向下
⑵ c决定抛物线与y轴交点的位置: c<0,图象与y轴交点在x轴下方 c>0,图象与y轴交点在x轴上方 c =0,图象过原点
顶点坐标
a>0时,对称轴左侧部分是下降的,右侧部分是上升的 a<0时,对称轴左侧部分是上升的,右侧部分是下降的
沪教版(五四制)九上二次函数19=ax2+bx+c的图像

当a>0时,它的开口向__上_,顶点是抛物线的最_低__点; 当a<0时,它的开口_向__下,顶点是抛物线的最_高__点.
课堂练习
4.指出下列抛物线的开口方向、对称轴和顶点坐标.
函数
开口方向 对称轴 顶点坐标
y 2 x 1 2 1 2
y ax2 左右平移
y ax m2
上 下 平 移
y ax2 k
左右平移
上 下 平 移
y ax m2 k
(2)如果抛物线y=x2+ m +1的顶点是坐标轴的原点, 那么m的值是__m__=_-__1__.
(3)如果抛物线y=(x+m)2+m+3的对称轴是直线x=1,那 么它的顶点坐标是_(_1_,_2_)_.
课堂练习
5.填空: (4)如果抛物线y=m(x+1)2+m+1的顶点坐标是 (-1,-2),那么它的开口方向是__向__下____.
2
平移后 2.说出抛物线y=3(x- 移得到.
1 3
平移前 )2+4是由抛物线y=3x2怎样平
向右平移 1 个单位,再向上平移4个单位.
3
课堂练习
3.抛物线y=(x+2)2是由抛物线 y=(x+2)2-6怎 样平移得到.
向上平移6个单位.
新课学习
二次函数y=a(x+m)2+k的图像的直观特征
抛物线y=a (x+m ) 2+k(a、m、k是常数,a≠0)
(5)如果抛物线y=a(x+m)2+k的顶点坐标是 (3,2),这个图像是由抛物线y=-2x2平移得到,则这
沪科版九年级数学上册《二次函数y=ax2+bx+c的图象和性质》课件

1、“手和脑在一块干是创造教育的开始,手脑双全是创造教育的目的。” 2、一切真理要由学生自己获得,或由他们重新发现,至少由他们重建。 3、反思自我时展示了勇气,自我反思是一切思想的源泉。 4、好的教师是让学生发现真理,而不只是传授知识。 5、数学教学要“淡化形式,注重实质.
6、“教学的艺术不在于传授本领,而在于激励、唤醒、鼓舞”。2021年11月2021/11/82021/11/82021/11/811/8/2021 7、“教师必须懂得什么该讲,什么该留着不讲,不该讲的东西就好比是学生思维的器,马上使学生在思维中出现问题。”“观察是 思考和识记之母。”2021/11/82021/11/8November 8, 2021 8、普通的教师告诉学生做什么,称职的教师向学生解释怎么做,出色的教师示范给学生,最优秀的教师激励学生。 2021/11/82021/11/82021/11/82021/11/8
在同一坐标系中,画出函数:
y=- 1x2 y=- x12-1 y=- (x1+1)2-1的图象。
2
2
2
函数y=a(x-h)2+k的特点:
1、a>0时,开口向上;a<0时,开口向 下;
2、对称轴是直线x=h;
3、顶点坐标是(h,k).
你知道哪些地方用到了抛物线。
你知道哪些地方用到了抛物线。
你知道哪些地方用到了抛物线。
生活中的抛物线
生活中的抛物线
画出函数: y= x2 y=x2+1
y=x2-1的图象
❖ y=x2+1开口向上,对称 轴为y轴,顶点是(0、1)。
❖ y=x2-1开口向上,对称 轴为y轴,顶点是(0、-1)。
画 的图出象函数。y=-12 x2 y=- 12(x+1)2与y=- 12(x-1)2
2017秋上海教育版数学九上26.3《二次函数y=ax2 bx c的图像》(第1课时)ppt课件

左 单位
2
y (x 2)
26.3(1) 二次函数y=ax2+bx+c的图像
思
考
y (x 2) 2 抛物线的解析式是什么?
如果将抛物线
1 3个单位,所得的 2 向上平移
y
y
1 2 (x 2) 3 2 P
1 2 y (x 2) Q 2
o
y
1 2 x 2
x
试 一 试
怎样将抛物线 别得到下列抛物线
1 2 通过左右、上下二次平移,分 2
y x
1 2 y (x - 3) 2 2
1 2 y (x 3) - 2 2
1 2 y (x - 3) -4 2
思考与归纳
y ax
2当m>0,向左平移
当m<0,向右平移
y a( x m) 2 当k>0,向上平移 y a( x m) 2 k
练
习
1、与抛物线y=-4x2形状相同,顶点为(2,-3)的抛 物线解析式为 。 y=±4(x-2)2 -3
2、如果抛物线
1 y 的顶点坐标是( ( x h) 2 k-1,5), 2
.
5
则h=
,k= 1
练
习
3、已知二次函数图象顶点为(-1,-6),并且图象经过 点(0,5),求这个二次函数的解析式。
当x=-m时,最小值为k.
当x=-m时,最大值为k.
作
业
练习册:26.3(1)
小
结
抛物线 顶点坐标 对称轴 开口方向 增减性 最值
y=a(x+m)2+k (a>0) (- m,k) 直线x= - m 向上
沪教版(上海)初中数学九年级第一学期 26.3 二次函数y=ax2+bx+c的图像 课件课件ppt

20、不要相信普通的东西是有价值的。您必须为生活中的所有事物而奋斗。如果今天和昨天没有什么不同,那就快点改变自己。 7、要坚强,不要在悲伤中流泪,而要在擦掉眼泪后微笑并面对未来的生活。 8、如果您现在正走在一条似乎没有前途的曲折道路上,则必须走下去,因为只有在完成这条道路时,您才会知道想要什么。 15、朝着自己的目标奔跑,为什么不关心那些不幸的事情,只要您的信心不消失,就可以看到正确的方向,风适合步行,逆风更适合您飞行 ,您不应该害怕生活中的任何事情,只怕放弃。
3、利用对称性描点画图 .
课堂小结
学习感想说一说
1.这节课你学会了什么? 2.你认为有哪些要注意的地方? 3.你还有什么疑惑吗?
配方法的步骤:
• 一化(化二次项系数为1) • 二配(配常数项) • 三合(合成完全平方形式) • 四合并常数项.
注意:其中第2步----配常数项,具体方法是:在二次项系数为1的前
5、生命很短暂,没有必要太在乎生命,有些事情不了解,他们不了解;有些人无法猜测,他们不会猜测;一些理想不认为。生活不会因为您 的抱怨而改变;生活不会因为你的忧郁而改变。
24、做事的最佳状态是:不是故意的。不要刻意自我表达,不要刻意淡化名利;不故意迎合,也不故意自大;不要刻意追逐流行,也不刻意 出类拔萃。如果是这样,您不会感到疲倦,纠结或失望。
顶点2, 1
数无形时少直觉,形少数时难入微, 数形结合百般好,隔离分家万事休
变式训练,一题多解 1.指出下列函数的开口方向、对称轴和
顶点坐标:
1 y 1 xx 2
2 y 3x 1x 2
沪教版(上海)九年级第一学期《二次函数y=ax2+bx+c的图像(四)(公式法)》课件

b 2a
2
5
2
5 4
4ac b2 4a
42 7 52 4 2
81 8
∴抛物线的开口方向向上,顶点坐标是( 5 , 81),对称
48
轴是直线 x
5 4
,抛物线在直线 x
5左侧的部分是
4
上升的、右侧的部分是下降的.
‹# ›
课堂练习
二
‹# ›
‹# ›
‹# ›
‹# ›
26.3(3) 二次函数y=ax2+bx+c的图像
解:
y
2 3x2
5
x
2
2
a 3 0,b 5 , c 2
52
b 2a
2
2 3
5 12
4ac b2 4a
4
2
3
4 3
5
2
2
71 48
∴抛物线的开口方向向上,
顶点坐标是( 5 , 71) ,
12 对称轴是直线
48
x
5
12
.
(4) y 3x2 2x
解:a=3>0,b=2,c=0
对称轴是直线 x 3,
顶点坐标是 (3,12) .
(2) y 2x2 5x 2
解:a=2>0,b=-5,c=2
b 5 5 2a 2 2 4
4ac b2 4 2 2 52 9
4a
42
8
∴抛物线开口向上,
对称轴是直线 x 5 ,
顶点坐标是(
5
,
9
4 ).
48
‹# ›
课堂练习
(3) y 5 x 2 3x2
进门测
二次函数 y 2x2 4x 3图像的开口方向、对称 轴、对称顶点为?
沪教版(上海)初中数学九年级第一学期 26.3(2)二次函数y=ax2+bx+c的图像 教案
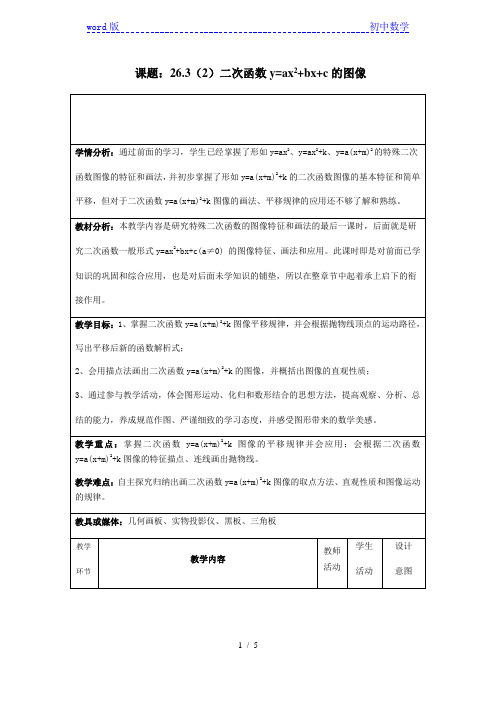
y=(x-1)2+4的图像。
解:此抛物线开口___,对称轴_________,顶点坐标___________。
x
…
…
y=(x-1)2+4
…
…
描点、连线 ,画出抛物线y=(x-1)2+4
思考:将抛物线y=(x-1)2-4进行怎样的图形运动可以和
抛物线y=(x-1)2+4重合?
课题:26.3(2)二次函数y=ax2+bx+c的图像
学情分析:通过前面的学习,学生已经掌握了形如y=ax2、y=ax2+k、y=a(x+m)2的特殊二次
函数图像的特征和画法,并初步掌握了形如y=a(x+m)2+k的二次函数图像的基本特征和简单
平移,但对于二次函数y=a(x+m)2+k图像的画法、平移规律的应用还不够了解和熟练。
板书
课题
利用
多媒
体教
学,
展示
图形
运动
的过
程
板演
作图
过程
强调
作图
要求
启发
学生
观察
思考
得出
结论
巡视
个别
辅导
展示
学生
作图
师生
共同
纠错
欣赏
点评
动画
演示
促进
理解
总结
独立
思考
口答
问题
观察
图像
变化过程,Fra bibliotek并解答
独立
完成
自主
归纳
观察
分析
师生
共同
归纳
沪教版数学九年级(上学期)一课一练及单元测试卷和参考答案

沪教版数学九年级上学期一课一练、单元测试卷和参考答案目录第二十四章相似三角形24.1放缩与相似形(1) 3 24.2 比例线段(1) 6 24.3三角形一边的平行线第一课时(1) 10 24.3三角形一边的平行线第二课时(1) 14 24.3三角形一边的平行线第三课时(1) 19 24.3三角形一边的平行线第四课时(1) 22 24.4相似三角形的判定第一课时(1) 25 24.4相似三角形的判定第二课时(1) 29 24.4相似三角形的判定第三课时(1) 33 24.4相似三角形的判定第四课时(1) 37 24.5相似三角形的性质第一课时(1) 43 24.5相似三角形的性质第二课时(1) 47 24.5相似三角形的性质第三课时(1) 52 24.6实数与向量相乘第一课时(1) 57 24.7向量的线性运算第一课时(1) 62 九年级(上)数学第二十四章相似三角形单元测试卷一 67 第二十五章锐角三角比25.1锐角三角比的意义(1) 72 25.2求锐角的三角比的值(1) 75 25.3 解直角三角形(1) 7925.4 解直角三角形的应用(1) 84 九年级(上)数学第二十五章锐角的三角比单元测试卷一 90 第二十六章二次函数26.1 二次函数的概念(1) 9426.2 特殊二次函数的图像第一课时(1) 98 26.2 特殊二次函数的图像第二课时(1) 102 26.2 特殊二次函数的图像第三课时(1) 106 26.3二次函数y=ax2+bx+c的图像第一课时(1) 111 26.3二次函数y=ax2+bx+c的图像第二课时(1) 116 26.3二次函数y=ax2+bx+c的图像第三课时(1) 121 九年级(上)数学第二十六章二次函数单元测试卷一 126 参考答案 132数学九年级上第二十四章相似三角形24.1放缩与相似形(1)一、选择题1下列各组图形中一定是相似三角形的是()A. 两个等腰三角形B. 两个直角三角形C. 一个角为30 的等腰三角形D. 两个等边三角形2下列各组图形中一定是相似多边形的是()A. 两个平行四边形B. 两个正方形C. 两个矩形D. 两个菱形3某两地的实际距离为3000米,画在地图上的距离是15厘米,则在地图上的距离与实际的距离之比是()A 1:200B 1:2000C 1:20 000D 1:200 0004. 下列不一定是相似形的是()A. 边数相同的正多边形B. 两个等腰直角三角形C. 两个圆D. 两个等腰三角形5. 下列给出的图形中,是相似形的是()A. 三角板的、外三角形B. 两孪生兄弟的照片C. 行书中的“中”楷书中的“中”D. 同一棵树上摘下的两片树叶6. 下列各组图形中,一定是相似多边形的是()A. 两个直角三角形B. 两个平行四边形C. 两个矩形D. 两个等边三角形7下列图形中,相似的有()①放大镜下的图片与原来图片;②幻灯的底片与投影在屏幕上的图像③天空中两朵白云的照片④用同一底片洗出的两大小不同的照片A. 4组B. 3组C. 2组D. 1组8. 对一个图形进行放缩时,下列说确的是()A. 图形中线段的长度与角的大小都保持不变B. 图形中线段的长度与角的大小都会改变C. 图形中线段的长度保持不变,角的大小可以改变D. 图形中线段的长度可以改变,角的大小都保持不变二、填空题9. ABC ∆与'''A B C ∆相似,则它们的对应角,对应边。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§26.3(4)二次函数2y ax bx c =++的图像与性质
【教学目标】
1、熟练掌握用配方法把二次函数的一般式转化为顶点式;
2、熟悉二次函数一般式的对称轴、顶点公式,并能运用公式解决相关问题;
3、熟悉二次函数的图像及性质,并能运用性质解决相关问题.
【重点与难点】
重点:会求二次函数(一般式)的顶点与对称轴(配方法或公式法).
难点:运用抛物线的性质解决相关问题.
【课型】习题课
【教学资源】几何画板课件 【教学日期】 2018 年 11 月 29日下午第2节
【教学过程】本节课共分五个环节:
第一环节:知识梳理;第二环节:巩固双基;第三环节:变式练习;第四环节:能力提升; 第五环节:课堂小结. 第一环节:知识梳理
1、二次函数)0(2≠++=a c bx ax y 的图像是一条 .
2、通过 ,可将一般式化为顶点式:222
424b ac b y ax bx c a x a a -⎛⎫=++=++ ⎪⎝⎭. 3、二次函数)0(2≠++=a c bx ax y 的对称轴是:直线x =-
,顶点坐标(-a
b 2,a b a
c 442-). 4、(1)当a > 0时,抛物线的开口 ,顶点是抛物线的最 点,抛物线在对称轴左侧部分是 ,
在对称轴右侧部分是 ;
(2)当a < 0时,抛物线的开口 ,顶点是抛物线的最 点,抛物线在对称轴左侧部分是 ,
在对称轴右侧部分是 .
第二环节:巩固双基
1、用配方法将二次函数化为顶点式,并指出它的开口方向、对称轴和顶点坐标.
(1)x x y 522-= (2)162
162--=x x y
2、(1)已知抛物线1)3(2++-+=n x n x y 经过坐标原点,则抛物线的顶点坐标是 .
(2)抛物线14
12-+=x x y 向 平移 个单位,再向 平移 个单位后, 与抛物线1412+=
x y 重合.
第三环节:变式练习
3、(1)已知抛物线3)5(2
12-+-+-=m x m x y 的顶点在y 轴上,求抛物线的顶点坐标;
(2)已知抛物线3)3(212-+-+-=m x m x y 的顶点在x 轴上,求抛物线的顶点坐标.
4、 (1)已知抛物线22-++=m x x y 的顶点在直线x y -=上,求m 的值;
(2)已知抛物线
22-++=m x x y 的顶点在第三象限,求m 的取值范围.
5、(1)已知抛物线122++-=x x y ,若y 随x 的增大而增大,则x 的取值范围是 .
(2)已知抛物线222++=mx x y ,当2>x 时y 的值随x 的增大而增大,则实数m .
第四环节:能力提升
6、已知二次函数)(x f y =的图像是开口向上的抛物线,)5(-f 、)1(-f 、)4(f 、)7(f 这四个函数值中有且
只有一个值不大于零,画图分析这样的抛物线的位置特征,并写出满足条件的一个函数解析式,你还能写出其他的解析式吗?
解:1、取4
1=a 分析: 对称轴:y 轴 对称轴:x 轴 对称轴:x=-1,x=4,x=-5,x=7 对称轴:任意
2、甲同学:3)2(2--=x y 的答案可以吗? 乙同学:10)2(2--=x y 的答案可以吗?
3、当1=a ,对称轴2=x 的条件下,顶点纵坐标的取值范围是什么?
解:4个点中只要关注最低点与次低点
设k x y +-=2)2(,满足条件⎩⎨⎧>-≤0)1(0)4(f f ⇒⎩
⎨⎧->-≤94k k 49-≤<-⇒k
第五环节:课堂小结
以巩固基础知识和基本技能为重点,在熟练配方的基础上,围绕二次函数的图像与性质展开一系列的变式练习,达到巩固知识、拓展能力的教学目标。
【回家作业】
1、练习册
2、堂堂练。
