信号与系统第七章1郑君里
信号与系统_郑君里_第三版_课件

2016/5/9
6
积分器:
R
C vo ( t )
微分器: C
vi(t)
vi(t)
R
vo ( t )
电视系统:
黑灰白 消息 变换器 发射机 信道 (空间) 接收机 变换器
黑灰 白 消息
(图像) (摄像机)
(显像管) (图像)
2016/5/9
7
1.2 信号分类和典型信号
1.2.1 信号的分类
对于各种信号,可以从不同角度进行分类。
2016/5/9
5
系统:一组相互有联系的事物并具有特定功能的整体。
系统可分为物理系统和非物理系统。如:电路系统、 通信系统、自动控制系统、机械系统、光学系统等属于 物理系统;而生物系统、政治体制系统、经济结构系统、 交通系统、气象系统等属于非物理系统 。 每个系统都有各自的数学模型。两个不同的系统可 能有相同的数学模型,甚至物理系统与非物理系统也可 能有相同的数学模型。将数学模型相同的系统称为相似 系统。
(t )
t
( t0 )d u (t t0 )
(1)
0 u(t) 1 0
25
u(t)与 (t ) 的关系:
t
2016/5/9
t
( )d u(t )
d u (t ) (t ) dt
t
( t0 )d u(t t0 )
t
d u (t t0 ) (t t0 ) dt
f (t ) (t ) f (0) (t )
f (t )
f (0)
(1)
(t )
(1)
f (0) (t )
《信号与系统》(郑君里)课后习题答案
(t )
2
非线性:设 r1 ( t ) = e1
( t ) 、 r2 ( t ) = e2 2 ( t ) ,
2 2 2 2
则⎡ ⎣ c1e1 ( t ) + c2 e2 ( t ) ⎤ ⎦ = c1 e1 ( t ) + c2 e2
2
( t ) + 2c1c2e1 ( t ) e2 ( t ) ≠ c1r1 ( t ) + c2 r2 ( t )
5
即 输 入 x1 ( t ) , x2 ( t ) 得 到 的 输 出 分 别 为 y1 ( t ) , y2 ( t ) , T ⎡ ⎣ x1 ( t ) ⎤ ⎦ = y1 ( t ) ,
T⎡ 。 ⎣ x2 ( t ) ⎤ ⎦ = y2 ( t ) ,则 T ⎡ ⎣ c1 x1 ( t ) + c2 x2 ( t ) ⎤ ⎦ = c1 y1 ( t ) + c2 y2 ( t ) ( c1 , c2 为常数)
解题过程:
(a-1)
(a-2)
(a-3)
4
(a-4)
(b) f ( t ) 为偶函数,故只有偶分量,为其本身
(c-1)
(c-2)
(c-3)
(c-4)
(d-1)
(d-2)
(d-3)
(d-4)
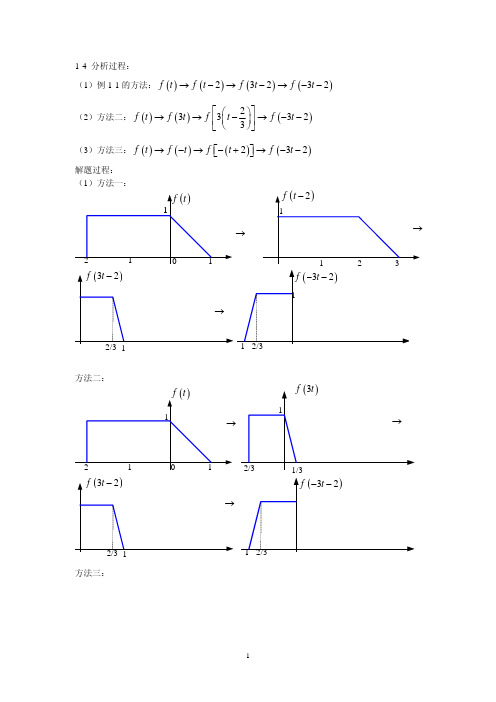
1-20 分析过程:本题为判断系统性质:线性、时不变性、因果性 (1)线性(Linearity) :基本含义为叠加性和均匀性
f (t )
1 1
f ( 3t )
→
→
-2
-1
0
1
-2/3
f ( 3t − 2 )
→
1/3
f ( −3t − 2 )
郑君里信号与系统课件总复习

第四章 拉普拉斯变换、 连续时间系统的s域分析
收敛域:实际上就是拉氏变换存在的条件;
lim f (t)eσt 0
t
σ σ0
三.一些常用函数的拉氏变换
1.阶跃函数
Lu( t )
2.指数函数
0 1
estd
t
1 est 1 s 0 s
L eα t eα testd t
eα st
奈奎斯特抽样间隔
16
重点: 1、傅里叶变换定义和存在条件 2、典型信号的傅里叶变换 3、傅里叶变换的性质 4、抽样定理
1、已知f ( t )的傅里叶变换为F( j ),求信号 f ( 2t 5 )的傅里叶变换
,
2、已知信号f ( t ) sin(1000 t ) 。 当对该信号取样时,试求能恢复原信号的最大抽样周期
t
f ( t ) ( t )dt f ( 0)u(t )
第一章
2、系统框图列微分方程
第二章 连续时间系统的时域分析
➢ 微分方程式的建立与求解
➢ 零输入响应与零状态响应 ➢ 冲激响应与阶跃响应
关系!
➢ 卷积及其性质(方便求零状态响应)
系统分析过程
列写方程: 根据元件约束,网络拓扑约束
整个 s 平面
0
0
0
0
第五章 掌握基本概念 ❖ 滤波器的类型
第七章 离散时间系统的时域分析
❖ 序列的概念、离散时间信号的运算
相加、相乘、序列移位、反褶、尺度倍乘、差分、累加
❖ 常系数线性差分方程的求解
迭代法 时域经典法:齐次解+特解 零输入响应+零状态响应
❖ 离散时间系统的冲激响应与阶跃响应
第四章
❖ 因果系统的s域判决条件:
信号与系统第七章1郑君里

xnT sinΩ0 nT 令 0 Ω0T,离散正弦信号
区别:
xn sin 0 n
连续 连续 连续域的正弦频率 离散域的频率
17
Ω0 ω0
单位 弧度 / 秒 单位 弧度
ω0 π,
7.复指数序列
xn e j0n cos 0 n j sin 0 n
8
1.单位样值信号
0, n 0 ( n) 1, n 0 0, n j 时移性 ( n j ) 1, n j
比例性 c ( n), c ( n j ) 抽样性 f ( n) ( n) f (0) ( n)
( n)
1
O
1
n
( n 1)
2.单位阶跃序列
1 u( n) 0
n0 n0
u( n) 1
1 O
1 23
n
u(n)可以看作是无数个单位样值之和:
u( n) ( n) ( n 1) ( n 2) ( n 3) (n k )
k 0
n与un是差和关系,不再是微 商关系。
x ( n)
1
1 O 1 2 3 4
n
13
5.单边指数序列
xn a n un
a n un
a 1
a n un
0a1
1
1
1
O
1
2
3
4
n
1 O
1
a n un
2
3
4
n
a n un
a 1
1 a 0
1 1 O 1 2
3
1 4
n
信号与系统-课件-郑君里

1.1 Signals
Signals are functions of independent variables that carry information. The independent variables can be continuous or discrete. The independent variables can be 1-D, 2-D, ••• , n-D. For this course: Focus on a single (1-D) independent variable which we call “time”. Continuous-Time signals: x(t), t-continuous values. Discrete-Time signals: x(n), n-integer values only.
School of Computer Science and Information
Examples
Electrical signals — voltages and currents in a circuit. Acoustic signals — audio or speech signals. Video signals — intensity variations in an image. Biological signals — sequence of bases in a gene.
School of Computer Science and Information
1.3 Types of Signals
1. Certain Signal and Random Signal
信号与系统(郑君里)复习要点

信号与系统复习书中最重要的三大变换几乎都有。
第一章 信号与系统 1、信号的分类 ①连续信号和离散信号 ②周期信号和非周期信号 连续周期信号f (t )满足f (t ) = f (t + m T ), 离散周期信号f(k )满足f (k ) = f (k + m N ),m = 0,±1,±2,…两个周期信号x(t),y(t)的周期分别为T 1和T 2,若其周期之比T 1/T 2为有理数,则其和信号x(t)+y(t)仍然是周期信号,其周期为T 1和T 2的最小公倍数。
③能量信号和功率信号 ④因果信号和反因果信号 2、信号的基本运算(+ - × ÷) 2.1信号的(+ - × ÷)2.2信号的时间变换运算 (反转、平移和尺度变换) 3、奇异信号3.1 单位冲激函数的性质f (t ) δ(t ) = f (0) δ(t ) , f (t ) δ(t –a) = f (a) δ(t –a)例: 3.2序列δ(k )和ε(k )f (k )δ(k ) = f (0)δ(k ) f (k )δ(k –k 0) = f (k 0)δ(k –k 0)4、系统的分类与性质?d )()4sin(91=-⎰-t t t δπ)0()()(f k k f k =∑∞-∞=δ4.1连续系统和离散系统4.2 动态系统与即时系统4.3 线性系统与非线性系统①线性性质T[a f (·)] = a T[ f (·)](齐次性)T[ f1(·)+ f2(·)] = T[ f1(·)]+T[ f2(·)] (可加性)②当动态系统满足下列三个条件时该系统为线性系统:y(·) = y f(·) + y x(·) = T[{ f(·) }, {0}]+ T[ {0},{x(0)}] (可分解性)T[{a f(·) }, {0}] = a T[{ f(·) }, {0}]T[{f1(t) + f2(t) }, {0}] = T[{ f1(·) }, {0}] + T[{ f2(·) }, {0}](零状态线性) T[{0},{a x1(0) +b x2(0)} ]= aT[{0},{x1(0)}] +bT[{0},{x2(0)}](零输入线性) 4.4时不变系统与时变系统T[{0},f(t -t d)] = y f(t -t d)(时不变性质)直观判断方法:若f (·)前出现变系数,或有反转、展缩变换,则系统为时变系统。
郑君里信号与系统课件

T1 2 T 1 2
f ( t )dt
余弦分量 系数 正弦分量 系数
T1 2 T 1 2
f ( t ) cos(n1t )dt
2 bn T1
T1 2 T 1 2
f ( t ) sin( n1t )dt
注意!
傅立叶级数与傅立叶系数的联系与区别
指数形式傅立叶级数的傅里叶系数
尺度变换、初值、终值
卷积特性 拉氏逆变换
部分分式展开法(求系数)
系统函数H(s)
定义(两种定义方式)
求解(依据两种定义方式)
第四章 拉普拉斯变换、 连续时间系统的s域分析
收敛域:实际上就是拉氏变换存在的条件;
σ t
lim f (t ) e
t
0
σ σ0
三.一些常用函数的拉氏变换
t n st n n1 st e t e dt s 0 s 0
n n1 st t e dt s 0 n n 1 n 所以 L t L t s n1
Lt t e d t
st 0
1 1 st 1 e s2 s s 0 n2 2 2 1 2 2 L t Lt 2 3 s s s s n3 3 2 3 2 6 3 Lt Lt 3 4 s s s s
1 sin( t ) (e jt e jt ) 2j 1 cos(t ) (e jt e jt ) 2
推出 公式
第一章 绪论
关于冲激信号
(at )
1 (t ) a
尺度变换特性
(t ) f (t ) f (0) (t )
信号与系统郑君里课件

04
信号的频域分析
傅里叶变换的定义与性质
傅里叶变换的性质
线性、时移、频移、共轭、对称等性质,这 些性质在信号处理中有着广泛的应用。
傅里叶变换
将时间域信号转换为频域信号的数学工具。
傅里叶变换的逆变换
将频域信号还原为时间域信号的过程。
频域表示与频谱分析
01
频域表示
通过傅里叶变换,将信号从时间 域转换到频域,用频率作为自变 量表示信号特性。
系统。
信号与系统的重要性及应用领域
总结词
信号与系统是信息传输和处理的基础,广泛应用于通 信、控制、图像处理等领域。
详细描述
信号与系统是信息科学和技术领域的基础学科,是研究 信息传输和处理的基本理论和方法。在通信领域中,信 号与系统理论用于研究信号的调制解调、频谱分析和信 道容量等问题;在控制领域中,信号与系统理论用于研 究系统的稳定性、时域和频域分析等问题;在图像处理 领域中,信号与系统理论用于研究图像的压缩编码、滤 波和增强等问题。此外,信号与系统理论还在雷达、声 呐、生物医学工程等领域得到广泛应用。
02
信号的时域分析
信号的时域表示
信号的分类
根据不同的特性,信号可以分为连续信号和离散 信号、确定性信号和随机信号等。
信号的时域表示
信号在时间轴上的取值表示,可以是连续的波形 或离散的序列。
信号的基本属性
幅度、频率、相位等。
信号的时域运算
信号的延迟和提前。
信号的微分、积分等时域 变换。
信号的加法、减法、乘法 等基本运算。
系统的频域响应
线性时不变系统的频域响应
01
描述系统对不同频率输入信号的输出响应,包括幅度响应和相
位响应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( n) u(n) u( n 1)
3.矩形序列
1 RN ( n ) 0
RN ( n )
0 n N 1 n 0, n N
1
1 o 1 2 3
N 1 n
与un的关系:RN (n) u(n) u(n N )
12
4.斜变序列
x( n) nu( n)
xnT sinΩ0 nT 令 0 Ω0T,离散正弦信号
区别:
xn sin 0 n
连续 连续 连续域的正弦频率 离散域的频率
17
Ω0 ω0
单位 弧度 / 秒 单位 弧度
ω0 π,
7.复指数序列
xn e j0n cos 0 n j sin 0 n
第七章离散时间系统的时域分析
离散时间信号、离散时间系统
f tk
离散时间信号: 时间变量是离散的,函数 只在某些规定的时刻有确定的 值,在其他时间没有定义。
t 2 t 1 o
t1 t 2 t 3
tk
离散信号:可以由模拟信号抽样而得,也可以由实际 系统生成。
离散时间系统:系统的输入、输出都是离散的时间信 号。如数字计算机。
1
系统分析
连续时间系统——微分方程描述
经典法:齐次解 特解 时域分析 零输入响应 零状态响应 变换域分析: 拉氏变换法
离散时间系统——差分方程描述 差分方程的解法与微分方程类似
经典法:齐次解 特解 时域分析 零输入响应 零状态响应 变换域分析: z变换法
1.相加: z(n) x(n) y(n) 2.相乘: z(n) x(n) y(n) z( n) ax( n) 3.乘系数: 4.移位: z( n) x( n m ) z ( n) x ( n m )
x 1 x 0
x n x 3
3
右移位 左移位
xn sinnω0 余弦序列:xn cosn 0
sinnω0 1 O 1 5 10 n sin 0 t
6.正弦序列
1
0 : 正弦序列的频率 , 序列值依次周期性重复 的速率。
离散正弦序列 xn sin 0 n 是周期序列应满足
xn N xn N称为序列的周期,为任意正整数。
x 2n
O
6
n
6 5 4 3 2 1
n x 2
4
2
O
1 2 3 4 5 6
n
O
1 2 3 4 5 6 7 8 9 10
12
21 n
例3:设N=10,说明正弦序列的包络线每隔10个样值重 复一次,周期为10。
2π 2π ω0 0.2π N 10
表示相邻两个序列值间 的弧度数为 0.2π。
15
2π 当 0 = , 则序列每10个重复一次正弦包络的 数值。 10
正弦序列周期性的判别
①
2π
N,N是正整数 0 2π sin 0 n N sin 0 n sin 0 n 2π sin 0 n 0 正弦序列是周期的
一.离散信号的表示方法
xt xnT 等间隔T xn n 0,1,2,
数字序列 如 0.9, 0.8,0.3,0.1 n 0 有规则的, 可以用函数表示 : xn 波形表示 : 线段的长短表示各序列 值的大小
2.单位阶跃序列
1 u( n) 0
n0 n0
u( n) 1
1 O
1 23
n
u(n)可以看作是无数个单位样值之和:
u( n) ( n) ( n 1) ( n 2) ( n 3) (n k )
k 0
n与un是差和关系,不再是微 商关系。
x ( n)
1
1 O 1 2 3 4
n
13
5.单边指数序列
xn a n un
a n un
a 1
a n un
0a1
1
1
1
O
1
2
3
4
n
1 O
1
a n un
2
3
4
n
a n un
a 1
1 a 0
1 1 O 1 2
3
1 4
n
1 O
1
2
3
4
n
14
7.累加: z( n)
k
x( k )
8.重排(压缩、扩展):
n x n x an , 或 x n x a 注意:有时需去除某些点或补足相应的零值。
9.序列的能量 E
n
x ( n)
n
2
7
三.常用离散信号
•单位样值信号 •单位阶跃序列 •矩形序列 •斜变序列 •单边指数序列 •正弦序列 •复指数序列
2
本章内容
•离散时间信号及其描述、运算; •离散时间系统的数学模型——差分方程; •线性差分方程的时域解法; •离散时间系统的单位样值响应; •离散卷积。
学习方法
注意离散系统与连续系统分析方法上的联系、 区别、对比,与连续系统有并行的相似性。和前几 章对照,温故而知新。
3
第二节离散时间信号--序列
x n
3 4 5
1 2
9 10 11 6 7 8
22
n
一个周期
23
例5:信号xn sin0.4n是否为周期信号?
0 0.4
2π
0
5π是无理数 所以为非周期的序列
24
复序列用极坐标表示:
x n x n e
x n 1
jarg x n
复指数序列:
ቤተ መጻሕፍቲ ባይዱ
arg xn 0 n
18
数字角频率(离散域的频率)的取值
数字频率 0可以连续变化,
但0只能在 π ,π 范围内取值。 正弦函数本身周期为 2π , 0为抽样值的数字频率间隔 的弧度数,其数值不会超过 2π 。
ω0 反映每个序列值出现的速 率,ω0小,两个序列值 间弧度 小。
sin nω0 1
o1
sin Ω0 t 5
10 n
22
1
例4
4π 已知: sin n , 求其周期。 11 4π 2π 11 11 N ω0 ,则有: 2π 11 ω0 4π 2 m
所以N 11,即周期为11。( 2π 中有5.5个ω0 )
序列形式: x ( n ) ,0,0, 1 ,2,4,8, n 0
x n
波形:
2
4
1
O
2
2
1
1
n
20
例2
x n
6 5 4 3 2 1
已知x ( n)波形,请画出 n x ( 2n), x 波形。 2
1 2 3 4 5 6
●数字频率——抽样间隔的关系应满足Nyquist抽样率
0 Ω0TS 2π
TS为抽样间隔时间,s为抽样角频率,
0 π 可以取负值,所以0 π ,π
因为 S 2Ω0 , 所以0 π
19
S
Ω0
2 n , n 0 试写出其序列形式并画出波形。 例1 x ( n) 0, n 0
1
O
1
n
注意: ( t )用面积 强度表示, t 0,幅度为 ;
(n )在n 0取有限值为1不是面积 。
9
利用单位样值信号表示任意序列
x ( n)
m
x(m ) (n m )
f n
1.5
1
2 1
3
o
3
4
n
f n 1,1.5,0,3,0,0, n 1 1.5 n 3 n 2 n 0 10
x n 1 x 0
x 1
x 1
x 1
2 1 o 1
3
x 3
4
n
1 o
1 2
n
6
x 2
x 2
5.倒置: z(n) x( n) 6.差分: 前向差分:x( n) x( n 1) x( n)
后向差分:x( n) x( n) x( n 1)
2π
0 找不到满足 xn N xn的N值 ,为非周期的
16
离散信号 sinn 0 与连续信号 sin0 t 的关系与区别。
2 f t sin2πf 0 t sinΩ0 t Ω0 T 离散点(时刻)nT上的正弦值
8
1.单位样值信号
0, n 0 ( n) 1, n 0 0, n j 时移性 ( n j ) 1, n j
比例性 c ( n), c ( n j ) 抽样性 f ( n) ( n) f (0) ( n)
( n)
1
O
1
n
( n 1)
xn与xn概念上有区别,但为了书写方便,常以 xn
表示整个序列,在应 用场合一般不会混 淆。
4
序列的三种形式
单边序列: n 0;
x ( n)
双边序列: n ;
O
n x ( n)
O
n
x ( n)
有限长序列: n1 n n2;
O
n1
n2
5
n
二.离散信号的运算
N N , 为有理数 ② 0 m m 2π sin 0 n N sin 0 n m sin 0 n m 2π sin 0 n 0 2π sin 0 n仍为周期的 周期:N m 0 2π ③ 为无理数
