信号与系统—第七章习题讲解
合集下载
信号与系统王明泉第七章习题解答
（1）当，始终为负，收敛域为，为最大收敛半径； （2）当，可分解为两项级数的和，第一项为z的正幂次级数，根据 阿贝尔定理,其收敛域为，为最大收敛半径；第二项为有限长序列，其 收敛域为；取其交集，该左边序列的收敛域为。 4．双边序列 双边序列指为任意值时,皆有值的序列，即左边序列和右边序列之 和。其变换： 双边序列的收敛域为一环形区域。 下表列出了序列的形式与变换收敛域的关系。
（1） （2） （3） （4） 解：（1） 对差分方程两边取单边Z变换， 解：（2） 解：（3） 解：（4） 7.9分别求下列差分方程的系统函数、系统频率响应函数和单位样值响 应函数，并画出系统函数的零极点图和系统框图。 （1） （2） （3） （4） 解：（1） 系统函数，极点： 单位样值响应 频率响应 系统框图如图（1）所示，零极点图如图（a）所示。 解：（2） 系统函数，极点：，零点： 单位样值响应 频率响应 系统框图如图（2）所示，零极点图如图（b）所示。 解：（3） 系统函数 极点：，零点： 单位样值响应 频率响应 系统框图如图（3）所示，零极点图如图（c）所示。 解：（4） 系统函数 极点：，零点： 单位样值响应 频率响应 系统框图如图（4）所示，零极点图如图（d）所示。
7.2 本章重点
（1）z变换（定义、收敛域、性质、反变换、应用）； （2）z域分析（求解分析系统）； （3）系统的频率响应函数。
7.3 本章的知识结构 7.4 本章的内容摘要
7.4.1 Z变换
（1）定义
表示为：。
（2）收敛域
1.有限长序列 （1）当时，始终为正，收敛条件为； （2）当时，始终为负，收敛条件为； （3）当时，既取正值，又取负值，收敛条件为。 2.右边序列 （1）当时，始终为正，由阿贝尔定理可知，其收敛域为，为最小 收敛半径； （2）当时，分解为两项级数的和，第一项为有限长序列，其收敛 域为；第二项为z的负幂次级数，由阿贝尔定理可知，其收敛域为；取 其交集得到该右边序列的收敛域为。 3．左边序列
信号与系统第七章课后答案
第 7 章习题答案
7-1 分别绘出下列各序列的图形。 （2）x[n] 2n u[n] （3）x[n] (1/ 2)n u[n] （4）x[n] (2) n u[ n] （1）x[n] (1/ 2)n u[n] 解：
x[ n ]
1
x[n]
1
0 1 2 (1) 3 4
n
0
1
2 3 (2)
x[n]
1
x[n]
-4
-3
-2 (1)
-1
0
n
0
1
2 (2)
3
4
n
x[n]
-4 1 0 1 2 3 4 -3 -2 -1 0
x[n] n
-1
n
(4)
(3)
7-3
分别绘出下列各序列的图形。 （2） x[n] cos
n 10 5
n （1） x[n] sin 5
1 z2 X (z) ( 1 1 2 z 1 )( 1 2 z 1 ) ( z 1 2 )( z 2 ) X (z) z 1 4 z ( z 1 2 )( z 2 ) 3( z 1 2 ) 3( z 2 )
X (z)
z 4z 3( z 1 2 ) 3 ( z 2 )
N
)
由于 x[n] 、 h[n] 均为因果序列，因此 y[n] 亦为因果序列，根据移位性质可求得
y [ n ] Z 1 [Y ( z )]
1 1 (1 a n 1 ) u [ n ] (1 a n 1 N ) u [ n N ] 1 a 1 a
7-24 计算下列序列的傅里叶变换。
(2)
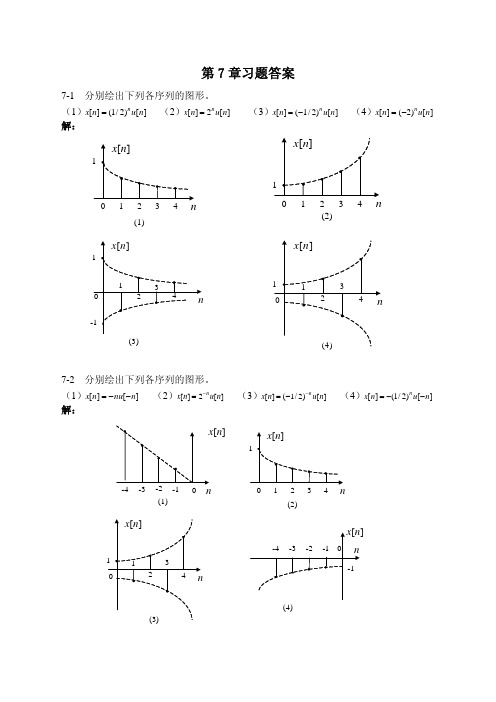
7-1 分别绘出下列各序列的图形。 （2）x[n] 2n u[n] （3）x[n] (1/ 2)n u[n] （4）x[n] (2) n u[ n] （1）x[n] (1/ 2)n u[n] 解：
x[ n ]
1
x[n]
1
0 1 2 (1) 3 4
n
0
1
2 3 (2)
x[n]
1
x[n]
-4
-3
-2 (1)
-1
0
n
0
1
2 (2)
3
4
n
x[n]
-4 1 0 1 2 3 4 -3 -2 -1 0
x[n] n
-1
n
(4)
(3)
7-3
分别绘出下列各序列的图形。 （2） x[n] cos
n 10 5
n （1） x[n] sin 5
1 z2 X (z) ( 1 1 2 z 1 )( 1 2 z 1 ) ( z 1 2 )( z 2 ) X (z) z 1 4 z ( z 1 2 )( z 2 ) 3( z 1 2 ) 3( z 2 )
X (z)
z 4z 3( z 1 2 ) 3 ( z 2 )
N
)
由于 x[n] 、 h[n] 均为因果序列，因此 y[n] 亦为因果序列，根据移位性质可求得
y [ n ] Z 1 [Y ( z )]
1 1 (1 a n 1 ) u [ n ] (1 a n 1 N ) u [ n N ] 1 a 1 a
7-24 计算下列序列的傅里叶变换。
(2)
信号与系统第七、八章课后习题
N k
当
2
2．线性时不变离散时间系统 ①线性 线性=叠加性+均匀性（齐次性）
c1 x1 (n) c2 x2 (n)
系统
c1 y1 (n) c2 y2 (n)
②时不变
x(n N )
系统
y (n N )
x ( n)
1 E
y ( n)
y ( n)
a
ay(n)
单位延时
1 T D z （ ）
已知激励初始状态y(-1)=0,y(-2)=1/2, fk=2ku(k),求系统 的零输入响应,零状态响应和全响应. 解: (1) 零输入响应 根据定义,零输入响应满足方程:
yx (k ) 3 yx (k 1) 2 yx (k 2) 0
其初始状态
1 yx (1) y (1) 0, yx 2 y 2 2
x(n)(n n0 ) x(n0 )(n n0 )
n
x(n)(n) x(0) (n) x(0)
n
n
x(n)(n n ) x(n ) (n n ) x(n )
0 0 n 0 0
x ( n)
k k 零状态响应
2 1 k k k (1) (2) (2) , k 0 3 3
离散时间系统的单位样值响应
(n)
零状态系统
h( n)
单位样值响应h(n)是系统在零状态时，由单位样值信 号作用之下产生的响应。因此，它是一个零状态响应。
同样，单位样值信号δ(n)仅在n=0时刻等于1，其它时 刻δ(n)=0，因此系统在n>0时的响应是零输入响应。
信号与系统教程习题解析(前七章)
3-19 一线性时不变 变系统，在 在某起始状态 态下，已知 知当输入f t 响应 应y t 3e ε t ；当 当输入f t ε t 时，全响应 时 y t e 系统 统的冲激响应h t 。 解 因为零状态响应 应 ε t → s t , 故有 有 y t y t 从而 而有 y t
10
8
3-10 试用算子法求 求下列系统 的冲激响应 应h t 。 a y 解 t 3y t 2y t p 从而 而有 H p 利用 用公式(3-3 31) K 可得 得K 于是 是 H p
5f t 3p 2 y t
7f 7 t 5p 7 f t K p 1 p K 2
d y t
试判断该系统是否为线性时不变系统？ 解
(a) 线性；(b) 线性时不变；(c) 线性时变；(d) 非线性时不变。
1-7 若有线性时不变系统的方程为 y′ t 若在非零f t 作用下其响应y t y′ t 的响应。 解 因为f t ↔ y t 1 e ，由线性关系，则 2 1 e e e 2 e e 1 ay t 2f t f t f′ t
i
0 ⇒ u 0
du dt 2V
u R C
i C
i 0 1A 1 u 0 1 R C
2 V
1 1V
3-5 设有 有一阶系统方程 y t 因方 方程的特征根 根λ δ t 时，则冲激 时 响应 h t g t ∗ δ t 3e
3 3y t 3， 故有 g t
f t
f t
试求 求其冲激响应 h t 和阶 阶跃响应 s t 。 解 当f t e ε t g t ε t
解
因为 t , |t| f t τ 0, |t| t e τ j2 τ
为奇 奇数，故 F ω f t e dt dt tsin nωtdt
信号与系统第七章课后习题答案
k 1
z
1
k
1 z 1 z
0 z
F( z )
k 1
f (k )z k
k
[(k 1) (k 2)]z k z2 z 1 z
k 1
z k z 1 z 1
例 7.1- 2 已知无限长因果序列f(k)=akε(k)。求f(k)
d d k f ( k ) ( z ) ( z ) F ( z ) z dz dz
d d d z k f ( k ) ( z ) z F ( z ) dz dz dz
|a|<|z|<|b|
Im[z]
Im[z] |a |
Im[z]
|a | o Re[z] o Re[z] o
|a|
Re[z] |b |
(a)
(b)
(c)
图 7.1-1 例7.1-2、例7.1-3、例7.1-4图
7.1.3 常用序列的双边Z变换
(1) f (k ) (k )。
F ( z)
k
例 7.2-3 已知
1 k 1 f (k ) 3 (k 1), 2
k
求f(k)的双边Z变换及其收敛域。 解 令f1(k)=3k+1ε(k+1)，则有
1 f ( k ) f1 ( k ) 2
z z2 由于 F1 ( z ) Z [ f1 (k )] z z3 z3
k
(k ) z k 1
（2） f1 (k ) (k m), f 2 (k ) (k m), m为正整数.
信号与线性系统分析(吴大正第四版)第七章习题答案
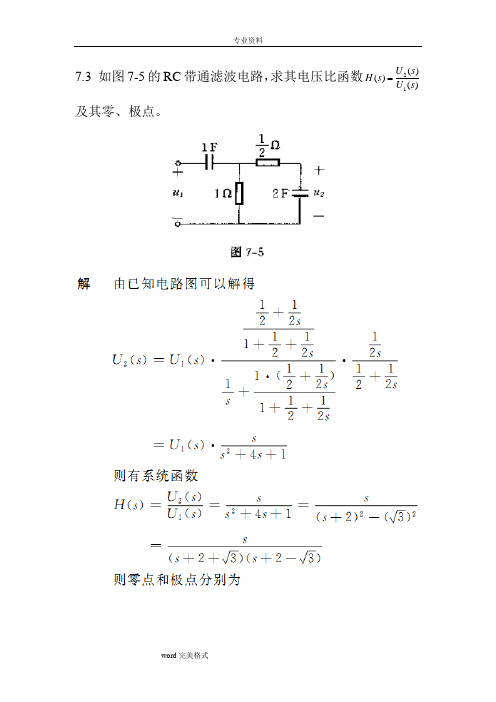
7.3 如图7-5的RC 带通滤波电路，求其电压比函数)()()(12s U s U s H 及其零、极点。
7.7 连续系统a 和b ，其系统函数)(s H 的零点、极点分布如图7-12所示，且已知当∞→s 时，1)(=∞H 。
（1）求出系统函数)(s H 的表达式。
（2）写出幅频响应)(ωj H 的表达式。
7.10 图7-17所示电路的输入阻抗函数)()()(11s I s U s Z =的零点在-2，极点在31j ±-，且21)0(=Z ，求R 、L 、C 的值。
7.14 如图7-27所示的离散系统，已知其系统函数的零点在2，极点在-0.6，求各系数a，b。
7.18 图7-29所示连续系统的系数如下，判断该系统是否稳定。
（1）3,210==a a ； （2）3,210-=-=a a ； （3）3,210-==a a 。
7.19 图7-30所示离散系统的系数如下，判断该系统是否稳定。
（1）1,2110-==a a ； （2）1,2110==a a ；（3）1,2110=-=a a 。
7.20 图7-31所示为反馈系统，已知44)(2++=s s ss G ，K 为常数。
为使系统稳定，试确定K 值的范围。
7.26 已知某离散系统的差分方程为)1()2()1(5.1)(-=---+k f k y k y k y（1） 若该系统为因果系统，求系统的单位序列响应h(k)。
（2） 若该系统为稳定系统，求系统的单位序列响应h(k)，并计算输入)()5.0()(k k f k ε-=时的零状态响应)(k y zs 。
7.28 求图7-36所示连续系统的系统函数)(sH。
7.30 画出图7-40所示的信号流图，求出其系统函数)(sH。
解(a)由s域系统框图可得系统的信号流图如图7-41(a)。
流图中有一个回路。
其增益为(b)由s 域系统框图可得系统的信号流图如图7-41(b)。
流图中有一个回路。
信号与系统教程习题解析(前七章)
题 4-1(a) 图
解
对于 于周期锯齿波 波信号，在 在周期( 0，T )内可表示 示为 At A f t t T A T T a 1 T f t dt d 1 T At T A dt A T t 2T t A 2 0
∵ω T 2 T 2A 2 T b 2 T
2π, 2 ∴
sinnω tdt t 2 2A T
《信 信号与系 系统教程 程》习题 题解析
第1 章 导论 导
1-1 题 1-1 图示信号中， 图 哪些是连续 续信号？哪 哪些是离散信 信号？哪些 些是周期信号 号？ 哪些 些是非周期 期信号？哪些 些是有始信 信号？
题 1-1 图
解
图(a a)、(c)、( (d)为连续信 信号；(b)为 为离散信号 号；(d)为周 周期信号；其 其余
(a)和(b)的波形如图 p2-1 所示。
2
图 p2-1
2-2 试用 用阶跃函数的组合表示 示题 2-2 图所 所示信号。 解 (a) f t (b) f t ε t ε t 2ε t ε t 1 T ε t ε t 2 2T T
题 2-2 图
2-3 如题 题 2-3 图所示 示f t ，试画 画出如下信 信号的波形。 。 (a) f (b) f t (c) f t (d) f 2t (e) f t/2 (f) f 2t 2
cosn nω tdt A 2A T
a
f t cosnω ω tdt tsinnω ω t nω f t sinnω ω tdt
tcosn nω tdt
cosnω ω tdt
sinnω t dt nω 2 2A T
0 2A A T
tsinn nω tdt
sinnω tdt
信号与系统—第七章习题讲解PPT课件
(1)x(n),h(n),见题图731(a) (2)x(n),h(n),见题图731(b)
(3)x(n)anu(n) 0<a<1;h(n)nu(n) 0<<1;a (4)x(n)u(n);h(n)(n2)(n3)
解 ：(1)由 图7－3（1 a） 可 知 ： x(n) (n) 2 (n 1) (n 2) h(n) (n) (n 1) (n 2) y(n) x(n)* h(n) [ (n) 2 (n 1) (n 2)] *[ (n) (n 1) (n 2)] (n) (n 1) (n 2) 2 (n 1) 2 (n 2) (n 3) (n 2) 2 (n 3) (n 4) (n) 3 (n 1) 4 (n 2) 3 (n 3) (n 4)
解 ： (3) (n 4);非 因 果 ， 稳 定 (5) u(3 n); 非 因 果 ， 不 稳 定 (7) 3n u ( n);非 因 果 ， 稳 定 (9) 0.5n u (n); 因 果 ， 稳 定
7 30对 应 于 线 性 时 不 变 系 统 ： (1)已 知 激 励 为 单 位 阶 跃 信 号 之 零 状 态 响 应 （ 阶 跃 响 应 ） 是 g (n),试 求 冲 击 响 应 h(n); ( 2 )已 知 冲 激 响 应 h ( n )， 试 求 阶 跃 响 应 g ( n )。
(2)单位阶跃信号u(n)可表示为：u(n)(nk) k0
由系统的线性时不变特性可得对(nk)的响应为
h(nk)。故阶跃响应g(n)h(nk)。 k0
731 以 下 各 序 列 中 ， x(n)是 系 统 的 激 励 函 数 ， h(n)是 线 性 时 不 变 系 统 的 单 位 样 值 响 应 。 分 别 求 出 各 y(n),画 出 y(n) 图 形 （ 用 卷 积 方 法 ） 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
7
8
77 8
如 果 3 N 是 2 的 整 数 倍 ， 则 由 余 弦 函 数 的 性 质 有 7
x ( n N ) x ( n )， 显 然 ， 满 足 此 条 件 的 最 小 整 数 值
为 N 14， 故 x (n )为 周 期 序 列 ， 其 周 期 为 14。
j( n )
(2)x(n) e 8
(1)x(n)(n);
(2)x(n)u(n)
解：由图可得系统差分方程为
y(n) x(n) 1 y(n 1) 3
(1) x ( n ) ( n ) 根 据 系 统 差 分 方 程 及 边 界 条 件 y(1) 0进 行 迭 代 求 解 ：
y(0) x(0) 1 y(1) 1 3
y (1) x (1) 1 y (0 ) 1
Байду номын сангаас
齐次解：y(n) (C1nC2)(1)n
由y(0)
y(1)
1C(2C11 C2)
1CC12
2 1
y(n) (2n1)(1)n
7 2 8以 下 各 序 列 是 系 统 的 单 位 样 值 响 应 h ( n ), 试 分 别 讨论各系统的因果性与稳定性。 (3) (n 4); (5) u(3 n); (7) 3n u ( n); (9) 0.5n u (n)
试确定其周期。
(1) x ( n )
A cos( 3
n
)；( 2 ) x ( n )
j(n )
e8
78
解 ： 如 果 对 于 整 数 N , 有 x ( n N ) x ( n )， 则 x ( n )是 周 期 序 列 。
由 于 x(n N ) A cos[ 3 (n N ) ] A cos[ 3 n 3 N ]
(2)单位阶跃信号u(n)可表示为：u(n)(nk) k0
由系统的线性时不变特性可得对(nk)的响应为
h(nk)。故阶跃响应g(n)h(nk)。 k0
731 以 下 各 序 列 中 ， x(n)是 系 统 的 激 励 函 数 ， h(n)是 线 性 时 不 变 系 统 的 单 位 样 值 响 应 。 分 别 求 出 各 y(n),画 出 y(n) 图 形 （ 用 卷 积 方 法 ） 。
解：由于x(n
N)
e
j[(
1(nN 8
)
]
j( n ) j N
e 8 .e 8
jN
x(n)e 8
若x(n N)
x(n)，则要求e
j
N 8
1，即 N
2k,为无理数，
8
故不存在满足此式的整数N, k，所以x(n)不是周期序列。
7－5列出题图7－5所示系统的差分方程，已知边界条件 y(1)0。分别求以下输入序列时的输出y(n),并绘出其 图形（用逐次迭代方法求）
3
3
y ( 2 ) x ( 2 ) 1 y (1) ( 1 ) 2
3
3
........
y(n) (1 )nu(n) 3nu(n) 3
(2)x(n) u(n)
y (0 )
x(0)
1 3
y ( 1)
1
30 30
y (1)
x (1)
1 3
y (0 )
1
1 3
30 31 31
y(2)
x(2)
解 ： ( 1 ) 单 位 激 励 信 号 （ n） 可 表 示 为 （ n） u ( n ) u ( n 1) 系 统 对 u ( n )的 响 应 是 g ( n )， 又 由 系 统 的 线 性 时 不 变 特 性 可 得 对 u ( n 1)的 响 应 是 g ( n 1)， 故 系 统 的 冲 激 响 应 为 ： （h n） g ( n ) g ( n 1)
(1)x(n),h(n),见题图731(a) (2)x(n),h(n),见题图731(b)
(3)x(n)anu(n) 0<a<1;h(n)nu(n) 0<<1;a (4)x(n)u(n);h(n)(n2)(n3)
解 ：(1)由 图7－3（1 a） 可 知 ： x(n) (n) 2 (n 1) (n 2) h(n) (n) (n 1) (n 2) y(n) x(n)* h(n) [ (n) 2 (n 1) (n 2)] *[ (n) (n 1) (n 2)] (n) (n 1) (n 2) 2 (n 1) 2 (n 2) (n 3) (n 2) 2 (n 3) (n 4) (n) 3 (n 1) 4 (n 2) 3 (n 3) (n 4)
解 ： (3) (n 4);非 因 果 ， 稳 定 (5) u(3 n); 非 因 果 ， 不 稳 定 (7) 3n u ( n);非 因 果 ， 稳 定 (9) 0.5n u (n); 因 果 ， 稳 定
7 30对 应 于 线 性 时 不 变 系 统 ： (1)已 知 激 励 为 单 位 阶 跃 信 号 之 零 状 态 响 应 （ 阶 跃 响 应 ） 是 g (n),试 求 冲 击 响 应 h(n); ( 2 )已 知 冲 激 响 应 h ( n )， 试 求 阶 跃 响 应 g ( n )。
1 3
y (1)
1
4 9
30
31 32
32
........
y(n)
30
31
32 3n
3n
3 3n 2
u (n )
7－12 解 差 分 方 程 。 (1) y ( n ) 3 y ( n 1) 2 y ( n 2 ) 0 , y ( 1) 2 , y ( 2 ) 1 (2)y (n) 2 y (n 1) y (n 2) 0, y(0) y(1) 1
解 ： （1） 特 征 方 程 2＋ 3 ＋ 2＝ 0 1 1, 2 2
齐 次 解 ： y (n ) C1(1)n C 2 (2)n
由 y (1)
2, y(2) 1
C
1
C
1
1 4
1C 2 C2
2
1
2
C C
1 2
4
1
2
y (n) 4(1)n 12(2)n
解：（2）特征方程2＋2＋1＝01 2 1
第七章习题讲解
7－ 2分 别 给 出 以 下 各 序 列 的 图 形 。 (1) x ( n ) n u ( n ) (2)x(n) 2nu(n)
(3)x(n) ( 1 )n u(n) 2 (1)
(2)
(3)
7 4判 断 以 下 各 序 列 是 否 周 期 性 的 ， 如 果 是 周 期 性 的 ，