最新小升初数学衔接班第7讲——重新认识图形
小升初数学衔接班教程

例 4:计算: 1 2 2 3 3 4 4 5 3 1 5 2 7 3 9 4
3 4 5 6 3 4 5 6
模仿练习
计算:(1 5 3 5 9 5 )(1 1 3 1 9 1 ) 99 33 11 99 33 11
加法交换律:a b b a ;
加法结合律:(a b) c a (b c) ;
乘法交换律: a b b a
乘法结合律: a b c a (b c)
乘法分配律: a (b c) a b a c 减法的性质: a b c a (b c)
思路点拨 以上的每个分数的分母正好是相邻两个自然数的积,而且分子正好是分母
两个因数的差(1),我们可以直接利用裂项公式进行裂项产生加减抵消后化繁
为简。
模仿练习
1 1 4
4
1
7
1 7 10
00
例 2:计算:975×0.25+ 9 3 76 -9.75
4
模仿练习
糖果工作室原创文档
数学
小升初衔接班教程
目录
糖果工作室原创文档
第一讲 第二讲 第三讲 第四讲 第五讲 第六讲 第七讲 第八讲 第九讲 第十讲 第十一讲 第十二讲 第十三讲 第十四讲 第十五讲
计算中的技巧 1 ·········································································· 行程问题 5 ················································································· 工程问题 8 ················································································· 图形的面积 17 ············································································· 有理数 21 ····················································································· 有理数的加减法 24 ······································································ 有理数的乘除法 28 ······································································ 有理数的乘方 科学计数法 30 ·················································· 整式 33 ·························································································· 一元一次方程 35 ··········································································· 实际问题与一元一次方程 39 ························································· 图形的初步认识 43 ········································································ 角 45 ······························································································ 相交线 平行线 51 ········································································· 平行线的性质 命题 定理 54 ·························································
幼小衔接认识图形数学教案范文通用

幼小衔接认识图形数学教案范文通用教案名称:幼小衔接认识图形数学教案一、教学内容1. 学习平面图形的基本特征,如正方形、长方形、圆形和三角形。
2. 学会用语言描述图形的形状和特征。
3. 培养学生的观察、操作和交流能力。
二、教学目标1. 学生能够认识并说出常见平面图形的名称,了解它们的基本特征。
2. 学生能够通过观察、操作和交流,进一步体会数学与生活的密切联系。
3. 培养学生的观察能力、操作能力和语言表达能力,提高学生的空间观念。
三、教学难点与重点重点:认识四种常见的平面图形,理解它们的特点。
难点:用语言描述图形的形状和特征。
四、教具与学具准备教具:多媒体课件、黑板、粉笔、图形卡片。
学具:学生用书、练习本、彩笔、剪刀、胶水。
五、教学过程1. 实践情景引入(5分钟)教师通过展示课件,呈现一个生活中的场景,如公园、学校等,让学生观察并找出其中的平面图形。
引导学生发现数学与生活的联系。
2. 图形认知(10分钟)教师出示各种平面图形卡片,如正方形、长方形、圆形和三角形,引导学生认识这些图形,并用语言描述它们的形状和特征。
3. 操作活动(10分钟)学生分组进行操作活动,用剪刀剪出各种平面图形,并拼贴成一个新的图形。
培养学生动手操作能力和创新意识。
4. 课堂练习(10分钟)学生独立完成练习题,如判断题、连线题等,巩固所学知识。
教师巡回指导,及时解答学生疑问。
六、板书设计板书内容:认识四种常见的平面图形(正方形、长方形、圆形、三角形),以及它们的特征。
七、作业设计作业题目:1. 判断题:(1)正方形的四条边都相等。
()(2)长方形的对边平行且相等。
()(3)圆形的四条边都相等。
()(4)三角形的三个角都相等。
()2. 连线题:将下列图形与它们的名称连线:正方形______ 长方形______ 圆形______ 三角形______答案:1. (1)√(2)√(3)×(4)×2. 正方形——>______ 长方形——>______ 圆形——>______ 三角形——>______八、课后反思及拓展延伸课后反思:在本节课中,学生掌握了四种常见平面图形的特征,并能用语言描述它们的形状。
衔接点04 几何图形(解析版)-2024小升初数学暑假衔接讲义

衔接点04几何图形小学阶段主要学习了常见的平面几何图形(三角形、四边形、圆)的周长与面积、立体图形(长、正方体、圆柱、圆锥)的表面积与体积。
培养的核心数学素养是学生的几何直观、空间观念和运算能力。
初中阶段较小学阶段在几何图形方面变化极大:不再是停留在建立图形的直观表象和对图形特征的研究上,而要转入对其性质较为系统的研究。
中学数学还要求进行数学证明,这对从来没有进行过数学证明的学生来说,要掌握从论据推出结论的方法,来表明论据与结论之间必然的逻辑联系是有一定难度的。
培养的核心数学素养是学生的几何直观、抽象能力、推理能力等。
在初中几何中,随着变量和演绎推理证明等知识的进入,初中学生学习几何就需要提高相应的思维能力,比如抽象思维,推理能力等等。
难度提升,思维的层次也大为不同。
如“三角形的内角和等于180°”这个定理,小学教材中是由实验得出的。
初中要强调说明不能满足于实验,而必须从理论上给予严格论证。
题型探究题型1、割补法求面积(一)平移与对称 (3)题型2、割补法求面积(二)旋转 (8)题型3、和差法求面积 (11)题型4、整体代换法 (16)题型5、等积变换法求面积(体积) (18)题型6、差不变思想(原理) (22)题型7、容斥原理(韦恩图) (24)题型8、平面图形的拼切重组问题(含翻折) (27)题型9、立体图形的拼切重组问题 (31)培优精练A组(能力提升) (37)B组(培优拓展) (45)1、基本公式正方形:4C a =;S a a =⨯。
长方形:()2C a b =+⨯;S ab =。
平行四边形:S ah =。
三角形:2S ah =÷。
梯形:()2S a b h =+⨯÷。
圆:2C d r ππ==;2S r π=。
正方体S 表=6a a ⨯⨯;V a a a=⨯⨯长方体S 表()2ab ah bh =++⨯;V abh=圆柱体、圆锥体(h :高;S :底面积;r :底面半径)圆柱侧面积:2S r h π=⋅;圆柱表面积:222S r h r ππ=⋅+;圆柱体积:V S h =⋅;圆锥体积:13V S h =⋅2、求几何图形面积常见方法及运用:差不变思想(原理):即利用等式的性质来求面积,若S 甲=S 乙,则S 甲+S 空白=S 乙+S 空白,S 甲-S 空白=S 乙-S 空白。
小升初衔接培训资料(学生版)

小升初衔接培训1内容提要:1.如果整数A 除以整数B(B ≠0)所得的商A/B 是整数,那么叫做A 被B 整除. 0能被所有非零的整数整除2..能被7整除。
能被11整除的数的特征: ①抹去个位数 ②减去原个位数 ③其差能被11整除 例题例1已知两个三位数328和92x 的和仍是三位数75y 且能被9整除。
求x,y例2已知五位数x 1234能被12整除,求x例3求能被11整除且各位字都不相同的最小五位数练习:1 分解质因数:(写成质因数为底的幂的連乘积)①593 ② 1859 ③1287 ④3276 ⑤10101 ⑥102962 若四位数a 987能被3整除,那么 a=_______________3 若五位数3412X 能被11整除,那么 X =__________4 当 m=_________时,535m 能被25整除9610能被7整除5当n=__________时,n6能被11整除的最小五位数是________,最大五位数是_________78能被4整除的最大四位数是____________,能被8整除的最小四位数是_________98个数:①125,②756,③1011,④2457,⑤7855,⑥8104,⑦9152,⑧70972中,能被下列各数整除的有(填上编号):6________,8__________,9_________,11__________10从1到100这100个自然数中,能同时被2和3整除的共_____个,能被3整除但不是5的倍数的共______个。
11由1,2,3,4,5这五个自然数,任意调换位置而组成的五位数中,不能被3整除的数共有几个?为什么?1234能被15整除,试求A的值。
12己知五位数A13求能被9整除且各位数字都不相同的最小五位数。
14求在十进制中,各位数码都是0或1,并能被225整除的最小正整数(1989年全国初中联赛)小升初衔接培训2内容提要1 质数的定义:如果一个大于1的正整数,只能被 整除,那么这个正整数叫做质数(质数也称素数)。
新初一数学通用版小升初数学衔接班

新初一数学通用版小升初数学衔接班第1讲——学法指导课后练习(答题时间:45分钟)1、探究数字“黑洞”:“黑洞”原指一种非常奇怪的天体,它体积小,密度大,吸引力强,任何物体到了它那里都别想再“爬”出来,无独有偶,数字中也有类似的“黑洞”,满足某种条件的所有数字,通过一种运算,都能被它吸进去,无一能逃脱它的“魔掌”,譬如:任意找一个为3的倍数的数,先把这个数的每一个数位上的数字都立方,再相加,得到一个新数,然后把这个新数的每一个数位上的数字再立方、求和……,重复运算下去,就能得到一个固定的数T _________,我们称之为数字“黑洞”。
2、A、B、C、D、E、F六个足球队进行单循环比赛,当比赛到某一天时,统计出A、B、C、D、E五队已分别比赛了5、4、3、2、1场球,则还没有与 B队比赛的球队是()A. C队B. D队C. E队D. F队3、用大小相同的正六边形瓷砖按如图所示的方式来铺设广场,中间的正六边形瓷砖记为A,定义为第一组;在它的周围铺上6块同样大小的正六边形瓷砖,定义为第二组;在第二组的外围用同样大小的正六边形瓷砖来铺满,定义为第三组……按这种方式铺下去,用现有的2005块瓷砖最多能完整地铺满多少组还剩几块瓷砖4、用“<”、“>”定义新运算:对于任意数,a b,都有a b a>=。
<=和a b b例如,323><>=_________。
<=,322>=,则(20062005)(20042003)5、如图,是用火柴棍摆出的一系列三角形图案,按这种方式摆下去,当每边上摆20(20n=)根火柴棍时,需要的火柴棍总数为______根。
6、一根绳子弯曲成如图1所示的形状。
当用剪刀像图2那样沿虚线a把绳子剪断时,绳子被剪为5段;当用剪刀像图3那样沿虚线b(b,a b(2)n-a n41n+n+ B. 42C. 43n+n+ D. 457、如果有2003名学生排成一列,按1,2,3,4,3,2,1,2,3,4,3,2,1…的规律报数,那么第2003名学生所报的数是()A. 1B. 2C. 3D. 48、如图,有两张形状、大小完全相同的直角三角形纸片(同一个直角三角形的两条直角边不相等),把这两个三角形的相等的边靠在一起(两张纸片不重叠),可以拼出若干种图形,其中,形状不同的四边形有()A. 3种B. 4种C. 5种D. 6种9、一只箱子里装有蟋蟀和蜘蛛,共46只脚(每只蟋蟀6只脚,每只蜘蛛8只脚),已知蜘蛛比蟋蟀多,那么蜘蛛有________只。
小升初数学衔接班第7讲
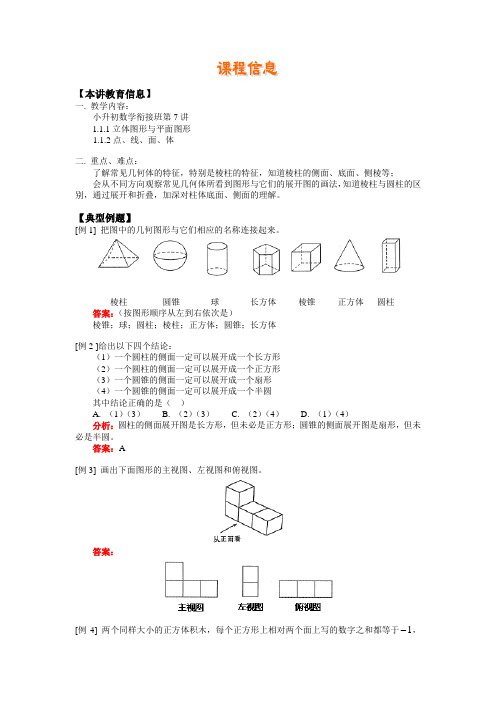
【本讲教育信息】一. 教学内容:小升初数学衔接班第7讲1.1.1立体图形与平面图形1.1.2点、线、面、体二. 重点、难点:了解常见几何体的特征,特别是棱柱的特征,知道棱柱的侧面、底面、侧棱等;会从不同方向观察常见几何体所看到图形与它们的展开图的画法,知道棱柱与圆柱的区别,通过展开和折叠,加深对柱体底面、侧面的理解。
【典型例题】[例1] 把图中的几何图形与它们相应的名称连接起来。
棱柱圆锥球长方体棱锥正方体圆柱答案:(按图形顺序从左到右依次是)棱锥;球;圆柱;棱柱;正方体;圆锥;长方体[例2 ]给出以下四个结论:(1)一个圆柱的侧面一定可以展开成一个长方形(2)一个圆柱的侧面一定可以展开成一个正方形(3)一个圆锥的侧面一定可以展开成一个扇形(4)一个圆锥的侧面一定可以展开成一个半圆其中结论正确的是()A. (1)(3)B. (2)(3)C. (2)(4)D. (1)(4)分析:圆柱的侧面展开图是长方形,但未必是正方形;圆锥的侧面展开图是扇形,但未必是半圆。
答案:A[例3] 画出下面图形的主视图、左视图和俯视图。
答案:,[例4] 两个同样大小的正方体积木,每个正方形上相对两个面上写的数字之和都等于1现将两个正方体并列放置,看得见的五个面上的数如图所示,则看不见的七个面上的数字之和为( )A. 20-B. 21-C. 19-D. 18-分析:用整体思想去考虑,两个正方体共12个面,6对。
所以,所有面的和是6个1-,设其他七个面的数字之和为x ,则6154321⨯-=+++++x ,所以21-=x 。
答案:B[例5] 将直角三角形绕一条边所在直线旋转一周后形成的几何体不可能是( )。
答案:C[例6] 画出下面立体图形的主视图、左视图和俯视图答案:[例7] 一个五棱柱如图所示,它的底面边长都是4厘米,侧棱长6厘米,则(1)这个五棱柱共有________个面;这个五棱柱共有_______条棱,它们的长分别为__________。
2024年幼小衔接认识图形数学教案范文通用
2024年幼小衔接认识图形数学教案范文通用一、教学内容本节课选自《幼小衔接数学》教材第四章第三节,详细内容为认识图形。
通过本章学习,学生将掌握平面图形如圆形、正方形、长方形、三角形和星形的基本特征,并学会区分不同图形。
二、教学目标1. 让学生掌握基本的平面图形,如圆形、正方形、长方形、三角形和星形;2. 培养学生观察、分析和解决问题的能力,使学生能够运用所学知识解决生活中的实际问题;3. 培养学生的空间观念,激发学生对数学学习的兴趣。
三、教学难点与重点教学难点:图形的区分和识别。
教学重点:掌握各种图形的基本特征,并能应用于实际情景。
四、教具与学具准备1. 教具:各种图形卡片、磁性黑板、挂图、多媒体设备;2. 学具:学生用图形卡片、练习册、彩笔。
五、教学过程1. 导入:通过展示生活中常见的图形,引导学生观察、讨论,激发学生对图形的兴趣。
2. 新课导入:教师展示教材中的各种图形,引导学生认识并说出它们的名字,讲解各种图形的基本特征。
并与其他同学分享。
4. 例题讲解:讲解图形识别和区分的方法,引导学生通过观察、比较、分析来解决问题。
5. 随堂练习:学生完成练习册上的图形题目,巩固所学知识。
六、板书设计1. 图形名称:圆形、正方形、长方形、三角形、星形;2. 图形特征:用简洁明了的语言描述各种图形的基本特征;3. 举例说明:生活中的图形实例。
七、作业设计1. 作业题目:请找出生活中的5个图形,并描述它们的特点。
2. 答案:例如:①圆形的硬币,特点是边界为曲线,面积相等;②正方形的瓷砖,特点是四条边相等,四个角为直角;③长方形的书本,特点是两对边平行且相等;④三角形的衣架,特点是三条边,三个角;⑤星形的贴纸,特点是有多个角和边。
八、课后反思及拓展延伸1. 反思:本节课学生对图形的认识基本达到预期目标,但在区分图形时仍有一定难度,需要在今后的教学中加强练习。
2. 拓展延伸:引导学生观察生活中的其他图形,如椭圆形、梯形等,并了解它们的特点。
2024年幼小衔接认识图形数学教案范文通用
2024年幼小衔接认识图形数学教案范文通用一、教学内容本节课选自幼小衔接数学教材第三章《认识图形》,详细内容包括平面图形如圆形、正方形、三角形的识别和分类,以及简单的图形组合和分解。
二、教学目标1. 让学生能够识别并命名圆形、正方形、三角形等基本平面图形。
2. 培养学生通过观察、比较、分类等方法,提高空间想象力和逻辑思维能力。
3. 培养学生运用图形进行创意表达和解决简单问题的能力。
三、教学难点与重点教学难点:图形的组合和分解,以及不同图形的特征识别。
教学重点:圆形、正方形、三角形的识别和分类。
四、教具与学具准备1. 教具:图形卡片、磁性黑板、挂图、多媒体设备。
2. 学具:学生用图形卡片、画纸、彩笔。
五、教学过程1. 实践情景引入利用多媒体展示生活中常见的图形,引导学生观察并说出它们的名字。
2. 例题讲解(1)展示圆形、正方形、三角形的图形卡片,引导学生观察并说出它们的特征。
(2)通过举例,讲解图形的组合和分解。
3. 随堂练习(1)让学生用图形卡片进行分类,将相同的图形放在一起。
(2)邀请学生上台展示,分享自己的分类方法。
4. 小组讨论(1)圆形、正方形、三角形有什么共同点和不同点?(2)如何用这些图形组合成一个新的图形?6. 课堂小结通过提问方式检查学生对本节课内容的掌握情况。
六、板书设计1. 《认识图形》2. 内容:(1)圆形、正方形、三角形的特点(2)图形的分类方法(3)图形的组合和分解七、作业设计1. 作业题目:(1)请用圆形、正方形、三角形组合成一个新的图形,并画在纸上。
(2)列举生活中常见的图形,并说出它们的名字。
2. 答案:(1)略(2)如:车轮(圆形)、窗户(正方形)、三角形屋顶等。
八、课后反思及拓展延伸1. 课后反思:教师应关注学生对图形的认识和分类掌握情况,针对学生存在的问题进行有针对性的辅导。
2. 拓展延伸:(1)引导学生观察生活中的图形,提高对图形的认识。
(2)鼓励学生用图形创作有趣的画作,激发创造力。
【精品小升初数学】图形的认识 +答案
图形的认识知识集结知识元图形的认识知识讲解•一、平面图形的分类及识别1.概念:有些几何图形(如线段、角、三角形、长方形、圆等)的各个部分都在同一平面内,它们是平面图形.2.平面图形分类:(1)三角形:按边分有等腰三角形,不等腰三角形.按角分有:锐角三角形.直角三角形,钝角三角形.(2)四边形:任意四边形,平行四边形,梯形.(3)圆形:扇形.二、角的概念及分类1.角的基本概念:从静态角度认识角:由一个点出发的两条射线组成的图形叫角;从动态角度认识角:一条射线绕着它的顶点旋转到另一个位置,则这两条射线组成的图象叫角.有公共端点的两条射线组成的图形叫做角,这个公共端点叫做角的顶点,这两条射线叫做角的边.(1)因为射线是向一方无限延伸的,所以角的两边无所谓长短,即角的大小与它的边长无关.(2)角的大小可以度量,可以比较.(3)根据角的度数,角可以分为锐角、直角、钝角、平角、周角.角的表示:角可以用大写英文字母、阿拉伯数字或小写的希腊字母表示,如∠1,∠α,∠BAD 等.2.角的分类:根据角的度数,角可以分为锐角、直角、钝角、平角、周角.平角:180°的角,当角的两边在一条直线上时,组成的角叫做平角.即射线OA绕点O旋转,当终边在始边OA的反向延长线上时所成的角;直角:90°的角,即线OA绕点O旋转,当终边与始边垂直时所成的角,平角的一半叫做直角;锐角:大于0°小于90°的角,小于直角的角叫做锐角;钝角:大于90°小于180°的角,大于直角且小于平角的角叫做钝角.周角:360°的角,即射线OA绕点O旋转,当终边与始边重合时所成的角.三、直线、线段和射线的认识1.概念:直线:一根拉得很紧的线,就给我们以直线的形象,直线是直的,并且是向两方无限延伸的.一条直线可以用一个小写字母表示.线段:直线上两个点和它们之间的部分叫做线段,这两个点叫做线段的端点.一条线段可用它的端点的两个大写字母来表示.射线:直线上一点和它一旁的部分叫做射线.这个点叫做射线的端点.一条射线可以用端点和射线上另一点来表示.注意:(1)线和射线无长度,线段有长度.(2)直线无端点,射线有一个端点,线段有两个端点.2.直线、射线、线段区别:直线没有端点,两边可无限延长;射线有一端有端点,另一端可无限延长;线段,有两个端点,而两个端点间的距离就是这条线段的长度.四、垂直与平行的特征及性质1.垂线的定义:两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直.其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.直线AB,CD互相垂直,记作“AB⊥CD”(或“CD⊥AB”),读作“AB垂直于CD”(或“CD 垂直于AB”).2.垂线的性质:性质1:过一点有且只有一条直线与已知直线垂直.性质2:连结直线外一点与直线上各点的所有线段中,垂线段最短.简称:垂线段最短.3.垂直的判定:垂线的定义.4.平行线的概念:在同一个平面内,不相交的两条直线叫做平行线.平行用符号“∥,如“AB∥CD”,读作“AB 平行于CD”.5.平行线的判定方法:(1)平行于同一条直线的两直线平行.(2)垂直于同一条直线的两直线平行.(3)平行线的定义.五、平行四边形的特征及性质平行四边形的概念:1.两组对边分别平行的四边形叫做平行四边形.平行四边形用符号“□ABCD”,如平行四边形ABCD记作“□ABCD”.(1)平行四边形属于平面图形.(2)平行四边形属于四边形.(3)平行四边形中还包括特殊的平行四边形:矩形,正方形和菱形等.(4)平行四边形属于中心对称图形.2.平行四边形的性质:主要性质(矩形、菱形、正方形都是特殊的平行四边形.)(1)如果一个四边形是平行四边形,那么这个四边形的两组对边分别相等.(简述为“平行四边形的两组对边分别相等”)(2)如果一个四边形是平行四边形,那么这个四边形的两组对角分别相等.(简述为“平行四边形的两组对角分别相等”)(3)夹在两条平行线间的平行线段相等.(4)平行四边形的面积等于底和高的积.(可视为矩形)(5)过平行四边形对角线交点的直线,将平行四边形分成全等的两部分图形.(6)平行四边形是中心对称图形,对称中心是两对角线的交点.(7)平行四边形不是轴对称图形,矩形和菱形是轴对称图形.注:正方形,矩形以及菱形也是一种特殊的平行四边形,三者具有平行四边形的性质.六、长方形的特征及性质长方形:是一种平面图形,长方形的四个角都是直角,同时长方形的对角线相等.长方形的性质:1.长方形的4个内角都是直角;2.长方形对边相等;3.长方形既是轴对称图形,也是中心对称图形(对称轴是任何一组对边中点的连线),它至少有两条对称轴.对称中心是对角线的交点.4.长方形是特殊的平行四边形,长方形具有平行四边形的所有性质七、正方形的特征及性质1.概念:有一组邻边相等且一个角是直角的平行四边形叫做正方形.2.性质:(1)边:两组对边分别平行;四条边都相等;相邻边互相垂直(2)内角:四个角都是90°;(3)对角线:对角线互相垂直;对角线相等且互相平分;每条对角线平分一组对角;(4)对称性:既是中心对称图形,又是轴对称图形(有四条对称轴).(5)正方形具有平行四边形、菱形、矩形的一切性质.(6)特殊性质:正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的夹角是45°;正方形的两条对角线把正方形分成四个全等的等腰直角三角形.(7)正方形是特殊的长方形.八、梯形的特征及分类1.概念:梯形是指一组对边平行而另一组对边不平行的四边形.2.分类:(1)直角梯形:有一个角为直角的梯形为直角梯形(2)等腰梯形:两腰相等的梯形叫做等腰梯形(3)一般梯形.九、三角形的特征及分类1.三角形具有稳定性.三内角之和等于180度,根据角可以分为锐角三角形(每个角小于90°),直角三角形(有一个角等于90°),钝角三角形(有一个角大于90°).任意两边之和大于第三边,任意两边之差小于第三边.2.三角形的分类①按角分判定法一:锐角三角形:三个角都小于90°.直角三角形:可记作Rt△.其中一个角必须等于90°.钝角三角形:有一个角大于90°.判定法二:锐角三角形:最大角小于90°.直角三角形:最大角等于90°.钝角三角形:最大角大于90°.其中锐角三角形和钝角三角形统称为斜三角形.②按边分不等边三角形;等腰三角形;等边三角形.十、立体图形的分类及识别1.立体几何图形:从实物中抽象出来的各种图形,统称为几何图形,几何图形是数学研究的主要对象之一.有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各个部分不都在同一平面内,它们是立体图形.由一个或多个面围成的可以存在于现实生活中的三维图形.点动成线,线动成面,面动成体.即由面围成体,看一个体最多看到立体图形实物三个面.2.常见立体几何图形及性质:(1)正方体:有8个顶点,6个面.每个面面积相等(或每个面都有正方形组成).有12条棱,每条棱长的长度都相等.(正方体是特殊的长方体)(2)长方体:有8个顶点,6个面.每个面都由长方形或相对的一组正方形组成.有12条棱,相对的4条棱的棱长相等.(3)圆柱:上下两个面为大小相同的圆形.有一个曲面叫侧面.展开后为长方形或正方形或平行四边形.有无数条高,这些高的长度都相等.(4)圆锥:有1个顶点,1个曲面,一个底面.展开后为扇形.只有1条高.四面体有1个顶点,四面六条棱高.(5)直三棱柱:三条侧棱切平行,上表面和下表面是平行且全等的三角形.(6)球:球是生活中最常见的图形之一,例如篮球、足球都是球,球是由一个面所围成的几何体.例题精讲图形的认识例1.(2019∙长沙模拟)把平角分成两个角,其中一个是钝角,那么另一个肯定是()A.锐角B.直角C.钝角【解析】题干解析:其中钝角是大于90°,小于180°的角,用“180-钝角”所得的角的度数小于90度,所以另一个角是锐角;例2.(2014春∙上海校级期末)下列各图中()不是平行四边形。
小升初数学衔接班教材
目录第一讲计算中的技巧 (1)第二讲行程问题 (5)第三讲工程问题 (8)第四讲图形的面积 (17)第五讲有理数 (21)第六讲有理数的加减法 (24)第七讲有理数的乘除法 (28)第八讲有理数的乘方科学计数法 (30)第九讲整式 (33)第十讲一元一次方程 (35)第十一讲实际问题与一元一次方程 (39)第十二讲图形的初步认识 (43)第十三讲角 (45)第十四讲相交线平行线 (51)第十五讲平行线的性质命题定理 (54)第一讲计算的技巧知识导航我们在进行运算时,除了熟练掌握好运算法则外,还要通过观察和分析,找出题目中数的特点,合理、有效地进行计算。
整数、小数与分数四则混合运算常用的方法、技巧如下:1、运算法则:先乘除后加减;先算小括号,再算中括号;同级运算从左到右依次计算。
2、运算定律与性质:加法交换律:a+;加法结合律:)=ba+b+a+=+;b+()c(cab 乘法交换律:a⨯乘法结合律:)=bba⨯⨯=⨯a⨯⨯(cbacb乘法分配律:ccabb(c--(减法的性质:)=-a+bb⨯)aaa⨯c±=⨯±除法的性质:)÷=÷÷a⨯(cbbca3、灵活运用通分和约分4、分数、小数化成统一的形式再计算,一般是分数化成小数。
5、凑整法:运用运算定律,使式子中一些数凑成整十、整百或整千的数再计算。
我们通常是利用运算律将一些数凑成整一、整十或整百再计算。
6、分组分解法:利用交换律和结合律对式子进行分组求解,最后再综合求解。
7、综合方法:计算比较复杂的式子时要多种方法一起用。
重难点运算法则和运算定律与性质的掌握和应用。
易错点去括号是的变号法则,尤其是括号前是减号。
精典例题例1:21 +61+121+201+301+421+561+721+901 思路点拨 以上的每个分数的分母正好是相邻两个自然数的积,而且分子正好是分母两个因数的差(1),我们可以直接利用裂项公式进行裂项产生加减抵消后化繁为简。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小升初数学衔接班第7讲——重新认识图形一、学习目标:通过学习三角形的边角关系及中线、高线、角平分线等内容,体会初中几何与小学的不同,掌握基本的推理、论证的方法,以便更快适应中学的学习。
二、学习重点:学会基本的推理、论证的方法。
三、课程精讲:1、知识回顾在小学,我们学习过一些几何图形,比如三角形:(1)三角形内角和(量一量、拼一拼,找出规律)(2)三角形三边的关系(摆一摆,找出规律)提问:在测量三角形的内角和时,你真能测量得绝对精确、没有一点误差吗?在把三角形的内角拼接为一个平角时,你真的认为能拼成一个平角吗?会不会只是很接近平角呢?在用小棍摆三角形时,你发现了两边之和必须要大于第三边。
这个结论对所有长度的小棍都成立吗?你没有摆的其他长度也是这样吗?2、新知探秘知识点一为何要推理?例1、图(1)中,线段AB、CD哪一条长?图(2)中,线段AB、AC哪一条长?图(3)中,两个带阴影的椭圆哪一个大?图(4)中,,a b两条直线之间一样宽吗?知识点二推理的依据推理时要做到言必有据,那什么是推理的依据呢?这就是学过的定义、公理和定理。
(1)定义:对于一个名词或术语的意义的说明就叫做定义。
比如,射线的定义为“直线上一点和它一旁的部分叫做射线”、角的定义为“有公共端点的两条射线组成的图形叫做角”等。
(2)公理:被人类长久以来的实践所证实,作为推理依据的事实叫做公理。
比如,“经过两点有且只有一条直线”、“在所有连接两点的线中,线段最短”等。
(3)定理:用逻辑推理的方法判断为正确的命题叫做定理。
以后,我们将会学习到许多定理。
例2、已知,如图,D是AB中点,E是AC中点,且AB=AC。
求证:AD=AE。
思路导航:有同学认为这显然成立,却不能说出推理的依据,这是不可取的。
解答:D是AB中点(已知)∴12AD AB=(线段中点定义)E是AC中点(已知)∴12AE AC=(线段中点定义)又AB=AC(已知)∴1122AB AC=(等式的性质)即AD=AE(等量代换)点津:要养成“讲道理”的习惯,初学时应在每一步之后注明推理的依据。
在小学阶段,“三角形内角和为180°”的证明,需要用到平行线的相关性质;而证明“三角形两边之和大于第三边”要用到公理“在所有连接两点的线中,线段最短”。
例3、如图,已知△ABC中,AB=AC=4,P是BC上任意一点,PD⊥AB于D,PE⊥AC于E,若△ABC的面积为6,求PD+PE的值。
思路导航:仔细体会题目意思,“P 是BC 上任意一点”,明确是要求出P 在BC 上的任何位置时,PD + PE 的值。
再进一步分析,若PD + PE 的值不变的话,只要假设P 在某个特殊的位置,就能比较方便地求出PD +PE 的值了。
但这并不是推理证明。
解答: 连接APPD ⊥AB (已知)∴12ABP S AB PD ∆=⨯(三角形面积公式) PE ⊥AC (已知)∴12ACP S AC PE ∆=⨯(三角形面积公式) ∴1122ABP ACP S S AB PD AC PE ∆∆+=⨯+⨯(等式的性质)即1164422PD PE =⨯⨯+⨯⨯∴3PD PE +=(等式的性质) 点津:这里的线段AP 是我们为了解题方便而作出来的,这叫做辅助线。
通常辅助线用虚线表示。
添加辅助线来解题,是我们以后解几何题时常用的办法。
在中学,对于解答题,并不是只要求出得数即可,而应重视解答过程中的论证及其依据。
知识点三 三角形的外角三角形一条边的延长线与其相邻的一条边组成的角,叫做三角形的外角。
关于三角形的外角有如下定理:定理1:三角形的一个外角等于与它不相邻的两个内角的和。
定理2:三角形的一个外角大于与它不相邻的任意一个内角。
定理3:三角形的外角和为360(每个顶点处的外角只取其中一个)。
在中学学习中,同学们一定不能只注重结论,还必须弄清楚其来源和推理过程。
例4、已知:如图,在ABC ∆中,75A ∠=,BE 是AC 边上的高,CF 是AB 边上的高,H 是BE 和CF 的交点。
求BHC ∠的度数。
思路导航:无论解答题还是证明题,其解答或证明过程都是将已知条件和结论联系起来。
因此,我们的任务就是将“BHC ∠”与“75A ∠=”联系起来,过程中可能会用到条件“BE 是AC 边上的高,CF 是AB 边上的高”。
解答:BE 是AC 边上的高CF 是AB 边上的高(已知)∴90AEB ∠=,90BFC ∠=(高线定义) 在ABE ∆中,180A ABE AEB ∠+∠+∠=(三角形内角和定理)75A ∠=(已知) 90AEB ∠=(已证)∴180759015ABE ∠=--=(等式的性质) 即15FBH ∠= 在BHF ∆中,BHC FBH BFH ∠=∠+∠(三角形的一个外角等于与它不相邻的两个内角的和)90BFH ∠=(已证) 15FBH ∠=(已证)∴1590105BHC ∠=+=点津:有的同学认为只有证明题才需要推理依据,计算题与证明题不同,只要算出得数即可。
这个观念是极其错误的,计算题在计算过程中也存在着推理论证,也要求言之有据!知识点四 三角形的角平分线在三角形中,一个角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段,叫做这个三角形的角平分线。
例5、已知:如图,ABC ∆中,AD 是角平分线,40B ∠=,50C ∠=。
求ADC ∠的度数。
思路导航:由于已知50C ∠=,所以,为求ADC ∠的度数,只需再知道DAC ∠的度数就可以了。
为求DAC ∠,只需再知道BAC ∠的度数就可以了。
为求BAC ∠,只需知道B ∠和C ∠的度数就可以了。
而B ∠和C ∠的度数已知,所以,问题得解。
解答:在ABC ∆中,180BAC B C ∠+∠+∠=(三角形内角和定理)∴180BAC B C ∠=-∠-∠(等量减等量,差相等。
可简称为等式的性质) 又40B ∠=,50C ∠=(已知)∴180405090BAC ∠=--=(等量代换) 又AD 平分BAC ∠(已知)∴12DAC BAC ∠=∠(角平分线定义)∴190452DAC ∠=⨯=(等量代换)在ADC ∆中,180DAC ADC C ∠+∠+∠=(三角形内角和定理) ∴180ADC DAC C ∠=-∠-∠(等式的性质) 180455085=--=(等量代换)点津:我们在分析题目的过程中,经常使用“要求什么,只要求什么”的思维方法,这种思维方法即为分析法,是一种很常用的方法,在分析解题思路时很有用。
我们在分析、听讲、阅读几何问题时,一定要结合几何图形来进行。
四、知识提炼导图:五、目标期望:通过本讲的学习,希望同学们了解初中研究几何的方法与小学不同,主动、自觉地培养自己理性思维的习惯,即演算、论证过程要言之有据。
希望同学们在后续的学习过程中,形成这样的观点:学习几何的过程中最重要的不是许许多多的结论,而是如何得出这些结论的过程!本讲选用三角形为例来说明以上观点,希望同学们能用新的观点重新研究小学的一些结论(比如三角形的内角和、三边的大小关系等),多思考为什么能得出这些结论。
六、下讲预告:著名数学教育家波利亚如是说:“要想成为一个好的数学家,你必须首先是一个好的猜想家,数学家的创造性工作成果是论证推理,即证明,但这个证明是由合情推理、由猜想来发现的。
”国家义务教育课程标准中明确指出“培养学生创新意识”、“学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程。
”下一讲,我们将学习如何观察、实验、猜测,它们是创造的基石。
【同步练习】(答题时间:45分钟) 1、火眼金睛:(1)下列说法中正确说法的个数是( ) ①钝角三角形有两条高在三角形内部;②三角形三条高至多有两条不在三角形内部;③三角形三条高的交点不是在三角形内部,就是在三角形外部; ④钝角三角形三个内角的平分线的交点一定不在三角形内部。
A. 1个 B. 2个 C. 3个 D. 4个(2)如果三角形三边长分别为1-a 、a 、1+a ,则a 的取值范围是( ) A. 0>a B. 10<<a C. 2>a D. 21<<a(3)一个等腰三角形的周长是11,其中一边长是3,则其他两边长是( ) A. 3和5 B. 4和4 C. 3和5或4和4 D. 不能确定(4)五条线段的长分别为1,2,3,4,5,以其中三条线段为边长可以构成的三角形的个数为( )A. 3个B. 4个C. 5个D. 6个 (5)如图,4,3,2,1∠∠∠∠满足下列( )关系式A. 3421∠-∠=∠+∠B. 4321∠+∠=∠+∠C. 3421∠-∠=∠-∠D. 4321∠-∠=∠-∠2、对号入座:(1)已知:如图,ABC ∆中,OA 、OB 分别平分BAC ∠、ABC ∠,若 100=∠AOB ,则=∠C ;(2)已知:如图,AD 、AE 分别是ABC ∆的高和角平分线,若 33=∠B , 67=∠C ,则=∠1 ,=∠2 ,=∠3 ;(3)已知ABC ∆中,BC AD ⊥,AC BE ⊥,垂足为D 、E ,AD =6,BC =10,BE =8。
则AC 的长为_______________;(4)已知ABC ∆中, 36B =∠, 110ACB =∠,AD 平分A ∠,AE 是BC 边上的高,则=∠DAE _______;(5)已知:如图, 40=∠A ,BE 、CE 是ABC ∠、ACB ∠的平分线,BF 、CF 是CBM ∠、NCB ∠的平分线,则=∠E ,=∠F 。
3、牛刀小试:(1)已知:如图,ABC Rt ∆中, 90=∠ACB ,AB CD ⊥,AE 平分CAB ∠。
求证:CFE CEF ∠=∠。
(2)已知:ABC ∆中,D 为AB 边上一点,且AD =AC ,求证:AC AB CD BC -<-。
【试题答案】 1、火眼金睛:(1)A 解析:①钝角三角形只有一条高在三角形内部,错;②三角形三条高不能都不在内部,对;③三角形三条高的交点可以在定点处,错;④钝角三角形三个内角的平分线的交点一定在三角形内部,错。
(2)C 解析:因为,边1a +最长,所以只要满足11a a a -+>+即可,解得2a >。
(3)C 解析:若3为腰长,则底边为11325-⨯=;若3为底边长,则腰长为(113)24-÷=;均能构成三角形。
(4)A 解析:较短边为1和2时,均不能构成三角形; 较短边为1和3时,均不能构成三角形; 较短边为1和4时,均不能构成三角形;较短边为2和3时,能构成三角形的只有2、3、4; 较短边为2和4时,能构成三角形的只有2、4、5; 较短边为3和4时,能构成三角形的只有3、4、5。
