固体中的声波方程
15波动(横波、纵波、行波、简谐波、波长、波速、波动方程)

t
x 20
m
得: u=20m/s
由 = uT = u/ ν = 20/200 = 0.1m
速度和加速度的公式如下:
v y A sin(t 2x / )
18
t
代入相应的量
v 2103 400 sin(400t 20x)
加速度为:
a v 2103 (400 )2 cos(400t 20x)
t x = 1m代入得
v 0.8 sin 400t(m / s) a 320 2 cos(400t)(m / s2 )
19
例2、对于柔软的绳索和弦线中横波波速为 u
F
F为绳索或弦线中张力; 为质量线密度
y(0,0)=0 v0>0 初位相为 φ= -π/2
X
0.2m 0.4m
y Acos(2 t 2x ) T 2
4102 cos(100t 5x
2)m
20
因为:v
y
y( x,
x) u
0
]
所以 v y y(x,t) 12.6cos(100t 5x)(m / s)
第六章
波动
1
6-1、波动学基础
波动是自然界最常见的一种运动形式。例如 机械波:水波、声波、地震波。其传播需要有介质。
电磁波:无线电波、光波、各种射线等,其传播无需 介质。
物质波:近代物理发现实物粒子也具有波性,即物质 波。
各种波性质不同,但又有共性。可以传递能量,可以 产生反射、折射、干涉、衍射等现象。以有限的速率 传播。
初位相不为0时:
y(x,t) Acos[(t x) ]
声波的传播原理

声波的传播原理声波是一种机械波,是由弹性介质中的分子或粒子的振动引起的。
振动的分子或粒子以媒介粒子的形式传递能量,并在媒介中传播。
声波的传播原理可以概括为以下几个方面:1. 振动源:声波的传播离不开振动源。
振动源可以是任何能够产生机械振动的物体,比如声源、声场或其他震动体。
当振动源发生振动时,会使周围的介质粒子产生周期性的压缩和稀疏,从而产生声波。
2. 媒介:声波传播需要介质的存在。
媒介可以是气体、液体、固体或等离子体。
不同的媒介对声波的传播速度和特性有着不同的影响。
3. 粒子的振动:当振动源振动时,它会传递机械能量给媒介中的粒子。
振动源的振动使得粒子沿着振动方向上下振动,并将这种振动从一个粒子传递给相邻的粒子。
4. 粒子之间的相互作用:媒介中的粒子通过弹性力相互作用,将机械能量传递给相邻的粒子。
当一个粒子向外挤压时,周围的粒子被弹性力推向其他方向,从而形成新的压缩和稀疏区域。
这种粒子之间的相互作用使振动在媒介中传播,产生声波。
5. 波动方程:声波的传播可以用声波方程来描述。
声波方程是一个偏微分方程,描述了声波在媒介中的传播规律。
根据介质性质和边界条件的不同,声波方程的具体形式也会有所不同。
6. 传播速度:声波在媒介中传播的速度取决于媒介的性质。
在同一媒介中,声波的传播速度与媒介的性质有关,例如密度、弹性模量和粘性等。
一般来说,固体中的声速最大,液体中次之,气体中最小。
总结起来,声波的传播原理是振动源将机械振动能量传递给媒介中的粒子,通过粒子之间的相互作用和弹性力的作用,从而形成周期性的压缩和稀疏,使声波在媒介中传播。
声波具有一些特性,如频率、振幅和波长等。
频率是指单位时间内声波振动的次数,单位是赫兹(Hz);振幅是指声波的最大振动位移;波长是声波在单位时间内传播的距离。
这些特性与声波的传播速度、介质的性质以及振动源的特性密切相关。
声波在日常生活中有着广泛的应用,比如声波在水中传播可以帮助水生动物进行通信和导航,声波在超声医学中被用于检测和诊断疾病,声波还可以在工业中用于测量、传输信息和检测材料缺陷等。
波义耳定律推导

波义耳定律推导一、引言波义耳定律是描述声波传播的基本定律之一,它指出声波在不同介质中传播时,其传播速度与介质密度和弹性模量有关。
波义耳定律是由法国物理学家波义耳于19世纪初提出的,它在声学研究中具有重要的应用价值。
二、波义耳定律的表述波义耳定律可以用数学公式来表示:v = √(B/ρ)其中,v表示声速,B表示介质的弹性模量,ρ表示介质的密度。
三、推导过程1. 声波的基本概念首先需要了解声波的基本概念。
声波是由物体振动产生的机械波,在空气等介质中以压缩和稀疏的形式传播。
声波具有频率、振幅和相位等特性。
2. 声速定义接下来需要定义声速。
声速是指在某种介质中传播时,单位时间内通过单位长度所需时间。
通常用符号v表示。
3. 声压与密度之间的关系为了推导出波义耳定律公式,还需要了解声压与密度之间的关系。
声压是指声波在介质中引起的压力变化,通常用符号p表示。
密度是指单位体积内物质的质量,通常用符号ρ表示。
根据理想气体状态方程,可以得到声速与介质密度之间的关系:v = √(γP/ρ)其中,γ表示绝热指数,P表示气体压强。
4. 弹性模量接下来需要了解弹性模量。
弹性模量是描述物质抵抗形变能力的物理量,通常用符号E表示。
它越大,则说明物质越难形变。
5. 波义耳定律的推导根据前面所述的知识,可以将声速与介质密度之间的关系改写为:v = √(γE/ρ)将式子中的γE替换为B(即介质的弹性模量),则可以得到波义耳定律公式:v = √(B/ρ)四、应用范围波义耳定律适用于各种不同类型的介质中,包括固体、液体和气体等。
在空气中传播时,声速约为340米/秒;在水中传播时,声速约为1500米/秒;在钢铁中传播时,声速约为5000米/秒。
五、结论波义耳定律是描述声波在不同介质中传播速度的基本定律之一。
它的推导过程基于声波的基本概念、声压与密度之间的关系、弹性模量等知识。
波义耳定律适用于各种不同类型的介质中,并具有重要的应用价值。
波源的振动方程范文

波源的振动方程范文波源是指能够产生波动的物体或者现象。
波源的振动方程是描述波源振动状态的数学公式。
波源振动方程的形式可以根据具体情况而有所不同,下面将介绍几种常见的波源振动方程。
1.机械波的振动方程机械波是由物质粒子的振动传递而产生的波动,可以通过波源的振动方程来描述。
机械波的振动方程一般为:y(x, t) = A * sin(kx - ωt + φ)其中,y(x,t)表示波在x位置、t时间的位移,A是振幅,k是波数,ω是角频率,φ是相位差。
2.声波的振动方程声波是由介质中分子振动引起的机械波,声波的振动方程可以根据声源的特性来确定。
如果是简谐波源,声波的振动方程为:p(x, t) = P * cos(kx - ωt)其中,p(x,t)表示声音压强的变化,P是声压的振幅,k是声波的波数,ω是声波的角频率。
3.光波的振动方程光波是由电磁波产生的波动,在真空中传播的光波具有简单的振动方程。
光波的振动方程为:E(x, t) = E0 * cos(kx - ωt + φ)其中,E(x,t)表示光的电场强度的变化,E0是光场的振幅,k是光波的波数,ω是光波的角频率,φ是相位差。
对于一些特殊的波源,振动方程可能会有一些修正。
例如,对于渐变折射率或介质散射的波源,振动方程可以通过复杂的数学方程来描述。
在量子力学中,波动方程描述了微观物体的波粒二象性,波源的振动方程则是以波函数的形式给出。
总之,波源的振动方程是描述波源振动状态的数学公式。
具体的振动方程形式取决于波源的性质和所研究的波动类型。
以上所介绍的只是一些常见的波源振动方程形式,实际情况还需要根据具体的问题来确定振动方程。
声波

声波声波发声体的振动在空气或其他物质中的传播叫做声波。
声波借助各种介质向四面八方传播。
声波一种纵波,是弹性介质中传播着的压力振动。
但在固体中传播时,也可以同时有纵波及横波。
声波(Sound Wave或Acoustic Wave)是声音的传播形式。
声波是一种机械波,由物体(声源)振动产生,声波传播的空间就称为声场。
在气体和液体介质中传播时是一种纵波,但在固体介质中传播时可能混有横波。
人耳可以听到的声波的频率一般在20赫兹至20000赫兹之间。
声波可以理解为介质偏离平衡态的小扰动的传播。
这个传播过程只是能量的传递过程,而不发生质量的传递。
如果扰动量比较小,则声波的传递满足经典的波动方程,是线性波。
如果扰动很大,则不满足线性的声波方程,会出现波的色散,和激波的产生。
种类鉴定按频率分类,频率低于20Hz的声波称为次声波;频率20Hz~20kHz的声波称为可听波;频率20kHz~1GHz 的声波称为超声波;频率大于1GHz的声波称为特超声或微波超声。
声波与正弦波、冲击波、纵波的联系与正弦波的关系正弦波是最简单的波动形式。
优质的音叉振动发出声音的时候产生的是正弦声波。
这是声波的震荡波形。
正弦声波属于纯音。
任何复杂的声波都是多种正弦波叠加而成的复合波,它们是有别于纯音的复合音。
正弦波是各种复杂声波的基本单元。
与冲击波的区别请注意,声波不是冲击波,声波前进的过程是相邻空气粒子之间的接力赛,它们把波动形式向前传递,它们自己仍旧在原地振荡,也就是说空气粒子并不跟着声波前进!同样,在语音研究中要区分气流与声波,它们是两回事。
在发音器官里,声带、舌尖或小舌的颤动,以及辅音噪声的形成等,都离不开气流的作用,但是气流不是声波的代名词。
所谓“*浊音气流”、“*清音气流”的说法似乎包含了极其含混的意思。
另外,即使没有其他声源体的作用,空气粒子总是在做无规则的震荡,或者说它们总是在骚动,它们激发起微弱的“白噪声”。
绝对静寂的大气空间是不存在的。
4_2_2波动方程、波的能量、声波

§2.4 波动方程与波速
一、波动方程 简谐波的波函数为: 简谐波的波函数为: y(x,t)=Acosk(ut-x) 2 y y = k 2u2 A sin k(ut x) = kuAsin k(ut x) 2 t t y 2 y = kAsin k(ut x) = k 2 A sin k(ut x) x x 2 2 2 y 2 y =u --- 平面波的波动方程 平面波的波动方程 2 2 t x 其通解为 y = f1 ( x + ut ) + f 2 ( x ut ) --- 平面波函数 平面波函数 u 为波速
w = w
k
W V
p
1 y = E 2 x
2
2
+ w
p
1 y 1 y = ρ + E t x 2 2
2
3.能量密度 能量密度 w = w
k
+ w
p
1 y 1 y = ρ + E t 2 2 x
E ρ
2
2
棒中纵波速度 u =
E = ρu 2
1 2 y w p = ρu 2 x
1 y = ρ t 2
2
2.势能密度 势能密度
--- 与弹性(形变)有关 与弹性(形变)
考虑一棒的线变, 考虑一棒的线变, 棒长: 截面: 棒长:l ,截面:S 两端拉力: 两端拉力:由0 → F 相应形变:增至 , 应变。 相应形变:增至l,应力 ∝ 应变。
F ES l =E F= l = kl S l l 1 2 k (l ) 势能: W p = 势能: 2
声波的基本性质及传播规律
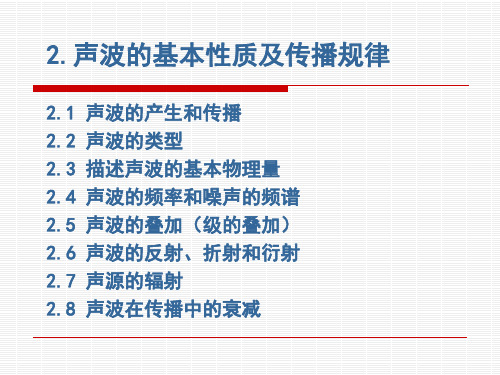
垂直于传播 相互平行 方向的平面 的直线 以任何值为 由声源发出 半径的球面 的半径线 同轴圆柱面 线声源发出 的半径线
球面声波
点声源
p r, t
p pA
pA cos(t kr ) r
柱面声波
线声源
2 cos(t kr ) kr
2.3 描述声波的基本物理量
声压:压强的改变量(p′- p0)(Pa)
DI是指向性指数,
DI 10 lg R
Lp LW 20lg r 11 DI
r2 L 20 lg r1
2.7.2 点声源在半自由空间中的辐射
某一方向θ上的声压级计算
上次课内容回顾
声压和声压级、声强和声强级、声功率和声功率级
声压级的叠加
Lp 10lg(10
i 1
n
0.1Lpi
)(dB)
3 2 1 0
81dB、 72dB 、 78dB、81dB
0
5
10
15
分贝相加曲线
上次课内容回顾
声压级的相减
熟悉倍频程的 概念和划分
0.1Lp 2
Lp1 10lg(10
2.声波的基本性质及传播规律
2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 声波的产生和传播 声波的类型 描述声波的基本物理量 声波的频率和噪声的频谱 声波的叠加(级的叠加) 声波的反射、折射和衍射 声源的辐射 声波在传播中的衰减
2.1 声波的产生和传播
声源振动
纵波和横波 声场
弹性媒介振动
Lp(dB)
f2 n 2 f1
Lp(dB) Lp(dB)
离散谱
f(Hz)
连续谱
波动方程的三种表达式

波动方程的公式分为正弦和余弦,其中正弦表达式为Y=Asin(ωt-kz+φ),余弦表达式为为Y=ACOS[ω(t-kz)+φ],其中z代表位移,φ是初相位。
波动方程也称波方程,是一种描述波动现象的偏微分方程,它通常表述所有种类的波,例如声波,光波和水波等,在不同领域都有涉及,例如声学,电磁学,和流体力学等。
波动方程就是描述波动现象的偏微分方程,它的物理意义就太宽泛了。
不过波动方程一个很重要的性质是传播速度有限(不像热传导方程)。
电磁场的运动方程是波动方程这说明电磁相互作用只能以有限的速度传播(光速c),而没有瞬时的作用(即超距作用)。
这是导致狭义相对论建立的一个重要思想。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
固体中的声波方程 11.固体的基本弹性性质 要建立固体中声波方程,首先必须了解固体的基本弹性性质,当固体受到外力作用时,体内就产生形变,一般用物理量应变来描述,由于固体的弹性性质体内各部分之间就产生互相作用力,而这种力是通过它们的界面起作用的具有面力的性质,一般用物理量-应力来描述。固体中应变与应力的关系远比流体复杂得多,因此需要详细分析。 1.1 固体中的应变分析 我们考察固体中某一点 A ,其坐标为( x,y,z),由于某种原因它产生了位移,它在x,y,z方向的位移分量分别为ξ,η,ζ,设与它相邻的 C 点坐标为( x+dx, y+dy ,z+dz ) ,它的位移相应为ξ+dξ,η+dη,ζ+dζ。利用泰勒级数展开可得 A 与 C 点的位移差为:
式1 从式1可见,固体中的形变可用如下九个应变分量来描述
式2 为了简化分析采用如下符号: 固体中的声波方程 2式3 我们用图 1所示的二维模型来考察固体的形变。取原来的一小
方体元 ABCD 经形变后成为菱形A’B’C’D ' 。从图可以清楚看到, εxx 就是代表长度为 dx 的线段沿 x 轴的简单的相对“伸长” , 称为 x 方向的伸长应变。εyy同样为长度为dy的线段沿 y 轴相对“伸长” , εzz为沿 z 轴的相对“伸长”。从图还可看到,形变的另一特征是小体元形变成菱形,其两棱边的夹角发生了变化。
图1 固体中的声波方程
3这一夹角的变化就代表了小体元的切形变大小。考虑到形变量是微量.所以 x方向棱边绕 Oz轴的旋转角为:x¶¶=»hqq11tan y 方向棱边绕 Oz轴的旋转角为:y¶¶-=»xqq22tan 于是,yxxyeeqq==-21就是小体元在 xOy平面的切形变,称为xOy平面的切应变.同样从图可知yx¶¶+¶¶=-xhqq21。 这就是对角线 AC 转动角度的 2 倍,因而Ωz就相当于小体元绕 z 轴的旋转。类似地可以指出Ωy为绕y轴的旋转,Ωx为绕 x 轴的旋转。显然这些旋转量对体元的形变没有贡献,类似地还可以得到yOz平面的切应变zyyzee=以及xOz 平面的切应变zxxzee=。根据以上分析可知,描述固体中的形变可以不必用式1中的 9 个应变分量,而只要用如下的 6 个: 3 个伸长应变εxx ,εyy ,εzz, 3 个切应变
zxyzxyeee,,
。
1.2 固体中的应力分析 我们还是从固体中割出一个小体元 dV 来进行分析,当固体形变时该小体元将受到周围相邻部分力的作用,我们称作用在小体元单位表面上的力为应力,由于固体能产生切形变,所以作用在小体元上的应力,除了像流体一样有法向应力外(流体中用压强表示)还存在方向与作用表面相切的切应力,从图 2 可以看到,在所取的小体元的表面上一般存在 9 个应力分量, 固体中的声波方程
4 图2 其中 Txx表示作用在x面(与x轴垂直的表面)上方向指向 x 轴的应力,Txy表示作用在x面方向指向 y 轴的应力,以此类推。我们用符号Tij ( i ,j =x,y ,z )来表示应力,那么当 i=j 时它表示法向应力,当 i ≠j 时表示切应力。稍加证明还可指出,一般这 9 个应力分量并不完全独立,它们具有对称性,即 Tij= Tji。因此实际上只要用 6 个应力分量就可完全确定固体的应力特性。为此我们再来观察一下图2的小体元,由于各表面受有切应力,所以它们对中心轴将产生力矩,例如绕 x 轴的力矩等于 dzdxdyTdydxdzTdMzyyzx)()(-= 固体中的声波方程 5 根据动量矩守恒定律,该力矩应等于小体元绕 x 轴的转动惯量乘以角加速度。而转动惯量等于])2()2[(22dzdydxdydz+r ,因为 dx 为微量,显然转动惯量为5级微量,它与3级微量力矩相比可以忽略,于是可近似得:xdM=0,所以,0)()(=-dzdxdyTdydxdzTzyyz,即zyyzTT=。同理可得yxxyzxxzTTTT==,。 1.3 广义虎克定律 从上面分析已知,对于固体媒质可以用六个应变分量来描述形变,用六个应力分量来描述应力,而应变与应力之间是有关系的.假设我们研究的是产生小形变情形,一般讲应变与应力应该具有线性关系,而且所有的应变分量对每一应力分量都应有贡献,所以每一应力应该是 6 个应变分量的线性函数,它们的一般关系可表示成如下形式:
式4 式中 Cij(i,j = 1 , 2 , 3 , 4 , 5 , 6 )称为弹性系数,它决定于固体媒质的弹性性质。式4就是弹性力虎克定律在固体中的推广,称为广义虎克定律。从式中可以看到,固体的弹性性质比流体要复杂得多,一般具有 36 个弹性系数.但是实际上这 36 个系数不是完全独立的,因为弹性能是应变的单值函数,所以可以证明弹性系数具有固体中的声波方程 6对称性 C ij= C ji,这样独立的弹性系数就减少到 21 个,对于具有对称性的晶体,独立的弹性系数还可减少,例如对于三角系晶体如石英,铝酸锂等,弹性系数减少到 6 个,六角系晶体如氧化锌,硫化锡等,弹性系数减少到 5 个,而立方形晶体像砷化稼等减少到 3 个,对于各向同性固体像金属、玻璃等弹性系数更可减少为 2 个。 对于各向同性固体,广义虎克定律可简化为:
xyxyzxzxyzyzzzzzyyxxzzyyzzyyxxyyxxzzyyxxxx
TTTTTTmemememeeeelmeeeelmeeeel===+++=+++=+++=2)(2)(
2)(
式5
这里,λ,μ称为拉密常数,它们与各弹性系数Cij之间的关系为 λ=C12 =C13 =C21= C23=C31= C32
μ= C44= C55 =C66 =1/2(C11 -C12)
λ+2μ= C11 =C22 =C33。 其他弹性系数全部为0。μ也称为切变弹性系数。它的物理意义是比较明显的,表示单位切应变对应的切应力数值。 1.4 拉密常数与杨氏模量、泊松比的关系 对于各向同性固体虽然拉密常数中的切变弹性系数μ的物理意义是明确的,然而λ的含义就不十分清楚,为此人们常常喜欢采用另外两个物理意义比较明确的弹性常数 ― 杨氏模量E 和泊松比σ,来表示其弹性性质。下面我们就来建立这些量之间的联系。我们还是研究一下图 2 的小体元.假如此小体元只在 x 方向受到法向应力 固体中的声波方程 7Txx的作用,那么在x方向的伸长应变与法向应力成正比,比例系数为1/E,即ETxxxx='e,E为杨氏模量。如果只在 y 方向受到法向应力,
那么除在 y 方向有伸长应变ETyyyy='e外,同时在 x 方向也会形起横向缩短应变yyxxsee-=''。这里引入负号表示缩短的意思,它的比例系数σ称为泊松比。类似地可以考虑,只在 z 方向作用法向应力Tzz,
那么它除在 z 方向产生伸长应变ETzzzz='e外,还在 x 方向产生缩短
应变,zzzzxxETsese-=-='''。 现在假设这一小体元同时受到三个法向应力Txx,Tyy, Tzz的作用,那么在 x 方向的总相对伸长显然应该等于: )]([1''''''zzyyxxxxxxxxxxTTTE+-=++=seeee 同理可得y、z方向的总相对伸长为: )]([1''''''zzxxyyyyyyyyyyTTTE+-=++=seeee
)]([1''''''zzyyzzzzzzzzzzTTTE+-=++=seeee 上面三式可改写成:
zzyyzzzzzzxxyyyyzzyyxxxxTTTETTTETTTEssessesse--=--=
--=
求解上述方程组可得: 固体中的声波方程
8zzzzyyxxzzyyzzyyxxyyxxzzyyxxxx
EETEETEETeseeessseseeessseseeesss)1()()21)(1()1()()21)(1()1()()21)(1(++++-+=
++++-+=++++-+= 式6 比较式5与式6可得: )1(2)21)(1(smsssl+=-+=E
E
式7
由此可见,对于各向同性固体完全可以用杨氏模量E和泊松比σ,来表征其弹性性质。例如对一般金属杨氏模量约在( 7 - 20 ) ×1010N / m2 范围,而泊松比约为0.25- 0. 40。 2.固体中声波的传播 上面我们确立了固体中应变与应力的关系,如果再利用固体中的媒质运动方程就可建立用单一参量表示的声波方程。对于各向异性的固体,由于应变与应力关系的复杂性,可以预料声波的传播特性也是十分复杂的。为了揭示固体中最基本的声波传播特性,我们把问题尽量简化,仅限于讨论各向同性媒质。 为了导出固体中的媒质运动方程,我们再来观察一下图2中所示的小体元。先来研究一下小体元在x方向的受力情形,从图中可以看出,作用在该小体元x方向的分力由如下三部分组成: (1) 作用在垂直于x轴表面的x方向的分力
