对顶角同位角内错角同旁内角
同位角、内错角、同旁外角、垂线
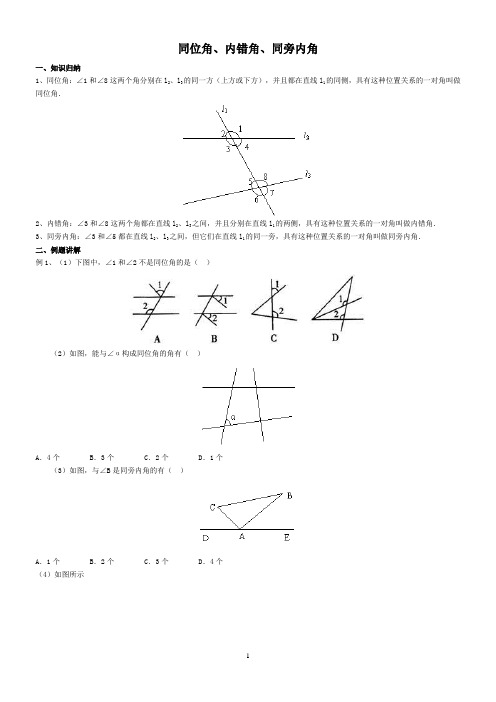
同位角、内错角、同旁内角一、知识归纳1、同位角:∠1和∠8这两个角分别在l2、l3的同一方(上方或下方),并且都在直线l1的同侧,具有这种位置关系的一对角叫做同位角.2、内错角:∠3和∠8这两个角都在直线l2、l3之间,并且分别在直线l1的两侧,具有这种位置关系的一对角叫做内错角.3、同旁内角:∠3和∠5都在直线l2、l3之间,但它们在直线l1的同一旁,具有这种位置关系的一对角叫做同旁内角.二、例题讲解例1、(1)下图中,∠1和∠2不是同位角的是()(2)如图,能与∠α构成同位角的角有()A.4个B.3个C.2个D.1个(3)如图,与∠B是同旁内角的有()A.1个B.2个C.3个D.4个(4)如图所示①AB与BC被AD所截得的内错角有_____________;②DE与AC被AD所截得的内错角有_____________;③DE与AC被BC所截得的同位角有_____________;④∠5、∠7是_____________被_____________直线所截得的_____________角;⑤∠1、∠4是_____________被_____________所截得的_____________角;⑥∠B、∠7是_____________被_____________所截得的_____________角.(5)如图,直线AB、CD、EF两两相交,请指出∠1与其它有标号的角是什么角?例2、(1)如图,下列判断错误的是()A.∠1和∠2是同旁内角B.∠3和∠4是内错角C.∠5和∠6是同旁内角D.∠5和∠8是同位角(2)如图,指出∠1、∠2、∠3、∠4、∠5中是同位角的有__________对,是内错角的有__________对,是同旁内角的有__________对.一、选择题1、如图所示,∠1和∠2是同位角的是()A.②③B.①②③C.④D.①④2、∠1与∠2不是内错角的是()3、如图所示,直线AB,CD,EF两两相交,图中共有同旁内角()A.1对B.3对C.6对D.12对4、如图所示,有以下四种说法:①∠1和∠4是同位角;②∠3和∠5是内错角;③∠2和∠6是同旁内角;④∠2和∠5是同位角,其中正确的说法有()A.1个B.2个C.3个D.4个5、如图所示,AB,BE被AC所截,下列说法不正确的是()A.∠1与∠2是同旁内角B.∠1与∠ACE是内错角C.∠B与∠4是同位角D.不能得到内错角∠1与∠3二、填空题6、如图所示,∠1和∠2是两条直线____________与____________被第三条直线____________所截的____________角;∠5和∠6是两条直线____________与____________被第三条直线____________所截的____________角;∠2和∠6是两条直线____________与____________被第三条直线____________所截的____________角.7、如图所示,∠ABD的同位角有____________,内错角有____________,同旁内角有____________;∠BGH的同位角有____________,内错角有____________,同旁内角有____________.8、如图所示,直线AB,CD被BD所截构成∠3和__________是内错角,AD,BC被BD所截构成的∠1和∠2是___________角,AD,BC被AB所截构成的∠5和∠ABC是___________角,∠6和∠ABC是____________角.三、综合题9、如图所示,∠1和∠E,∠2和∠3,∠3和∠E都是什么角,它们分别是哪两条直线被哪一条直线所截得的?10、如图所示,平行直线EF,MN被相交直线AB,CD所截,请问图中有多少对同旁内角?垂线一、知识归纳1、垂直:当两条直线所有的角为90°时,那么这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.如图,AB与CD相交于O,当交角90°时,称AB与CD垂直,记作AB⊥CD于O. 其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.两直线垂直的位置关系是用角来刻画的.2、在同一平面内,过一点有且只有一条直线与已知直线垂直.3、垂线段最短.4、直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.注意:垂线段:是一个几何图形;距离:是一个数量,这个数量是垂线段的长度.5、正确理解“垂线”、“垂线段”、“两点间距离”、“点到直线的距离”这些相近而又相异的概念.如上图(1)AB与CD相交,当交角90°时,称AB与CD垂直,其中的一条直线叫做另一条直线的垂线;如图(2)过P到这条直线所引的直线中,点P与垂足E之间的线段PE叫做垂线段;P到垂足E之间的距离叫点到直线的距离;如图3,点M和点N之间的线段的长度叫两点间距离.二、例题讲解例1、(1)下列条件中,位置关系互相垂直的是()A.相邻两角的角平分线B.互为对顶角的两角的角平分线C.互为邻补角的两角的角平分线D.互为补角的两角的平分线(2)甲、乙、丙、丁四个同学在判断时针与分针在某一时刻是否互相垂直时,有下列几种说法,其中完全正确的是()A.甲说3点和3点半B.乙说6点一刻和6点3刻C.丙说9点和12点3刻D.丁说3点和9点例2、如图,根据下列语句画图:(1)过点P画射线AM的垂线,Q为垂足;(2)过点P画射线BN的垂线,交射线BN反向延长线于Q点;(3)过点P画线段AB的垂线,交线段AB延长线于Q点.例3、如图,∠BAC=90°,AD⊥BC,则下列的结论中正确的是个数是()①点B到AC的垂线段是线段AB②线段AC是点C到AB的垂线段③线段AD是点D到BC的垂线段④线段BD是点B到AD的垂线段A.1 B.2 C.3 D.4例4、(1)如图,直线AB⊥CD于点O,点M是OC上的一个定点,点P是直线AB上的一个动点,则()A.PM>OM B.PM<OMC.PM≥OM D.PM≤OM(2)到直线l的距离等于2cm的点有()A.0个B.1个C.2个D.无数个(3)直线l上有A、B、C三点,直线l外有一点P,若PA=4cm,PB=3cm,PC=2cm,那么P点到直线l的距离()A.等于2cm B.小于2cmC.不大于2cm D.大于2cm而小于3cm(4)如图,AD⊥BD,BC⊥CD,AB=acm,BC=bcm,则BD的取值范围是()A.小于bcmB.大于acmC.大于acm或小于bcmD.大于bcm且小于acm例5、(1)如图,直线AB与CD相交于点O,EO⊥AB于O,则图中∠1与∠2的关系是___________.(2)如图,将一张长方形的白纸折叠,使BD折到BD′处,BE折到BE′处,并且BD′与BE′在同一直线上,那么AB与BC 的位置关系是__________.(3)过一个钝角的顶点分别作这个角两边的垂线,若这两条垂线的夹角为40°,则此钝角为()A.140°B.160°C.120°D.110°例6、(1)如图,点O为直线AB上一点,ON平分∠BOC,OM⊥ON,试说明OM平分∠AOC的理由.(2)如图,AB⊥BC于B,AB=4,BC=3,AC=5,求B到AC的距离.一、选择题1、P为直线l上一点,Q为l外一点,下面画图一定可能的是()A.由P画l的垂线过Q点B.由Q画l的垂线过P点C.连接PQ使PQ⊥l D.过P或Q作l的垂线2、已知直线l外一点P,则点P到直线l的距离是指()A.点P到直线l的垂线的长度 B.点P到l的垂线C.点P到直线l的垂线段的长度 D.点P到l的垂线段3、已知OA⊥OC,∠AOB∶∠AOC=2∶3,则∠BOC的度数是()A.30°B.150°C.30°或150° D.以上都不对4、点P为直线l外一点,点A,B,C在直线l上,若PA=4cm,PB=5cm,PC=6cm,则点P到直线l的距离是()A.4cm B.小于4cmC.不大于4cm D.5cm5、如图所示,OA⊥BC,OM⊥ON,则图中互余的角有()A.1对B.2对C.3对D.4对6、如图所示,∠PQR=138°,SQ⊥QR,QT⊥PQ,则∠SQT等于()A.42°B.64°C.48°D.24°二、填空题7、如图所示,计划把池中的水引到C处,可过C点引CD⊥AB于D,然后沿CD开渠,可使所在的渠道最短,说明这种设计的依据是__________________.8、画图并回答:如图所示,已知点P在∠AOC的边OA上.(1)过点P画OA的垂线交OC于点B;(2)画点P到OB的垂线段PM;(3)指出上述所作的图中,线段___________的长表示P点到OB边的距离;(4)比较PM与OP的大小,并说明理由.三、综合题9、如图所示,O是直线AB上一点,OF,OC,OE是射线,OE⊥OF,若∠BOC=2∠COE,∠AOF比∠COE的4倍小8°,求∠EOC的度数.10、如图所示,∠1和∠2有公共顶点,且∠1的两边与∠2的两边分别垂直,又∠1∶∠2=5∶13,求∠1,∠2的度数.11、如图所示,一辆汽车在直线形的公路AB上由A向B行驶,M,N是分别位于AB两侧的村庄.(1)设汽车行驶到公路AB上点P的位置时,距离村庄M最近;行驶到点Q的位置时,距离村庄N最近,请在图中的公路上分别画出P,Q的位置(保留画图痕迹);(2)当汽车从A出发向B行驶时,在公路AB的哪一段路上距离M,N两村越来越近?在哪一段路上离N村越来越近,而离村庄M却越来越远?(分别用文字表达你的结论,不必证明)。
5.1.3同位角-内错角-同旁内角

同位角
3
1
∠2和∠6;∠3和∠7 图中的同位角还有哪些? ; ∠ 4和 ∠ 8
归纳总结
变式图形:图中的∠1与∠2都是同位角.
2
1
1
2
1 2
1
2
图形特征:在形如字母“F”的图形中有同位角.
典型例题 新知:同位角、内错角、同旁内角的概念
【例1】如图5-1-41,直线a,b被直线c所截,与∠1是同 位角的是( B ) A. ∠2 B. ∠3 C. ∠4 D. ∠5
归纳:公共边就是“截线”
练一练
2
A
4 3
E
1
根据图形按要求填空: (1)∠1与∠2是直线 AB 和 EC 被直 线 BD 所截而得的 同位角 . (2) ∠3与∠4是直线 AB 和 EC 被直 线 AC 所截而得的 内错角 .
B
C
D
能力挑战: 看图填空
A E
2 1 3D4来自BFC
(2) ∠1与∠2是___ ED与___ BF 被____ AB 所截形成
E
1 2 G 3 5 6 H 7 F
B 如图:直线AB、CD与
A C
4
8
EF相交,我们就称为直 线AB、CD被直线EF所 截。三条直线相交构成 如图的8个角。其中AB、 D CD叫做被截线,EF叫 做截线。
简称“三线八角”
一、同位角的概念 活动1 观察∠1与∠5的位置关系 : ①在直线EF的同旁(右边) ②在直线AB、CD的同一侧(上方)
试一试:
根据图形按要求填空: (1)∠1与∠2是直线 AB 和 DE 被直线 BC 所 截而得的 同位角 . (2) ∠1与∠3是直线 AB 和 DE 被直 线 BC 所截而得的 内错角 .
_同位角、内错角、同旁内角

6
3 2
B D
C
1 F
观察∠3和∠6:
各有一边在同一直线上 E A 5 4 C 8 6 3 2 F D 7 B
6
3
1
观察∠3和∠6:
E A 5 4 C 8 6 3 2 F 7 B
6
3
1
D
观察∠3和∠6:
E A 5 4 8 6 3 2 B D 7
6
3
C
1
观察∠3和∠6:
6 3
同旁内角
在截线同旁,夹
4.点到直线的距离的定义
a b O
P
直线外一点到这条直 线的垂线段的长度,叫做 点到直线的距离。
A3 A1
A2
O
B3
B2 B1
l
1. 邻补角的性质
邻补角互补
C
2.对顶角的性质: 对顶角相等
3、垂线的性质(1)
B 2 O ( ( ) 1 3 ) 4 D A
在同一平面内,过一点有且只有一条 直线与已知直线垂直。 4、垂线的性质(2)
AE BC (1) ∠ 1与∠ C是两条直线___、___ CD 同位 被第三条直线___所截构成的___角 ; AE BC (2)∠ 2与∠ B是两条直线___、 ______ AB 所截构成的___角; 内错 被第三条直线______
D 1 A 2 3
AB (3)∠ BAD与∠ C是两条直线___、 CD BC ___被第三条直线___所截构成的
E
2 1 3 4
A
B D
6 5 7 8
两条直线AB和CD之间 第三条直线EF的两侧
问:图中还有哪些内错角? 答:还有∠ 4和∠ 6。
C
F
观察∠3和∠5两角, 观察图形结构形如字母 哪一个?
同位角内错角同旁内角

一、创设情景
1.1 同位角,内错角,同旁内角 l
a
直线a、 被直线 所截, 被直线l所截 直线 、b被直线 所截 则称a、 为两直线 为截线 为两直线, 则称 、b为两直线 l为截线
b
1.1 同位角,内错角,同旁内角
直线a、 被直线 所截,有几对对 被直线l所截 直线 、b被直线 所截 有几对对 顶角,它们分别是哪些角 它们分别是哪些角? 顶角 它们分别是哪些角
4
内错角还有∠ 与 内错角还有∠3与∠5。 。
6
(Z型) 型
二、探索交流 变式图形:图中的∠ 与 变式图形:图中的∠1与∠2都是内错角 都是内错角
图形特征:在形如“ 的图形中有内错角 的图形中有内错角。 图形特征:在形如“Z”的图形中有内错角。
二、类比交流 来看, 处于哪个位置? 从直线 l 来看,∠4与∠5处于哪个位置? ∠4与∠5处于直线 l 的同一侧
2、根据地图显示填空: 、根据地图显示填空:
交通指南
学校与游乐场所在的角 形成一( 形成一( 同位角 )角 学校与超市所在的角形 成一对( 成一对( 同旁内角 )角 学校与飞机场所在的角 形成一对( 形成一对( 内错角 )角
游乐 场
超市
学校 学
解 飞机场 人
放
路
马 民 路 鞍 池 路
练习
如图,直线 截直线 截直线b,直线c所得的同位角有 如图,直线a截直线 ,直线 所得的同位角有 ______对,它们是 4 对 ∠1与∠3, ∠2与∠4, ∠5与∠7, ∠6与∠8 与 , 与 , 与 , 与 ______________________________________________; 与 , 与 内错角有______对,它们是 ∠2与∠7, ∠3与∠6 内错角有 2 对 它们是______________________; 同旁内角有_____对,它们是 同旁内角有 2 对 它们是______________________。 。 2与 3, 6与 ∠ 2与 ∠ 3, ∠ 6与 ∠ 7 c b 1 2 5 6 3 7 4 8
易错拔尖:同位角、内错角、同旁内角(解析版)

易错拔尖:同位角、内错角、同旁内角(解析版)➢ 易错点1.如图所示,找出图中所有的与∠1是同位角、内错角和同旁内角的角.思路导引:分四种情况讨论,(1)当AB 、BC 被AC 所截时,∠1和∠7是同旁内角;(2)当AB 、CD 被AC 所截时,∠1和∠2是内错角;(3)当AC 、BD 被AB 所截时,∠1和∠6是同旁内角;(4)当AC 、BC 被AB 所截时,∠1和∠ABC 是同旁内角.解:∠1没有同位角,∠1的内错角有∠2,∠1的同旁内角有∠6、∠ABC 、∠7.易错总结:解答此题时,常常误认为∠1和∠3是同位角,∠1和∠4是同旁内角等,事实上这两对角不是由两直线被第三条直线所截形成的,这是判定同位角、内错角、同旁内角前提条件.误点警示:不注意概念的运用,而导致识别错误➢ 拔尖角度角度1 利用“三线八角”的定义识别相关角1.如图1、图2中的∠1和∠2,∠3和∠4分别是哪两条直线被哪一条直线所截形成的?它们各是什么位置关系的角?思路引领:根据同位角,内错角,同旁内角的定义进行判定即可得出答案. 解:图1中,∠1和∠2分别是直线AB ,CD 被直线BD 所截形成的内错角; ∠3和∠4分别是直线AD ,BC 被直线BD 所截形成的内错角; 图2中,∠1和∠2分别是直线AB ,CD 被直线BC 所截形成的同位角; ∠3和∠4分别是直线AB ,BC 被直线AC 所截形成的同旁内角.总结提升:本题主要考查了同位角,内错角,同旁内角的定义,熟练掌握同位角,内错角,同旁内角的定义进行判定是解决本题的关键.D ABC 14325678角度2 利用“三线八角”的定义画示意图2.(2020春•江城区期末)两条直线被第三条直线所截,∠1和∠2是同旁内角,∠3和∠2是内错角.(1)根据上述条件,画出符合题意的示意图;(2)若∠1=3∠2、∠2=3∠3,求∠1,∠2的度数.思路引领:(1)根据内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,画出图形.(2)根据已知角的关系确定∠1=9∠3,再根据图形中∠1和∠3组成邻补角互补可得方程,再解即可.解:(1)如图所示:(2)∵∠1=3∠2、∠2=3∠3,∴∠1=9∠3,∵∠1+∠3=180°,∴9∠3+∠3=180°,∴∠3=18°,∴∠1=162°,∠2=54°.总结提升:此题主要考查了三线八角,以及角的计算,关键是掌握内错角的边构成“Z“形,同旁内角的边构成“U”形.角度3 利用“三线八角”的定义识别相关角3.如图所示.(1)∠1与∠C,∠2与∠B,∠3与∠C各是什么角,是哪两条直线被哪一条直线所截得的?(2)∠3的内错角有哪些?(3)写出直线DE,BC被AB所截得的同旁内角,直线DE,BC被EF所截得的同旁内角.思路引领:(1)在截线的同旁找同位角;(2)根据内错的概念找到即可;(3)由同旁内角的概念解答即可.解:(1)∠1与∠C是直线DE、BC被直线AC所截形成的同位角,∠2与∠B是直线DE、BC被直线AB所截形成的同位角,∠3与∠C是直线DF、AC被直线BC所截形成的同位角;(2)当直线DE与BC被DF所截时,∠3与∠EDF是内错角;当直线AB和BC被EF所截时,∠3与∠ADF是内错角;(3)直线DE,BC被AB所截得的同旁内角有∠B与∠BDE,直线DE,BC被EF所截得的同旁内角∠DEF与∠BFE.总结提升:本题主要考查学生对内错角与同旁内角的掌握情况,观察时,关键要抓住各类角的特征,这也是学生易错的地方,并且还容易出现漏解的情况.角度4 利用“三线八角”的特征说明相关角的关系4.如图,若∠1=∠B,那么∠2与∠B有何数量关系?并说明理由;若∠4+∠C=180,那么∠3与∠C有何数量关系?并说明理由.思路引领:根据“同位角相等,两直线平行”推知DE∥BC,则由“两直线平行,同旁内角互补”得到∠2+∠B=180°;由“同旁内角互补,两直线平行”和“两直线平行,同位角相等”得到∠3=∠C.解:∠2+∠B=180°.理由如下:∵∠1=∠B,∴DE∥BC,∴∠2+∠B=180°.∵∠4+∠C=180,∴DE∥BC,∴∠3=∠C.总结提升:本题考查了平行线的判定与性质.平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.5.如图,有四条互相不平行的直线l1、l2、l3、l4所截出的八个角.请你任意选择其中的三个角(不可选择未标注的角),尝试找到它们的关系,并选择其中一组予以证明.思路引领:根据三角形的外角和为360°,三角形的内角和为180°以及三角形外角和定理即可写出三个角之间的数量关系.解:如∠2+∠4+∠6=360°,∠1+∠5+∠7=180°,∠2=∠5+∠7,∠3=∠1+∠8,已知如图:有四条互相不平行的直线l1、l2、l3、l4所截出的八个角,求证:∠1+∠5+∠7=180°,证明:∵∠DAC+∠7+∠5=180°,又∵∠1=∠DAC,∴∠1+∠5+∠7=180°.总结提升:此题主要考查了对顶角的性质以及三角形的内角和定理,正确的应用三角形内角和定理是解决问题的关键.角度5 利用“三线八角”的定义探究角的对数6.(1)如图1,两条水平的直线被一条竖直的直线所截,同位角有对,内错角有对,同旁内角有对.(2)如图2,三条水平的直线被一条竖直的直线所截,同位角有对,内错角有对,同旁内角有对.(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有对,内错角有对,同旁内角有对.(用含n的式子表示)思路引领:根据同位角是两个角都在截线的同旁,又分别处在被截的两条直线同侧的位置的角,内错角是两个角都在截线的两侧,又分别处在被截的两条直线中间的位置的角,根据同旁内角是两个角都在截线的同旁,又分别处在被截的两条直线中间的位置的角,可得答案.解:(1)如图1,两条水平的直线被一条竖直的直线所截,同位角有4对,内错角有2对,同旁内角有2对.(2)如图2,三条水平的直线被一条竖直的直线所截,同位角有12对,内错角有6对,同旁内角有6对.(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有2n(n ﹣1)对,内错角有n(n﹣1)对,同旁内角有n(n﹣1)对,故答案为:4,2,2;12,6,6;2n(n﹣1),n(n﹣1),n(n﹣1).总结提升:本题考查了同位角、内错角、同旁内角,解答此类题确定三线八角是关键,可直接从截线入手.对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义.角度6 复杂图形中找出已知角的同位角,内错角和同旁内角.7.(2021春•长白县期中)如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是(填序号).思路引领:准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.解:①∠A与∠1是同位角,此结论正确;②∠A 与∠B 是同旁内角,此结论正确; ③∠4与∠1是内错角,此结论正确; ④∠1与∠3不是同位角,原来的结论错误; 故答案为:①②③.总结提升:此题主要考查了同位角、内错角、同旁内角,在复杂的图形中识别同位角、内错角、同旁内角时,应当沿着角的边将图形补全,或者把多余的线暂时略去,找到三线八角的基本图形,进而确定这两个角的位置关系8.如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动后,到达终点角.跳动时,每一步只能跳到它的同位角、内错角或同旁内角的位置上.如从起始位置∠1跳到终点位置∠3的路径有跳径1:∠1→同旁内角∠9→内错角∠3;跳径2:∠1→内错角∠12→内错角∠6→同位角∠10→同旁内角∠3等.(1)写出从∠1到∠8的一条路径;(2)从起始位置∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点位置∠8? (3)写出从起始位置∠1跳到终点位置∠8的路径,要求跳遍所有的角,且不能重复.思路引领:首先根据已知条件找出角与角之间的关系,再根据“同位角、内错角、同旁内角”的定义进行判断,找到正确的游戏路线即可. 解:(1)∠1→同旁内角∠9→内错角∠8(路径不唯一);(2)能.∠1→同位角∠10 →内错角∠5→同旁内角∠8;(3)∠1→同旁内角∠9→同旁内角∠2→内错角∠10→同旁内角∠3→同旁内角∠4→内错角∠11→同旁内角∠5→同旁内角∠6→内错角∠12→同旁内角∠7→同旁内角∠8(路径不唯一).总结提升:本题考查同位角、同旁内角与内错角,熟练掌握同位角、同旁内角与内错角的定义是解答本题的关键.。
5.1.3同位角、内错角、同旁内角PPT

E
A C
21
B
34
65
D
78
F
【问题二】观察并思考
观察∠3与∠5的位置特点
它们都在截线EF的异侧,并且都位于两 条被截线AB,CD之间.像这样的一对角叫 做“内错角”。
像这样的角还有∠4与∠6,也是一对内错角
A C
E
21
B
34
65
D
78
F
问题与讨论:组成内错角的三条“边线” 看起来像个什么形状或东西?
状像什么?)
问题2:在下面同位角、内错角、同旁内角中任选一对角, 请你看看这对角的四条边与“前提”中的“三线”有 什么关系?
结论:两个角在同一直线上的边所在直线就是 前提中的第三线(即截线)。
初试身手(示范及训练) 例1:如下左图:请指出图中的同旁内角. (提示:请仔细读题、认真看图.)
答:∠1与∠5; ∠4与∠6; ∠1与∠A; ∠5与∠A
∠1和∠5这两个角,一是在截线EF的同旁, 二同是它们在被截两直线AB、CD的同一 方向;像这样的一对角叫做“同位角”。
像这样的角还有那几对?把它说出来
E
21
B
A
34
65
D
C
78
F
问题与讨论:组成同位角的三条“边线” 看起来像个什么形状或东西?
你觉得像个什么?说出你的想法?
同位角----像个字母“F”,(”F”可以翻转、 旋转、变形)
A C
E
21
B
34
65
D
78
F
问题与讨论:组成同旁内角的三条“边线” 看起来像个什么形状或东西?
你觉得像个什么?说出你的想法?
同旁内角----像个字母“U”,(”U”可以 翻转、旋转、变形)
同位角内错角同旁内角

同位角、内错角和同旁内角的结构特征:
l3
2 1 3 4 6 5 7 8
l1
l2
截线 同旁 两旁 同旁 被截线 同侧 之间 之间 结构特征
同位角 内错角 同旁内角
F Z U
(三)归纳小结
1.你能总结一下同位角、内错角、同旁内角分 别具有哪些特征吗? 2.你认为在图形中识别同位角、内错角、同旁 内角的关键是什么?
(二)探索与思考
问题2:三条直线相交可以分为哪些情况?
对三条直线相交按交点的个数分为三种情况:
(1)三条直线交点的个数有一个,即三条直线交于 一点;
l
a b
对三条直线相交按交点的个数分为三种情况:
(1)三条直线交点的个数有一个,即三条直线交于 一点; (2)三条直线交点的个数有两个,即两条直线平行 且被第三条直线所截;
l
(2)两条直线被第三条直线所截.
a b
如图:怎样描述这三条直线的位置关系?
直线AB、CD被EF所截
截线
E
2
1
3 4
B
A
6
被截直线
5
7 8
C
D F
问题:1、观察∠1与∠5的位置关系
同位角:
E
2 1
①在直线EF的同旁
②在直线AB、CD的同一侧 B
1 5
A C
3
6
4
7
8
D F
5
图形特征:在形如“F”的图形中有同位角 。 图中的同位角还有哪些?∠2和∠6;∠3和∠7;
1 1 (4)
同位角
2 1
2 (5)
1 (2)
同位角
2
2 (3)
同位角
b
5.1.3同位角、内错角、同旁内角

∠1与∠2是一对同位角, 是一对同位角 ∠3与∠4是一对内错角, 是一对内错角 ∠2与∠4是一对同旁内角. 是一对同旁内角
D E5
(2)如果把图看成是直线 ) 2 CD,EF被直线AB所截, D,EF被直线AB所截 D,EF被直线AB所截, B C 那么∠ 那么∠1与∠5是一对什么 角?∠4与∠5呢? 与 呢 (3) 哪两条直线被哪一条直线 是一对同旁内角, 所截, ∠1与∠5是一对同旁内角 所截 ∠ 2与∠ 5是同位角 与 是同位角
5.1.3 同位角、内错角、同旁内角 同位角、内错角、
E
两条直线CD EF相交 CD和 相交, 具 两条直线CD和EF相交,能形成 些具有什么关系的角? 有 些具有什么关系的角? 4 3 4 邻 C 1 2 1 补 角 F 关 系 的 角
D
两条直线CD和EF相交, 两条直线CD和EF相交,能形成 CD 相交 些具有什么关系的角? 些具有什么关系的角? 具
能力挑战: 能力挑战: 看图填空
A E
2 1 3
D
4
B
F
C
(1)若ED,BF被AB ED,BF被 所截,则∠1与_____ 所截, ∠2 是同位角。 是同位角。
能力挑战: 能力挑战: 看图填空
A E
2 1 3
D
4
B
F
C
(2)若ED,BC被AF所截, ED,BC被AF所截, 所截 ∠4 是内错角 则∠3与_____是内错角。 _____是内错角。
(2)∵∠ ∠4(已知) ∵∠1=∠ ( ∵∠4+ ∵∠ ∵∠ +∠3=180°(邻补角定义) = ° ∠4=∠2(对顶角相等) ∠1=∠4(已知) = (对顶角相等) = ∴∠1= ∴∠1+ ∴∠ =∠2. ∴∠ +∠3=180° = ° 互补. 即∠1和∠3互补 和 互补
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对顶角、同位角、内错角与同旁内角
基础知识点:
1对顶角:(1)定义:有一个公共顶点,并且有一个角的两边分别是另一个角两边的反向延长线,具有这种位置关系的两个角,互为对顶角
(2
注意:
⑴对顶角是成对出现的,对顶角是具有特殊位置关系的两个角;
⑵如果∠α与∠β是对顶角,那么一定有∠α=∠β;反之如果∠α=∠β,那么∠α与∠β不一定是对顶角
1、如图,直线AB、CD相交于点O,OE平分∠BOC.已知∠BOE=65°,
求∠AOD、∠AOC的度数.
2、同位角、内错角与同旁内角
如图,直线b
a,被直线l所截
①∠1与∠5在截线l的同侧,同在被截直线b
a,的上方,叫做同位角(位置相同)
②∠5与∠3在截线l的两旁(交错),在被截直线b
a,之间(内),叫做内错角(位置在内且交错)
③∠5与∠4在截线l的同侧,在被截直线b
a,之间(内),叫做同旁内角。
④三线八角也可以成模型中看出。
同位角是“A”型;内错角是“Z”型;同旁内角是“U”型。
1、如图,∠1的内错角是,它们是直线、被直线所截得的;
∠1的同位角是,它们是直线、被直线所截得的;
∠1的同旁内角是,它们是直线、被直线所截得的;
2.如图,下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是…………………………………()
(A)①、②、③(
B)①、②、④(C)②、③、④(D)①、②、③、④
E
65
O
A
D
C
B
3、如图,图中的同位角共有…………………( ) (A )6对 (B )8对 (C )10对 (D )12对
二、巩固练习:
1.下面四个图形中,∠1与∠2是对顶角的图形的个数是( ) A .0 B .1 C .2 D .3
12
1
2
1
2
1
2
3.如图,直线AB 、CD 相交于点O ,OE ⊥AB ,O 为垂足,如果∠EOD = 38°,
则∠AOC = ,∠COB = 。
O
D E
C
B
A
2.三条直线两两相交于同一点时,对顶角有m 对,交于不同三点时,对顶角有n 对,则m 与n 的关系是
( )
A .m = n
B .m >n
C .m <n
D .m + n = 10
4.如图,直线AB 、CD 相交于点O ,∠1-∠2=64°,
则∠AOC=______.
5、如图,直线AB 、CD 相交于O ,OD 平分∠AOF ,OE ⊥CD 于点O , ∠1=50°,求∠COB 、∠BOF 的度数.。
