计算化学实例
高一化学计算题型总结归纳

高一化学计算题型总结归纳化学是一门基础科学,其中计算题型是学习和理解化学知识的重要一环。
本文将对高一化学计算题型进行总结归纳,并提供一些解题技巧和实例,以帮助同学们更好地应对化学计算题。
一、摩尔计算题摩尔计算是化学计算中最基础的一种题型,涉及到物质的摩尔质量、摩尔比、摩尔体积等。
解题时需要根据摩尔质量的计算公式M = m/n,其中M为摩尔质量,m为质量,n为物质的摩尔数。
以下是一个实例:实例1:计算化合物A(CH2)5OH的摩尔质量。
解析:根据摩尔质量的计算公式,需要计算该化合物中各元素的摩尔质量,并将其累加。
摩尔质量C = 12.01 g/mol,H = 1.008 g/mol,O = 16.00 g/mol。
化合物A(CH2)5OH的摩尔质量 = 12.01 × 1 + 1.008 × 6 + 16.00 × 1 =60.15 g/mol。
二、溶液计算题溶液计算是指根据溶液的体积、浓度等信息计算相关物质的质量、浓度或溶度的题型。
解题时需要掌握溶液中溶质和溶剂的摩尔关系以及浓度计算公式。
以下是一个实例:实例2:已知有100 mL浓度为0.1 mol/L的硝酸银溶液,求其中硝酸银的质量。
解析:根据浓度的计算公式c = n/V,其中c为浓度,n为溶质的摩尔数,V为溶液的体积。
硝酸银的摩尔质量为107.87 g/mol。
硝酸银的摩尔数n = c × V = 0.1 mol/L × 0.1 L = 0.01 mol。
硝酸银的质量 = n ×摩尔质量 = 0.01 mol × 107.87 g/mol = 1.08 g。
三、配位化学计算题配位化学计算题是指根据配位化合物的配位数、化学计量比等信息计算配位反应中的物质质量、摩尔比等题型。
解题时需要了解配位化合物中配体和中心离子的摩尔关系以及配位数等概念。
以下是一个实例:实例3:已知配位化合物[Fe(C2O4)3]3-的分子式为[Fe(C2O4)3(H2O)3],求其中含有的Fe2+离子的摩尔数。
化学习题范例气体的摩尔体积计算问题

化学习题范例气体的摩尔体积计算问题化学习题范例:气体的摩尔体积计算问题摩尔体积是化学中一个重要的概念,它指的是一摩尔气体所占据的体积。
在许多化学计算中,需要用到气体的摩尔体积来解决问题。
本文将以一些典型的化学习题为例,介绍气体摩尔体积的计算方法。
1. 摩尔体积的定义摩尔体积是指在一定的温度和压力下,1摩尔气体所占据的体积,通常用标准状况下的摩尔体积进行计算。
标准状况是指温度为273.15K (0℃)和压力为标准大气压下(1 atm,或约为101.3 kPa)。
2. 摩尔体积的计算公式根据理想气体状态方程PV = nRT,摩尔体积计算公式为V = (RT)/P,其中V为摩尔体积,R为气体常量(8.314 J/(mol·K)),T为温度(K),P为压力(Pa)。
3. 气体摩尔体积的计算实例3.1 问题一:求氢气的摩尔体积根据题目给出的条件,假设温度为25℃(即298K),压力为1 atm。
代入计算公式,可得V = (8.314 J/(mol·K) × 298K) / (1 atm × 101.3kPa/atm) ≈ 24.47 L/mol。
因此,氢气的摩尔体积约为24.47升/摩尔。
3.2 问题二:求氧气的摩尔体积假设温度为27℃(即300K),压力为1.5 atm。
根据计算公式,可得V = (8.314 J/(mol·K) × 300K) / (1.5 atm × 101.3 kPa/atm) ≈ 16.40 L/mol。
因此,氧气的摩尔体积约为16.40升/摩尔。
4. 摩尔体积与气体的物理特性摩尔体积与气体的物理特性密切相关。
不同气体在相同的温度和压力下,其摩尔体积可能不同。
根据理想气体状态方程,摩尔体积与气体分子的质量有关,分子质量越大,摩尔体积越大。
5. 摩尔体积的应用摩尔体积的计算在化学实验和工业生产中具有重要的应用价值。
化学反应中的酸碱滴定计算实例

化学反应中的酸碱滴定计算实例酸碱滴定是化学实验中常用的一种定量分析方法,它通过加入一种已知浓度溶液到另一种待测溶液中,以确定待测溶液中酸碱的浓度。
本文将介绍几个化学反应中的酸碱滴定计算实例。
实例一:酸碱滴定计算浓度假设有一种硫酸溶液(A)的浓度为0.1 mol/L,想知道其中含有多少硫酸。
首先,用一个滴定管取一定体积的A溶液,加入少量的酚酞指示剂,颜色变成粉红色。
然后,用另一个滴定管滴加氢氧化钠溶液(B)到A溶液中,当颜色由粉红色变为无色时,滴定停止。
滴定完成后记录滴定所需的氢氧化钠溶液B的体积为V mL。
根据酸碱滴定反应的化学方程式:H2SO4 + 2NaOH → Na2SO4 + 2H2O根据化学方程式的配比,可以得到摩尔比为1:2,即每1 mol的硫酸对应2 mol的氢氧化钠。
因此,滴定所需的氢氧化钠溶液B的摩尔数可以表示为:n = V × C(V为体积,C为氢氧化钠的浓度)。
假设滴定所需的氢氧化钠溶液B的摩尔数为n1 mol,则硫酸溶液A 中硫酸的摩尔数为2n1 mol。
由于硫酸溶液A的体积未知,所以无法直接计算出硫酸的质量。
实例二:酸碱滴定计算相对分子质量假设有一种含有未知酸的溶液,需要确定该酸的相对分子质量。
首先,用一个滴定管取一定体积的该溶液,加入酚酞指示剂,颜色变成粉红色。
然后,用氢氧化钠溶液滴定该酸溶液,当颜色由粉红色变为无色时,滴定停止。
滴定完成后记录滴定所需的氢氧化钠溶液的体积为V mL。
根据酸碱滴定反应的化学方程式:HnX + nNaOH → NaX + nH2O其中,HnX表示待测酸溶液,n为酸的酸度。
根据化学方程式的配比,可以得到摩尔比为1:1,即每1 mol的酸对应1 mol的氢氧化钠。
因此,滴定所需的氢氧化钠溶液的摩尔数可以表示为:n = V × C。
假设滴定所需的氢氧化钠溶液的摩尔数为n2 mol,则待测酸溶液中酸的摩尔数为n2 mol。
由于该酸的体积未知,所以无法直接计算出该酸的质量。
化学平衡常数的计算与应用实例

化学平衡常数的计算与应用实例化学平衡常数是化学反应达到平衡时,反应物与生成物浓度的比值的数学描述。
它对于分析化学、物质代谢、环境工程等领域具有重要意义。
本文将介绍化学平衡常数的计算方法,并提供一些应用实例说明其在实际中的应用。
一、化学平衡常数的计算方法化学平衡常数(K)的计算与化学反应的平衡式息息相关。
在一般情况下,如果有化学反应:aA + bB ⇌ cC + dD则该反应的平衡常数表达式为:K = ([C]^c[D]^d) / ([A]^a[B]^b)其中,[A]、[B]、[C]和[D]分别代表反应物A、B以及生成物C、D 的浓度。
上标a、b、c和d分别代表反应物和生成物的摩尔系数。
通过实验测定反应物和生成物的浓度,并代入上述表达式,即可计算出化学平衡常数K的值。
二、应用实例1. 气相反应的平衡常数计算考虑以下气相反应:2NO2(g) ⇌ N2O4(g)已知在240℃时,NO2和N2O4的初始浓度分别为0.2 mol/L和0.6 mol/L。
在平衡时,浓度分别为0.05 mol/L和0.75 mol/L。
根据上述平衡式,可以列写平衡常数表达式:K = ([N2O4]^1) / ([NO2]^2)代入实验数据,可以计算得到:K = (0.75^1) / (0.05^2) = 300因此,在240℃时,该反应的平衡常数K为300。
2. 溶液反应的平衡常数计算考虑以下溶液反应:Fe3+(aq) + SCN-(aq) ⇌ Fe(SCN)2+(aq)已知在某实验条件下,Fe3+、SCN-和Fe(SCN)2+的浓度分别为0.002 mol/L、0.003 mol/L和0.001 mol/L。
根据上述平衡式,可以列写平衡常数表达式:K = ([Fe(SCN)2+]^1) / ([Fe3+]^1[SCN-]^1)代入实验数据,可以计算得到:K = (0.001^1) / (0.002^1 * 0.003^1) ≈ 55.56因此,在该实验条件下,该反应的平衡常数K约为55.56。
初中化学化学方程式计算典例word文档
初中化学化学方程式计算典例word文档
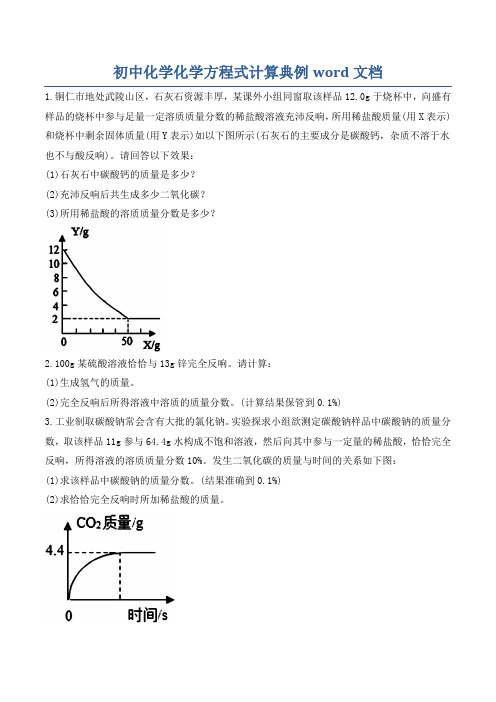
1.铜仁市地处武陵山区,石灰石资源丰厚,某课外小组同窗取该样品1
2.0g于烧杯中,向盛有样品的烧杯中参与足量一定溶质质量分数的稀盐酸溶液充沛反响,所用稀盐酸质量(用X表示)和烧杯中剩余固体质量(用Y表示)如以下图所示(石灰石的主要成分是碳酸钙,杂质不溶于水也不与酸反响)。
请回答以下效果:
(1)石灰石中碳酸钙的质量是多少?
(2)充沛反响后共生成多少二氧化碳?
(3)所用稀盐酸的溶质质量分数是多少?
2.100g某硫酸溶液恰恰与13g锌完全反响。
请计算:
(1)生成氢气的质量。
(2)完全反响后所得溶液中溶质的质量分数。
(计算结果保管到0.1%)
3.工业制取碳酸钠常会含有大批的氯化钠。
实验探求小组欲测定碳酸钠样品中碳酸钠的质量分数,取该样品11g参与6
4.4g水构成不饱和溶液,然后向其中参与一定量的稀盐酸,恰恰完全反响,所得溶液的溶质质量分数10%。
发生二氧化碳的质量与时间的关系如下图:
(1)求该样品中碳酸钠的质量分数。
(结果准确到0.1%)
(2)求恰恰完全反响时所加稀盐酸的质量。
4.将4g含有可溶性杂质的硫酸铜样品溶于足量水,再向所得溶液中逐滴参与75g一定溶质质量分数的氯化钡溶液(杂质不与氯化钡溶液反响)。
实验进程中,生成沉淀的质量与滴入氯化钡溶液的质量关系如下图。
试计算:
(1)恰恰完全反响时,生成沉淀质量是________g。
(2)样品中硫酸铜的质量分数是多少?
(3)反响后的溶液中,氯化钡的质量是多少?。
化学方程式计算例题

化学方程式计算例题概述化学方程式的计算是化学中重要的一部分。
通过计算化学方程式可以确定化学反应中的物质的量、质量、体积等相关信息,从而更好地理解化学反应的过程和结果。
本文将通过一些实例,介绍化学方程式的计算方法。
实例1:酸碱反应的计算题目:根据下列化学方程式,计算产物中氯化钠和硫酸铁(III)的物质的量。
化学方程式:2HCl + Fe2(SO4)3 → 2FeCl3 + 3H2SO4解答:根据化学方程式可知,1 mol的HCl和1 mol的Fe2(SO4)3反应可以生成2 mol的FeCl3和3 mol的H2SO4。
根据摩尔比例关系,我们可以根据已知条件计算出所需的物质的量。
已知条件: HCl的物质的量为0.5 mol根据化学方程式的摩尔比例关系,可以得到:Fe2(SO4)3的物质的量 = (2 mol FeCl3 / 2 mol HCl) * 0.5 mol HCl = 0.5 mol因此,氯化钠的物质的量为0.5 mol,硫酸铁(III)的物质的量为0.5 mol。
实例2:氧化反应的计算题目:根据下列化学方程式,计算产物中二氧化碳和水的质量。
化学方程式:2C2H2 + 5O2 → 4CO2 + 2H2O解答:根据化学方程式可知,2 mol的C2H2和5 mol的O2反应可以生成4 mol的CO2和2 mol的H2O。
根据摩尔比例关系,我们可以根据已知条件计算出所需的物质的质量。
已知条件: C2H2的质量为10 g首先,根据C2H2的相对分子质量可计算出C2H2的物质的量:C2H2的物质的量 = (10 g C2H2) / (26 g/mol C2H2) = 0.385 mol根据化学方程式的摩尔比例关系,可以得到:CO2的物质的量 = (4 mol CO2 / 2 mol C2H2) * 0.385 mol C2H2 = 0.77 molH2O的物质的量 = (2 mol H2O / 2 mol C2H2) * 0.385 mol C2H2 = 0.385 mol接下来,根据CO2和H2O的相对分子质量,可以计算出它们的质量:CO2的质量 = 44 g/mol * 0.77 mol = 33.88 g H2O的质量 = 18 g/mol * 0.385 mol = 6.93 g因此,二氧化碳的质量为33.88 g,水的质量为6.93 g。
教学案例:化学方程式的简单计算

化学方程式的简单计算在化学学科中,方程式是非常重要的概念,涉及到化学反应的基本过程。
化学方程式可以理解为化学反应过程的表达式,它表明了反应中各成分的摩尔比例和化学反应的程度。
化学方程式的表示有一定的规范,一般来说,它包括两部分:反应物和产物。
反应物通常写在左边,而产物则写在右边。
方程式中以箭头表示反应方向,箭头左侧表示反应物,箭头右侧表示产物。
然而,化学方程式的表达并不是简单的写出来,还需要进行一些简单计算。
以下是一些化学方程式的计算例子。
例1:氢气和氧气反应生成水的化学方程式是:H2 + O2 → H2O其中,H2和O2是反应物,H2O是产物。
根据方程式,可知一摩尔的H2和O2可以反应生成一摩尔的H2O。
问题: 20克的H2和20克的O2,可以反应生成多少克的H2O?解答:首先将质量转化为摩尔数。
根据元素的相对原子质量,可以计算出一摩尔的H2的质量为2g,一摩尔的O2的质量为32g。
因此,20克的H2相当于10摩尔,20克的O2相当于0.625摩尔。
根据化学方程式,可知一摩尔的H2可以生成一摩尔的H2O,因此10摩尔的H2可以生成10摩尔的H2O。
而一摩尔的O2可以生成一摩尔的H2O,因此0.625摩尔的O2可以生成0.625摩尔的H2O。
因此,总共可以生成10.625摩尔的H2O,相当于10.625 × (2+16) = 202.5克的H2O。
总结:在化学方程式的计算过程中,需要将质量转化为摩尔数,根据方程式中摩尔比例的关系,计算出反应物可以生成的产物的摩尔数,最后将摩尔数转化为质量即可。
例2:燃烧20克甲烷(CH4)需要多少克氧气(O2)才能完全燃烧?解答:首先可以写出甲烷燃烧的化学方程式:CH4 + 2O2 → CO2 + 2H2O其中,CH4是反应物,O2是反应物,CO2和H2O是产物。
根据化学方程式中的比例关系,一摩尔CH4需要两摩尔O2才能完全燃烧。
因此,20克的CH4相当于0.5摩尔。
化学能量与平衡常数计算实例

化学能量与平衡常数计算实例化学能量和平衡常数是化学反应中重要的概念。
化学能量指的是反应过程中释放或吸收的能量,而平衡常数则是描述反应的平衡状态的量。
本文将通过一些实例来说明如何计算化学能量和平衡常数。
实例一:燃烧反应的化学能量计算燃烧反应是一种常见的化学反应,其化学能量可以通过热量变化来计算。
以甲烷燃烧为例,化学方程式为:CH4 + 2O2 -> CO2 + 2H2O。
在这个反应中,甲烷和氧气是反应物,二氧化碳和水是生成物。
根据化学方程式,可以得知每1摩尔甲烷燃烧所释放的能量为-890.4千焦。
如果需要计算燃烧一定质量的甲烷所释放的能量,可以使用下面的公式:能量 = 质量 ×热值例如,燃烧10克甲烷所释放的能量为:能量 = 10克 × (-890.4千焦/摩尔) × (1摩尔/16.04克) = -554.5千焦这样,我们就可以通过计算化学能量来了解燃烧反应的能量变化。
实例二:平衡常数的计算平衡常数描述了反应在平衡状态下反应物和生成物的浓度之间的关系。
以一元一次反应为例,其平衡常数可以通过实验数据来计算。
假设我们有一个反应体系,反应方程式为:A -> B。
我们可以通过实验测定反应物A和生成物B的浓度来计算平衡常数。
首先,我们需要测定反应物A和生成物B的浓度。
假设在平衡状态下,反应物A的浓度为0.1 mol/L,生成物B的浓度为0.05 mol/L。
然后,我们可以使用下面的公式计算平衡常数:平衡常数 = [B] / [A]其中,[B]表示生成物B的浓度,[A]表示反应物A的浓度。
根据给定的浓度数据,可以得到平衡常数为:平衡常数 = 0.05 mol/L / 0.1 mol/L = 0.5这样,我们就可以通过实验数据计算出反应的平衡常数。
实例三:燃烧反应的平衡常数计算燃烧反应也可以通过平衡常数来描述。
以甲烷燃烧为例,其平衡常数可以通过燃烧热和标准生成焓来计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Wiberg键级: 4.1( Co-Co和Fe-Fe: 0.9-1.5)
4. 成键轨道分析
方法: AOMix软件 重要轨道的原子成份
重叠Mulliken键级
NBO成键分析
NBO轨道成份
分子轨道的原子轨道组合
NBO轨道成键图
LUMO
HOMO
确定第5个成键轨道!
4,2: 0.17
HOMO 4,3: 1.37
HOMO-1
4,4: 1.83
蓝移氢键的发现
形成正常氢键X-H...Y时, X-H键伸长, 其振 动频率红移, 因为氢键的形成导致X-H键减 弱 但是在某些体系中, 氢键形成却导致 X-H缩 短, 振动频率蓝移 它在1957年观测到时并未引起注意, 一直到 1988年重新被发现, 才引起对它本质的研究 这是一个定性问题, 在定性上与通常的看法 不同!!
(1)优化整个氢键聚合体 (2)从formcheck文件得到其总电子密度 (3)把优化结构中的除一个单体外的原子都变成ghost原子, 如 F-Bq, H-Bq, 计算单点能, 从得到的formcheck文件中生成单 体电子总密度 (4) 对其它单体实施上述方法 (5)用cubman程序, 从第(2)步得到的电子总密度中减去后面各 个单体的电子总密度, 得到电子差密度, (6) 用Gaussview画出电子差密度图
HOMO
HOMO-3
HOMO-1
HOMO-4
几何优化结构
角度的势能面扫描
CASSCF计算
(4,4): HOMO-1, HOMO: LUMO,LUMO+1 (6,6): HOMO-2, HOMO-2, HOMO: LUMO, LUMO+1,LUMO+2
LUMO+1
4,1: 0.64
LUMO
(1) 确定理论等级的影响
F3C-H...FH体系的氢键键长(A)与作用能量(Kcal/mol)
相关能 不是蓝 移的起 源!
基组的 影响不 大
(2)蓝移是否必须以C为中心
C 结论: 不需要必须 : 是C为中心
Si
N
P
(3)蓝移与受体上取代基
F3CH...HNRnH3-n中的取代效应: R(C-H)=1.0878
基态寻找
自旋多重度的寻找
– – – – 最低自旋多重度(S=1或2) 自旋较高的多重度(S=3或4) …… 直到找到能量最低的自旋多重度态!
对称性破损态
对称性破损态: 总自旋是配对的, 但是自旋α 和β的空间轨道不同, 比如双自由基态 对称性破损态都是相对于对称性限制而导 致的电子配对而言的, 方法: 把RHF强制改为UHF, 无对称性 (NOSYM), S=1, 计算其波函数, 用自旋密度 就可以看出电子在空间是否配对, 不配对就生成双自由基态
泛函和基组的影响
3-21G* BP86, BLYP, B3LYP, B3P86 结论: 基组和泛函不影响轨道的形状
3个未占据轨道: LUMO+2 LUMO+1 LUMO
8 个 占 据 轨 道
对波函数的成键分析
程序AOMix 对象: Ar’CrCrAr’, 及对比体系Ar’CoCoAr’, Ar’FeFeAr’ LUMO-HOMO能级差: 2.02eV,
计算化学及其应用
计算化学实例(二) An Instance Using Chemical Model
五重键化合物的合成
Synthesis of a Stable Compound with Fivefold Bonding Between Two Chromium(I) Centers 存在五重键的双Cr(I) 稳定化合物的合成 T. Nguyen, et al. Science, 310, 844(2005)
已有的结果
体系为: X-H...Y, 实验上:
– X为CF3或CCl3, – Y为苯, 二甲醚, 三甲酰甲烷, 环氧乙烯
理论研究: e suuuuuuuuuuu u 蓝移 F3 C H L Y e suuuuuuuuuu u 红移 H O HL Y
但是氢键电子重新分布对 于蓝移与红移没有什么差 别!
dxy轨道有一定的重叠, 不可忽略, 应该看成第5个键!!
HOMO
5.模型分子H3CCr-CrCH3
计算内容
几何优化 不同泛函 不同基组
电子结构(B3LYP/6-31G*)
LUMO HOMO-2
HOMO
HOMO-3
HOMO-1
HOMO-4
电子结构α态
(单重态双自由基, B3LYP/6-31G*) LUMO HOMO-2
单体的结构
Ar’
简化模型
最简模型
3. 电子结构的计算
闭壳层单点能计算以得到电子成键信息 实验结构, B3LYP/6-31G* 检验可靠性: 开壳层检验波函数的稳定性:E(S=3)>E(S=1) 对称性破损态检验(E(S=1, 破损态)<E(S=1)
– 自旋污染(spin contamination)很小(S2=0.036) – 单重态的双自由基是基态! – 但是双自由基态和限制DFT的轨道相同
结论: 与受体上取代基关系不大!
(4)电荷转移是蓝移起源吗?
自然键电 荷分析
转移的电荷少, 不是蓝移起源!
电子差密度图
0.47 +0.47
电子差密度图直观反 映了电子的重新分布
结论: HF对HCF3的 影响主要是静电作 F3CH...偶极矩 用, 电子重新分布 不是蓝移的起源
F3CH...HF
电子差密度图生成方法
计算化学及其应用
模型化学的实例 An Instance Using Model Chemistries
蓝移氢键的物理起源
On the Physical Origin of Blue-shift Hydrogen Bonds X. Li, L. Liu & H. B. Schlegel, J. Am. Chem. Soc., 124, 9639-9647 (2002) 目的: 用计算化学研究反常氢键的物理本质
红移
蓝移
结论
排斥导致键缩短, 吸引导致键伸长 蓝移: 排斥作用大, 缺少来自静电作用的吸引 红移: 排斥作用小, 不能抵消来自静电的吸引 二者的差别仅仅在于此消彼长。 纯粹静电作用, 轨道相互作用都不是蓝移氢键 的起源
氢键能量的计算
氢键键能, 比如(H2O)2
– E=E[(H2O)2] 2E(H2O) δE(BSSE)
但是在计算中, 基组误差相当大, (基组重叠 误差)
– 在 (H2O)2的计算中使用的基组是H2O的两倍
因此, E被高估了! 修正办法: 平衡法(counterpoise method)
– 几何结构为氢键聚合物的结构, 但是其余的单体 的各个原子用ghost原子代替
δ E ( BSSE ) = E XY ( X ) E X ( X ) + E XY (Y ) E Y (Y )
(5)轨道相互作用
电子转移和重新分布是LUMO 和HOMO混合的结果!
(6)静电作用
能 量
负电荷 作用
作用
正电荷
C-H 键 中 的 力
正, 负, , , 作用
偶极矩和多极矩作用
偶极矩作用, 类 似于负电荷作用
多极矩作用, 吸引作用, 力为负, 产生蓝移!!
(7)势能曲线
F3C-H...FH F2H-H...FH FO-H...FH
基本过程
1. 2. 3. 4. 实验结构及结论 计算模型的建立 方法的选择与验证 化学成键信息的分析
1. Cr-Cr化合物的实验结构
Cr(I)-Cr(I)键 短得反常 (1.835A)! Fe-Fe: 2.53 Co-Co: 2.80
基本原子轨道
成键图像
ቤተ መጻሕፍቲ ባይዱ
成键图像支 持五重键!
2. 从实验结构搭建模型
