二次曲线的射影与度量
本章是平面射影几何的精华.
a11 S (x1, x2 , x3 ) a12
a12 a22
a13 x1 a23 x2 0,
或
S
XAX' 0.
( A A', 秩( A) 1)
a13 a23 a33 x3
§ 5.1 二次曲线的射影定义
一、二次曲线的代数定义
定义4.1 坐标满足
定义4.1' 坐标满足
3
S aij xi x j 0 (aij a ji ) (4.1) i, j1
的所有直线[u1, u2, u3]的集合称 为一条二级曲线. 其中(bij)为三 阶实对称阵, 秩(bij)≧1.
注1. S, T 均为高等代数中的实三元二次型. 从代数上看, S=0,
T=0为相同的代数对象;从几何上看, 是同一几何对象的不同描述.
因此统称为二次曲线. 注2. 在需要时,S=0, T=0均可写为矩阵格式.
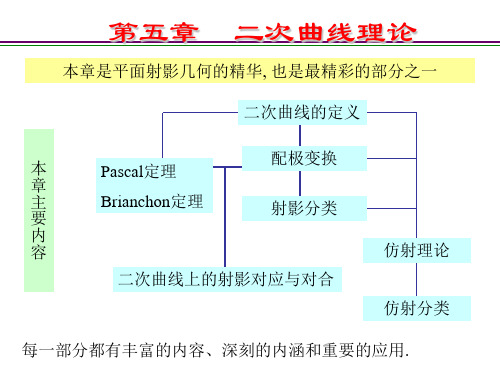
第五章 二次曲线理论
本章是平面射影几何的精华, 也是最精彩的部分之一 二次曲线的定义
本
Pascal定理
章
主
Brianchon定理
要
内
容
配极变换 射影分类
仿射理论
二次曲线上的射影对应与对合
仿射分类
每一部分都有丰富的内容、深刻的涵和重要的应用.
§ 5.1 二次曲线的射影定义
一、二次曲线的代数定义
定义4.1 坐标满足
§ 4.1 二次曲线的射影定义
二、二次曲线的几何结构
定理4.2 设二阶曲线Γ由射影线束O(P)与O'(P)生成. 则在Γ上任 意取定相异二点A,B, 与Γ上的动点M连线可得两个射影线束
A(M ) B(M ).
证明. 设Γ由O(P) O'(P)生成. A(M ) B(M )
二次曲线

二次曲线- 二次曲线二次曲线- 正文也称圆锥曲线或圆锥截线,是直圆锥面的两腔被一平面所截而得的曲线。
当截面不通过锥面的顶点时,曲线可能是圆、椭圆、双曲线、抛物线。
当截面通过锥面的顶点时,曲线退缩成一点、一直线或二相交直线。
在截面上的直角坐标系(x,y)之下,这些曲线的方程是x,y 的二元二次方程:。
若截面不通过锥面的顶点,令截面与锥面轴线所成的角为θ,锥面的半顶角为α,则当时,所截曲线为圆;当时,截面与锥面的所有母线都相交,所截曲线为椭圆;当θ=α时,截面与锥面的一条母线平行,所截曲线为抛物线;当0≤θ<α时,截面与锥面的两条母线平行,所截曲线为双曲线。
焦点与准线如果圆锥曲线不是圆,则在圆锥曲线所在的平面上存在一定点和一定直线,使得圆锥曲线上任何一点到该定点和定直线的距离之比为常数,这个定点称为圆锥曲线的焦点,定直线称为圆锥曲线的准线。
为了得到焦点与准线,只需作一个球面内切于圆锥面并同时与圆锥曲线所在的平面σ相切。
设球面与平面σ相切于点F,球面与圆锥面相切于一个圆,这个圆所在的平面为ω,ω与σ相交于直线l,则点F,就是焦点,直线l就是准线(图1)。
二次曲线二次曲线这时,圆锥曲线上任意一点P到焦点F的距离|PF|与到准线l的距离|PD|之比为:。
其中θ,α都与P在曲线上的位置无关,所以是常数。
这个常数称为圆锥曲线的离心率,记为e。
当截线是椭圆时,e<1;当截线是双曲线时,e>1;当截线是抛物线时,e=1。
对于椭圆或双曲线,存在两个合于以上要求的球面,因此椭圆或双曲线都有两个焦点与两条准线。
每个焦点与其相应的准线都有上述性质。
抛物线只有一个焦点与一条准线。
若椭圆的两个焦点为F1,F2。
如图2所示的球面与圆锥面相切的圆为C1,C2。
这时对于椭圆上任意一点P,令通过P的母线OP(O为圆锥面的顶点)与C1、C2的交点分别为A、B。
则P 到F1的距离|PF1|与P到F2的距离|PF2|之和为|PF1||PF2|=|P A||PB|=|AB|。
高等几何(第六章)

0 0
二阶曲线 秩为2
(实、虚、平行、相交、普通直 线、无穷远直线等5种情况)
秩为1
一对重合的普通直线:x12
0
一对重合的无穷远直线:x32 0
5 11
§4 二次曲线的度量性质
➢我们在引入了复元素的仿射平面上讨 论二次曲线的度量性质。
➢在讨论二次曲线的仿射性质时,仿射 不变图形无穷远直线起了至关重要的作 用,那么正交变换下保持不变的元素除 了无穷远直线外还有什么?
➢为什么要讨论圆点呢? ➢定理4.2 正交变换保持圆点不变。
x'
y'
x x
cos sin
y y
sin cos
a13 a23
或
x' y'
x cos -x sin -
y y
sin cos
a13 a23
前者I(1,i,0),J(1,-i,0)保持不变, 后者I(1,i,0),J(1,-i,0)分别变为J,I.
➢定理2.1 双曲线、椭圆各有唯一的中 心,且为普通点,抛物线的中心为无穷 远点。
二次曲线的中心坐标:
A11 A12
A21 A22
A31 0 A31 A32 0 A32
A13 A23 A33 1 A33
➢例1. 判定二次曲线:x12-2x1x2+x222x1x3+x2x3-x32=0的类型,并求出它的 中心。
直径与共轭直径的关系是相互的。
一直径的方向与该直径的共轭直径的方向(该直 径的极点的方向)称为一对共轭方向。注意抛物线 的情形。
例:过一直径两端点的切线平行于该直径的共轭 直径。
P
✓过一直径两端点的切线的交点为该直径 的极点即为一个无穷远点。
二次曲线的射影理论

第五章 二次曲线的射影理论本章首先给出射影平面上二次曲线的射影定义,然后在此基础上讨论二次曲线的射影性质及其分类。
§1 二次曲线的射影定义1.1 二次曲线的射影定义定义1.1 在射影平面上,若齐次坐标(x 1,x 2,x 3)满足下列三元二次齐次方程)(031,ji ij j i j i ij a a x x a ==∑=其中a ij (i ,j=1,2,3)为实数,并且至少有一个不是零,则这些点的集合称为二阶曲线。
二阶曲线的方程可以写成矩阵形式:()0321333231232221131211321=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛x x x a a a a a a a a a x x x其中(a ij )用A 表示叫系数矩阵,用| A |或| a ij |表示系数行列式。
定理1.1 两个不同中心的射影对应线束对应直线的交点构成一条二阶曲线。
证明在射影平面上建立射影坐标系后,设两个线束的方程为α+λβ=0,α′+λ′β′=0,由于它们是射影对应,所以λ,λ′满足:a λλ′+b λ+c λ′+d=0 (ad -bc≠0).由以上三个式子消去λ,λ′得,0)()()()(=+''--''d c b a βαβαβαβα即0='-'-'+'βαβαββααc b d a .因为α,β,α′,β′都是 x 1,x 2,x 3的一次齐次式,所以上式是关于x 1,x 2,x 3的二次齐次方程,它表示一条二阶曲线。
而且α=0与β=0的交点和α′=0与β′=0的交点的坐标都满足这个方程,因此形成此二阶曲线的两个线束中心也在这条二阶曲线上。
定理1.1的逆定理也成立,定理 1.1 中形成二阶曲线的两个射影对应线束的中心并不具有特殊性,可以证明,二阶曲线上任意两点都可以看作生成这条二阶曲线的射影对应线束的中心。
定理1.2 设有一条二阶曲线,它是由两个成射影对应的线束对应直线的交点构成的,那么以这条二阶曲线上任意两点为中心向曲线上的点投射直线,则可以得到两个成射影对应的两个线束。
二次曲线的射影理论

第五章 二次曲线的射影理论本章首先给出射影平面上二次曲线的射影定义,然后在此基础上讨论二次曲线的射影性质及其分类。
§1 二次曲线的射影定义1.1 二次曲线的射影定义定义1.1 在射影平面上,若齐次坐标(x 1,x 2,x 3)满足下列三元二次齐次方程)(031,ji ij j i j i ij a a x x a ==∑=其中a ij (i ,j=1,2,3)为实数,并且至少有一个不是零,则这些点的集合称为二阶曲线。
二阶曲线的方程可以写成矩阵形式:()0321333231232221131211321=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛x x x a a a a a a a a a x x x其中(a ij )用A 表示叫系数矩阵,用| A |或| a ij |表示系数行列式。
定理1.1 两个不同中心的射影对应线束对应直线的交点构成一条二阶曲线。
证明在射影平面上建立射影坐标系后,设两个线束的方程为α+λβ=0,α′+λ′β′=0,由于它们是射影对应,所以λ,λ′满足:a λλ′+b λ+c λ′+d=0 (ad -bc≠0).由以上三个式子消去λ,λ′得,0)()()()(=+''--''d c b a βαβαβαβα即0='-'-'+'βαβαββααc b d a .因为α,β,α′,β′都是 x 1,x 2,x 3的一次齐次式,所以上式是关于x 1,x 2,x 3的二次齐次方程,它表示一条二阶曲线。
而且α=0与β=0的交点和α′=0与β′=0的交点的坐标都满足这个方程,因此形成此二阶曲线的两个线束中心也在这条二阶曲线上。
定理1.1的逆定理也成立,定理 1.1 中形成二阶曲线的两个射影对应线束的中心并不具有特殊性,可以证明,二阶曲线上任意两点都可以看作生成这条二阶曲线的射影对应线束的中心。
定理1.2 设有一条二阶曲线,它是由两个成射影对应的线束对应直线的交点构成的,那么以这条二阶曲线上任意两点为中心向曲线上的点投射直线,则可以得到两个成射影对应的两个线束。
第四章 二次曲线理论-第五节 二次点列上的射影变换课件ppt课件

§ 4.5 二次点列上的射影变换
三、二次点列上的对合
例2. (P.135, Ex. 4) 证明. 二阶曲线上对合的几何条件与点列上对合的形式完全相 同, 照抄P.77, §2.5, 例2.14. 例3. (P.135, Ex. 5)
证明. 如图, 过P0另作的弦P1Q1, 设 AP1, AQ1分别交'于P1', Q1'. 由定理4.24, 在上(P, P1, …)(Q, Q1, …)为对合(以P0为对合 中心). 于是, 在A为束心的线束中, A(P, P1, …)A(Q, Q1, …)为对合. 从而, 在'上, 对应(P', P1', …)(Q', Q1', …)为对合. 由上述对合可知, 其对应点的连线P'Q', P1'Q1'必定共点于对合 中心.
§ 4.5 二次点列上的射影变换
一、二次点列上的射影对应
2、二次点列上四点的交比
定义4.13 设A, B, C, D为二次点列上四点. 则其交比定义为 (AB, CD)=S(AB, CD).
其中S为上任意一点. 若上述交比为–1, 则称这四点构成二次点 列上一个调和点组. 注:由推论4.3, (AB,CD)与S的选取无关, 本定义合理.
§ 4.5 二次点列上的射影变换
一、二次点列上的射影对应
S(P) S'(P') S(P)
S'(P') 与一维射影对应的桥梁
(P)
'(P')
(P)
'(P')
交比、调和比、Steiner作图法、透视轴……
二、二次点列上的射影变换
射影轴、不变元素、分类、与Pascal定理的关系……
高等几何(第五章)
第五章 二次曲线的射影理论
➢ 这一章将用射影的观点研究二次曲线。 ➢ 首先介绍二次曲线的射影定义; ➢ 然后研究二次曲线的射影性质; ➢ 最后给出二次曲线的射影分类。
§1 二次曲线的射影定义
1.1 二次曲线的射影定义
➢我们既可以用点几何的观点讨论二次曲线 又可以用线几何的观点来讨论,但是我们主 要用点几何的观点讨论问题。
,
q3)
p1 p2
p3
已知点Q(q1,q2,q3)在直线p上:(q1,
q2
p3
, q3)
p1 p2
0.
p3
配极原则:若点Q在直线p上,则点Q的极线通过直线p 的极点。
A
O
K
P 在两个不同中心的射影对应
B’ S
A’ K’
M
O’
线束O(P)、O’ (P) 所构成的二
B 阶曲线上任取两点A、B,由这
两点向二阶曲线投射直线,得 到两个线束A(M)、B(M).
✓ 须证明A(M) 与B(M) 射影对应,已知 O(M) 与O’ (M)
射影对应: O(A, B, P, M )O'( A, B, P, M )
➢直观上,二阶曲线的切线的集合为二级曲 线,二级曲线切点的集合为二阶曲线,且这 二阶曲线、二级曲线表示同一条二次曲线。
➢定理1.3 一条非退化的二阶曲线的切线的 集合是一条非退化的二级曲线;反之,一条 非退化的二级曲线的切点的集合是一条非退 化的二阶曲线。
设S≡∑aijxixj=(x1x2x3)A(x1x2x3)T是一条非退化的二阶曲 线,[u1,u2,u3]是该二阶曲线的任意一条切线,现在寻找 u1,u2,u3满足的方程。
➢定义3.2 定点P关于一条二阶曲线的 调和共轭点的轨迹是一条直线,这条直 线叫做点P关于此二阶曲线的极线,点P 叫这条直线关于此二阶曲线的极点。
第七章二次曲线的射影性质
注1 验证两点P, Q关于共轭, 只要验证上式.
注2 P在上, 则Spp=0, 规定:上的点关于自共轭.
§ 7.3 配极变换
2. 极点与极线
共轭点轨迹p
P 定义7.7 对于点P, 若 P
则称P关于的
切线p
为P关于的极线, 方程为Sp=0. 反之, 称P为直线p关于 的极点.
§ 7.3 配极变换
0, i 1, 2,3.
§ 7.3 配极变换
二、配极变换
1. 配极变换 非异实对 注4 称矩阵类 非退化 二阶曲线 配极变换
定义7.9 称由
ui aij x j
j 1 3
i 1,2,3, aij a ji , | aij | 0.
(4.18)
决定的同底点场与线场之间的变换为关于非退化二阶曲线 : S=0的配极变换. 注1 (4.18) 即 u1 a11 x1 a12 x2 a13 x3 | aij | 0, 0 (4.18) u2 a12 x1 a22 x2 a23 x3 u a x a x a x 13 1 23 2 33 3 3 表示点x与直线u是关于 : S=0的极点极线关系. 注2 任一非退化二阶曲线都决定了平面上的一个配极变换.
§ 7.5 二次曲线的仿射理论
利用中心坐标, 可直接写出的直径方程为
a11 x1 a12 x2 bx3 0(b为常数 ) 即 a11 y x b. a12
第五六章二阶曲线射影理论复习资料
第五章 二阶曲线射影理论复习一、基本概念1. 二阶曲线代数定义:射影坐标为),,(321x x x 的满足方程)(031,ji ij j i j i ija a x x a==∑=的点的集合称为二阶曲线,其中ij a 为实数且至少有一个不为0。
几何定义:在射影平面上成射影对应的两个线束的对应直线的交点的集合称为二阶曲线。
2. 二级曲线代数定义:射影坐标为),,(321u u u 的满足方程)(031,ji ij j i jiijb b uu b ==∑=的直线的集合称为二级曲线,其中ij b 为实数且至少有一个不为0。
几何定义:在射影平面上成射影对应的两个点列的对应点的连线的集合称为二级曲线。
3. 极点与极线共轭点:给定二阶曲线c 及不在c 上的点P ,过P 作直线交c 与M 、N ,点Q 满足(MN ,PQ )=–1,则称点P 与Q 关于二阶曲线c 调和共轭,或点Q 与P 关于c 互为共轭点。
极点与极线:点P 关于二阶曲线c 的共轭点的轨迹称为P 关于c 的极线;而点 P 称为此直线的极点。
规定:对于二阶曲线上的点的极线为该点的切线。
二、重要定理1. 平面上无三点共线的五点唯一确定一条(非退化)二阶曲线。
2. 从二阶曲线上任一点向其上四定点连直线,则所得四线的交比是常数。
3. 从二阶曲线上任两点向其上动点连直线,则所得两个线束是射影线束。
4. 巴斯卡定理:二阶曲线的内接简单六点形的对边交点共线(此线称为巴斯卡线)。
布利安桑定理:二级曲线的外切简单六线形的对顶点连线共点(此点称为布利安桑点)。
例1 试证明若两个三点形同时内接于一条二阶曲线,则它们必同时外切于另一条二阶曲线。
证明:如图所示,考察二阶曲线的内接六点形C B A ABC ''', 根据巴斯加定理知A C A C Z CB BC Y B A AB X '⨯'=''⨯=''⨯=,, 三点共线。
在第四章与二次曲线的射影定义中的演示文稿共32页文档
A B 0 A'' B' 0 a'b c'd 0
消去, ', 得到交点P的坐标
所满足的齐次方程为
§ 5.1 二次曲线的射影定义
二、二次曲线的几何结构
: aAA'dBB'bAB'cA' B 0
(4.2)
显然, 这是关于(x1,x2,x3)的二次齐次方程, 为一个二阶曲线, 且两个 束心O, O'的坐标满足(1.1). 定理证毕.
l1 : A a1x1 a2 x2 a3x3 0; l2 : B b1x1 b2 x2 b3x3 0.
则O(p)可以表示为A+B=0. 同理O'(p')可以表为A'+'B'=0.
设两个射影线束的对应式为
a'b c'd 0
(ad bc 0)
设则对应直线的交点为P(x1,x2,x3), 则P的坐标满足
§ 5.1 二次曲线的射影定义
二、二次曲线的几何结构
定理1.1 不同心的两个射影线束的对应直线交点的全体构成一 条经过此二线束束心的二阶曲线.
注 对偶地, 有定理4.1'. 证明 设O(p), O'(p')为平面上两个射影线束, 并取定射影坐标系. 在O(p)中取定相异两直线l1: A=0, l2: B=0, 即
3
T bijuiu j 0 (bij bji ) (4.1') i, j1
的所有直线[u1, u2, u3]的集合称 为一条二级曲线. 其中(bij)为三 阶实对称阵, 秩(bij)≧1.
注1. S, T 均为高等代数中的实三元二次型. 从代数上看, S=0,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
r lto swih t ep oe tv r p ry ea in t h rj ciep o e t .
Ke r s rj cin ma n t d ;p lrl e h r ncC nu ae yWo d :p oe t ; g i e oa i ; a mo i O j g t o u n
在 以 度 量 为不 变量 的几 何 中 . 用 切 线 和 割 线 对 于 特 殊 利 的 二次 曲 线 圆 . 度 量 的 角 度 描 述 了 它 们 之 间 的 独特 性 质 与 从 关 系 。而 对 于 一般 的 二 次 曲 线 , 这 些 性 质 射 影 化 . 而 更 将 从
进 一 步 认 识 它 们之 间的 内在 联 系 。
mo e wi e y lh ap rma n y i t o c s t e ma niu e pr p r y ofqu d i u v nd isi na e r d l . ' e p e i l n du e g t d o e t a rcc r ea t n t r h
射 影 性 质 的 内在 联 系 。 关 键 词 : 影 ; 量 ; 线 ; 和 共 轭 射 度 极 调
中图分类号 : 8 文献标 识码 : 文 章编号 :6 2—3 9 2 0 ) 4 0 0 O O1 2 A 17 4 X( 0 8 O — 0 7一 2
P o t n a d M a nt d f o i rjci n g i eo nc e o u C
ME G igj n N Ln -a g i
( pa t e fM a he a isT a gs a ac r le e. Ta gs a 6 00, De rm nto t m tc n h n Te he s C lg o n h n 0 30 Chi ) na
而在 圆 0 中 又有
一
r= l 2
l z
故 由 ( ) 第二 式 . 2的 得
l 1 I  ̄『 『 l 确 . . : - P z
M N) ~ 1 并 设 = e 则 由调 和共 轭 的 性 质 , 一 . . 得 圈 I 一 点 关 于 二 次 曲线 的 极 线 的确 定 在 图 l中 . , 为 圆 0 外 一点 , 为 圆 ( 半径 。P 设 ’ r )的 S和 1 、 圆 ( 切线 . , " 为 I )的 s 丁为 切 点 。P 同 时 又表 示 以点 P 为 中 心 的 线束 . 一动直 线 P ∈P. 线 P与 圆 交 于 M . 两 点 。设 直 N ; 动 直 线 P上 的单 位 矢 量 . 为 直线 P上 的 一动 点 . 令 为 X 且
mo i C n u a in ee n s nc O j g to lme t ,wec n d tr n h ea in e we n p lrp ita d p lr l e a ee mie t e r lt s b t e oa on n o a i o n
维普资讯
第 2 l卷 第 4期 20 0 8年 0 7月
唐 山 学院 学报
J u n l fTa g h n C l g o r a n s a o l e o e
Vo . 1 NO 4 I2 .
J 12 0 u. 0 8二 次 曲线 的 射 影 与 度 量
Ab ta t n a niu e ge sr c :I m g t d om e r ty, t e a i o a tt t r i e b he o d t n e i he r l ton f qu n iy de e m n d y t r un a g nt s u e n t e e a a rc c v n t ho og a i o e r s d i he g n r lqu d i ur e i p t r ph cge m ty. U sn he r lto e w e n ha — he i g t ea i nsb t e r
I ̄l 2 - 一r=常数。 P
I 一e — I { 硪 - Si =,
将 :z 代 入 上 式 . 且 两 边 平 方 . 并 得
( ) 的几 何 意 义 是 当直 线 p在线 束 P 中 转 动 时 . 4式
的值 是 固定 的 . 此 点 Y 属 于 一 条 与 垂 直 的 直 线 . 因 且
z 一2 . ) - 一r=o z G 6 x+r  ̄ 2
设 A .。为 方 程 ( ) A 1 的两 个 根 . 则有
() 1
A= I 。
由根 与 系数 的 关 系 , 知
A +A 一 2 ;・ 。 (
『。 雨 『 . =i A
) A A = . 。 一r 2 () 2
孟 令 江
( 山 师 范学 院 数 学 与 信 息 科 学 系 . 北 唐 山 03 0 ) 唐 河 60 0
摘要 : 度量 几何 中圆的切 割线之 间所确 定 的数 量关 系, 广 到射 影几 何 里一 般 二次 曲线 中, 推 利用调
和 共轭元 素之 间的关系 。 更广泛 地确定 了极 与极 线的相 互关 系, 着重介 绍 了二次 曲线的度量性 质与
=
() 3
在直 线 p 上 确 定 M . P 的 第 四 调 和 点 Y. ( . N. 即 PY
cPy. N = M
一
= 一t
由此 可 解 得 =
将其与() 2 式结 合 . 得
- p - p・
一 —
;・ S = - ) P
() 4
・
当 落 在 圆周 上时 . 有
