黄安基第2章平面力系的简化和平衡
合集下载
第二章_平面力系的简化和平衡

13P YA 6
F
y
0
YA YB P 2P 0
a M A 2aP 2 P(2a ) 3aYB 0 3 5P 25Pa MA YB 6 6
建筑力学
二、静定与超静定问题
对所研究的系统,如果对系统中的所有物体列出的 独立平衡方程数等于未知量的数目,那么总可以求 出待求未知量,这样的问题称为静定问题。如果对 系统中的所有物体列出的独立平衡方程数目小于未 知量总的数目,那么仅仅通过静力平衡无法求解, 这样的问题称为超静定问题. 静力学只能解决静定问题。
建筑力学
静定悬臂梁 静定拱架
静定简支梁
超静定拱
超静定连续梁
建筑力学
§2-6
平面静定桁架
由一些细长 直杆按适当方式 分别在两端连接 而成的几何形状 不变的结构
桁架
建筑力学
一、桁架简化计算的假设 1.各杆件都用光滑铰链相连接 2.各杆件轴线都是直线,并通过铰链中心 3.所有外力(荷载及支座反力)都作用在节点上
M Mi 0
结论:
平面力偶系平衡的解析条件(充要):该力偶 系的力偶矩的和为零.
建筑力学
§2-4
平面任意力系
风力
重力 浮力 阻力
建筑力学
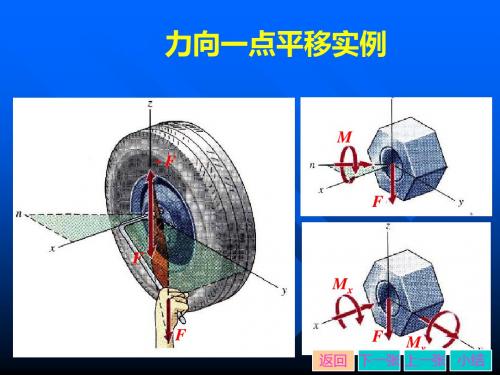
一 、力线平移定理
o
F
M Mo F
F
A o F
o
M F
A
F
A
F ' F F
FR Fxi i Fyi j 0
M M o ( Fi ) 0
F1
F2
F3
建筑力学
F
y
0
YA YB P 2P 0
a M A 2aP 2 P(2a ) 3aYB 0 3 5P 25Pa MA YB 6 6
建筑力学
二、静定与超静定问题
对所研究的系统,如果对系统中的所有物体列出的 独立平衡方程数等于未知量的数目,那么总可以求 出待求未知量,这样的问题称为静定问题。如果对 系统中的所有物体列出的独立平衡方程数目小于未 知量总的数目,那么仅仅通过静力平衡无法求解, 这样的问题称为超静定问题. 静力学只能解决静定问题。
建筑力学
静定悬臂梁 静定拱架
静定简支梁
超静定拱
超静定连续梁
建筑力学
§2-6
平面静定桁架
由一些细长 直杆按适当方式 分别在两端连接 而成的几何形状 不变的结构
桁架
建筑力学
一、桁架简化计算的假设 1.各杆件都用光滑铰链相连接 2.各杆件轴线都是直线,并通过铰链中心 3.所有外力(荷载及支座反力)都作用在节点上
M Mi 0
结论:
平面力偶系平衡的解析条件(充要):该力偶 系的力偶矩的和为零.
建筑力学
§2-4
平面任意力系
风力
重力 浮力 阻力
建筑力学
一 、力线平移定理
o
F
M Mo F
F
A o F
o
M F
A
F
A
F ' F F
FR Fxi i Fyi j 0
M M o ( Fi ) 0
F1
F2
F3
建筑力学
平面力系的简化和平衡
(1)取梁AB为研究对象 (2)画受力图 (3)选取投影坐标轴和矩心。
(4)列平衡方程求解。 X 0, XA P1Cos450 0 Y 0,YA P1Sin450 P2 RB 0 mA(F) 0,P1Sin450 2P2 5m RB 7 0
XA 424N RB 207N YA 317N
X 0, XA 0
Y 0,YA Q P 0
mA
(F)
0,
mA
Q
l 2
3P
0
XA 0,YA 190KN,mA 435KNm
校核:
m B ( F ) m A 3 Y A 1 . 5 Q 4 3 3 1 1 5 . 5 9 9 0 0
矢量 和。
tga
| Y | X
| |
•主矩:原力系中所有各 力系对简化中心O的力矩 的代数和。
MM 0 M 0(F ) 0
返回 下一张 上一张 小结
2.2.3 平面一般力系的平衡条件、平衡方程式
1.基本形式:
X 0 Y 0
M OF 0
X 0
2.二力矩形式: MA(F) 0 MB(F) 0
S33.7 1 K,S N 23.4K,S N 12.8 9 KN
•
计算结果正值与假设方向相同,负值与假设方向相反。
返回 下一张 上一张 小结
2.2.4 平面特殊力系
1.平面汇交力系 X0
Y 0
2.平面力偶系: mi 0
3.平面平行力系 or
X 0
MOF 0
M AF 0 M BF 0
X0,S3C4 o05 sS2C4 o05 sP 2S3 in 00 0
(4)列平衡方程求解。 X 0, XA P1Cos450 0 Y 0,YA P1Sin450 P2 RB 0 mA(F) 0,P1Sin450 2P2 5m RB 7 0
XA 424N RB 207N YA 317N
X 0, XA 0
Y 0,YA Q P 0
mA
(F)
0,
mA
Q
l 2
3P
0
XA 0,YA 190KN,mA 435KNm
校核:
m B ( F ) m A 3 Y A 1 . 5 Q 4 3 3 1 1 5 . 5 9 9 0 0
矢量 和。
tga
| Y | X
| |
•主矩:原力系中所有各 力系对简化中心O的力矩 的代数和。
MM 0 M 0(F ) 0
返回 下一张 上一张 小结
2.2.3 平面一般力系的平衡条件、平衡方程式
1.基本形式:
X 0 Y 0
M OF 0
X 0
2.二力矩形式: MA(F) 0 MB(F) 0
S33.7 1 K,S N 23.4K,S N 12.8 9 KN
•
计算结果正值与假设方向相同,负值与假设方向相反。
返回 下一张 上一张 小结
2.2.4 平面特殊力系
1.平面汇交力系 X0
Y 0
2.平面力偶系: mi 0
3.平面平行力系 or
X 0
MOF 0
M AF 0 M BF 0
X0,S3C4 o05 sS2C4 o05 sP 2S3 in 00 0
第2章 平面力系的简化与平衡

F
i 1
n
yi
(2-9)
FR
平面汇交力系平衡的必要与充分条件是平面汇交力系的 合力为零。由式(2-9)得
FR = FRx + FRy =
2 2
( Fxi ) + ( Fyi ) 2 = 0
2 i 1 i 1
n
n
ቤተ መጻሕፍቲ ባይዱ
;
从而得平面汇交力系平衡方程
F
i 1
n
xi
0
F ;
i 1
合成的理论依据是力的平行四边形法则或三角形法则。 设作用在刚体上汇交于O点的力系F1、F2、F3和F4,如图2.2(a) 所示,求其合力。首先将F1和 F2两个力进行合成,将这两个力矢 量的大小利用长度比例尺转换成长度单位,依原力矢量方向将两力 矢量进行首尾相连,得一折线abc,再由折线起点向折线终点作有 向线段ac,即将折线abc封闭,得合力 F12,有向线段ac的大小 为合力的大小,指向为合力的方向,同理,力F12与F3的合力为 F123 ,依次得力系的合力FR,如图2.2(b)所示,可以省略中间求 合力的过程,将力矢量F1、F2、F3和F4依次首尾相连,得折线 abcde,由折线起点向折线终点作有向线段ae,封闭边ae表示其 力系合力的大小和方向,且合力的作用线汇交于O点,多边形 abcde称为力的多边形,此法称为力的多边形法则。作图时力的 顺序可以是任意的,力的多边形的形状会发生变化,但并不影响合 力的大小和方向,如图2.2(c)所示。
2. 平面力偶的性质与力偶的等效定理 平面力偶的性质是力偶没有合力,因此不能与 一个力等效;力偶只能与一个力偶等效;力偶 矩与矩心点位置无关。 平面力偶的等效定理:在同一平面内两个力偶 等效的必要与充分条件是两个力偶矩相等。
第二章 平面力系的简化与平衡

问题。
在物体系统平衡问题的研究中,一般是对符合可解条件的分 离体先行求解,然后将求得的力通过作用与反作用的关系,转移 到其他物体上作为已知力,逐步扩大已知力的数目,最终使所有 的未知量全部求解。这是求解物系平衡问题的大致顺序。
上式只有一个方程式,可解一个未知量。
第三节
物体系统的平衡
一、静定与静不定问题的概念
工程中常会遇到由若干物体通过一定的约束组成的系统。当整个
系统平衡时,则组成该系统的每个物体均是平衡的。假设系统由n个 物体组成,且每一个物体都受平面一般力系作用。则该系统就可列出 3n个独立的平衡方程,从而求解出3n个未知量。因此,对于所研究的 平衡问题,其未知量的个数少于或等于可列出的独立平衡方程的数目 时,全部未知量都可由静力平衡方程求出,这样的问题称为静定问题。 例如,图2-12a、b所示的结构均为静定问题。反之,如果未知量的个
1) 主矢FR′≠0,主矩MO≠0:力系简化为一个合力FR。由力的平移
定理的逆过程(见图2-4)可知,其主矢FR′与主矩MO可进一步合成为 一个合力FR,合力的大小FR= FR′,合力作用线到简化中心的距离 为
至于合力作用线在O点的哪一侧,则应根据主矢的方向与主矩的转 向确定。
2) 主矢FR′=0,主矩MO≠0:力系简化为一个力偶M。因为主矢为零, 所以原力系不论向哪一点简化均与一个力偶等效。由于力偶对作用面 内任一点之矩恒等于力偶矩,故合力偶矩即等于主矩,且与简化中心 的位置无关。 3) 主矢FR′≠0,主矩MO=0:力系简化为作用于简化中心的一个力 FR。因为主矩为零,所以原力系与作用于简化中心的主矢等效,且
式中,α 为主矢FR′的作用线与x轴之间所夹锐角,其具体指 向由∑Fx与∑Fy的正负确定。 应用力偶的合成法则可以将附加平面力偶系合成为一个合力偶,其 合力偶矩等于力偶系中各分力偶矩的代数和,即
平面力系的简化与平衡方程.ppt

§4.4 平面平行力系的平衡方程
平面平行力系:各力的作用线在同一平面内且相互平行的力系叫∼。 设有F1, F2 … Fn 各平行力系, 向O点简化得:
主矢R R'F O
主矩M O mO (Fi )Fi xi
合力作用线的位置为:
xR
MO R'
Fi xi F
平衡的充要条件为 主矢 R =0
QPW N A NB 0
解得:
N A 210 kN, NB 870 kN
§4.5 物体系统的平衡
一、静定与静不定问题的概念
我们学过:
平面汇交力系 X 0 Y 0
两个独立方程,只能求两个独立 未知数。
力偶系 mi 0 一个独立方程,只能求一个独立未知数。
平面
X 0
i1
由于简化中心是任意选取的,故此式有普遍意义。
即:平面任意力系的合力对作用面内任一点之矩等于力系
中各力对于同一点之矩的代数和。
§4.3 平面一般力系的平衡条件与平衡方程
由于 R =0 为力平衡
MO=0 为力偶也平衡
所以平面任意力系平衡的充要条件为:
力系的主矢 R 和主矩 MO 都等于零,即:
的原图上)
解除约束
由 mA (Fi )
0
P2a N B
3a0,
N B
2P 3
X 0 XA 0
Y 0 YB NB P0,
YA
P 3
§4.3 平面一般力系的平衡条件与平衡方程
[例] 已知:P=20kN, m=16kN·m, q=20kN/m, a=0.8m
求:A、B的支反力。
YD 6 YG' 1 0
第2章 力系的简化与平衡

解: 取微元如图
q x q l
三角形 的面积
P
l
0
x l
q
dx
1 2
ql
由合力矩定理 得 h 2l
3
Ph
l
q dx x
0
l
0
x2 l
q dx
3.平面力偶系的合成
已知: M1, M 2 , M n ;
n
M
M
i 1
i
Mi
已知: M1, M 2 , M n ;
任选一段距离d
M1 d
F1
M2 d
F2
M1 F1d
M 2 F2d
Mn d
Fn
M n Fnd
=
=
FR F1 F2 Fn
FR F1 F2 Fn
=
M
M n
i 1
i
Mi
=
=
M FRd F1d F2d Fnd M1 M 2 M n
例2-3
已知:图示平面共点力系; 求:此力系的合力. 解:用解析法
r j)
Fy
FR '
r
MO MO (F) 3F1 1.5P1 3.9P2 2355kN m
(2)求合力及其作用线位置:
x
d
3.514m
cos 900 70.840
(3)求合力作用线方程:
r
MO MO FR x FRy y FRx x FR'y y FR'x
2. 作用线的位置:
A
T1 C
F1 F1´
AC F2 (内分反比关系)
CB F1
F2´
AC CB AB F2 F1 R
理论力学02平面力系的简化和平衡
主矢R ' F1 F2 F3 Fi 主矩 M O m1 m2 m3
mO ( F1 ) mO ( F2 ) mO ( Fi )
2 2 R ' R ' R ' ( X ) ( Y ) 大小: x y 2 2
主矢 R
雨搭
车刀
固定端(插入端)约束
说明
①认为Fi这群力在同一
平面内;
② 将Fi向A点简化得一 力和一力偶;
③RA方向不定可用正交
分力YA, XA表示; ④ YA, XA, MA为固定端 约束反力; ⑤ YA, XA限制物体平动,
MA为限制转动。
简化模型
=
=
≠
=
3
由于
平面一般力系的平衡条件与平衡方程
为力平衡 MO=0 为力偶也平衡
力F 力偶(F,F )
说明: ①力线平移定理揭示了力与力偶的关系:力 力+力偶
(例பைடு நூலகம்丝锥)
②力平移的条件是附加一个力偶m,
且m与d有关,m=F•d
③力线平移定理是力系简化的理论基础。
2 平面力系向指定点的简化
向一点简化 一般力系(任意力系) 汇交力系+力偶系 (未知力系) (已知力系) 汇交力系 力 , R'(主矢) , (作用在简化中心) 力偶系 力偶 ,MO (主矩) , (作用在该平面上)
i 1 i 1
n
n
与前式比较,:
M o ( F R ) FRY x A FRX y A
M o ( FR ) M o ( Fi )
i 1 n
即
合力对任意点之矩,等于其各个分力对同一点之矩的代数和
第二章平面力系的简化和平衡
31
主矢R ' F1 F2 F3 Fi
主矩 MO m1 m2 m3
mO (F1)mO (F2 )mO (Fi )
大小:R' R'x2 R'y2 ( X )2 (Y )2
主矢 R 方向:
(移动效应)
tg1
Ry Rx
t g1
Y X
简化中心 (与简化中心位置无关) [因主矢等于各力的矢量和]
的合力为零。 即:
R 0 Rx2 Ry2 0
Rx X 0 Ry Y 0
为平衡的充要条件,也叫平衡方程 14
例2.2 求图示作用在O点之共点力系的合力。
解:取坐标如图。
合力在坐标轴上的投影为:
Rx=X=-400+250cos45-200×4/5 =-383.2 N
Ry=Y=250sin45-500+200×3/5 =-203.2N
力+力偶
(偶断丝连)
②力平移的条件是附加一个力偶m,且m与d有关,m=F•d
③力线平移定理是力系简化的理论基础。
30
2. 平面一般力系向一点的简化
一般力系(任意力系)向一点简化汇交力系+力偶系
(未知力系)
(已知力系)
汇交力系
力 , R'(主矢) , (作用在简化中心)
力偶系
力偶 ,MO (主矩) , (作用在该平面上)
21
平面力偶系:作用在物体同一平面的许多力偶叫平面力偶系 设有两个力偶
d
d
m1 F1d1;
m2 F2d2
又m1 P1d
m2 P2d
RA P1 P2' RB P1' P2
合力矩 M RAd (P1 P2' )d P1d P2'd m1 m2
第二章平面力系的简化与平衡
如打乒乓球,若球拍对球作用的力其作用线通过球心 (球的质心),则球将平动而不旋转;但若力的作用线与 球相切——“削球”,则球将产生平动和转动。 c
F
c
c
m
F
(a)
水土学院理论力学课程组
F
(b)
理论力学电子教程
第二章 平面基本力系 平面力系的简化与平衡
§2-2 平面汇交力系的合成与平衡
一、几何法 1、合成 应用力多边形法则,合力即为力多边形的封闭边。如图 所示。用解析式表达为
【解】 AB梁上作用有二个力偶组成的平面力偶系,在 A、 B 处的约束反力也必须组成一个同平面的力偶。作 AB 梁的受力图,如图(b)所示。
M1
M
M1
2
M
2
B B A
A
4m
60。
FA
FB
d
(a )
水土学院理论力学课程组
(b)
理论力学电子教程
第二章 平面基本力系 平面力系的简化与平衡
例2-5
M1
水土学院理论力学课程组
M
i
0
利用这个平衡条件,可以求解一个未知量。
理论力学电子教程
第二章 平面基本力系 平面力系的简化与平衡
例2-5
长为 4 m 的简支梁的两端 A、B 处作用有二 个力偶其力偶矩分别为 M 1 16 N m ,M 2 4 N m 。 求 A、B支座的约束反力。
1、是非题 (1)平面汇交力系平衡的充分与必要几何条件是:力多边 形自行封闭。( ) )
(2)力在某一固定平面上的投影是一个代数量。( (3)两个力
F1、 F 2
大小相等,则它们在同一轴上的投 )
影也相等。(
F
c
c
m
F
(a)
水土学院理论力学课程组
F
(b)
理论力学电子教程
第二章 平面基本力系 平面力系的简化与平衡
§2-2 平面汇交力系的合成与平衡
一、几何法 1、合成 应用力多边形法则,合力即为力多边形的封闭边。如图 所示。用解析式表达为
【解】 AB梁上作用有二个力偶组成的平面力偶系,在 A、 B 处的约束反力也必须组成一个同平面的力偶。作 AB 梁的受力图,如图(b)所示。
M1
M
M1
2
M
2
B B A
A
4m
60。
FA
FB
d
(a )
水土学院理论力学课程组
(b)
理论力学电子教程
第二章 平面基本力系 平面力系的简化与平衡
例2-5
M1
水土学院理论力学课程组
M
i
0
利用这个平衡条件,可以求解一个未知量。
理论力学电子教程
第二章 平面基本力系 平面力系的简化与平衡
例2-5
长为 4 m 的简支梁的两端 A、B 处作用有二 个力偶其力偶矩分别为 M 1 16 N m ,M 2 4 N m 。 求 A、B支座的约束反力。
1、是非题 (1)平面汇交力系平衡的充分与必要几何条件是:力多边 形自行封闭。( ) )
(2)力在某一固定平面上的投影是一个代数量。( (3)两个力
F1、 F 2
大小相等,则它们在同一轴上的投 )
影也相等。(
力系的简化和平衡
空间汇交力系可合成一合力F'R:
z MO O x F'R y
FR Fi Fi
力系中各力的矢量和称为空间力系的 主矢。主矢与简化中心的位置无关。
空间力偶系可合成为一合力偶, 其矩矢MO:
MO MO (Fi )
力系中各力对简化中心之矩矢的矢量和称为力系对简化 中心的主矩。主矩与简化中心的位置有关。
3.1.2 (空间任意)力系向一点的简化 结论: 空间力系向任一点O简化, 可得一力和一 力偶, 这个力的大小和方向等于该力系的主矢, 作用线通过简化中心O; 这个力偶的矩矢等于该 力系对简化中心的主矩。
空间任意力系向一点简化的结果可能出现四种情况: (1) F'R=0, MO≠0 ; (2) F'R ≠ 0, MO = 0 ; (3) F'R ≠ 0, MO≠0 ;
′ Fn
O Mn
3.1.2 (平面任意)力系向一点简化 平面一般力系中各力的矢量和称为平面一般力 系的主矢。主矢与简化中心的位置无关。
FR FRx + FRy Fx i Fy j
FR ( Fx ) 2 ( Fy ) 2
Fx cos( FR , i ) FR Fy cos( FR , j ) FR
A
m
B q C
FAy
FB
求得的FAx和FAy为负, 说明与图中 假设方向相反。
例: 求图示刚架的约束反力。
P
A
解: 以刚架为研究对象, 受力如图。
a
q b
Fx 0 : FAx qb 0
Fy 0 : FAy P 0
M A (F ) 0 :
1 2 M A Pa qb 0 2
z MO O x F'R y
FR Fi Fi
力系中各力的矢量和称为空间力系的 主矢。主矢与简化中心的位置无关。
空间力偶系可合成为一合力偶, 其矩矢MO:
MO MO (Fi )
力系中各力对简化中心之矩矢的矢量和称为力系对简化 中心的主矩。主矩与简化中心的位置有关。
3.1.2 (空间任意)力系向一点的简化 结论: 空间力系向任一点O简化, 可得一力和一 力偶, 这个力的大小和方向等于该力系的主矢, 作用线通过简化中心O; 这个力偶的矩矢等于该 力系对简化中心的主矩。
空间任意力系向一点简化的结果可能出现四种情况: (1) F'R=0, MO≠0 ; (2) F'R ≠ 0, MO = 0 ; (3) F'R ≠ 0, MO≠0 ;
′ Fn
O Mn
3.1.2 (平面任意)力系向一点简化 平面一般力系中各力的矢量和称为平面一般力 系的主矢。主矢与简化中心的位置无关。
FR FRx + FRy Fx i Fy j
FR ( Fx ) 2 ( Fy ) 2
Fx cos( FR , i ) FR Fy cos( FR , j ) FR
A
m
B q C
FAy
FB
求得的FAx和FAy为负, 说明与图中 假设方向相反。
例: 求图示刚架的约束反力。
P
A
解: 以刚架为研究对象, 受力如图。
a
q b
Fx 0 : FAx qb 0
Fy 0 : FAy P 0
M A (F ) 0 :
1 2 M A Pa qb 0 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
思考题
试指出图示平面汇交力系所作的力多边形各力 矢量关系如何?合成结果是什么?
(a)
(b)
(c)
(d)
理论பைடு நூலகம்学电子教程
第二章 平面力系的简化和平衡
水平梁AB中点C作用着力F,其大小等于20kN,方向与梁的轴线 成60º角,支承情况如图a 所示,试求固定铰链支座A和活动铰链支座B的约束 力。梁的自重不计。
【解】 先计算合力FR在x、y轴上的投影,有
故合力FR 的大小为 F F 2 F 2 2.02kN R Rx Ry
450
F2 F1
600
F3
其方向余弦则为 x
a
cosa FRx FR 0.164, cosb FRy FR 0.986
即
F4
a 80.340
FR
理论力学电子教程
o
F2
F1
Fn
理论力学电子教程
第二章 平面力系的简化和平衡
§2-1 平面汇交力系合成与平衡
一、合成
应用由力三角形法则推广得到的力多边形法则,合 力即为力多边形的封闭边。 P34
用解析式表达为
FR F1 F2 F3
FR F1 F2 ... Fn Fi F
n
如下图所示。 O
F
o
图 2-2 (b)
3、互成平衡的二力对同一点之矩的代数和为零。
F2
O
F1
图 2-2 (c)
理论力学电子教程
第二章 平面力系的简化和平衡
三、 合力矩定理 P39 表达式: M (F ) M (F ) O O R 证明:MO (F ) F d F r sin(a ) F r (sin a cos sin cosa ) F sin a r cos F cosa r sin x Fy y Fx MO (Fy ) MO (Fx ) M O ( F )
F3
F2
B
F1
F2
o
x
F1
o
a
b d c
理论力学电子教程
第二章 平面力系的简化和平衡
五、合成
当应用合力投影定理求出力系的合力在直角坐标系下的 投影Fx、Fy后,可用下式求出合力的大小和方向
FR Fx Fy ( Fx) 2 ( Fy ) 2
2 2
Fx cosa FR
( Fx ) 2 ( Fy ) 2
F· d 来度量力的转动效应。
l
A
F
d O 图2-1 B
(1)用扳手拧螺母; (2)开门,关门。
理论力学电子教程
第二章 平面力系的简化和平衡
该乘积根据力使物体的转动效应的不同,取适当的正负号称为 力F对点O之矩,简称力矩,以符号 M O (F ) 表示。 即 MO (F ) F d O点称为力矩的中心,简称矩心; O点到力F 作用线的垂直距离d,称为力臂。
0 分析铰B有: F 0 , F F cos 45 0 x1 2 BC
C
B
900
FBC 2F2
(1)
45
0
300
F2
F1
600
A
3 F1 2
D
(2)
0 F 0 , F F cos 30 0 分析铰C有: x CB 1
FCB
F2 6 ( 1 )、( 2 ) 0.612 F1 4
O
b
A
B
a FR
Fx
b
x
a
图a 力在坐标轴上的投影
理论力学电子教程
第二章 平面力系的简化和平衡
而如将力FR沿垂直的x、y坐标轴方向分解(图a),则所得 分力FRx、FRy的大小与力F在相应轴上的投影Fx、Fy的绝对值相等。 应注意 (1)力的投影是代数量,而力的分量是矢量;
y
b1 a1 O
(2)力投影无所谓作用点,而分力必须作用在 原力的作用点。 若已知FR在直角坐标轴上的投影为Fx和Fy,则 由几何关系可求出力FR的大小和方向,即 B
FA cos300 F cos600 FB sin 300 0 Fy 0,
a
a
FA sin 300 F sin 600 FB cos300 0 图a FA = F cos30=17.3 kN y1 FB = F sin30=10 kN
y
x1
F
思考:可否向其它轴,如(x1、y1)投影?
l
A
F
d B 力矩的正负号:力使物体绕逆时针方向 转动为正,反之为负。 O 图2-1 力矩的单位: 国际制 N· m,kN· m 工程制 公斤力· 米(kgf· m) 力矩的大小还可视为三角形OAB 的面积的两倍。 P39 应注意:在平面问题中,力对点之矩只取决于力矩的大小及其旋
转方向(力矩的正负),因此它是一个代数量。
第二章 平面力系的简化和平衡
20120917 水平梁AB中点C作用着力F,其大小等于20kN,方向与梁的轴线 例2-1 成60º角,支承情况如图 a 所示,试求固定铰链支座A和活动铰链支座B的约束
力。梁的自重不计。
解:1. 取梁AB作为研究对象。 2. 画出受力图。 Fx 0, A
F
B C
30º
理论力学电子教程
第二章 平面力系的简化和平衡
20120912第二章 平面力系的简 化和平衡 §2-1 平面汇交力系合成与平衡
§2-2 平面力偶系的合成与平衡 §2-3 平面任意力系的简化与平衡
理论力学电子教程
第二章 平面力系的简化和平衡
网上作业系统 1、告知作业网站的网址:222.18.54.19\homework。 2、告知学生用户的初始密码都是:123。 3、开学三周之内改选过教学班的学生,需要同时利用作业系统的 “选课”功能更改一下选课,使作业系统中的选课与教务处网站上的 选课结果相同。 4、开学后才选课的学生,可先通过作业系统提交一份登录申请,并 等候教师审批。
Fy F 1y F 2 y F ny
F
y
F1x ab, F 2 x bc, F 3x cd, Fx ad
因 ad ab bc cd ,故 y
F
A
D
同理可得 Fy F1y F 2 y F 3 y
F3
C
Fx F1x F 2 x F 3x
理论力学电子教程
第二章 平面力系的简化和平衡
力对物体作用时可以产生移动和转动两种效应。 力的移动效应取决于力的大小和方向; 为了度量力的转动效应,需引入力矩的概念。
理论力学电子教程
第二章 平面力系的简化和平衡
§2-2 力面力偶系的合成与平衡
一、力对点之矩
由下图及生活常识知,力F 使物体绕O点(某轴)转动的效应,不仅与力 的大小,而且与转轴(平面上O点)到力的作用线的垂直距离d有关,故用乘积
例2-2 用解析法求下图所示汇交力系的合力的大小和方向已 知 F1 1.5kN, F2 0.5kN, F3 0.25kN, F4 1kN
FRy Fiy 1.5 0 0.25 sin 600 1 sin 450 1.99kN
y
FRx Fix 0 0.5 0.25 cos600 1 cos450 0.332kN
x
60º
FA
FB
30º
可否向(x、x1)投影?结论? P36、61
理论力学电子教程
第二章 平面力系的简化和平衡
例2-4 如图所示结构ABCD,杆重及摩擦均可不计;在铰链B上作 用着力 F2 ,在铰链C上作用着力 F1 ,方向如图。试求当机构在图
示位置平衡时 F1 和 F2 两力大小之间的关系。 P69 【解】 首先可判断出BC是二力杆,作B铰、C铰的受力图
理论力学电子教程
第二章 平面力系的简化和平衡
2、力偶矩 P42 其转动效应——力对点之矩,即用力偶中的两个力对 其作用面内任一点之矩的代数和来度量。
M ( F , F ) F d 或 M F d 例如: M ( F ) M ( F )
O O
F x F ( d x) F d 力偶对作用面内任意一点之矩与矩心位置无关 P42
理论力学电子教程
第二章 平面力系的简化和平衡
平面力系包括平面基本力系和平面任意力系,平面基本力 系包括平面汇交力系和平面力偶系,它是研究复杂力系的基础。 平面汇交力系的定义: 各力的作用线在同一平面且相交于一点的力系。如图所示。 本章研究的两个问题: 平面汇交力系的合成与平衡问题。 研究方法: 几何法和解析法。
理论力学电子教程
第二章 平面力系的简化和平衡
四、力偶和力偶矩 1、力偶的概念 P41 把大小相等、方向相反、作用线平行的两个力 叫做力偶。并记作 ( F , F ) 。可用图2-4表示: 例如:丝锥、改锥(刀)、水龙头、方向盘等
F
d
力偶臂
F1
A
C D 图2-4
F
B
F
力偶作用面 图 2-3
F
F1
三、 力在坐标轴上的投影 由图a知,若已知力FR 的大小FR 和 y 其与x轴、y轴的夹角为a、b,则 Fx FR cosa Fy FR cos b FR sin a b 即力在某个轴上的投影等于力的大小 1 Fy 乘以力与该轴的正向间夹角的余弦。 a1 当a、b为锐角时,Fx、Fy均为正值; 当a、b为钝角时,Fx、Fy为负值。 注意力在坐标轴上的投影是代数量 。
i 1
F1 F2
a
F1 FR
b
F2
c
F3
d
F3
理论力学电子教程
