等量代换代求面积和差不变原理练习题
等量代换代求面积和差不变原理练习题

等量代换代求面积和差不变原理练习题
1.左以下图中,等腰直角三角形ABC的腰为10厘米,以C为圆心、CF为半径画弧线EF,组成扇形CEF。
假如图中甲、乙两局部的面积相等,那么扇形所在的圆的面积是多少?
3.左以下图中,扇形ABD的半径是4厘米,甲比乙的面积大3.44厘米2。
求直角梯形ABCD的面积。
(π=3.14)
4.在右上图的三角形中,D,E分别是所在边的中点,求四边形ADFE的面积。
5.下页左上图中,矩形ABCD的边AB为4厘米,BC为6厘米,三角形ABF比三角形EDF的面积大9厘米2,求ED的长。
6.右上图中,CA=AB=4厘米,三角形ABE比三角形CDE的面积大2厘米2,求CD的长。
影局部的面积和。
用割补法求面积练习题
1.求以下各图中阴影局部的面积:
(1)(2)
2.以等腰直角三角形的两条直角边为直径画两个半圆弧(见以下图),直角边长4厘米,求图中阴影局部的面积。
3.在左以下图所示的等腰直角三角形中,剪去一个三角形后,剩下的局部是一个直角梯形(阴影局部)。
已知梯形的面积为36厘米2,上底为3厘米,求下底和高。
4.在右上图中,长方形AEFD的面积是18厘米2,BE长3厘米,求CD的长。
5.以下图是甲、乙两个正方形,甲的边长比乙的边长长3厘米,甲的面积比乙的面积大45厘米2。
求甲、乙的面积之和。
6.求以下图(单位:厘米)中四边形ABCD的面积。
小学数学 等积变换求面积 PPT+课后作业 带答案

例题对角1线
对角线
对角线
如图所示,两个相等的等腰直角三角形与一个正方形摆放成梯形ABCD。已知等腰直角三 角形的斜边AB长度是8厘米,求梯形ABCD的面积。
斜边
斜边
斜边
大等腰三角形面积=斜边×斜边÷2 小等腰三角形面积=斜边×斜边÷2÷2 等腰直角三角形面积=斜边长度的平方÷4
练习1
如图所示,等腰直角三角形ABD和BCD拼成了一个直角梯形ABCD。已知BD长6厘米,求 梯形ABCD的面积。
G
B
A
连接DF,AC//DF
F
S ACF = S ACD = S 正方形ABCD ÷2
=10×10÷2
=50(平方厘米)
C
D
E
例题5
如图所示,四边形ABCD是一个直角梯形,以上底AD为边向外作长方形ADEF,面积为10 平方厘米,连接BE交AD于O,连接OC。求图中阴影部分的面积。
FE // AC // BC 和 FB // ED
6
等高三角形模型可得, S ABD = S ACD
所以三角形ABC的面积是三角形BDO面积的4倍
三角形ABC的面积=6×4=24(平方厘米)
例题3
如图所示,图中两个正方形的边长分别是6厘米和4厘米,则图中阴影部分三角形的面积是 多少平方厘米?
A
D 4
G
F
4
B
C
E
三角形面积=底×高÷2 阴影部分三角形的底是小正方形的一条边 而高也是小正方形的一条边 阴影部分的面积=4×4÷2=8(平方厘米)
在梯形中寻找面积 相等的三角形
AD // BC △ ABC和△DBC △ BAD和△CAD △ ABO和△CDO 连接BE
小学数学五年级奥数每天一题--等量代换求面积

小学数学五年级奥数每天一题:等量代换求面积
例1两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,求阴影部分的面积。
分析与解:阴影部分是一个高为3厘米的直角梯形,然而它的上底与下底都不知道,因而不能直接求出它的面积。
因为三角形ABC与三角形DEF完全相同,都减去三角形DOC后,根据差不变性质,差应相等,即阴影部分与直角梯形OEFC面积相等,所以求阴影部分的面积就转化为求直角梯形OEFC的面积。
直角梯形OEFC的上底为10-3=7(厘米),面积为
(7+10)×2÷2=17(平方厘米)。
所以,阴影部分的面积是17平方厘米。
例2在右图中,平行四边形ABCD的边BC长10厘米,直角三角形ECB的直角边EC长8厘米。
已知阴影部分的总面积比三角形EFG的面积大10平方厘米,求平行四边形ABCD的面积。
分析与解:因为阴影部分比三角形EFG的面积大10厘米2,都加上梯形FGCB后,根据差不变性质,所得的两个新图形的面积差不变,即平行四边行ABCD比直角三角形ECB的面积大10平方厘米,所以平行四边形ABCD的面积等于
10×8÷2+10=50(平方厘米)。
三年级下等量代换练习题

三年级下等量代换练习题1. 已知三角形ABC中,AB = 5 cm,AC = 7 cm,BC = 9 cm。
找出三角形DEF,使得DE = 2 cm,EF = 3 cm,DF = 4 cm。
2. 小明有一条长12 cm的木杆,他想将其分成两段,使得第一段比第二段长3 cm,应该如何切割?3. 假设一个矩形的长和宽分别为3 cm和8 cm,现在将其等量代换,使得长和宽都增加了5 cm,求新矩形的周长和面积。
4. 有一个长方体,长、宽和高的比例为2∶3∶4,其中长为6 cm,求其体积。
5. 如果一个长方形的周长是40 cm,长是宽的3倍,求长方形的面积。
1. 解答:根据三角形ABC的已知边长,我们可以通过等量代换的方法得到三角形DEF的边长。
设三角形DEF的边为DE = 2 cm,EF =3 cm,DF =4 cm。
根据等量代换的原理,我们可以得出:DE/AB = EF/AC = DF/BC2/5 = 3/7 = 4/9解方程得到:DE = 2/5 * AB = 2/5 * 5 = 2 cmEF = 3/7 * AC = 3/7 * 7 = 3 cmDF = 4/9 * BC = 4/9 * 9 = 4 cm所以,三角形DEF的边长为DE = 2 cm,EF = 3 cm,DF = 4 cm。
2. 解答:设第一段木杆的长度为x cm,则第二段的长度为x - 3 cm。
根据题目条件,得到方程:x + x - 3 = 12解方程得到:2x = 15x = 7.5所以,第一段木杆的长度为7.5 cm,第二段为7.5 - 3 = 4.5 cm。
3. 解答:原矩形的长为3 cm,宽为8 cm,所以原矩形的周长为(3 + 8) * 2 = 22 cm,面积为3 * 8 = 24 cm²。
等量代换后,矩形的长和宽增加了5 cm,新矩形的长为8 + 5 = 13 cm,宽为3 + 5 = 8 cm。
新矩形的周长为(13 + 8) * 2 = 42 cm,面积为13 * 8 = 104 cm²。
等量代换练习题

等量代换练习题等量代换是数学中的一个重要概念,它在解题过程中起到了至关重要的作用。
通过等量代换,我们可以将复杂的问题转化为简单的形式,从而更好地解决它们。
在本文中,我将为大家提供一些关于等量代换的练习题,并逐一解答,希望能够帮助大家更好地理解和运用等量代换。
练习题一:已知方程2x + 3 = 7,求解x的值。
解答:我们可以通过等量代换将这个方程转化为更简单的形式。
首先,我们将方程中的常数项3移到等号的右边,得到2x = 7 - 3。
接下来,我们将方程中的系数2移到等号的右边,得到x = (7 - 3) / 2。
最后,计算出x的值,即x = 4 / 2 = 2。
所以方程的解为x = 2。
练习题二:已知方程3(x + 2) = 2(x + 5),求解x的值。
解答:这个方程看起来比较复杂,但通过等量代换,我们可以将它转化为更简单的形式。
首先,我们将方程中的括号展开,得到3x + 6 = 2x + 10。
接下来,我们将方程中的常数项6移到等号的右边,得到3x = 2x + 4。
然后,我们将方程中的系数3移到等号的右边,得到x = 2x + 4。
最后,我们将方程中的系数2移到等号的左边,得到x - 2x = 4。
计算出x的值,即-2x = 4,所以x = -2。
所以方程的解为x = -2。
练习题三:已知方程2(x - 3) + 5 = 3(x + 1),求解x的值。
解答:这个方程看起来稍微复杂一些,但我们仍然可以通过等量代换将它转化为简单的形式。
首先,我们将方程中的括号展开,得到2x - 6 + 5 = 3x + 3。
接下来,我们将方程中的常数项-6 + 5移到等号的右边,得到2x - 1 = 3x + 3。
然后,我们将方程中的系数2移到等号的右边,得到-1 = 3x - 2x + 3。
最后,我们将方程中的系数3移到等号的左边,得到-1 - 3 = x。
计算出x的值,即x = -4。
所以方程的解为x = -4。
(完整)求面积(超多题)

=48-(S1+S2+S3)=18(平方厘米)
【题目】正方形ABCD边长4厘米,E、F分别是BC、AD的中点,P是中方形任意一点,求阴影部分的面积。
【解析】
如下图,
△APF面积×4=矩形MNDA面积,
△PEC面积×4=矩形MBCN面积,
(△APE面积+△PEC面积)×4=正方形ABCD面积=16(平方厘米)
【题目】一块长方形耕地,它由四个小长方形拼合而成,其中三个小长方形的面积分别为15、18、30公顷,图中阴影部分的面积是多少?
【解析】
因为阴影部分也是一长方形,所以只要求出它的长、宽是多少就行,为此设它的长、宽分别为a、b,面积为18公顷的长方形的长、宽分别为c、d.
按公式便有:
a×c=15,c×d=18,b×d=30,
因为三角形ABE、ADF是直角三角形,面积都是18平方厘米。而根据面积公式有
18=1/2×AB×BE,18=1/2×AD×DE,
AB=6厘米,AD=9厘米,即得两个简易方程:1/2×6×BE=18,1/2×9×DF=18,
BE=6厘米,DF=4厘米。
EC=BC-BE=9-6=3(厘米)
CF=CD-DF=6-4=2(厘米)
因为三角形BDC与CDE共顶点D,且CE=2BC,所以三角形CDE面积=2×三角形BDC面积=2×1=2
所以,三角形DEF面积=1+2+2+6+6+1=18。
【题目】平行四边形的面积是48平方厘米,E、F分别是BC、CD的中点,求阴影部分面积。
【解析】
如下图,
S1=48÷2÷2=12(平方厘米)
S2=48÷2÷2=12(平方厘米)
小学奥数 几何 割补法求面积、等差法 知识点+例题+练习 (分类全面)

巩固.在直角三角形ABC中,四边形DECF为正方形,若AD=7,DB=8,则ΔADE与ΔBDF的面积之和是多少?AD EB CF巩固、如图所示,用一张斜边长为29厘米的红色直角三角形纸片、一张斜边长为50厘米的蓝色直角三角形纸片、一张黄色的正方形纸片,拼成一个直角三角形.红、蓝两张三角形纸片面积之和是多少?例2、五边形的三条边的长和四个角的度数,如下图所示,那么它的面积是多少?巩固.求下图(单位:厘米)中四边形ABCD的面积。
例3、如左下图所示,在一个等腰直角三角形中,削去一个三角形后,剩下一个上底长5厘米、下底长9厘米的等腰梯形(阴影部分)。
求这个梯形的面积。
巩固.在左下图所示的等腰直角三角形中,剪去一个三角形后,剩下的部分是一个直角梯形(阴影部分)。
已知梯形的面积为24平方厘米,上底为4厘米,求下底和高。
例4、在一个等边三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几?巩固、如图,三个正方形的边长分别为8厘米、10厘米、6厘米拼在一起,求阴影部分的面积?巩固、下图是两块长方形草地,长方形的长是16,宽是10.中间有两条道路,一条是长方形,一条是平行四边形,那么有草部分的面积(阴影部分)分别有多大?等差法解题关键:找出组合图形的公共部分解题技巧:利用差不变原理进行等量代换:例1、如图ABCG是的长方形,AB=7,AG=4,DEFG是的长方形,GF=2,FE=10。
那么,三角形BCM的面积与三角形DEM面积之差是多少?巩固、如图ABCG是的长方形,AB=5,AG=3,DEFG是的长方形,GF=1,FE=9。
那么,三角形BCM的面积与三角形DEM面积之差是多少?例2、如图所示,平行四边形ABCD的边长BC长为8,直角三角形BCE的直角边CE长为6。
已知两块阴影部分的面积和比三角形EFG的面积大8,求CF的长度?巩固、如图,四边形BCEF是平行四边形,三角形ACB是直角三角形,BC的长是8厘米,AC长是7厘米。
30道小升初数学几何问题(附答案)
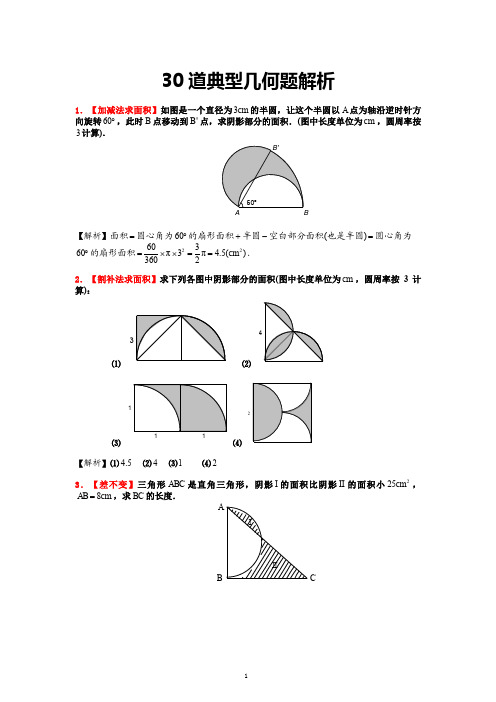
图1
图2
【解析】我们可以让静止的瓷砖动起来,把对角线上的黑瓷砖,通过平移这种动态的
处理,移到两条边上(如图 2).在这一转化过程中瓷砖的位置发生了变化,但数量没
有变,此时白色瓷砖组成一个正方形.大正方形的边长上能放 (1011) 2 51(块),白
色 瓷 砖 组 成 的 正 方 形 的 边 长 上 能 放 : 511 50 ( 块 ) , 所 以 白 色 瓷 砖 共 用 了 :
60 的扇形面积 60 π 32 3 π 4.5(cm2 ) .
360
2
2.【割补法求面积】求下列各图中阴影部分的面积(图中长度单位为 cm ,圆周率按 3 计 算):
3
⑴
4
⑵
1
2
1
⑶
1
⑷
【解析】⑴ 4.5 ⑵ 4 ⑶1 ⑷ 2
3.【差不变】三角形 ABC 是直角三角形,阴影 I 的面积比阴影 II 的面积小 25cm2 , AB 8cm ,求 BC 的长度.
5
【解析】根据题意可知,挖去的 6 个边长 1 厘米的正方体相互之间是独立的,所以挖 去之后,原正方体的表面积相当于增加了六个小正方体的侧面积,所以现在它的表面 积为: 4 4 6 11 4 6 120 平方厘米. 16.【共高模型】如图,把四边形 ABCD 的各边都延长 2 倍,得到一个新四边形 EFGH 如果 ABCD 的面积是 5 平方厘米,则 EFGH 的面积是多少平方厘米?
【解析】该图形的上、左、前三个方向的表面分别由 9、7、7 块正方形组成.
该图形的表面积等于 (9 7 7) 2 46 个小正方形的面积,所以该图形表面积 为 46 平方厘米.
21.【取特殊点】长方形 ABCD 的面积为 36, E 、 F 、 G 为各边中点, H 为 AD 边上任 意一点,问阴影部分面积是多少?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等量代换代求面积和差不变原理练习题
1.左下图中,等腰直角三角形ABC的腰为10厘米,以C为圆心、CF为半径画弧线EF,组成扇形CEF。
如果图中甲、乙两部分的面积相等,那么扇形所在的圆的面积是多少?
2.右上图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积。
3.左下图中,扇形ABD的半径是4厘米,甲比乙的面积大3.44厘米2。
求直角梯形ABCD的面积。
(π=3.14)
4.在右上图的三角形中,D,E分别是所在边的中点,求四边形ADFE的面积。
5.下页左上图中,矩形ABCD的边AB为4厘米,BC为6厘米,三角形ABF比三角形EDF的面积大9厘米2,求ED的长。
6.右上图中,CA=AB=4厘米,三角形ABE比三角形CDE的面积大2厘米2,求CD的长。
影部分的面积和。
用割补法求面积练习题
1.求下列各图中阴影部分的面积:
(1)(2)
2.以等腰直角三角形的两条直角边为直径画两个半圆弧(见下图),直角边长4厘米,求图中阴影部分的面积。
3.在左下图所示的等腰直角三角形中,剪去一个三角形后,剩下的部分是一个直角梯形(阴影部分)。
已知梯形的面积为36厘米2,上底为3厘米,求下底和高。
4.在右上图中,长方形AEFD的面积是18厘米2,BE长3厘米,求CD的长。
5.下图是甲、乙两个正方形,甲的边长比乙的边长长3厘米,甲的面积比乙的面积大45厘米2。
求甲、乙的面积之和。
6.求下图(单位:厘米)中四边形ABCD的面积。
