11-宽化效应及卷积关系
机械测试技术习题

机械测试技术习题⼀、填空题(每空1分,共20分)1、周期信号的频谱是离散的,⽽⾮周期信号的频谱是连续的。
3、两个时域函数1()x t 、2()x t 的卷积定义为 12()()x t x t d ττ-? 。
5、测试系统的静态特性指标有灵敏度、线性度、回程误差。
6、滤波器的频率分辨⼒主要由其带宽决定。
7、对于理想滤波器,滤波器因数λ= 1。
8、半导体应变⽚是根据压阻效应原理⼯作的。
9、传感器按⼯作原理可分为应变式、电容式、电感式、压电式等。
10、⽯英等晶体沿⼀定⽅向施加外⼒使之变形时,晶体内产⽣极化,使得表⾯出现电荷,形成电场。
当外⼒去掉时,表⾯⼜重新回复到原来不带电状态,这种现象称为正压电效应。
11、根据载波受调制的参数的不同,调制可分调幅、调频、调相。
12.电感式传感器常可分为⾃感式、互感式等。
⼀、填空(1×20)1.连续3. 12()()x t x t d ττ-?5. ⾮线性度、灵敏度、回程误差6. 带宽7.18. 压阻效应9.应变式、电容式、电感式、压电式、(或热电式等)10.正压电效应11.调幅、调频、调相12磁阻式、电涡流式、(或差动变压器式)2、δ函数的频谱是均匀谱。
3、周期信号可按三⾓函数分解成下列形式:)cos cos ()(0010t n b t n a a t x n n n ωω++=∑∞=,其中,0a = ,n a = ,n b = 。
4、使信号中特定的频率成分通过,⽽衰减其他频率成分的电路称滤波器。
5、信号可分为确定性信号和随机信号,也可分为模拟信号和数字信号。
6、滤波器的品质因素Q 与带宽B 的关系是。
7、对于实际滤波器,滤波器因数λ范围⼀般是(1,5)。
8、⾦属应变⽚是根据应变效应原理⼯作的。
9、传感器按结构可分为结构型、物性型等。
11、根据滤波器的选频作⽤分,滤波器可分为低通、⾼通、带通、带阻。
12.信号分析的⼿段主要有相关分析、功率谱密度分析等。
2.均匀谱 ;sin )(;cos )(;)(2/2/022/2/022/2/10---===T T T n T T Tn T T T tdt n t x b tdt n t x a dt t x a ωω4.滤波器5.随机、数字6. 0f Q B =7. (1,5)8.应变效应9.结构型、物性型 11.低通、⾼通、带通、带阻12.相关分析、功率谱密度分析⼀、填空题(每空0.5分,共15分)2、均⽅值Ψx2表⽰的是信号的强度,它与均值µx、⽅差ζx2的关系是¢x2=H x2+óx2。
机械工程测试技术基础课后习题答案

第一章习题一、选择题1.描述周期信号的数学工具是( )。
A.相关函数B.傅氏级数C. 傅氏变换D.拉氏变换2. 傅氏级数中的各项系数是表示各谐波分量的( )。
A.相位B.周期C.振幅D.频率3.复杂的信号的周期频谱是( )。
A .离散的 B.连续的 C.δ函数 D.sinc 函数4.如果一个信号的频谱是离散的。
则该信号的频率成分是( )。
A.有限的B.无限的C.可能是有限的,也可能是无限的5.下列函数表达式中,( )是周期信号。
A. 5cos10()0x t ππ ≥⎧= ⎨≤⎩当t 0当t 0 B.()5sin2010cos10)x t t t t ππ=+ (-∞<<+∞ C.()20cos20()at x t e t t π-= -∞<<+∞6.多种信号之和的频谱是( )。
A. 离散的B.连续的C.随机性的D.周期性的7.描述非周期信号的数学工具是( )。
A.三角函数B.拉氏变换C.傅氏变换D.傅氏级数8.下列信号中,( )信号的频谱是连续的。
A.12()sin()sin(3)x t A t B t ωϕωϕ=+++B.()5sin 303sin 50x t t t =+ C.0()sin at x t e t ω-=⋅9.连续非周期信号的频谱是( )。
A.离散、周期的B.离散、非周期的C.连续非周期的D.连续周期的10.时域信号,当持续时间延长时,则频域中的高频成分( )。
A.不变B.增加C.减少D.变化不定11.将时域信号进行时移,则频域信号将会( )。
A.扩展B.压缩C.不变D.仅有移项12.已知 ()12sin ,()x t t t ωδ=为单位脉冲函数,则积分()()2x t t dt πδω∞-∞⋅-⎰的函数值为( )。
A .6 B.0 C.12 D.任意值13.如果信号分析设备的通频带比磁带记录下的信号频带窄,将磁带记录仪的重放速度( ),则也可以满足分析要求。
卷积积分与离散卷积--方波序列和方波序列的卷积及卷积过程演示

1引言信号的卷积是针对时域信号处理的一种分析方法,信号的卷积一般用于求取信号通过某系统后的响应。
在信号与系统中,我们通常求取某系统的单位冲激响应,所求得的h(k)可作为系统的时域表征。
任意系统的系统响应可用卷积的方法求得。
离散时间信号是时间上不连续的“序列”,因此,激励信号分解为脉冲序列的工作就很容易完成,对应每个样值激励,系统得到对此样值的响应。
每一响应也是一个离散时间序列,把这些序列叠加既得零状态响应。
因为离散量的叠加无需进行积分,因此,叠加过程表现为求“卷积和”。
LabVIEW是一种程序开发环境,由美国国家仪器(NI)公司研制开发的,类似于C和BASIC开发环境,但是LabVIEW与其他计算机语言的显著区别是:其他计算机语言都是采用基于文本的语言产生代码,而LabVIEW使用的是图形化编辑语言G编写程序,产生的程序是框图的形式。
本课程设计就是利用LabVIEW软件来实现方波序列卷积的过程,然后对方波序列移位过程进行演示,通过卷积过程演示和卷积和的波形图可以看出,方波序列的幅值大小不会影响卷积和的宽度而方波序列的宽度大小就会影响卷积序列相交部分的范围宽度即卷积宽度。
通过labview你能直观清晰地观察卷积的过程。
2虚拟仪器开发软件LabVIEW8.2入门2.1 LabVIEW介绍LabVIEW(Laboratory Virtual Instrument Engineering Workbench)是一种用图标代替文本行创建应用程序的图形化编程语言。
传统文本编程语言根据语句和指令的先后顺序决定程序执行顺序,LabVIEW 则采用数据流编程方式,程序框图中节点之间的数据流向决定VI及函数的执行顺序。
VI指虚拟仪器,是 LabVIEW]的程序模块。
LabVIEW 提供很多外观与传统仪器(如示波器、万用表)类似的控件,可用来方便地创建用户界面。
用户界面在 LabVIEW中被称为前面板。
使用图标和连线,可以通过编程对前面板上的对象进行控制。
数字信号处理课件第十章--利用离散傅里叶变换的信号傅里叶分析(ppt文档)

问DFT的样本数N为多少?即,v[n]的长度 = x[n]截取的长度 ΔΩ = Ωk – Ωk-1 = 2π/NT ≤ 2π(10)
有 N ≥ 500
取N = 512 ----- Δf = 9.77Hz
考虑:采样频率、数据长度、频率分辨率之间的关系 (在不产生混叠情况下)
分辨率 窗函数W(ejω)的主瓣宽度 窗的长度L 泄漏 窗函数W(ejω)的主瓣和旁瓣的相对幅度 窗的形状
矩形窗
Wr (e j )
L1
e jn
n0
e j( L1)/2
sin[L / 2] sin( / 2)
主瓣最窄,但旁瓣幅度最大
Kaiser窗
wk
[n]
如:语音信号的频率成分 ----- 发声的物理器官,声腔的谐振(识别 与建模)
机器设备振动信号的频率分析----- 产生各种振动的部件,转 子、轴承、齿轮、箱体的振动与谐振(故障诊断)
Doppler雷达系统的频率分析 ------ 频移表示目标的速度
(3)对信号,信号的分析和特征(提取) 例: 语音信号
2
2
A1 w[n]e j1e j1n A1 w[n]e j1e j1n
2
2
由频移特性,得加窗序列的傅立叶变换
V (e j ) A0 e W j0 (e j(0 ) ) A0 e W j0 (e j(0 ) )
2
2
A1 e W j1 (e j(1) ) A1 e W j1 (e j(1) )
第二个问题:
Ω与ω ------ ω = ΩT
------ 频率归一化
几种线形之间的关系
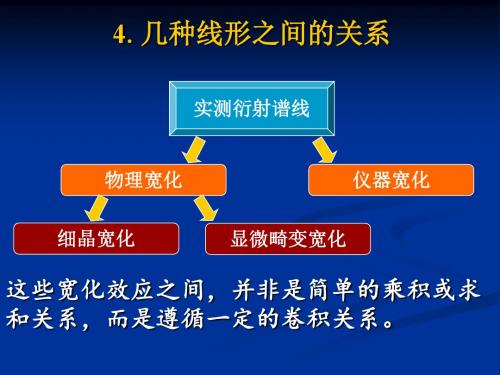
按上述思路,可以建立起三个线形函数之 间的卷积关系:
h( x) g ( y) f ( x y)dy
实测线形h(x)通过实际测量获得; 仪器宽化线形g(x)通过无物理宽化的标 样来测得; 通过函数分离确定出未知的物理宽化线 形f(x)。
三个线形的积分宽度之间的关系:
三个积分宽度的 卷积关系:
B b
g ( x) f ( x)dx
实测线形函数h(x) —————B 仪器宽化线形函数 ———b g(x) ———β 物理宽化线形函数f(x)
细晶宽化与显微畸变宽化的卷积关系
物理宽化线形函数f(x) 晶粒细化线形函数M(x) 显微畸变线形函数N(x)
d n 4 tan d 观察物理宽化β 随θ 角的变化规律:
2 tg 2 1 tg1
2 cos1 1 cos 2
K m D cos
主要是由晶格畸变引起的宽化 主要是由晶粒细化引起的宽化
若介于两者之间,是两种因素引起的宽化
晶粒细化宽化和显微畸变宽化的分离
两边同乘 cos2
2
2 K d 2 sin 2 2 ( ) 2 ( ) (4 ) D d
cos
作图(
cos
2 d K ) 2 ~ (4 ) 2,斜率为( ) 2,截距 2 d D
sin
1 1 1 x
2
, N ( x)
1 1 2 x
2
,
则: m n
K d m , n 4 tan D cos d K d 4 tan D cos d cos 两边同乘 cos K d sin 4 D d
第一章 傅里叶分析

第一章主要内容
1、常用函数
2、卷积和相关 3、空间频率及空间频谱 4、傅里叶级数 5、傅里叶变换
本章教学目标
1、本章及下一章内容都将介绍傅里叶光学中基础理论, 包括常用函数、常见的光学运算,以及傅里叶变换方 法和线性系统理论。
圆孔光瞳的非相干脉冲响应 以及圆孔的夫琅和费衍射图样
1、一些常用函数
需要特别说明的是,上面提到的常用函数有的本身就是二维函
数,而那些只给出一维形式的函数也具有二维形式,这里不再赘 述,只给出这些常用二维函数的图形化表示。 二维矩形函数
x x0 y y 0 x x0 y y0 rect ( , ) rect ( )rect ( ) b d b d
x y Circ r0
2 2
应用
1 0 x 2 y 2 r0 others
常用来表示圆孔的透过率。
1、一些常用函数 * 8)斜坡函数( Ramp function) 定义 应用
x x0 常用来表示边界透过率的灰阶变化。 0, x x0 b b ram p( ) x x0 x x0 b , b b b
( x n, y m) comb x comb y
n m
( x na, y mb)
1 x y comb comb ab a b
应用 常用二维梳状函数表示点 光源阵列或小孔阵列的透 过率函数。
1、一些常用函数
二维高斯函数
Gauss( x x0 y y0 x x0 y y0 , ) Gauss( )Gaus( ) b d b d
铜薄膜微结构的X射线衍射线形分析
铜薄膜微结构的X射线衍射线形分析龙梦龙;庞娜;陈冷【摘要】首先采用真空蒸镀法制备了不同厚度的铜薄膜,并对薄膜进行了退火处理;然后用X射线衍射仪测定铜薄膜的衍射谱,最后采用线形分析法对衍射谱进行计算,得到了不同厚度铜薄膜退火前后的晶粒尺寸和微应变。
结果表明:真空蒸镀铜薄膜晶粒尺寸随薄膜厚度的增加而增大,微应变随薄膜厚度的增加而减小;退火处理后薄膜晶粒明显长大,薄膜微应变在退火处理后明显减小。
%Copper thin films with diffrent thickness were prepared by method of physical vapor deposition (PVD), and then the films were annealed in vacuum environment. The X-ray diffraction spectrum were measured by X-ray diffractometer and analyzed by line profile analysis to calculate the crystalline size and microstrain of the prepared copper thin films before and after annealing. The results show that with the increase of the thin film thickness, the crystalline size increased and the microstrain decreased. And after annealing, crystalline size of the thin films obviously grew and the microstrain obviously reduced.【期刊名称】《理化检验-物理分册》【年(卷),期】2012(048)008【总页数】4页(P508-511)【关键词】铜薄膜;X射线衍射线形分析;晶粒尺寸;微应变【作者】龙梦龙;庞娜;陈冷【作者单位】北京科技大学材料科学与工程学院,北京100083;北京科技大学材料科学与工程学院,北京100083;北京科技大学材料科学与工程学院,北京100083【正文语种】中文【中图分类】TB31铜因具有良好的化学稳定性和电特性,在电子工业中应用日渐广泛。
衍射线线形分析方法
衍射线线形分析方法一、衍射线的线形1. 衍射线的线位2. 衍射线的强度3. 衍射线的宽度二、衍射线线形分析1. 吸收因子、温度因子和角因子的影响2. K α双线分离3. 仪器宽化效应3. 物理宽化效应三、微晶宽化与微观应力宽化的分离一、衍射线的线位衍射线的线形:指衍射线强度按衍射角2θ的分布。
1. 衍射线的线位(1)图形法:直接从衍射线图形出发确定线位的方法延长线法:延长衍射线顶部两侧的直线部位,两虚线交于A点。
过A点作背底的垂线,对应的2θ数值为衍射线的线位。
顶点法:从衍射线的最高点B作背底的垂线,对应的2θ数值为衍射线的线位。
弦中位法:在最大强度的3/4、2/3、1/2处做平等于背底的弦,从弦的中点作背底的垂线,对应的2θ数值为衍射线的线位。
背底的扣除:测得衍射线的线形后,在作各种数据处理前必须首先扣除背底。
当衍射峰比较尖锐时,作连接线形两侧根部平缓区的直线即可扣除背底当衍射峰比较漫散,难以确定衍射线两侧的平底时,可用标准物质的背底作为样品测量的背底(2)曲线近似法最常用的方法是将衍射线顶部(强度>85%部分)近似为抛物线,再用3~5 个实验点拟合此抛物线,此抛物线顶点对应的2θ数值为衍射线的线位。
在衍射线顶部等间隔取三个实验点如果等间隔取五个实验点,称为五点抛物线近似法,线位2θp为:抛物线近似法常用于峰-背比较高且峰位处较光滑的衍射线。
(3)重心法取衍射线重心所对应的2θ数值为衍射线的线位,记为<2θ>。
将衍射峰所在2 θ区间分为N 等分:利用了全部衍射数据确定衍射线的线位,所得结果受其它因素干扰较小,重现性好,但工作量大,适用于计算机机数据联机。
2. 衍射线的强度(1)峰高强度以衍射线的峰高代表衍射线的强度,以衍射谱中最高峰强度定为100,并以此确定其它峰的强度。
(2)积分强度以衍射线以下、背底以上的面积代表衍射线的强度。
3. 衍射线的宽度(1)半高宽度在衍射线最大强度的一半处作平行背底的弦,用此弦长代表衍射线的宽度。
晶块尺寸及晶格畸变测定
−∞
+∞
衍射峰物理宽化的测定 —— 近似函数法
积分宽度的卷积关系 令 β——物理因素的积分宽度 b——仪器因素的积分宽度 B——合成峰的积分宽度 可得
bβ B = +∞ ∫ g(x) f (x)dx
−∞
衍射峰物理宽化的测定 —— 近似函数法
欲利用上式求得物理加宽,必须先给定g(x)和f(x)函 数的具体表达式。 g(x)和f(x)的近似函数通常从下列三种函数中选取:
如图,衍射线半高宽为:
β = 2(θ + ∆θ1/ 2 ) − 2(θ − ∆θ1/ 2 ) = 4∆θ1/ 2
对Bragg方程微分得:
∆θ1/ 2 = −tgθ ⋅ ∆d d
所以
∆d β = 4tgθ ⋅ d
Kα双线分离
Kα双线对衍射峰位、线形和积分宽度都有影响,为了 得到单一的Kα1衍射峰,需用数学方法从Kα双峰中分离 出单一的Kα1衍射峰。
Hall-Williamson关系:由晶块细化和晶格畸变导致的衍 关系: 关系 射峰宽化(随着衍射角增大展宽变大)遵循下列关系: 射峰宽化(随着衍射角增大展宽变大)遵循下列关系:
βicosθi=kλ/D+2εsinθi
作βicosθi ~ sinθi 直线,利用截距求晶块尺寸 ,用斜率 θ θ 直线,利用截距求晶块尺寸D, 求晶格畸变ε 求晶格畸变ε。
卷积和相关
都是两个函数通过某种运算得到另一函数。 一个函数是输入函数(待观测量、输入信号), 一个函数描述观测方式或观测仪器的特征(或作用 特点) 另外一个函数就是输出函数(信号),即观测得到 的结果。 “某种运算”:就是观测方式或观测仪器对输入 函数作用的数学描述。
平移量等于两者的平移量之和。
8、函数 f ( x, y) 与
d
函数的卷积
根据 1. d-函数是偶函数, 2. d-函数的筛选性质, 有:
f ( x) d ( x) f ( )d ( x )d f ( x)
即任意函数与d(x) 卷积后不变 利用卷积的位移不变性可得:
g(x)称为函数f(x)与h(x)的卷积. 二维函数的卷积:
g ( x, y ) f ( x, y ) h ( x, y )
f ( , )h( x , y )d d
三、卷积的物理意义和几何意义
物理意义:像强度分布是物强度分布与单位强度点 光源对应的像强度分布的卷积.
若右边园孔上加p 位相板, 则 t (x, y)
=
x2 y2 circ l/2
*
d (x+d/2 - d (x-d/2)]
练习 1-12
若f(x) * h(x) = g(x), 证明 (1) f(x- x0) * h(x) = g(x - x0) (2) h(x) * f(x) = g(x)
卷积运算:可用来表示一个观测系统或一个 观测仪器对输入信号的作用过程,等等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
θ
各亚晶块同族晶面具有一系列不同的晶面间 距,衍射线将合成一定范围内的宽化谱线。 晶面畸变的相对变化量服从统计规律且没有 方向性,即显微畸变造成的宽化效应,峰值位 置并不改变。
θ
试样
光源
狭缝
(2) 实际材料内部组织结构所导致的物理宽 化效应。凡是破坏晶体完整性的因素, 均导致衍射谱线宽化。
(3) 衍射线形中 Kα 双线及有关强度因子等所 导致的宽化效应。
Kα
1
Kα
2
真实线形或物理线形,是反映材料内部真实 情况的衍射线形,仅与材料组织结构有关。 这种线形虽无法利用实验手段来直接测量, 但可以通过各种校正及数学计算,从实测线形 中将其分离出来。 这就是衍射线形分析的目的。
细晶宽化函数m(x)积分宽度为βD ,显微畸变 宽化函数n(x)积分宽度为βε ,它们与物理宽化 函数f(x)积分宽度β的卷积关系为
D
m( x)n( x)dx
实测线形函数h(x)积分宽度(综合宽度)表示为 B,标样衍射线形函数g(x)积分宽度(仪器宽度) 为b,真实物理线形函数f(x)积分宽度(真实宽度) 为β。 可以证明,三个积分宽度的卷积关系为
B b
g ( x) f ( x) dx
(2) 细晶宽化与显微畸变宽化的卷积关系
在真实物理宽化线形函数中,包括了全部与 材料组织结构有关的宽化衍射信息。 若物理线形只包含了细晶宽化及显微畸宽化 效应,则物理宽化函数f(x)与细晶宽化函数m(x) 和显微畸变宽化函数n(x)的卷积关系为
式中,综合实测线形h(x)可通过实际测量来获 得,几何线形g(x)可通过无物理宽化的标样来 测得。 因此,这三个函数中有两个是已知的,通过 函数分离即可确定出未知的物理线形f(x)函数。
分别定义这三个函数的积分宽度。积分宽度 等于衍射峰形面积除以曲线的最大值,积分宽 度虽不等于谱线强度的半高宽度,但与半高宽 度成正比。
(1) 几何宽化与物理宽化的卷积关系
引入三个重要的线形函数,即实测线形函数 h(x)、几何线形函数g(x)以及物理线形函数f(x)。 三个函数都规定x=0时为最大值1,这样将给 分析和计算带来方便。
实测线形函数,反映的是试样实际X射线衍 射谱线,包含了全部衍射线形宽化效应。 几何线形函数,则仅是仪器参数所造成的几 何宽化线形。 物理线形函数仅代表与材料组织结构有关的 真实线形。 物理宽化因素影响下进一步增宽,同时峰 值降低,即物理宽化因素不改变整个衍射曲 线的积分强度(积分面积)。
图中给出这些因素的六种近似函数形状,称 为衍射仪的权重函数。 如果只考虑 g1~g5 五个因素,许多情况下的 合成函数与实测标样线形并不一致。为此引入 不重合函数 g6,使最终线形与实际相符。
3、物理宽化效应
衍射谱线的物理宽化效应,主要与亚晶块 尺寸(相干散射区尺寸)和显微畸变有关。 亚晶块越细或显微畸变越大,则X射线衍射 谱线越宽。 此外,位错组态、弹性储能密度及层错等, 也具有一定的物理宽化效应。
(1) 细晶宽化
对于多晶试样而言,当晶块尺寸较大时,与 每个晶块中的某一晶面{hkl}相应的倒易点近似 为一几何点。 由无数晶块中同族晶面{hkl}相应的点组成了 一个无厚度的倒易球面。
材料中亚晶块尺寸较小时,相应于某晶面组 {hkl}的倒易点扩展为倒易体,则由无数亚晶块 相应的倒易体组成了具有一定厚度的倒易球, 即衍射畴与反射球相交的范围也就越大。 此时在偏离布拉格角的方向上也存在衍射现 象,造成衍射线的宽化。
如图所示,将几何宽化线形曲线下的面积分 成若干无穷窄的长条面积元,各面积元按物理 宽化线形函数展宽且面积不变。 将这些展宽线形函数进行叠加,即得到综合 实测线形h(x)。
按照上述思路,可以建立三个函数之间的卷 积关系,如下等式
h( x) g ( y) f ( x y) dy
h( x) g ( y) f ( x y) dy
Scherrer公式,可表示为
D 0.89 cos cos
式中积分宽度β的单位为弧度,D为亚晶块尺寸, λ为射线波长。 该晶粒尺寸测量值,仅代表晶粒沿试样法线 方向的尺寸。
需要说明,一个晶粒中包含多个亚晶粒,晶 粒尺寸测量值,实际是晶粒中的亚晶粒尺寸。
(2) 显微畸变宽化
通过理论分析,可以推导出显微畸变为
cot 4
式中积分宽度β的单位为弧度。 该显微畸变,仅代表晶粒沿试样法线方向 的显微畸变。
(3) 其它宽化效应
除了细晶与显微畸变因素外,晶体中的各类 缺陷也可导致谱线宽化效应,包括空位、间隙 原子、位错、层错等。
4、谱线卷积关系
实测衍射谱线中同时存在几何宽化与物理宽 化效应,而真实衍射谱线中又同时存在细晶宽 化与显微畸变宽化效应等。 这些线形宽化效应之间,并非是简单乘积或 求和的关系,而必须是遵循一定的卷积关系。
2、几何宽化效应
几何宽化效应也称仪器宽化效应,主要与光 源、光栏及狭缝等仪器实验条件有关。 例如X射线源具有一定几何尺寸、入射线发散、 平板样品聚焦不良、接收狭缝较宽及衍射仪调 正不良等,均造成谱线宽化。 即使是其它实验条件都相同,仅接收狭缝发 生变化,同一试样的衍射谱线则存在很大区别。 如果采用不同仪器测试,对于同一试样的相 同衍射面,且狭缝参数完全相同,测得的衍射 谱线也有所不同。
f ( x) m( y) n( x y) dy
f ( x) m( y) n( x y) dy
式中物理宽化函数f(x)是从式(3)中分离出的,即 f(x)可以确定。 然而,细晶宽化函数m(x)和显微畸变宽化函数 n(x)均未知,甚至这两个函数的具体形式都无法 确定,给分离带来一定难度。
衍射谱线宽化效应及卷积关系
Hale Waihona Puke 姜传海 上海交通大学材料科学与工程学院
宽化效应及卷积关系
1、影响谱线宽度的主要因素
2、几何宽化效应
3、物理宽化效应
4、谱线卷积关系
1、影响谱线宽度的主要因素
实测线形或综合线形,是由衍射仪直接测得 的衍射线形,影响因素主要包括: (1) 仪器光源及衍射几何光路等实验条件所 导致的几何宽化效应;
