带启动时间的N_策略M_G_1排队
MG1型排队系统分析与仿真

M/G/1型排队系统分析与仿真一、排队系统排队论(queuing theory), 或称随机服务系统理论, 是通过对服务对象到来及服务时间的统计研究,得出这些数量指标(等待时间、排队长度、忙期长短等)的统计规律,然后根据这些规律来改进服务系统的结构或重新组织被服务对象,使得服务系统既能满足服务对象的需要,又能使机构的费用最经济或某些指标最优。
它是数学运筹学的分支学科。
也是研究服务系统中排队现象随机规律的学科。
广泛应用于计算机网络, 生产, 运输, 库存等各项资源共享的随机服务系统。
排队论研究的内容有3个方面:统计推断,根据资料建立模型;系统的性态,即和排队有关的数量指标的概率规律性;系统的优化问题。
其目的是正确设计和有效运行各个服务系统,使之发挥最佳效益。
一般的排队过程为:顾客由顾客源出发,到达服务机构(服务台、服务员)前,按排队规则排队等待接受服务,服务机构按服务规则给顾客服务,顾客接受完服务后就离开。
排队过程的一般过程可用下图表示。
我们所说的排队系统就是指图中虚线所包括的部分。
排队系统又称服务系统。
服务系统由服务机构和服务对象(顾客)构成。
服务对象到来的时刻和对他服务的时间(即占用服务系统的时间)都是随机的。
描述一个排队系统一般需要分析其三个组成部分:输入过程、排队规则和服务机构。
输入过程输入过程考察的是顾客到达服务系统的规律。
它可以用一定时间内顾客到达数或前后两个顾客相继到达的间隔时间来描述,一般分为确定型和随机型两种。
例如,在生产线上加工的零件按规定的间隔时间依次到达加工地点,定期运行的班车、班机等都属于确定型输入。
随机型的输入是指在时间t内顾客到达数n(t)服从一定的随机分布。
如服从泊松分布,则在时间t内到达n个顾客的概率为或相继到达的顾客的间隔时间T 服从负指数分布,即式中λ为单位时间顾客期望到达数,称为平均到达率;1/λ为平均间隔时间。
在排队论中,讨论的输入过程主要是随机型的。
排队规则排队规则分为等待制、损失制和混合制三种。
五节MG1排队模型

以上讨论了M/M/1和M/M/C系统 ,其 前提均为泊松输入和负指数服务处理,这 类系统的工具是生灭工程状态转移图。在 实际中,有时到达仍为泊松过程 ,但服务 时间并不服从负指数分布,即M/G/1系统 这时不能用生灭过程处理,而主要依据布 拉切克-钦辛公式(P-K公式)。
一.(M/G/1) : ( / ∞/G)系统 ∞
∴
Lq λ λ2 λ Lq = Ls − = , Wq = = µ 2µ ( µ − λ ) λ 2µ ( µ − λ ) 均为M / M /1相应指标的一半。
可见,内部越有规律越省时间
三.(M/Ek /1 ):(∞ / ∞ /G)系统 (k阶爱尔郎服务时间)
设 υ = ∑υi,每个υi 服从同参数的负指数分布
由 特 式 里 公 : W = S LS , q =W − E υ),Lq = λW W ( S q
λ
二.(M/D/1):( ∞/ ∞ /G)系统 (定长服务时间)
2 这时υ ≡ E υ), σ(υ) 0 ( =
∴
Ls = ρ +
1
ρ
2
若设 : E (υ ) =
µ
2 (1 − ρ ) λ λ2 则 Ls = + µ 2µ (µ − λ )
i =1 k
于是E (υ ) =
1
µ
,σ 2 (υ ) =
1 kµ
,令ρ =λ E υ)= ( 2
由P-K公式:
λ Ls = + µ
λ (
2
1
µ
2
+
1
λ µ
2(1 −
由里特公式:
Lq Ls (k + 1) ρ Lq = ,Ws = ,Wq = 2k (1 − ρ ) λ λ
非强占有限优先权M-G-1排队系统

非强占有限优先权M/G/1排队系统>针对部分数据帧有完全优先权发送的计算机网络数据服务系统存在的网络拥塞风险问题,提出了一种非强占有限优先权M/G/1排队系统模型的方法。
该系统模型引入控制完全优先权的参数n,使得数据帧的完全优先权变成有限优先权,考虑了不同优先级队伍之间的公平性,降低了计算机网络数据服务系统拥塞的风险,使得网络系统在有限优先权下有较好的稳定性。
在模型研究中,运用全概率拆解方法获得各级队伍平均等待时间、平均逗留时间和平均队长的理论结果。
对模型采用Matlab 2010a软件实验仿真,实验得到的各级队伍平均等待时间和理论平均等待时间的平均绝对误差为0.951%。
实验中,有限优先权条件下各级顾客的平均等待时间比值显著小于完全优先权条件下各级顾客的平均等待时间比值。
实验结果表明对非强占有限优先权M/G/1排队系统模型研究的理论结果是正确的,该模型具有更稳定的系统特性。
0引言排队论是运筹学的分支,其理论得广泛应用于计算机网络数据发送服务[1]、通信系统[2]、道路交通[3]、银行[4]、地铁[5]、医院[6]等一些服务领域。
对不同领域的服务系统需要建立与之对应的排队系统模型进行研究。
当前已有很多文献对排队系统进行过深入研究。
文献[7]对强占及非强占优先权排队系统作了基础研究;文献[8]研究了非强占优先权的多服务器排队系统,将非强占优先权排队系统服务器扩充到多台经行研究;文献[9]引入绩效评价将排队系统应用在银行自动取款机(Automatic Teller Machine, ATM)系统,展示排队论在其他领域中有效的应用,此后排队论更是广泛应用于各种服务领域之中。
之后研究人员纷纷研究了多级适应性M/G/1可修排队系统[10]、M/G/1休假排队系统[11]、基于多重休假的min(N,V)策略M/G/1排队系统[12]等。
现在文献对休假排队系统和可修排队系统研究颇多,其排队系统在计算机网络[13]和通信领域[14]也有较好的应用,但对于计算机网络应用中待解决的优先权拥堵问题相关文献比较少[15]。
马尔可夫链的定义及例子

3、转移概率
定义 i, j S, 称 P Xn1 j Xn i
的一步转移概率。
pij n 为n时刻
若i, j S, pij n pij ,即pij与n无关,称转移概率
具有平稳性.此时称{Xn,n≥0}为齐次(或时齐的)马尔 可夫链。记P=(pij),称P为{Xn,n≥0}的一步转移概率矩阵.
0
j!
j 0,1, i
pi0公式略有不同,它是服务台由有i个顾客转为空闲的
概率,即第n个顾客来到时刻到第n+1个顾客来到时刻之
间系统服务完的顾客数≥i+1。
pi0 P X n1 0 X n i P(Yn i 1) P(Yn k) k i1
et (t)k dG t ,
0 P{Yn
j Tn1 x}dG x
( x) j exdG x, j 0,1, 2,
0 j!
因此, {Xn,n≥1}是马尔可夫链。其转移概率为
P0 j P( X n1 j X n 0) P(Yn j X n 0)
P(Yn
P( X n1 in1 X n in )
所以{Xn,n≥0}是马尔可夫链,且
pij P( X n1 j X n i) P( f i,Yn1 j) P( f i,Y1 j)
二、切普曼-柯尔莫哥洛夫方程
1,随机矩阵 定义:称矩阵A=(aij)S×S为随机矩阵,若aij ≥0,且
一步转移概率矩阵
0.5009
0.0458 0.2559 0.1388 0.2134
0.0466 0.0988 0.36584 0.14264
【国家自然科学基金】_m_g_1排队系统_基金支持热词逐年推荐_【万方软件创新助手】_20140801
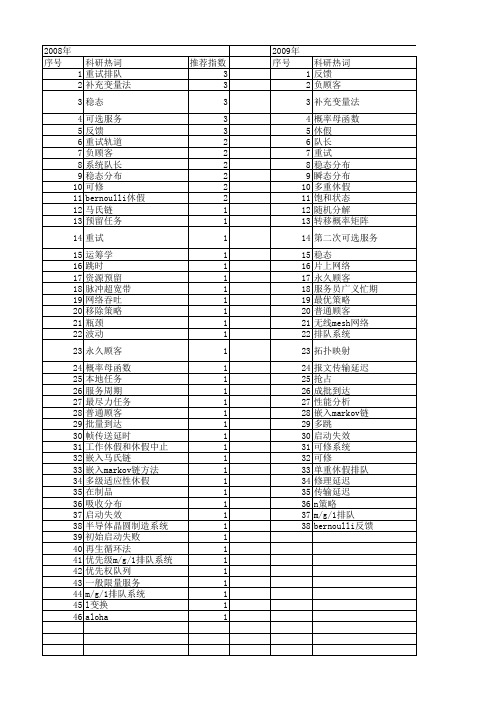
推荐指数 3 3 3 3 3 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
53 54 55 56 57 58 59 60 61
2011年 科研热词 推荐指数 随机分解 5 排队论 4 多重休假 4 启动-关闭期 3 n策略 3 队长分布 2 队长 2 时间依赖解 2 全概率分解技术 2 齐次可列半马尔可夫过程 1 预解集 1 集装箱码头闸口 1 闸口通过能力 1 重试排队 1 递推公式 1 适定性 1 负顾客 1 谱 1 自相似业务 1 置信区间 1 系统最优 1 等待时间 1 第二种服务可选的m/g/1排队模型 1 稳态队长 1 积分半群 1 离散重试排队 1 泊松分布 1 水路运输 1 未决赔款准备金 1 服务中断 1 排队长 1 排队系统 1 排队模型 1 失效次数 1 启动时间 1 启动失败 1 启动 1 向后方程组 1 向前方程组 1 吉比特无源光网络 1 可修排队系统 1 单重工作休假 1 单重休假 1 动态带宽分配算法 1 剩余寿命 1 关闭 1 休假中断 1 交通疏散 1 不可靠服务台 1 不可用度 1 p-进入规则 1 n-策略排队 1
带负顾客的N策略启动时间的Geo/Geo/1工作休假排队

Ab s t r a c t :Th i s p a p e r d e a l s wi t h a Ge o m/ Ge o m/ 1 q u e u e wi t h mu l t i p l e wo r k i n g v a c a y i o n s
i n whi c h c u s t ome r s a r e e i t he r“ po s i t i v e ’ ’o r“ ne ga t i v e ”, i n a d dt i on t o N— p ol i c y .n e g a t i v e
文章编号 : 1 6 7 2 — 6 9 8 7 ( 2 0 1 3 ) 0 2 — 0 2 1 6 — 0 5
带 负顾 客 的 N 策 略启 动 时 间的 Ge o / G e o / 1工 作 休 假 排 队
郭 宏侠 。 徐秀 丽 。 耿 杰
( 燕 山 大学 理 学 院 , 河北 秦皇岛 0 6 6 0 0 4 )
法得 到 队 长 的 稳 态 分 布 , 进 一步得 出 了系统队 长的 随机分 解 的结果 。
关键 词 :工作休假 ; N 策略 ; 启 动 时间 ; 矩 阵几何解 ; 条件 随机 分 解
中图分 类号 : O 2 2 6 文献标 志码 : A
G e o / Ge o / 1 Wo r k i n g Va c a t i o n Qu e u e wi t h N- P o l i c y a n d
摘 要 :研 究 了正 、 负两 类顾 客 的 离散 时 间 Ge o / Ge o / 1多重 工作 休 假 排 队 模 型 , 并 加 入 N 策略 和启动 时 间 , 负顾 客 不接 受服 务 , 并 只起 一 对 一抵 消队 首 正接 受服 务 的顾 客 的 作 用, 即服从 RC H( Re mo v e c u s t o me r f r o m h e a d ) 策 略 。使 用 拟 生 灭过 程 及 矩 阵几 何 解 方
带启动时间的Geom/Geom/1多重工作休假排队
引言
在 过 去二 十多 年 以来 , 假排 队 系统得 到 了较 深入 地 研 究 , 期 ,ev 和 Fn 休 近 Sri in在 20 02年
首次提出一种半休假策略, 即工作休假 : 在休假期间, 服务员并未完全停止服务 , 而是以较低 的
速率 为顾 客提供 服务 。 田乃 硕 、 继红 等研 究 了离散 时 间 Go / em 1 重及 多重 工 作休 假 李 em G o / 单
排 队。
在一些特定的排 队系统中 , 当系统从工作休假结束进入正常服务状态时 , 需要经历一段启 动( 预热 ) 时间 , 才能开始正常服务 。本章研究的是带启动时间的离散时间多重工作休假排 队
系统 , 即带 启动 时 间 的 Go / em 1多 重 工 作 休 假 模 型 。系统 中无 顾 客 时进 人 工 作 休 假 状 em G o /
n m e f h ut esadt vr esjunt f ut rntes t nr te u bro tecs m r n eaea oor meo c s me t i a s t. o h g i a o i h ao y a Kew rs Wokn aa os St pt e G o e i slt n A eaes or A e g u bi y o d rigvctn e—u m e m tc o i vrg o un i i r uo j vr en m e a "
1 1 模 型 的描述 .
对 于任 意 的 ∈ [ ,]记 = 1一 这 里我 们讨 论 晚到 有 延 迟入 口的离 散 时 间排 队 模 01 , 。
型 , 型描述如下 : 模
( ) 客 到 达 时 间发 生在 时 隙末 端 ( 一 ) 到 达 间隔 独 立 同分 布 , 1顾 n, , 并且 服 从 参数 为 P的 几何 分 布 , 为 ; 记 服务 的 开始 和结束 都发 生 在时 隙分 点 t=/处 , I 正规 忙期 内服务 时间 和工作
带启动期GI/G/1排队的一个特殊瞬时分布
<
∞
.
5 系统 内有 一个 服务员 , 服 务服 从 先 到先 服 务 规 则 , 定 到 达 间隔 、 务 时 间 、 动 期 相 互 独 ) 且 假 服 启
立.
2 队 长
令 Lt ()是 t 时刻上述 系统 的队长 ( 即为 时刻 t 服务 台前等 待 的顾 客 数与 正 在被 服务 的顾 客数 在
0( ) t }的瞬 时分布 所满足 的方程 , 并证 明其概 率分布 是一 方程 的最 小非 负解.
[ 关键 词 ] 带启动期 的 G/ / 排 队 系统 ; 尔可夫 骨架过 程 ; 时分布 IG 1 马 瞬
[ 中图分类号] 2 [ 0 2 文献标识码] [ A 文章编号 ]63— 02 20 )6 00 — 3 17 8 1(0 7 0 — 0 6 0
维普资讯
20 0 7年 1 2月
重 庆文 理 学 院 学 报 (f然 科 学 版 ) {
Junl f hnqn nvrt o r n c ne N trl cec dt n ora o o gigU i sy f t adSi cs( a a Si eE io ) C e i A s e u n i
随着计 算机通 讯 网络的飞 速发 展 , T 异步转 换 模 式 ) A M( 技术 以其强 大 的处 理 能力 成 为支 持宽 带 综合 业务数 字业务 网( B—ID ) S N 和多媒体 通信 有效 的交换 方式 .
假定 到达 A M 网络 中 S C 基 于交换 虚通 道 ) T V C( 的需求 遵 循一 个 Psi os n过程 . asn等 把 S C o Hs a VC 归 结为一个 带启 动时 间的 M G 1 队系统 , 而给 出 了指标 分 析 , // 排 从 建立 了 S C V C的模 拟模 型. 但这 个 模 型用于 A M 网络性能分 析也有 不 足之处 . T 由于业 务 量 的到 达 具有 猝 发性 和相 关 性 , 简单 地用 Pi os —
带备用服务员及启动期和负顾客的Geo/Geo/1休假排队
<1 , 方程 A z+R A I+A o:R有最小 非负 解 ,
y 。
R =
咖
( 2)
。
0 0
面
P
6 = 0
= O O ~ ; = 詈= O l O l ~ ; f , : 6 + ( + p q ) t 一 - t b + P 一 q + P — q t ~ t h ;
第 2期
朱翼隽等 : 带备用服务员及启动期和负顾 客的 G e o / G e O / 1休 假 排 队
。8 3・
I
=
o r 一4 ( ( +P q ) +p q ) p — q l - — t b — 2 ( ( + P q ) t x — b — + p ) ; 2
—
/
由于正 、 负顾客 到达 间隔 、 服务 时 间 、 休假 和启 动 时 间都 相 互 独立 且 服 从 几何 分 布 , 所以
/L
— . . . . . . . . . . . . . . . . . . . . . . . 。 。 . . . L
—P
一g
过 程 的概率转 移矩 阵 P有 以下形式 :
等 原 因看作 是休 假 , 这 时需 要 另外 一 个售 票 员 ( 备用售票员) 上 岗接 替 服 务 , 因为 备 用售 票 员 只 是在 主
售 票员 休假 期 内服务 , 所 以规 定其 不休 假 ; 而负顾 客 可 以看 作是 部 分乘 客 , 考 虑 到 时 间或者 是 经 济上 的 因素 而选 择 飞机 或者 汽车 等交 通 方式 , 这 样 就 会 带走 部 分 坐火 车 的乘 客 , 对此 , 文献 [ 3 ] 作 了详 细 的分 析 。对 于启 动期 , 例 如打 印 机 打 印 文 件 的时 候 , 当打 印机 停 止 工 作 一 段 时 间 后 , 需 要 经 过 一 个 预 热 期 ( 启 动期 ) 才 能正 常打 印 , 对此 , 文献 [ 4— 8 ] 作 了详 细 的分析 , 但是 其 同时对 备用服 务 员和 负顾 客 的研 究 并 不多 。基 于上 述情 况 , 本 文 提 出 了一 个 带 有 备用 服 务 员 、 启 动 期 和 负顾 客 的 G e o / G e o / 1休 假排 队模
1重试排队系统的开题报告
具有循环顾客和N策略多重休假的M/G/1重试排队系统的开题报告一、研究背景排队论是一种数学模型,可用于研究等待服务的时间、队列长度和系统利用率、效率等问题,将排队系统分为单通道排队系统和多通道排队系统。
单通道排队系统是一种只有一个服务设施的系统,即G/G/1模型,其中G表示到达过程的分布,G还表示服务时间的分布,1表示服务台的个数。
M/G/1模型是单通道排队系统中的一种,其中到达过程是泊松过程,服务时间是任意分布。
在实际生活和商业中,排队系统的运用广泛。
很多企业和服务提供者都需要通过排队系统来管理客流,优化服务体验。
例如,银行、超市、餐厅和医院等都是典型的排队系统。
通过调整服务台数量、服务时间和到达过程等因素,可以提高服务效率,减少客户等待时间和排队长度,提高客户满意度。
针对排队系统的研究,一方面是为了研究系统的性能指标,并针对实际需求提出相应的优化措施,另一方面是为了开展排队系统的理论研究,更好地理解排队系统的本质。
二、研究目的本论文将研究具有循环顾客和N策略多重休假的M/G/1重试排队系统。
循环顾客是指在同一时间内,在系统内多次接受服务的顾客。
N策略是指在服务员工作的时段内设置休息规则,即每当服务员工作了n个服务时间,他/她就会休息t个单位时间长度。
多重休假是指每个服务员可以有多个休息时间段。
本研究旨在通过建立数学模型,分析该排队系统的性能指标(如等待时间、队列长度、系统利用率等),为企业和服务提供者提供优化措施和参考建议,同时还可以丰富排队系统理论的研究。
三、研究内容本研究将分为以下几个部分:1. 排队系统的建模。
首先将建立具有循环顾客和N策略多重休假的M/G/1重试排队系统的数学模型,并简要介绍模型的基本假设和符号表示法。
2. 性能指标的计算和分析。
针对该排队系统模型,将计算并分析其关键性能指标,如等待时间、队列长度和系统利用率等,并提出相应的优化措施和建议。
3. 数值模拟和结果分析。
将针对该排队系统进行数值模拟实验,并分析不同参数设置下的结果,探讨排队系统的性能特征和规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
带启动时间的N -策略M/G/1排队
申玉红
(德宏师范高等专科学校数学系,云南 潞西,678400)
【摘 要】本文研究了带启动时间的N -策略M/G/1排队,利用嵌入马氏链和母函数的方法,给出了此排队系统的稳态队长,并分析了系统的忙期、忙循环等性能指标。
【关键词】N -策略排队;启动时间;稳态队长;嵌入马氏链
1 引言
在许多实际系统中,为了降低成本,当服务系统中无顾客时应关闭服务设备.当有顾客到达再次工作时通常需要一个随机的启动时间[1]在经典排队系统中考虑启动时间已被研究过[2],在休假排队系统中,带启动时间的单重休假排队与多重休假排队已被研究[3,4],但在N -策略休假排队中还没有考虑过启动时间,本文研究了带启动时间的N -策略排队,给出了此排队系统的一些排队指标。
2 模型分析及相关记号
模型描述如下:带启动时间的N 策略M /G/1排队是指,顾客到达遵循参数为λ的Poisson 过程,服务时间服从一般分布,单服务台工作,一旦系统内无顾客,服务员立刻开始休假,直到到达的顾客数达到N ,服务员立刻开始一个随机长度的启动时间后,才能开始为顾客服务,直到服务台再次变成空闲。
假定到达间隔和服务时间相互独立,使用先到先服务规则。
相关记号及意义:记服务时间分布函数为B (t ),V (t )为启动时间分布函数,平均启动时间E (V )=∫∞0t dV (t ),以V 3(S ),B 3(s )分别表示V (t ),B (t )的拉普拉斯—斯蒂尔阶斯变换(简记为L S T ),μ-1和b (2)分别表示服务时间的一,二阶矩,服务强度ρ=
λμ。
3 稳态队长采用文献[1~5]中的嵌入马氏链和边际分析法求平均队长,以Q b 表示忙期开始时系统中的顾客数,则
P (Q b =j =V j -N =∫∞0
(λt )j -N (j -N )!e -λt dV (t ) j ≥N ,并有母函数
Q b (z )=∑∞j =N P (Q b -j )z j =∑∞j =N V j -N z j =z N V 3(λ(1-z ))
以L v 表示时刻t 排队系统中的顾客数,L n 是第n 个顾客完成服务离去后系统内顾客数。
{L n ,n ≥1}是队长过程的嵌入M arkov 链.在相继离去时刻系统中顾客数之间存在着关系式
收稿日期:2008-01-02
作者简介:申玉红(1982—
),女,山东菏泽人,德宏师范高等专科学校数学系硕士生,助教。
6
8 德宏师范高等专科学校学报 2008年第1期第17卷 No112008 vol 117
L n +1
=L n -1+A L n ≥1
Q b -1+A L n =0
其中A 是一个服务时间内到达的顾客数,有概率分布及母函数
a j = ∞0(λt )j j !
e -λt d (B )t j ≥0,A (z )=B 3(λ(1-z )){L n ,n ≥1}的转移矩阵P 为
P =h 0 h 1 h 2
h 3
a 0 a 1 a 2 a 3
a 0 a 1 a 2
a 0 a 1
…
…
…
这里
h j =P (Q b -1+A =j )=0 j <N -1∑j -N +2
j =1V i -1a j -N +2-i j ≥N -1
其中,h j 是忙期开始的第一个顾客离去时系统中恰有j 个顾客的概率。
当ρ<1时稳态分布存
在,记为π=(π0,π1……
),且满足πP =π,代入转移矩阵得出 πk =∑k +1
j =1πj a k +1-j k =0,1,…,N -2 πk =π0h k +∑k +1
j =1πj a k +1-j k ≥N -1于是{πk ,k ≥
0}的母函数是 L v (z )=∑N -2k =0z k
∑k +1j =1πj a k +1-j +∑∞k =N -1z k
(π0h k +∑k +1
j =1πj a k +1-j )=1
z (L v (z )-π0)B 3(λ(1-z ))+π0Q (z )B
3(λ(1-z ))由此解得
L v (z )=
π0(Q b (z -1)B 3(λ(1-z ))z -B 3(λ
(1-z ))使用正规化条件L v (1)=1,可确定π0=1-ρN +λE (V )
,代入前式得 L v (z )=1-ρN +λE (V )(Q b (z -1)B 3(λ(1-z ))z -B 3(λ
(1-z ))由E[L v ]=L v (z )′|z =1,两次使用罗比塔法则,得到
E[L v ]=ρ+λ2b (2)2(1-ρ)+N (N -1)+2N λE (V )+λ2[E (V )]22(N +λE (V ))4 忙期和忙循环
设D v 表示N -策略M/G/1排队的忙期.由于到达间隔的无后效性,由j 个顾客开始的忙期长度是经典M /G/1排队中忙期D 的j 重独立和D j ,现在忙期开始时系统中有Q b 个顾客,于是D v 有L S T ,D v 3(s )=Q b (D 3(s ))=D 3(s )N V 3(λ(1-D 3(s ))),其中D 3(s )是D 的L S T 。
平均忙期E[D v ]=
-D 3v (s )|′s =0=N +λE (V )μ(1-ρ)。
一个忙循环由空闲期,启动期和忙期合并而成.空闲长度由N 个到达间隔组成,服从Erl ang 分布,有均值N λ,平均启动时间为E (V ).所以忙循环的均值为
7
8 申玉红:带启动时间的N -策略M/G/1排队
T =N +λE (V )μ(1-ρ)+N λ+E (V )=N +λE (V )μ(1-ρ)
5 模型应用举例
1.我们考虑一个残品修理问题,假设某车间生产一种部件,出现的残品以容量N 积存,等待修理工进行修理,修理工除了修理工作之外,当没有积存的残品时,还要做另外一项辅助工作,当残品数量达到N 时,他才转入修理工作,而在修理之前有一段随机的修理准备时间,因此,对残品的修理工作是一个带启动时间的N -策略休假排队。
2.在A T M 通信网虚通道连接中,建立连接有两种不同的机制,其中转换式虚通道连接随需求的到达和离去而动态的建立和关闭.然而,过于频繁的建立连接,需要花费网络管理成本,为了适当减少重建连接的次数,要求到达缓冲器中的信元数必须达到某个值N ,服务器才予以连接,而建立连接需要一个时间,因此这是一个带启动时间的N -策略休假排队模型。
3.由于具有广阔的应用前景,近年来无线传感器网得到了广泛的关注。
在无线传感器网中,能量效率是无线传感器网设计需要考虑的一个重要性能指标。
数据块的传输是由源节点传向目的节点的,节点有两种状态,休眠状态和激活状态,当无数据块传输时其处于休眠状态,此时无能耗,当有数据块传输时处于激活状态,此时有能耗。
当有数据块到达需要传输时,节点由休眠状态转向激活状态,此时需要一个激活时间,并有一个相对大的能耗。
为了降低能耗,即减少节点转换次数,当节点处于休眠状态时,当数据块数量达到某个值N 时,节点才从休眠状态转向激活状态,直到无数据块传输时再次转向休眠。
因此这也是一个带启动时间的N -策略休假排队模型。
参考文献:
[1]田乃硕.休假随机服务系统[M ].北京:北京大学出版社,2001.
[2]唐应辉,唐小我.排队论基础与应用[M ].成都:电子科技大学出版社,2000.
[3]王铁英,韦才敏.带启动时间单重休假的M/G/1排队[J ].上海第二工业大学学报,2004,(1):14118
[4]王建军,杨德礼.带启动—关闭期的多重休假M/G/1排队[J ].燕山大学学报,2005,29(1):81121
[5]孟玉珂.排队论基础及应用[M ].上海:同济大学出版社,1989.
[6]卢锡城.A T M 网络原理和应用[M ].北京:电子工业出版社,1999.
[7]郭金淮,于宏毅,徐晓建.基于排队模型的无线传感器网性能研究[J ].计算机工程与应用,2006,08:20122.
8
8 申玉红:带启动时间的N -策略M/G/1排队 。
