反力计算
工程中常见静定结构的支座反力计算(工程力学课件)

之矩的代数和
最常用的应用形式
Fy
F
o
l
Fx
求力矩的两种方法
(1)定义
MO(F) F d
F
o
l
d
(2)合力矩定理
M O (F ) M O (Fx ) M O (Fy )
Fy
F
o
l
Fx
【例 1 】 解: (1)直接按定义 (2)按合力矩定理
【例 2】 求土压力使挡土墙倾覆的力矩?
(求力FR对A点的力矩)
力偶的表示符号
M F d
力偶的等效性
只要保持M不变,可任意改变F和d的大小 只要保持力偶矩M不变,力偶可在其作用面内任意移动和转动
力偶的性质
力偶在任一轴上的投影的代数和恒等于零 力偶对其作用面内任一点之矩恒等于力偶矩
y
o
F O
x
F’
MO (F ) MO (F ) F (x d ) F x Fd
F4x F4 cos 45 250 cos 45 176.78 (N)
F4
y
F4 sin 45 250 sin 45 176.78
(N)
平面汇交力系的平衡
y
FR F 0
Fx 0
Fy 0
x
平衡方程
【例 2】
平面三角支架,F=100kN, 求AB、AC杆的受力?
都是二力构件 的物体系统
FA
Fx Fy
0 0
MFx Fy
O00 0
MO 0
FBx FBy
平面力系平衡计算总结
平面 力系
平面汇交力系 平面
基本力系
平面力偶系
平面 特殊力系
平面平行力系
平面一般力系
排汽反力计算

m mm mm mm
0.6 6.2156 0.0259 3.3311 5 0.25 0.45
λ ξ 1
汽水管规P262公式6.1.3-4 λ / Di × L
(2)90 热压弯头阻力系数 90o热压弯头数 n2 90 热压弯头阻力系数 裤衩管阻力系数 (3)总阻力系数 总阻力系数 三 流态判别 质量流速 临界压力 Pc<Pa 四 求末端参数 管道末端压力 管道末端比容 P2 ν 2 b c ν 五 迭代法求比容比 介质比容比 总阻力系数 β ξ
第 1 页
排汽反力计算
一、辅助蒸汽联箱安全阀排汽管道排汽反力计算
序号 一 原始数据 当地大气压 排汽流量 滞止初压 排汽温度 滞止比容 滞止初焓 绝热指数 斜切角 气流偏转角 Pa G Po Ti ν I k θ φ
0 0
项目
符号
计算公式或依据
数据 0.1 20
单位 MPa t/h 106Pa ℃ m3/kg KJ/kg 度 度
2 o
ξ 2 ξ 3 ξ m Pc ξ 1 + n2× 2 +ξ 3 ξ 0.3537× G/Di2 (m/k)[(2kPoν 0)/(k+1)]0.5 汽水管规P43公式6.3.3-1 管内介质为亚临界流动状态 P2=Pa ν
2 2
5.0311 165.091 0.0733 kg /(s.m2) MPa
2
β *P2+(k-1)*(β -1/β )Pd2/k 汽水管规P45公式6.3.4-5 ν 2/β G/3.6 G1× 1 ν 3.1416× /4 Di Q/A1 G1× 1+(P1-Pa)× 1 ω A 汽水管规P61公式7.3.5-1 Fi*K(K=1.2) G/3.6 G2× 2 ν 2 3.1416× /4 Di Q/A2 G2× 2+(P2-2*Pa)*A2 ω 汽水管规P63公式7.3.5-8 Fi*cos(φ +θ )*K(K=1.2)
支座反力的计算反力怎么计算

支座反力计算简单的静定结构可以通过力的平衡与力矩的平衡来建立两个方程式,每个方程就是可以求一个未知量,就就是说,简单的静定结构只能求两个未知力;对于超静定结构计算就复杂了,不过还就是要用到平衡与力矩的平衡来建立方程,此外根据具体的情况增加其她方程联合求解,就就是说,有多少个未知力就需要多少个方程式;例如:一条简支梁长为L,两头AB简支,从左到右在1/3L处有个P向下的集中力,求两端支座反力。
这就就是简单的静定结构,解题如下:设两端的支座反力分别为:Ra与Rb根据垂直方向力的平衡条件得:Ra + Rb = P根据垂直方向力矩的平衡条件,以A为原点,得:Rb*L=P*1/3L(顺时针力矩等于逆时针力矩,A的支座反力过原点,力矩为零)联立两个方程组解得:Ra =2/3PRb =1/3P图解在这里就是用不上,所有结构力学的书都有计算的方法的,最好就就是找来瞧瞧,比我们在这里费尽心思的讲解要好得多。
例题: 简支梁的支座反力计算杆件长5米,离A端头1、5米有集中荷载为100N,问A,B两支座的反力为多少最佳答案RA=70KN RB=30KN1.1.5支座反力计算在静定结构的受力分析中,通常须预先求出支座反力,再进行内力计算。
求支座反力时,首先应根据支座的性质定出支座反力(包括个数与方位),然后假定支座反力的方向,再由整体或局部的平衡条件确定其数值与实际指向。
以图1-6a所示多跨刚架为例,讨论支座反力计算。
图1-6此刚架有五个支座反力:、、、与。
由整体的三个平衡方程,加上铰D与铰C处弯矩分别为零的平衡条件,即可求出这五个支座反力。
从几何组成的角度瞧,D 以右部分为三铰刚架,就是基本部分;D以左部分就是支承在地基与三铰刚架上的附属部分。
首先,取附属部分为隔离体(图1-6b),由平衡方程求、与。
(a)然后,将D铰处的约束反力反向加在基本部分上,取D以右三铰刚架为隔离体(图1-6c),利用平衡方程求与。
(b)(c)再取C以右半刚架为隔离体(图1-6d),由铰C处弯矩为零的平衡方程求。
支座反力计算公式详解

支座反力计算公式详解以支座反力计算公式详解为标题的文章如下:支座反力是工程力学中一个重要的概念,用于描述支座对物体的支撑力。
在工程设计和结构分析中,准确计算支座反力是确保结构安全和稳定的关键步骤。
本文将详细解释支座反力的计算公式及其应用。
支座反力的计算公式主要包括平衡方程和力矩方程。
平衡方程是基本的力学原理,它表明一个物体处于静力平衡状态时,所有作用在物体上的力的合力和合力矩都为零。
在支座反力计算中,我们通常将物体的平衡方程分为水平方向和垂直方向两个方程。
对于水平方向的平衡方程,我们可以使用以下公式进行计算:∑Fx = 0这个公式表示水平方向上所有作用在物体上的力的合力为零。
我们需要将物体上的所有水平力相加,包括外力和支座反力。
一般来说,水平方向上的外力主要包括水平方向的施加力和摩擦力。
通过平衡方程,我们可以计算出支座反力在水平方向上的分量。
对于垂直方向的平衡方程,我们可以使用以下公式进行计算:∑Fy = 0这个公式表示垂直方向上所有作用在物体上的力的合力为零。
和水平方向类似,我们需要将物体上的所有垂直力相加,包括外力和支座反力。
垂直方向上的外力主要包括物体的重力和其他施加力。
通过平衡方程,我们可以计算出支座反力在垂直方向上的分量。
除了平衡方程,力矩方程也是计算支座反力的重要工具。
力矩是一个力绕某一点旋转的趋势,可以用来描述物体受力情况。
在支座反力计算中,我们通常选择一个合适的点作为参考点,计算物体受力的力矩。
根据力矩方程,我们可以计算出支座反力在参考点处的力矩和力的大小。
支座反力计算公式主要包括平衡方程和力矩方程。
通过这些公式,我们可以根据物体受力情况,准确计算出支座反力的大小和方向。
这对于工程设计和结构分析非常重要,可以确保结构的安全和稳定。
在实际应用中,支座反力的计算需要考虑多种因素,例如物体的形状、力的大小和方向、支座的类型等。
在进行计算时,我们需要仔细分析和理解物体的受力情况,并根据具体情况选择合适的计算方法和公式。
支护结构反力计算方法

y
eaH
150.6 0.69m
γ(KP Ka ) 217.9
(三)绘制基坑支护简图
图3-33 基坑支护简图
图3-34 连续梁计算简图
(四)求各支点的荷载集度(没有考虑c!)
qA
=
qKa=
10×0.33 ___
=
3.3kN/m2
qB = qKa + γ AB Ka 3.3 + 19×5×0.33=34.6kN/m2
(九)反力核算
土压力及地面荷载共计: 3.3×23.5 + (150.6-3.3)×23.5/2 + 150.6× 0.69/2 = 1860.4kN 支点反力共计: RB+RC+RD+RF = 1938.8kN 误差: (1938.8-1860.4)/1860.4 = 4.2%
(十)H型钢的插入深度计算
fA
(11q1 4q2 )l 4 120EI
=16.4mm
图3-39 桩顶变形计算简图
因H型钢桩中心距为1.1m ,故须乘1.1 ,同时考虑土体变 形乘以3,桩顶变形为 16.4×1.1×3 = 54mm
3.6.2 二分之一分担法
• 二分之一分担法是多支撑连续梁的一种简化计算方法, 计算较为简便。
• Terzaghi和Peck根据对柏林和芝加哥等地铁工程基坑挡 土结构支撑受力的测定,以包络图为基础,用二分之一 分担法将支撑轴力转化为土压力,提出了图3-12所示的 土压力分布。反之,如土压力分布已知(设计计算时必 须确定土压力分布),则可以用二分之一分担法来计算 多道支撑的受力。这种方法不考虑支撑桩、墙的变形, 求支撑所受的反力时,直接将土压力、水压力平均分配 给每一道支撑,然后求出正负弯矩、最大弯矩,以确定 挡土桩的截面及配筋。显然,这种计算简单方便。计算 简图如图3-40所示。
静定结构的反力计算

⒊ 外伸梁:梁的一端或两端伸出支座的简支梁
【例2-4】图示伸臂梁受集中荷 载P=2kN, 三角形分布荷载q=1kN/m 作用。如果不计梁的自重, 试计算支 座A和B的反力。
解: ⑴取梁CD为研究对象
⑵列平衡方程求支座反力
X 0 : X A 0
MA 0 :P1
1 q3 2
1 RB 2 0
解: 取刚架为研究对象, 并取坐标 系如图所示。
X 0: X A P q 6 0 XA 34kN
M A 0 :
YB 6 m Q3 P 4 q63 0
YB
m
3Q
4P 6
18q
2 60 40 72 6
29kN
XA 34kN, YB 29kN
X A YA
YB
2.2.4 静定平面刚架反力计算
计算无误!
XA 34kN, YB 29kN
X A YA
YB
2.2.5 起重设备的验算
【例2-6】图示塔式起重机, 已知 规矩b=4m, 机身重G=260kN, 其作用 线到右侧的距离e=1.5m, 起重机平衡 重Q=80kN, 其作用线到左侧的距离 a=6m, 荷载P的作用线到右轨的距离 l=12m。
mA
Y
0:
YA
q
l 2
P sin
0
XA
YA
q
l 2
P sin
11.07kN
YA
M A 0 :
mA
q
l 2
3l 4
P cos
l
40.28kN m
⑶校核
MB 0 :
mA
q
l 2
l 4
YA
l
0
?
多跨连续梁支座反力计算

多跨连续梁支座反力计算多跨连续梁是现代桥梁结构中一种非常常见的形式,它在跨度和长度方面都具备了较大的优越性,承载能力和经济性均较为突出。
而在设计这样的结构时,支座反力的计算是一个至关重要的环节,在本文中,我们将给大家详细介绍一下多跨连续梁支座反力计算的各个步骤。
第一步:确定梁的几何形状和建模在计算支座反力之前,需要先了解梁的几何形状,包括梁的跨度、受载长度、断面性质、钢材性质等。
然后,将这些信息用计算机建模的方式呈现出来,便于后续的有限元分析。
第二步:进行静力计算在建立好模型之后,就可以进行静力计算,并根据梁在各种受力情况下的运动状态,得出支座反力。
在静力计算过程中,需要考虑到来自上游和下游的外力以及其他特殊负荷因素。
第三步:加入荷载计算进行完静力计算之后,接下来就需要加入不同种类的荷载进行计算了。
常见的荷载包括车辆荷载、温度荷载、风荷载等。
不同的荷载对支座反力的计算产生不同的影响,因此需要十分仔细地进行计算。
第四步:加入变形计算在梁受到荷载后,一定会发生变形,在支座反力的计算过程中,需要考虑到梁的变形。
变形通过不同的应变附加到梁的截面上,并进行计算,在这个过程中,需要考虑到混凝土的弹性模量、梁材料的弹性和塑性特性、预处理等。
第五步:重复计算前面的计算是建立在假设荷载稳定的情况下进行的。
实际上,荷载的突然变化会引起支座反力发生变化,因此,需要重复进行计算,并根据需要进行调整,保证计算结果的准确性。
以上,就是多跨连续梁支座反力计算的整个过程。
虽然这里仅仅提了一个粗略的概要,但是这一过程的计算是复杂而又十分耗费时间的,需要进行多方面的考虑。
在实际应用中,支座反力的计算是设计师需要反复攻坚克难的难点之一,需要进行多次的验证和检验,以保证梁的安全性和稳定性。
空心板桥梁板反力计算
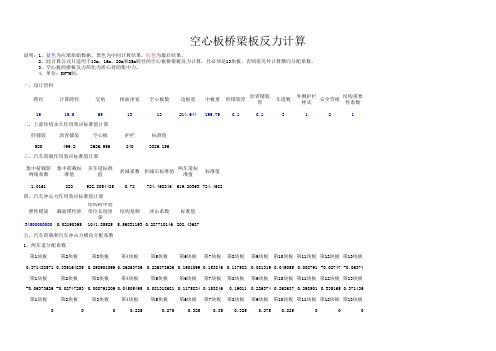
说明:1,蓝色为应填原始数据,黑色为中间计算结果,红色为最后结果。 2,此计算公式只适用于13m、16m、20m和25m跨径的空心板桥梁板反力计算,且必须是13块板,否则需另外计算横向分配系数。 3,空心板的梁板反力简化为质心处的集中力。 4,单位:KN-M制。
一,设计资料
跨径
计算跨径
第2块板
第3块板 第4块板 第5块板 第6块板 第7块板 第8块板 第9块板 第10块板 第11块板 第12块板 第13块板
125.5833803 116.6131389 107.6428974 98.672656 89.70241452 80.732173 71.76193 62.79169 53.82145 44.85121 35.88097 26.91072 17.94048
五,汽车荷载和汽车冲击力横向分配系数
1,两车道分配系数
第1块板
第2块板
第3块板 第4块板 第5块板 第6块板 第7块板 第8块板 第9块板 第10块板 第11块板 第12块板 第13块板
0.371428571 0.335164835 0.298901099 0.26263736 0.226373626 0.1901099 0.153846 0.117582 0.081319 0.045055 0.008791 -0.02747 -0.06374
第1块板
第2块板
第3块板 第4块板 第5块板 第6块板 第7块板 第8块板 第9块板 第10块板 第11块板 第12块板 第13块板
0.315
0.2925
第1块板
第2块板
0.045
0.0675
第1块板
第2块板
0
0
六,梁板反力
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B 类
A 为围护构件的从属面积A 11.7=m 2
μs1:风荷载局部体型系数
μs1(1):从属面积不大于1m 2时的体型系数,取
μs1(1) 1.4
:=μs1(25):从属面积大于或等于25m 2时的体型系数μs1(25)0.8μs1(1):=μs1(A):从属面积大于1m 2小于25m 2时的体型系数μz : 风压高度变化系数μz 1= βgz :高度z 处的阵风系数βgz 1.7
= Wk : 风荷载标准值(KN/m 2)Wk βgz μz ⋅μs1⋅W0⋅:=一、幕墙立柱的设计计算(反力提取)
幕墙立柱按简支梁力学模型进行设计计算:
1、结构尺寸
跨度(高度)L 6500mm :=左右面板宽度:B11800mm :=B21800mm :=荷载有效宽度:
2、荷载线分布最大荷载集度设计算(矩形分布)
(1)垂直于玻璃平面的风荷载作用
计算标高(m)z 6.5:= m 基本风压: W00.8KN m 2
-⋅:=地面粗糙度类别:
αmax 0.08
:=qEAK
: 垂直于玻璃幕墙平面的分布水平地震作用 (kN/m 2)
qEAK βE αmax ⋅GAK
⋅:=qEAK 0.361KN m
2
-⋅=qEK : 垂直于玻璃平面的分布水平地震作用线荷载标准值(kN/m)
qEK qEAK a
⋅:=qEK 0.65KN m 1
-⋅=γE : 地震作用分项系数
γE 1.3
:=qE : 地震荷载线分布最大荷载集度设计值(kN/m)
qE γE qEK
⋅:=qE 0.844KN m
1
-⋅=(4)荷载组合
q : 玻璃所受组合线荷载设计值:(kN/m)
采用SW+0.5SE 组合: (JGJ102-2003 5.4.2)
q qw 0.5qE
+:=q 5.174KN m
1
-⋅=3、结构分析
最大弯矩:
Mh 2.732107
⨯N mm
⋅=最大剪力:
Q 0.5q L
⋅:=Q 1.681104
⨯N
=立柱两端支座反力:
R Q
:=4、选用立柱型材的截面特性
γw : 风荷载作用效应的分项系数
γw 1.4
:=qwk : 风荷载线分布最大荷载集度标准值(kN/m)
qwk Wk a1a2+()
⋅:=qwk 3.394N mm
1
-⋅=qw : 风荷载线分布最大荷载集度设计值(kN/m)
qw γw qwk
⋅:=qw 4.751N mm
1
-⋅=(2)幕墙自重荷载
ρg :玻璃重度(KN/m 2)ρg 25.6KN m 3
-⋅:=t :玻璃厚度(mm )t 20mm :=ρg :立柱型材重度(KN/m 2)
ρa 78.5KN m 3-⋅:=Aa :立柱总截面面积(包括副框或扣盖)
Aa 6600mm
2:=Gk :幕墙自重(包括玻璃和框料)产生的轴向荷载(N )
Gk ρg t a ⋅()⋅120%+()⋅L ⋅ρa Aa ⋅L
⋅+:=Gk 10556.1N
=GAK :幕墙构件(包括玻璃和框料)的平均自重(KN/m 2)
GAK 0.902KN m
2
-⋅=βE :动力放大系数
βE 5:=αmax : 水平地震影响系数最大值
立柱刚度可以满足!
<
Umax 25.573mm
=
Umax : 立柱最大挠度校核依据: Umax ≤L/250 (JGJ102-2003 6.3.10)
6、幕墙立柱的刚度计算
立柱强度可以满足!
fb_a 205N mm
2
-⋅=<
强度校核:
F γ
G Gk
⋅:=F : 立柱轴向受力设计值(N )rG : 结构自重分项系数γG 1.2
:=γ 1.05:=γ: 塑性发展系数 校核依据: F/A+M/g/W ≤fa=215N/mm 2(拉弯构件)
5、幕墙立柱的强度计算
fv_a 120N mm
2
-⋅:=fc_a 205N mm
2
-⋅:=fb_a 205N mm
2
-⋅:=许用应力:
Ea 206000N mm
2
-⋅:=Aa 6600mm
2:=Ixa 1497.37cm
4:=Wxa 181.5cm 3
:=钢型材截面性质:40x165实心钢。
