重要极限的证明_1
两个重要极限的证明

两个重要的极限1.证明:0sin lim 1x x x→= 证明:如图(a )作单位圆。
当0<x<2π时,显然有ΔOAD 面积<扇形OAD 面积<ΔOAB 面积。
即111sin 222x x <<tgx ,sinx<x<tgx 。
除以sinx ,得到11sin cos x x x<< 或sin 1cos x x x >>。
(1) 由偶函数性质,上式对02x π-<<时也成立。
故(1)式对一切满足不等式0||2x π<<的x 都成立。
由0lim x →cosx=1及函数极限的迫敛性定理立刻可得0lim x →sin 1x x=。
函数f(x)=sin x x的图象如图(b )所示。
2.证明:1lim(1)n n n →∞+存在。
证明:先建立一个不等式,设b>a>0,于是对任一自然数n 有 11(1)n n n b a n b b a++-<+-或11(1)()n n n b a n b b a ++-<+-,整理后得不等式1[(1)]n n a b n a nb +>+-。
(1) 令a=1+11n +,b=1+1n ,将它们代入(1)。
由于11(1)(1)(1)(1)11n a nb n n n n +-=++-+=+, 故有111(1)(1)1n n n n ++>++,这就是说1{(1)}n n+为递增数列。
再令a=1,b=1+12n代入(1)。
由于11(1)(1)(1)22n a nb n n n +-=+-+=,故有111(1)22n n >+,12(1)2n n >+。
不等式两端平方后有214(1)2n n >+,它对一切自然数n 成立。
联系数列的单调性,由此又推得数列1{(1)}n n +是有界的。
于是由单调有界定理知道极限1lim(1)n n n→∞+是存在的。
重要极限的证明

1.求证:sin(π/(2n+1))sin(2π/(2n+1))sin(3π/(2n+1))……sin(nπ/(2n+1))=√(2n +1)/2^n,Sol:复数方法:复数方程 z^(2n+1)=1的根是 a1,a2,a3,...,a(2n),1。
其中,ak=cos(2kπ/(2n+1))+i sin(2kπ/(2n+1)),k=1,2,...,2n。
所以,ak=(a1)^k所以,z^(2n+1)-1=(z-a1)(z-a2)...(z-a(2n))(z-1),即(z-a1)(z-a2)...(z-a(2n))=(z^(2n+1)-1)/(z-1)=z^(2n)+z^(2n-1)+...+z+1。
两边令z=1,并取模,则:|1-a1|×|1-a2|×......×|1-a2n|=2n+1.........(*)因为,|1-ak|=√|(cos(2kπ/(2n+1))-1))+i sin(2kπ/(2n+1))|=2×sin(kπ/(2n+1)),所以由(*)式得:2^n×sin(π/(2n+1))sin(2π/(2n+1))sin(3π/(2n+1))……sin(nπ/(2n+1))=2n+1。
所以,sin(π/(2n+1))sin(2π/(2n+1))sin(3π/(2n+1))……sin(nπ/(2n+1))=√(2n+1)/2^n2.三角函数求证:sin(π/(2n+1))sin(2π/(2n+1))sin(3π/(2n+1))……sin(nπ/(2n+1))=√(2n +1)/2^n.证:sin(π/(2n+1))sin(2π/(2n+1))sin(3π/(2n+1))........sin(nπ/(2n+1))=√(2n +1)/2^n设Z=cos2π/(2n+1)+ isin2π/(2n+1)则x^(2n+1)=1的根为1,z,...z^2n得x^2n+...+x+1=(x-z)(x-z^2)...(x-z^2n)2n+1=|(1-z)||(1-z^2)|...|(1-z^2n)| (1)又|(1-z^k)|=2sinkπ/(2n+1) (2)|1-z^k| = |1-(cos(2kπ/(2n+1)) +sin(2kπ/(2n+1)) )|=|1-cos(2kπ/(2n+1))) -sin(2kπ/(2n+1)) )|=√((1-2cos(2kπ/(2n+1)) +cos^2 (2kπ/(2n+1))) + sin^2 (2kπ/(2n+1))) =√(2-2cos(2kπ/(2n+1)) )=√(4sin^2(kπ/(2n+1))=2sin(kπ/(2n+1)故2n+1 =( n(π/(2n+1)). n(2π/(2n+1)) n(3π/(2n+1))........ n(2nπ/(2n+1)) 两边开方,得sin(π/(2n+1))sin(2π/(2n+1))sin(3π/(2n+1))........sin(nπ/(2n+1)) =√(2n+1) / 2^n另外那个类似,可以尝试自己证一下.3.为什么sinπ/n+sin2π/n......+sin(n-1)π/n=cotπ/2n?解:2 sin [π/(2n)]·sin(π/n)= cos [π/n -π/(2n)]- cos [π/n +π/(2n)]= cos [π/(2n)]- cos [3π/(2n)]2 sin [π/(2n)]·sin(2π/n)= cos [2π/n -π/(2n)]- cos [2π/n+π/(2n)]= cos [3π/(2n)]- cos[5π/(2n)]2 sin [π/(2n)]·sin(3π/n)= cos [3π/n -π/(2n)]- co s [3π/n +π/(2n)]= cos [5π/(2n)]- cos [7π/(2n)]……2 sin [π/(2n)]·sin[(n-1)π/n]= cos [(n-1)π/n -π/(2n)]- cos [(n-1)π/n +π/(2n)]= cos [(2n-3)π/(2n)]- cos [(2n-1)π/(2n)]故:2 sin [π/(2n)] ·{sin(π/n)+sin(2π/n)+......+sin[(n-1)π/n]}= cos [π/(2n)]- cos [(2n-1)π/(2n)]= cos [π/(2n)]- cos [π-π/(2n)]=2 cos [π/(2n)]故:sin(π/n)+sin(2π/n)+......+sin[(n-1)π/n]= cos[π/(2n)]/ sin[π/(2n)]= cot [π/(2n)]4.级数sin n/(n+1)收敛还是发散,如果收敛,是绝对收敛还是条件收敛,为什么? Sol:收敛,Dirichlet 判别法.这是最典型的一个用Dirichlet 判别法判别收敛的例子.sinn 的部分和=[sin1/2(sin1+sin2+...+sinn)]/sin1/2(积化和差公式)=[cos1/2-cos(2n+1)/2)]/sin1/2,于是有界,1/(n+1)单调递减趋于0,收敛.不绝对收敛.|sinn/(n+1)|>=sin^2n/(n+1)=[1-cos(2n)]/2(n+1).类似用Dirichl et 判别法知道级数cos2n/(n+1)收敛,但级数1/(n+1)发散,于是易知不绝对收敛.建议记住这个典型例子.12122ln ln ...ln lim .2ln ln ln ...ln n ln 2ln 1:ln 2ln =ln 2o n n n n x no n n n n c c c I nn c c c n n sol n n n n nI →∞+++=+++-≤==-求5.求sin π/n*sin2π/n*…*sin(n-1)π/n 的值,用复数思想6.三角函数连乘(正弦)求证:sin[π/(2n+1)]*sin[2π/(2n+1)]*sin[3π/(2n+1)]*……*sin[nπ/(2n+1)]=(根号下2n-1)/2^nSol:7.证一般项级数∑sin√(n^2+1)π条件收敛Sol:∵sin√(n²+1)π=[(-1)^n]sin[√(n²+1)π-nπ]=[(-1)^n]sin[√(n²+1)-n]π=[(-1)^n]sin{1/[√(n²+1)+n]}πlim(n→∞)[sin{1/[√(n²+1)+n]}π]/(1/n)=lim(n→∞)nπ/[√(n²+1)+n]=π/2∴∑sin{1/[√(n²+1)+n]}与∑1/n有相同的敛散性,即∑sin{1/[√(n²+1)+n]}π发散lim(n→∞)sin{1/[√(n²+1)+n]}π=0,且sin{1/[√[(n+1)²+1]+(n+1)]}π≤sin{1/[√(n ²+1)+n]}π由莱布尼兹判别法知lim[(-1)^n]sin{1/[√(n²+1)+n]}π收敛∴原级数条件收敛其他回答:sin√(n^2+1)π=(-1)^n sin(√(n^2+1)π+nπ)再利用分子有理化可得:(-1)^n sin(π/[根号(n^2+1)+n])利用 Dirichlet判别法可知级数收敛。
极限存在准则 两个重要极限

y 2.594 2.705 2.7169 2.71815 2.71827 …
x -10 -100 -1000 -10000
y 2.88 2.732 2.720
2.7183
y
1
1 x
x
的值无限接近于一个常数
-100000 … 2.71828 …
e 2.718281828459045
xn
a xn
a
xn1 xn
1(1 2
a xn2
)
1 2
(1
a) a
1
∴数列单调递减有下界,
故极限存在,
设
lim
n
xn
A
则由递推公式有 A 1 ( A a ) 2A
A a
x1 0,
xn 0, 故
lim
n
xn
a
三、 两个重要极限
证: 当
x(0,
则
a 2a
lim
n
xn
lim
n
2 xn1
a2 2 a
a2 a 2 0
a2
备用题
1.设
xn1
1 2 ( xn
a xn
)(
n
1
,
2
,
) , 且 x1 0 ,
a0, 求
lim
n
xn
.
利用极限存在准则
解:
1
a
xn1 2 ( xn xn )
令z=1/x, 则x→∞时, z→0,
由此可得:
1
1
lim(1 z)z lim(1 x)x = e
两个重要极限的证明

两个重要的极限1.证明:0sin lim 1x x x→= 证明:如图(a )作单位圆。
当0<x<2π时,显然有ΔOAD 面积<扇形OAD 面积<ΔOAB 面积。
即111sin 222x x <<tgx ,sinx<x<tgx 。
除以sinx ,得到11sin cos x x x<< 或sin 1cos x x x >>。
(1) 由偶函数性质,上式对02x π-<<时也成立。
故(1)式对一切满足不等式0||2x π<<的x 都成立。
由0lim x →cosx=1及函数极限的迫敛性定理立刻可得0lim x →sin 1x x=。
函数f(x)=sin x x的图象如图(b )所示。
2.证明:1lim(1)n n n →∞+存在。
证明:先建立一个不等式,设b>a>0,于是对任一自然数n 有 11(1)n n n b a n b b a++-<+-或11(1)()n n n b a n b b a ++-<+-,整理后得不等式1[(1)]n n a b n a nb +>+-。
(1) 令a=1+11n +,b=1+1n ,将它们代入(1)。
由于11(1)(1)(1)(1)11n a nb n n n n +-=++-+=+, 故有111(1)(1)1n n n n ++>++,这就是说1{(1)}n n+为递增数列。
再令a=1,b=1+12n代入(1)。
由于11(1)(1)(1)22n a nb n n n +-=+-+=,故有111(1)22n n >+,12(1)2n n >+。
不等式两端平方后有214(1)2n n >+,它对一切自然数n 成立。
联系数列的单调性,由此又推得数列1{(1)}n n +是有界的。
于是由单调有界定理知道极限1lim(1)n n n→∞+是存在的。
两个重要极限的证明

两个重要极限的证明嘿,小伙伴们!咱们今天来聊聊两个超级重要的极限。
这两个极限在数学里可有着举足轻重的地位呢!第一个重要极限是:当 x 趋近于 0 时,lim(sin x / x) = 1 。
第二个重要极限是:当 x 趋近于无穷大时,lim(1 + 1/x)^x =e 。
第一个重要极限的证明咱们先来看第一个重要极限的证明哈。
我们知道,单位圆中,角 x 对应的弧长是 x ,而对应的弦长是2sin(x/2) 。
因为弧长大于弦长,所以 x > 2sin(x/2) ,即 sin(x/2) x/2 。
同时,根据三角形的面积关系,扇形的面积是 1/2 x ,三角形OAB 的面积是 1/2 tan x ,而扇形的面积大于三角形的面积,所以1/2 x > 1/2 tan x ,即 x tan x 。
所以 cos x sin x / x 1 ,当 x 趋近于 0 时,cos x 和 1的极限都是 1 ,根据夹逼准则,就可以证明 lim(sin x / x) = 1啦!第二个重要极限的证明看看第二个重要极限。
我们设 y = (1 + 1/x)^x ,对其取对数,得到 ln y = x ln(1 +1/x) 。
然后令 t = 1/x ,则 x = 1/t ,ln y = (1/t) ln(1 + t) 。
根据洛必达法则,对 (ln(1 + t))/t 求极限,当 t 趋近于 0 时,其极限为 1 。
所以当 x 趋近于无穷大时,ln y 的极限是 1 ,那么 y 的极限就是 e ,就证明了 lim(1 + 1/x)^x = e 。
怎么样,这两个重要极限的证明是不是很有趣呀!。
第一重要极限证明

第一重要极限证明极限是微积分中的重要概念之一,它在数学和科学中具有广泛的应用。
而第一重要极限证明则是极限理论中最基础的证明之一。
本文将从人类视角出发,详细描述第一重要极限的证明过程,使读者能够更好地理解并感受这一数学原理的美妙。
我们先来介绍一下第一重要极限的概念。
在微积分中,当自变量趋向于某个特定值时,函数的极限就是函数在该特定值附近的行为。
第一重要极限是指当自变量趋向于某个常数a时,函数f(x)的极限。
具体来说,如果对于任意给定的正数ε,存在一个正数δ,使得当0 < |x - a| < δ时,有|f(x) - L| < ε成立,那么我们就说函数f(x)在x趋近于a时的极限为L。
接下来,我们将通过一个实例来说明第一重要极限的证明过程。
考虑函数f(x) = 2x + 1,我们需要证明当x趋近于2时,函数f(x)的极限为5。
我们给定一个任意的正数ε,我们需要找到一个正数δ,使得当0 < |x - 2| < δ时,有|f(x) - 5| < ε成立。
我们可以先尝试通过代入一些近似值来判断可能的δ的取值范围。
当我们令x = 1.9时,可以得到f(1.9) = 2(1.9) + 1 = 3.8 + 1 = 4.8,而当x = 2.1时,可以得到f(2.1) = 2(2.1) + 1 = 4.2 + 1 = 5.2。
可以看出,当x在1.9和2.1之间时,f(x)的值在4.8和5.2之间变化。
根据这一观察,我们可以猜测当0 < |x - 2| < 0.1时,有|f(x) - 5| < 0.2成立。
接下来,我们需要证明这一猜测的正确性。
假设存在一个正数δ,使得当0 < |x - 2| < δ时,有|f(x) - 5| < 0.2成立。
我们可以取δ = 0.1,根据我们的猜测,这个δ是满足条件的。
现在,我们可以证明当0 < |x - 2| < 0.1时,有|f(x) - 5| < 0.2成立。
高等数学第3章第4节两个重要的极限
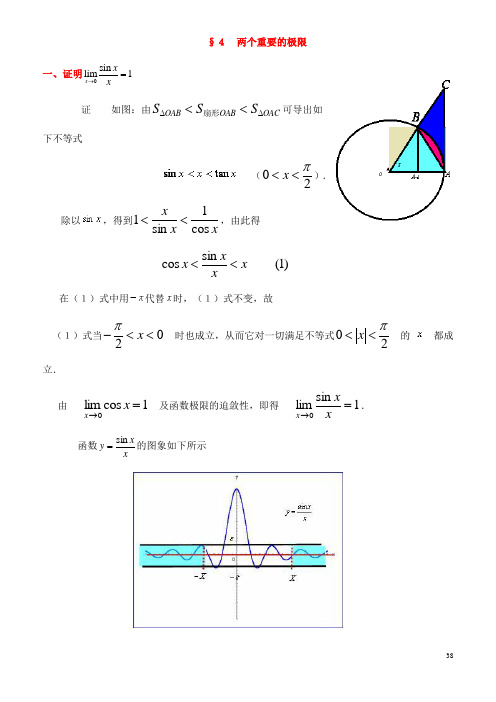
§4 两个重要的极限一、证明0sin lim 1x xx→=证 如图:由OAC OAB OAB S S S ∆∆<<扇形可导出如下不等式(20π<<x ).除以,得到x x x cos 1sin 1<<,由此得 )1(sin cos xxx x <<在(1)式中用代替时,(1)式不变,故(1)式当02<<-x π时也成立,从而它对一切满足不等式20π<<x 的 都成立.由1cos lim 0=→x x及函数极限的迫敛性,即得1sin lim 0=→xx x . 函数xxy sin =的图象如下所示例1.求sin limx xx ππ→-.例2.求201cos lim x xx →-.注:利用归结原则,可求数列极限。
如求1sin1limlim sin 1n n n n nn→∞→∞=,直接利用0sin lim 1x x x →=是不严格的;但已知0sin lim1x x x →=,故取,(1,2,)n x n n π== ,则0()n x n →→∞,从而由归结原则1sinlim ()lim01n n n n f x n →∞→∞==. 例3.求0lim x tgxx→.二、证明e xxx =+∞→)11(lim 或. e =+→ααα10)1(lim 证 所求证的极限等价于同时成立以下两个极限e xx x =++∞→)11(lim (2)e xx x =+-∞→)11(lim (3)先利用数列极限e nn n =+∞→)11(lim证明(2)式成立.为此,作定义在上),1[+∞的两个阶梯函数如下:nn x f )111()(++=,,1)11()(++=n nx g,,易见f 增(第二章§3习题4)且有上界,g 减(第二章§3习题9)且有下界.故据上节习题2,)(lim x f x +∞→与)(lim x g x +∞→皆存在.于是,由归结原则(取}{}{n x n =)得到e n xf nn x =++=∞→+∞→)111(lim )(lim e nx g n n x =+=+∞→+∞→1)11(lim )(lim 另一方面,当时有nx n 1111111+<+<++以及1)11()11()111(++<+<++n x n nx n,即有)()11()(x g xx f x<+<,),1[+∞∈x .从而根据迫敛性,定理(2)式得证. 现证(3)式.为此作代换y x-=,则y y x y y x )111()11()11(-+=-=+-,且当-∞→x 时+∞→y ,从而有e y y x yy y y x x =-+=-=++∞→-+∞→-∞→)111(lim )11(lim )11(lim 以后还常用到e 的另一种极限形式:e =+→αα1)1(lim(4)事实上,令x1=α,则0→⇔∞→αx ,所以e xxx =+=+→∞→ααα10)1(lim )11(lim例1.求()10lim 12xx x →+.例2.求()10lim 1xx x →-.例3.求211lim(1)nn n n →∞+-.作业:p58. 1(2), (5), (8), (9), (10) , 2(1), (3), (5), (6), 3.。
关于一个重要极限的两种证明方法

递 增有上界, 再根据单调有界定理 极限 l i m f l + 1 存在。 但实际 教学
中, 学 生往往感觉这样的证明 比较抽象 . 过程不简洁 . 难 以理解 。不少
, 盟
、
O  ̄ 1 +O r 2 ]
㈩ ቤተ መጻሕፍቲ ባይዱ
学 者对此进行 了研究。崔德旺I 3 ] 等利用几何均值不等式给 出了存在性 的一种简洁证法 杨华 1 从连续性和导数定 义的角度给 出了重要极限
n
[ A b s t r a c t ] T h i s p a P e r d i s c u s s e s t h e e x i s t e n e e o f i m p o r t a n l l i m i t l i m ( 】 1 ) = e . R e s p e c t i v e l y u s i n g t w o i n e q u a l i t i e s j n c o m b i n a t i 。 n w i t h m o H o t o n e
b o u n d e d t h e o r y , t wo c o n c i s e p r o o f i s g i v e n.
【 K e y w o r d s ] L i m i t ; P r o o f ; M o n o t o n e b o u n d e d t h e o y r
n
1
令 ( 4 ) 中 a : n 一 1 , n = l 。 = n , 口 : 1 , 则 ( L ) ( 芸 ), 即
的证明方法。本文给出对极限l f l + 1 存在性的两种简洁证法。
1 预 备知 识
引理 1 1 5 】 设实数 > 一 1 . 为正整数 . 则有
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重要极限的证明
重要极限的证明极限是ea0在n比较大时,(1 (1-a)/n)^n=原式=(1 1/n)^n取极限后,e》=原式的上极限》=原式的下极限》=e^(1-a)由a的任意性,得极限为e利用极限存在准则证明:(1)当x趋近于正无穷时,(Inx/x^2)的极限为0;(2)证明数列{Xn},其中a0,Xo0,Xn=[(Xn-1) (a/Xn-1)]/2,n=1,2,…收敛,并求其极限。
1)用夹逼准则:x大于1时,lnx0,x^20,故lnx/x^20且lnx1),lnx/x^2(x-1)/x^2.而(x-1)/x^2极限为0故(Inx/x^2)的极限为02)用单调有界数列收敛:分三种情况,x0=√a时,显然极限为√ax0√a时,Xn-X(n-1)=[-(Xn-1) (a/Xn-1)]/20,单调递减且Xn=[(Xn-1) (a/Xn-1)]/2√a,√a为数列下界,则极限存在.设数列极限为A,Xn和X(n-1)极限都为A.对原始两边求极限得A=[A (a/A)]/2.解得A=√a同理可求x0√a时,极限亦为√a综上,数列极限存在,且为√(一)时函数的极限:以时和为例引入.介绍符号: 的意义, 的直观意义.定义( 和. )几何意义介绍邻域其中为充分大的正数.然后用这些邻域语言介绍几何意义.例1验证例2验证例3验证证……(二)时函数的极限:由考虑时的极限引入.定义函数极限的“ ”定义.几何意义.用定义验证函数极限的基本思路.例4 验证例5 验证例6验证证由=为使需有为使需有于是, 倘限制, 就有例7验证例8验证( 类似有(三)单侧极限:1.定义:单侧极限的定义及记法.几何意义: 介绍半邻域然后介绍等的几何意义.例9验证证考虑使的2.单侧极限与双侧极限的关系:Th类似有: 例10证明: 极限不存在.例11设函数在点的某邻域内单调. 若存在, 则有= §2 函数极限的性质(3学时)教学目的:使学生掌握函数极限的基本性质。
教学要求:掌握函数极限的基本性质:唯一性、局部保号性、不等式性质以及有理运算性等。
教学重点:函数极限的性质及其计算。
教学难点:函数极限性质证明及其应用。
教学方法:讲练结合。
一、组织教学:我们引进了六种极限: , .以下以极限为例讨论性质. 均给出证明或简证.二、讲授新课:(一)函数极限的性质:以下性质均以定理形式给出.1.唯一性:2.局部有界性:3.局部保号性:4.单调性( 不等式性质):Th 4若和都存在, 且存在点的空心邻域,使,都有证设= ( 现证对有)註:若在Th 4的条件中, 改“ ”为“ ”, 未必就有以举例说明.5.迫敛性:6.四则运算性质:( 只证“ ”和“ ”)(二)利用极限性质求极限:已证明过以下几个极限:(注意前四个极限中极限就是函数值)这些极限可作为公式用. 在计算一些简单极限时, 有五组基本极限作为公式用,我们将陆续证明这些公式.利用极限性质,特别是运算性质求极限的原理是:通过有关性质, 把所求极限化为基本极限,代入基本极限的值, 即计算得所求极限.例1( 利用极限和)例2例3註:关于的有理分式当时的极限.例4 [ 利用公式]例5例6例7。
