11.3 格林公式

合集下载

11-3曲面解析

L AO ( x 2 3 y ) d x ( y 2 x) d y OA
( x 2 3 y ) d x ( y 2 x) d y
D
4 2 x dx 0
4 d xd y
64 8 3
y
L D
o
Ax
例 3 计算 L 2xydx x2dy 其中 L 为抛物线
1 1 ONA xdy ydx AMO xdy ydx 2 2
1 AMO xdy ydx 2
1 0 a a x( 1)dx ( ax x )dx 2 2 ax
a a 1 2 0 xdx 6 a . 4
M
A(a ,0)
N
三、平面上曲线积分与路径无关的条件
取 P y, Q x, 得 2
dxdy xdy ydx
L D
二、格林公式的应用
1.简化曲线积分
例 1 计算
AB
y
A
D
xdy,其中曲线
x
AB 是半径为 r 的圆在第一象限部分.
o
L
B
解
引入辅助曲线 L,
L OA AB BO 应用格林公式, P 0, Q x 有
第十一章曲线积分
第三节格林公式及其应用
一、格林公式
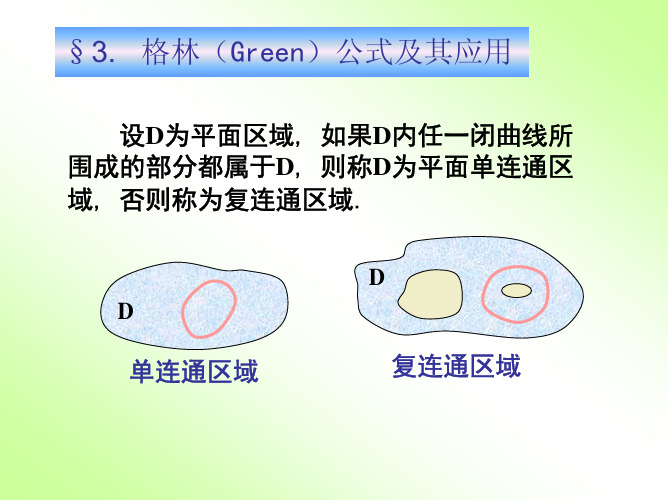
1.单复连通区域
定义：设D为平面区域如果D内任一闭曲线所围的部分都属于D 则称D为平面单连通区域否则称为复连通区域
D D
单连通区域
复连通区域
2.边界曲线的方向
定义：当观察者沿区域D的边界曲线L行走时如果左手在区
域D内则行走方向是L的正向
P Q ， y x 原积分与路径无关

格林公式

1 2 3
= ∫L Pdx + Qdy + ∫L Pdx + Qdy + ∫L Pdx + Qdy
1 2 3
= ∫L Pdx + Qdy
L3
D3
D2
L2
( L1, L2 , L3对D来说为正方向 )
D1
L1
L
证明(3)
若区域不止由一条闭曲线所围成.添加直线段 AB,CE. 则 D 的边界曲线由 AB, L2 ,BA, AFC,CE, L3 , EC 及 CGA 构成. D 由(2)知
o
L
B
x
解引入辅助曲线 L , L = OA + AB + BO
应用格林公式 ,
(
P = 0, Q = x 有
y
− ∫∫ dxdy = ∫ xdy
L D
A
D
= ∫OA xdy + ∫AB xdy + ∫BO xdy , 由于 ∫OA xdy = 0,
o
L
B
x
∫BO xdy = 0,
1 2 ∴ ∫ xdy = − ∫∫ dxdy = − πr . AB 4 D
∂P ∂ 2u ⇒ = ∂y ∂x∂y
=
∂ u ∂Q = ∂y∂x ∂x
2
(4) ⇒ (1) :
（1）对 D内任意一条闭路径 L, ∫ Pdx + Qdy = 0;
L
∂Q ∂P (4) = , ∀( x , y ) ∈ D . ∂x ∂y
D′
L D
设 L 是 D 内一条闭路径， L 所围有界闭区域 D ′ ⊂ D , 则在 D ′内 ∂ Q = ∂ P , ∂x ∂y

§11.3 格林(Green)公式

y
下面证明如图，
A(x0 , y0 )
B(x,y) M(x+Dx,y)
O
G
x
2. 平面上曲线积分与路径无关的等价条件
类似可证
y
A(x0 , y0 )
B(x,y) M(x+Dx,y)
O
G
x
( ξ 介于 x 与 x +Dx 之间 )
2. 平面上曲线积分与路径无关的等价条件
如果存在某一函数 u (x, y) 使 du = Pdx + Qdy，则
(Ⅰ) 沿任一闭曲线L的积分
(Ⅱ) 曲线积分
与路径无关；
（Ⅲ）存在某一函数 u (x, y) 使 du = Pdx + Qdy；
（Ⅳ）在G内
证明略.
2. 平面上曲线积分与路径无关的等价条件
如果存在某一函数 u (x, y) 使 du = Pdx + Qdy，如何求 u (x, y)？
此时，积分与路径无关，只与起点和终点有关，如图，记
1. 区域的连通性
设 D 为平面区域，如果 D 内任一闭曲线所围成的部分都属于 D，则称 D 为平面单连通区域，否则称为复连通区域.
例 D1,D2为图中浅色区域.
D2 D1
单连通区域
复连通区域
1. 格林（Green）公式
L
D
L
Dl
边界曲线 L 的正向: 当观察者沿边界行走时，区域 D 总在他的左边。
§11.3 格林(Green)公式
1. 格林(Green)公式 2. 平面上曲线积分与路径无关的
等价条件 3. 曲线积分的基本定理
§11.3 格林(Green)公式
1. 格林(Green)公式 2. 平面上曲线积分与路径无关的

11.3格林公式

y
x
由定理2 可知, 存在函数 u (x , y) 使 du Pdx Qdy
u(x, y) xy2dx
1 x2 y2 2
C ( y)
又
所以
u(x, y)
则 1 x2 y2 C 2
例6.
验证
x
dy x2

y y
d
2
x
在右半平面
(
x
>
0
)
内存在原函
数 , 并求出它.
o (1,0) ( x,0) x
arctan x
注意! 2
y
例５-６求二元函数u(x,y)使du=P (x,y) dx+Q (x,y) dy
称为二元函数的全微分求积. 简单情况时可按下列方法求解
所以
全微分方程
1.定义: 若存在 u(x, y) 使, du P (x, y)dx Q(x, y)dy 则称 P (x, y) dx Q (x, y) dy 0 ①
例2. 设 L 是一条分段光滑的闭曲线, 证明
2xy dx x2 dy 0 L
证: 令 P 2xy, Q x2, 则
利用格林公式 , 得
2xy dx x2 dy L
0dx dy
0
D
例3. 计算
其中L为一无重点且不过原点
的分段光滑正向闭曲线. 解: 令
则当x2 y2 0时,
说明: 根据定理2 , 若在某区域内 P Q , 则 y x
1) 计算曲线积分时, 可选择方便的积分路径; 2) 求曲线积分时, 可利用格林公式简化计算,
若积分路径不是闭曲线, 可添加辅助线; 3) 可用积分法求d u = P dx + Q dy在域 D 内的原函数:

格林公式

∵ ∫ − ydx + xdy = ∫∫ [1 − ( −1)]dxdy = 2 ∫∫ dxdy ,
L
1 ∴ ∫ − y d x + x d y 是 L 所围区域 D 的面积 . 2 L 例1 求椭圆 x = a cos θ , y = b sin θ 所围成图形的面积 A . 1 解 A = ∫ − ydx + xdy 2L 1 2π = ∫ − b sin θ ⋅ d ( a cos θ ) + a cos θ ⋅ d ( b sin θ ) 2 0 2π 1 = ab ∫ dθ = πab. 7 2 0
∂Q ∂P ∵ = ∂x ∂y
y yd x − x d y , 其中 L 为圆课堂练习求 ∫ 2 2 L 2( x + y ) P214.3 周 ( x − 1 ) 2 + y 2 = 2 , L 的方向逆时针 . O l D 所围区域为解设 L所围区域为 D . y −x P( x, y) = , Q( x, y) = . 2 2 2 2 2( x + y ) 2( x + y ) x2 − y2 ∂P ∂Q ∵ = = 在 D 内不连续 , ( 0,0 )是奇点 . 2 2 2 ∂ y 2( x + y ) ∂x ∴ D 上不能用格林公式 (见 P 202 定理 1条件 ).
在 D 内作小圆周 l : x 2 + y 2 = r 2方向逆时针 (如图 ).
ydx − xdy 用P 205 第 8 −10 ∫ 2( x 2 + y 2 ) ======== 行的方法得 L
L
x
∫
( 小圆 )
l
y d x − x d y 曲线L上的积分可以化成同上的积分可以化成同上的积分. 2 ( x 2 + y 2 ) 方向的小圆周 l 上的积分.

高等数学：格林公式

D
由于 xdy 0,
xdy 0, xdy dxdy 1 r2.
OA
BO
AB D
4
2. 简化二重积分
y
例 2 计算
e y2 dxdy ,其中D 是
B 1
D
D
以O(0,0), A(1,1), B(0,1)为顶点
的三角形闭区域.
o
解令P 0, Q xe y2 ,
A
1
x
则 Q P e y2 , x y
c
1 ( y) x
d
c
Q(
2
(
y),
y)dy
d
c
Q(
1(
y),
y)dy
ห้องสมุดไป่ตู้
y
Q( x, y)dy Q( x, y)dy
CBE
CAE
d
x 1( y)
Q( x, y)dy Q( x, y)dy
CBE
EAC
A
c
LQ( x, y)dy
o
E D B
C
x 2( y)
x
同理可证
D
P y
dxdy
L
P(
A
1 2
L
xdy
ydx
1
2 ONA
xdy
ydx
1
2 AMO
xdy
ydx
1
2 AMO
xdy
ydx
M
N
A(a,0)
1 2
0
a
x(
2
a ax
1)dx
(
ax x)dx
a a
40
xdx 1 a2 . 6
例3. 计算

高等数学格林公式课件

他近处的部分总在他的
左边. 单连通区域的边界曲线L的正向: 逆时针方向.
设复连通区域 D 的边界曲线为 = L + l 1 + l2 + · · · + ln 的正向：复合闭路 (如图)
外边界L 为逆时针方向；内边界
li
( i 1, 2, , n)
为顺时针方向.
4. 格林公式定理10.3（Green公式）设平面区域 D 是由分段光滑闭曲线围成, 函数有连续一阶偏导数, 则
D
D
3 [1 ( x 2 y 2 )]d x d y
D
3 d (1 2 ) d
0 0
2π
R
3π ( 2 R 2 R4 ) 2
注 I 3 [1 ( x 2 y 2 )]d x d y
D
？ 3 (1 R 2 ) d x d y
y
A(1,1)
B(0,1)

D
Q P ( ) d xd y x y
D
P dx Qd y
D
yx
o
x
2 y ？
将二重积分转化为曲线积分

D

P dx Qd y
P ？ Q xe 0, Q
解令 P 0, Q xe 利用格林公式 , 有
y2
作位于 D 内圆周
l : x 2 y2 r 2,
顺时针.
l x
l的参数方程为： x r cos y r sin : 2 0
y L
O
记 D1 由 L 和 l 所围成的区域,
L l 封闭，正向 .
应用格林公式,得

格林公式

d ( y xy x3 x4 ) 0. 34
C 不定积分法: u x2 x3 y, x
( x2 x3 y)dx x3 x4 xy C( y),
34
u x C( y), 又 u 1 x,
y
y
x C( y) 1 x, C( y) 1, C( y) y, 原方程的通解为 y xy x3 x4 C .
L P( x, y)dx Q( x, y)dy 0.
证明: 由格林公式得
L
P(
x,
y)dx

Q(
x,
y)dy

D

Q x

P y
dxdy

0
其中D是L所围平面区域.
（4）对G内的任意一条分段光滑的闭曲线 L,
L P( x, y)dx Q( x, y)dy 0. (1) 曲线积分 L P( x, y)dx Q( x, y)dy 在G内与路径
无关.
证明: 在G内任取两点M0, M1, y 设L1和L2是G内从M0到M1的任意两条定向曲线, 现要证
Pdx Qdy Pdx Qdy
L1
L2
o
L1
M1
G
M0
L2
x
已知条件是什么?
Pdx Qdy 0
L1 L2
有关定理的说明： (1) 开区域 G 是一个单连通域.
(2) 函数P( x, y), Q( x, y)在 G 内具有一阶连
续偏导数.
两条件缺一不可以上四个等价命题最好用的是
曲线积分 L P( x, y)dx Q( x, y)dy在G内与路

格林公式

由格林公式得

C
Pdx

Qdy

D
(
Q x

P y
)d
0
定理2的应用
(1)求 Pdx Qdy
L
若积分与路径无关，可选取简单路径计算.

2
(
x
)
L

L3
L4
L1
L2
L3
L4
L1
L2
x
b
a

a P( x,1( x)) dx b P( x,2( x))dx b [P( x,1( x)) P( x,2( x))] dx
a
b
L1 y 1( x)
a P d P( x, y)dx
I

Q

D
(
x

P )d
y
0
P y
y2 x2 ( x2 y2 )2
Q x
(0,0) D 在D内不能用格林公式
在D内取一圆周l x2 y2 r 2 , r 0
记L及l所围成的复连通区域为D1
在D1 应用格林公式得
Ll
xdy x2
L1
（三）应用
Q

D
(
x

P )d
y

L
Pdx

Qdy
1.求 P( x, y)dx Q( x, y)dy
L
例1.(1)求 y4dx 4xy3dy，L : x2 y2 4, 取正向
解
L
设L所围闭区域D : x2 y2 4

高等数学课件--D11_3格林公式

2012-10-12
同济版高等数学课件
定理2 目录上页下页返回结束
证明 (2) (3) 在D内取定点与路径无关, 有函数
和任一点B( x, y ), 因曲线积分
B( x, y )
A( x0 , y0 )
( x x , y ) ( x, y )
C ( x x, y )
则
dy 1 y
2
O (1,0)
x y
( x,0 )
x

π 2
arctan
2012-10-12
同济版高等数学课件
目录上页下页返回结束
例7. 设质点在力场由 A( 0, ) 移动到
2 π
作用下沿曲线 L : 求力场所作的功W
y
k
L
A L
O
解: W F d s
L
r
( y dx x d y) 2
Q x P y
L
Dn

k 1 n
Dk

d xd y
O
x

k 1
Dk
P dx Qd y
(Dk 表示 Dk 的正向边界 )
证毕
P dx Qd y
L
2012-10-12
同济版高等数学课件
定理1 目录上页下页返回结束
Q P d xd y P d x Q d y 格林公式 x y D L
Pd x Qd y

L2
(1) 沿D 中任意光滑闭曲线 L , 有 L Pd x Qd y 0 说明: 积分与路径无关时, 曲线积分可记为 .
B (2) 对D 中任一分段光滑曲线 L, 曲线积分 L Pd x Qd y Pd x Qd y Pd x Qd y AB 与路径无关, 只与起止点有关. A

D11_3格林公式

第三节一、格林公式二、平面上曲线积分与路径无关的等价条件格林公式及其应用第十一章*三、全微分方程L D区域 D 分类单连通区域 ( 无“洞”区域 )多连通区域 ( 有“洞”区域 )域 D 边界L 的正向: 域的内部靠左定理1. 设区域 D 是由分段光滑正向曲线 L 围成,则有,),(y x P ),(y x Q ∫∫∫+=⎟⎠⎞⎜⎝⎛∂∂−∂∂LD y Q x P y x y P x Q d d d d ( 格林公式 )函数在 D 上具有连续一阶偏导数,∫∫∫+=∂∂∂∂LDyxyQ x P y x QP d d d d 或一、格林公式证明:1) 若D 既是 X - 型区域 , 又是 Y - 型区域 , 且⎩⎨⎧≤≤≤≤b x a x y x D )()(:21ϕϕ⎩⎨⎧≤≤≤≤d y c y x y D )()(:21ψψ则y x x Q D d d ∫∫∂∂∫=dcy y y Q d )),((2ψ∫∂∂)()(21d y y xx Q ψψ∫=CBE y y x Q d ),(∫−CAE y y x Q d ),(∫=CBEy y x Q d ),(∫+EACyy x Q d ),(∫−dcyy y Q d )),((1ψ∫=dcy d O d c y xECBA b a D即y x xQD d d ∫∫∂∂∫=L y y x Q d ),(同理可证y x yP D d d ∫∫∂∂−∫=L xy x P d ),(①②①、②两式相加得:()∫∫∫+=∂∂−∂∂LD y Q x P y x y Px Q d d d dL2) 若D 不满足以上条件,则可通过加辅助线将其分割1D nD 2D ()∑∫∫=∂∂−∂∂=n k D y x yPx Q k1d d ()y x yPx Q Dd d ∂∂−∂∂∫∫∑∫=∂+=nk D kyQ x P 1d d ∫+=LyQ x P d d 为有限个上述形式的区域 , 如图)(的正向边界表示k k D D ∂证毕yxO推论: 正向闭曲线 L 所围区域 D 的面积∫−=Lxy y x A d d 21格林公式∫∫∫+=⎟⎠⎞⎜⎝⎛∂∂−∂∂LD y Q x P y x y P x Q d d d d 例如, 椭圆π)20(sin cos :≤≤⎩⎨⎧==θθθb y a x L 所围面积∫−=L xy y x A d d 21∫+=π2022d )sin cos (21θθθab ab ab π=例1. 设 L 是一条分段光滑的闭曲线, 证明d d 22=+∫y x x y x L证: 令,,22x Q y x P ==则yPx Q ∂∂−∂∂利用格林公式 , 得y x x y x Ld d 22∫+022=−=x x ∫∫=Dy x d d 00=例2. 计算,d d e2∫∫−Dyy x 其中D 是以 O (0,0) , A (1,1) ,B (0,1) 为顶点的三角形闭域 . 解: 令, 则2e,0yx Q P −===∂∂−∂∂yP x Q 利用格林公式 , 有∫∫−D yy x d d e2∫∂−=Dyy x d e 2y x OAyd e2∫−=yy yd e102∫−=)e 1(211−−=2e y−xy =yx)1,1(A )1,0(B D O例3. 计算,d d 22∫+−L y x xy y x 其中L 为一无重点且不过原点的分段光滑正向闭曲线.解: 令,022时则当≠+y x 22222)(y x xy x Q +−=∂∂设 L 所围区域为D ,,)0,0(时当D ∉由格林公式知0d d 22=+−∫L y x xy y x ,22yx yP +−=22y x x Q +=y P ∂∂=y xLOθθθd sin cos π2022222∫+=rr r π2=,)0,0(时当D ∈在D 内作圆周,:222r y x l =+取逆时针方向,1D , 对区域1D 应用格∫+−L y x xy y x 22d d ∫+−−l y x x y y x 22d d ∫−+−=l L yx xy y x ∪22d d 0d d 01==∫∫y x D ∫∫+−=+−∴l L y x x y y x y x x y y x 2222d d d d L 1D l记 L 和 l ¯ 所围的区域为林公式 , 得yxO二、平面上曲线积分与路径无关的等价条件定理2. 设D 是单连通域 ,),(),,(y x Q y x P 在D 内具有一阶连续偏导数,(1) 沿D 中任意光滑闭曲线 L , 有.0d d ∫=+L y Q x P (2) 对D 中任一分段光滑曲线 L , 曲线积分(3)y Q x P d d +),(y x u yQ x P y x u d d ),(d +=(4) 在 D 内每一点都有.xQ y P ∂∂=∂∂∫+L y Q x P d d 与路径无关, 只与起止点有关.函数则以下四个条件等价:在 D 内是某一函数的全微分,即(1) 沿D 中任意光滑闭曲线 L ,有.0d d ∫=+L y Q x P (2) 对D 中任一分段光滑曲线L , 曲线积分∫+L y Q x P d d 与路径无关, 只与起止点有关.说明: 积分与路径无关时, 曲线积分可记为设21,L L ∫∫+−+21d d d d L L y Q x P y Q x P ∫+=1d d Ly Q x P ∫−++2d d L yQ x P ∫−+=21d d L L y Q x P ∪0=2L ∫+=2d d L yQ x P ∫+∴1d d L y Q x P 为D 内任意两条由A 到B 的有向分段光滑曲线,则(根据条件(1))∫+=B A y Q x P d d ∫+AB y Q x P d d AB 1L(2) 对D 中任一分段光滑曲线L , 曲线积分(3)y Q x P d d +),(y x u y Q x P y x u d d ),(d +=∫+Ly Q x P d d 与路径无关, 只与起止点有关. 在 D 内是某一函数的全微分,即在D 内取定点),(00y x A 因曲线积分∫+=),(),(00d d ),(y x y x yQ x P y x u ),(),(y x u y x x u u x −∆+=∆则),(y x P =x u x u xx ∆∆=∂∂∴→∆0lim ),(lim 0y x x P x ∆+=→∆θ∫∆++=),(),(d d y x x y x y Q x P ∫∆+=),(),(d y x x y x xP xy x x P ∆∆+=),(θ同理可证y u ∂∂),,(y x Q =因此有y Q x P u d d d +=和任一点B ( x , y ),与路径无关,),(y x x C ∆+),(y x B ),(00y x A 有函数(4) 在 D 内每一点都有.xQ yP ∂∂=∂∂(3)y Q x P d d +),(y x u y Q x P y x u d d ),(d +=在 D 内是某一函数的全微分,即xy uy x u ∂∂∂=∂∂∂22所以设存在函数 u ( x , y ) 使得y Q x P u d d d +=则),(),,(y x Q yu y x P x u =∂∂=∂∂P, Q 在 D 内具有连续的偏导数,从而在D 内每一点都有x Q y P ∂∂=∂∂xy u x Q yx u y P ∂∂∂=∂∂∂∂∂=∂∂∴22,证明 (4) ⇒ (1)设L 为D 中任一分段光滑闭曲线,D D ⊂′(如图) ,上因此在D ′xQ y P ∂∂≡∂∂利用格林公式 , 得y x xQx Q y Q x P L D d d )(d d ∂∂−∂∂=+∫∫∫′D D ′L0=所围区域为证毕(1) 沿D 中任意光滑闭曲线 L , 有.0d d ∫=+L y Q x P (4) 在 D 内每一点都有.x Qy P ∂∂=∂∂说明:根据定理2 , 若在某区域D 内,xQy P ∂∂=∂∂则2) 求曲线积分时, 可利用格林公式简化计算,3) 可用积分法求d u = P d x + Q d y 在域 D 内的原函数:D y x ∈),(00及动点,),(D y x ∈y y x Q x y x P y x u y x y x d ),(d ),(),(),(),(00+=∫∫=xx x y x P 0d ),(0或∫=y y y y x Q y x u 0d ),(),(0则原函数为∫+y y yy x Q 0d ),(∫+x x xy x P 0d ),(若积分路径不是闭曲线, 可添加辅助线;取定点1) 计算曲线积分时, 可选择方便的积分路径;yx 0y 0x O xy4) 若已知 d u = P d x + Q d y ,则对D 内任一分段光滑曲∫+=B Ay y x Q x y x P d ),(d ),(AB u=)()(A u B u −=线 AB ,有yy x Q x y x P ABd ),(d ),(+∫注: 此式称为曲线积分的基本公式(P211定理4). ∫∫=babax F x x f )(d d )(DAB它类似于微积分基本公式:∫=BAu d ())()(x f x F =′其中)()()(a F b F x F ab −==yA xL 例4. 计算,d )(d )3(22y x y x y x L−++∫其中L 为上半24x x y −=从 O (0, 0) 到 A (4, 0).解: 为了使用格林公式, 添加辅助线段,AO D 它与L 所围原式y x y x y x AOL d )(d )3(22−++=∫∪∫∫=Dy x d d 4∫−+++OAyx y x y x d )(d )3(22∫+402d xx 圆周区域为D , 则O例5. 验证y y x x y x d d 22+是某个函数的全微分, 并求出这个函数.证: 设,,22y x Q y x P ==则xQ y x y P ∂∂==∂∂2由定理2 可知, 存在函数 u (x , y ) 使yy x x y x u d d d 22+=∫+=),()0,0(22d d ),(y x yy x x y x y x u )0,(x +=0y y x y d 02∫=yy x yd 02∫2221yx =)0,0(),(y x例6. 验证22d d yx xy y x +−在右半平面 ( x > 0 ) 内存在原函数 , 并求出它.证: 令2222,y x xQ y x y P +=+−=则)0()(22222>∂∂=+−=∂∂x yQ y x x y x P 由定理 2 可知存在原函数∫+−=),()0,1(22d d ),(y x yx xy y x y x u +=0)0(arctan >=x xyx y ∫+y y x y x 022d )0,(x )0,1(),(y x Ox y )0,(x )0,1(),(y x O ∫+−=),()0,1(22d d ),(y x yx xy y x y x u ∫+=y y y 021d yxy y arctan1arctan arctan −+=yx arctan 2π−=∫+−x y x x y 122d 或),1(y )0(arctan>=x xy例7. 设质点在力场作用下沿曲线 L :x y cos 2π=由)2π,0(A 移动到,)0,2π(B 求力场所作的功W解:)d d (2∫−=L y x x y r k 令,,22rx k Q r y k P −==则有)0()(22422≠+−=∂∂y x ry x k y P x Q∂∂=可见, 在不含原点的单连通区域内积分与路径无关..)(22y x r +=其中),(2x y rkF −=s F W Ld ∫⋅=L B Ay x O:AB )d d (2y x x y r kW AB −=∫θθθd )cos (sin 202π2+−=∫k )02π:(sin 2π,cos 2π→==θθθy x k 2π=思考: 积分路径是否可以取?OB AO ∪取圆弧为什么？注意, 本题只在不含原点的单连通区域内积分与路径无关 !LB A y xO 转内容小结判别: P , Q 在某单连通域D 内有连续一阶偏导数,,xQ y P ∂∂=∂∂D y x ∈),(③为全微分方程则求解步骤:方法1 凑微分法;方法2 利用积分与路径无关的条件.1. 求原函数 u (x , y )2. 由 d u = 0 知通解为 u (x , y ) = C .*三、全微分方程使若存在),(y x u y y x Q x y x P y x u d ),(d ),(),(d +=则称0d ),(d ),(=+y y x Q x y x P 为全微分方程.③),(y x yxO 例8. 求解0d )33(d )35(222324=+−+−+y y y x y x x y y x x 解: 因为=∂∂y P 236y y x −,xQ ∂∂=故这是全微分方程. ,0,000==y x 取则有x x y x u xd 5),(04∫=yy y x y x yd )33(0222∫+−+5x =2223y x +3y x −331y+因此方程的通解为Cy y x y x x =+−+332253123)0,(x 法10d )33(d )35(222324=+−+−+y y y x y x x y y x x 求解法2 此全微分方程的通解为 yu ∂∂,)(2y y =′ϕC y x u =),(x u ∂∂, 则有)(d )35(),(324y x y y x x y x u ϕ+−+=∫待定，)()(233225y y y x y x x ϕϕ+−+=两边对 y 求导得④yu ∂∂⑤由④得与⑤比较得331)(yy =ϕ取因此方程的通解为C y y x y x x =+−+33225312332435y y x x −+=22233y y x y x +−=)(3322y y x y x ϕ′+−=例9. 求解0d 1d )(2=−+y x x xy x 解:21x y P =∂∂∵∴ 这是一个全微分方程 .用凑微分法求通解.将方程改写为0d d d 2=−−xx y y x x x 即()(),0d 21d 2=−x y x 故原方程的通解为()021d 2=−xyx 或Cxyx =−221,xQ ∂∂=思考: 如何解方程?0d d )(3=−+y x x y x 这不是一个全微分方程 ,,12x就化成例9 的方程 .,0),(≠=y x µµ使d ),(),(d ),(),(=+y y x Q y x x y x P y x µµ为全微分方程,),(y x µ则称在简单情况下, 可凭观察和经验根据微分倒推式得到为原方程的积分因子.但若在方程两边同乘注:若存在连续可微函数积分因子.内容小结1. 格林公式∫+L y Q x P d d2. 等价条件在 D 内与路径无关.yP x Q ∂∂=∂∂在 D 内有yQ x P u d d d +=yx y P x Q D d d ∫∫⎟⎠⎞⎜⎝⎛∂∂−∂∂=∫+Ly Q x P d d 对 D 内任意闭曲线 L 有0d d =+∫Ly Q x P 在 D 内有设 P , Q 在 D 内具有一阶连续偏导数, 则有为全微分方程0d d =+y Q x P思考与练习1. 设,4:,1:222412=+=+y x l y x L 且都取正向, 问下列计算是否正确 ?∫+−L y x x y y x 22d 4d )1(∫+−=l y x x y y x 22d 4d ∫−=l x y y x d 4d 41∫∫=Dσd 541π5=∫+−L y x x y y x 22d d )2(∫+−=l y x x y y x 22d d ∫−=l x y y x d d 41∫∫=D σd 241π2=提示:时022≠+y x y P x Q ∂∂≠∂∂)1(y P x Q ∂∂=∂∂)2(LO 2y1x2lD2. 设,)56,4(),(42234y y x xy x y x u −+=grad ).,(y x u 求提示:=),(d y x u x xy x d )4(34+y y y x d )56(422−+),(y x u O y x),(y x )0,(x x x x d 04∫=y y y x y d )56(0422∫−+C +551x =322y x +C y +−5x xy x d )4(34+y y y x d )56(422−+∫=),()0,0(y x C+作业P212 2 (1) ; 3 ; 4 (3) ; 5 (1) , (4) ； 6 (2) ,(5) ;*8 (2), (4), (7) ; 9∫∫′′−C C C ∪D O yx a a −C 备用题 1. 设 C 为沿[]y x a x y x a x x a y C d )ln(2d 22222+++++∫222a y x =+从点),0(a 依逆时针),0(a −的半圆, 计算解: 添加辅助线如图 ,利用格林公式 .原式 =3π21a =∫−−a a ya y d )ln 2(∫∫⎢⎣⎡=D 222x a y a ++222x a y +−y x d d ⎥⎦⎤C ′到点D2. 质点M 沿着以AB 为直径的半圆, 从 A (1,2) 运动到+=∫∫D y x d d 2点B (3, 4),到原点的距离,解: 由图知故所求功为AB y x x y d d +−=∫AB (∫=BA ∪AB []x x x d )1(31∫++−2π2−=锐角,其方向垂直于OM , 且与y 轴正向夹角为AB ∫+))d d (y x x y +−)1(21334−+=−−x y AB 的方程F 求变力 F 对质点M 所作的功. ( 1990 考研 ) ,),(x y F −=F 的大小等于点 M 在此过程中受力 F 作用,s F W d ⋅=∫O ),(y x M B A y x,0)1,0(,1=∈F C F 3. 已知曲线积分与路径无关, 其中求由确定的隐函数解:因积分与路径无关 , 故有x F x F x sin cos +−xF x y F y sin sin +=即因此有]d cos d sin [),(y x x x y y x F L −∫0),(=y x F .)(x f y =x y F F y x tan =−x y y tan =′10==x y xy cos 1=x sec =]sin ),([]cos ),([x y y x F yx y x F x ∂∂=−∂∂y ′。

11-3格林公式(ppt文档)

y)dy

D
(
Q x

P y
)dxdy
，
其中 L 取正向．
(11.3.1)
证本定理分三种情形证明．
⑴ 区域 D 既是 x 型区域，也是 y 型区域
由于区域 D 为 x 型区域，则D 可表示为
D {(x, y) | a x b,1(x) y 2(x)}（见图 11-3-1），
例如，区域 D1： x2 y2 1的边界曲线L : x2 y2 1的正向为逆时针方向；
区域 D2 ： x2 y2 1的边界曲线L : x2 y2 1的正向为顺时针方向．
由于区域 D3 ：1 x2 y2 4 边界曲线 L 是由L1 ：x2 y2 1和 L2 ：x2 y2 4
L xdy ydx 2 dxdy ，
2 (x) Pdy
a
1( x) y
b
[P(
a
x,
2
(
x))

P(
x,1
(
x))]dx
，
所以

L
P(
x,
y)dx

D
Pdxdy y
．
又因为区域
D
也是
y
型区域，同理可证

L
Q(
x,
y)dx

D
Qdxdy x
．
15-6
（续证 1）综上，当区域 D 既是 x 型区域，也是 y 型区域时，有

L
P(x,
y)dx

Q(x,
y)dy

D
(
Q x

P y

格林(Green)公式及其应用

格林(green)公式及其应用
• 格林公式简介 • 格林公式的基本性质 • 格林公式的应用 • 格林公式的扩展 • 格林公式的实际例子 • 总结与展望
01
格林公式简介
格林公式的定义
格林公式是一个数学定理，用于描述二维平面上的向量场和路径之间的关系。它指出，在一个封闭的区域内，沿任意路径的积分等于该区域内散度的体积分。
在实变函数中的应用
证明定理
格林公式在证明实变函数中的一些定理中发挥了重要作用，如黎曼定理和克雷洛夫定理等。
求解积分方程
利用格林公式，可以将积分方程转化为边界积分方程，从而简化求解过程。
04
格林公式的扩展
高维格林公式
总结词
高维格林公式是格林公式在高维空间中的推广，它描述了高维空间中向量场和标量场之间的关系。
THANKS
感谢观看
格林公式的变种
总结词
格林公式的变种是原始格林公式的不同形式或应用，它们在特定情况下可能更加方便或有效。
详细描述
随着数学和物理学的发展，人们发现了许多格林公式的变种。这些变种可能在某些特定情况下更加适用，例如在处理非线性问题或复杂边界条件时。了解这些变种有助于我们
更好地理解和应用格林公式。
03
格林公式在数学分析中占有重要的地位，是微积分学中的基本定理之一。它为解决许多复杂的积分问题提供了一种有效的方法，使得许多难以计算的问题变得简单明了。
对未来研究的展望
随着数学和其他学科的发展，格林公式在各个领域的应用越来越广泛。未来，我们可以进一步探索格林公式的各种应用，如数值计算、物理模拟、图像处理等。
解决偏微分方程的实例
总结词
格林公式还可以用于解决偏微分方程的问题，通过将偏微分方程转化为等价的积分方程，可以简化求解过程。

数学分析之格林公式

y
1
A
∂Q ∂ 2 4 = (x + y ) = 2x ∂x ∂x
∂P ∂Q , 即 = ∂y ∂x
1 2 1 4
o
1
x
23 故原式 = ∫0 x dx + ∫0 (1 + y )dy = . 15
区域连通性的分类
为平面区域, 设D为平面区域如果内任一闭曲线所围成为平面区域如果D内任一闭曲线所围成的部分都属于D, 则称D为平面单连通区域为平面单连通区域, 的部分都属于则称为平面单连通区域否则称为复连通区域. 则称为复连通区域
∫ Pdx + Qd y
L
与路径无关, 的起点及终点有关. 与路径无关只与 L 的起点及终点有关 (iii) 是 D 内是某一函数即 d u( x, y) = P dx + Q d y 的全微分, 的全微分,
∂ P ∂Q (iv) 在 D 内处处成立 . = ∂ y ∂x
(ii) 证明 (i) 设 L , L2 为D 内任意两条由到B 的有向分段光滑曲内任意两条由A 1 线, 则
= ∫ F cos α ds − G cos β ds
L
= ∫ F sin(τ , x )ds − G cos(τ , x )ds
L
= ∫ F cos( n, x )ds + G cos( n, y )ds
L
∂Q ∂P ∫∫ ∂x − ∂y dxdy D
=∫ P(x, y)dx +Q(x, y)dy
∫∫ (
D
∂Q ∂ P ) dxd y − ∂x ∂ y
D1
D 1
D2
= ∫∫
+ ∫∫

11.3 格林公式

新课引入
在前面研究过的积分中，重积分和曲线积分都可转化类似地, 为定积分来计算，
曲线积分也可转化为重积分来计算?
本节将要介绍的格林公式给出了平面闭区域 D 上的二重积分与其边界曲线 L 上的曲线积分之间的联系.
另一方面，我们可以利用格林公式得到“平面上积分与路径无关的条件”和“二元函数的全微分求积的充要条件” 。 2019/2/9 1
2019/2/9 4
L1 L1
D
L2
D
L2
L 由 L 与 L 连成 1 2
L 由 L 与 L 组成 1 2
（1）D可以是单连通区域也可以是复连通区域。（2）边界曲线L的正向: 当观察者沿边界行走时, 区域
D总在他的左边.
2019/2/9 5
y
证明:(1)
若区域 D 既是 X 型又是Y 型,即平行于坐标轴的直线和 L至多交于两点.
d x (y ) 1 A
E
y ( x ) 2
D
B
c o a
x (y ) 2 ( x ) Cy 1
D {( x , y ) ( y ) x ( y ), c y d }
D {( x , y ) ( x ) y ( x ), a x b } 1 2
域. D 单连通区域
2019/2/9
D
复连通区域
3
2、格林公式
定理 1 闭区域 D 由分段光滑的曲线 L 围成,函数 P ( x , y )及Q( x , y )在 D 上具有一阶连续偏导数, 则有
Q P ( )dxdy L Pdx Qdy x y D
(1)
其中 L是 D 的取正向的边界曲线。公式(1)叫做格林公式.

11-3格林公式及其应用

复连通区域（有洞）
3
边界曲线L的正向：
L1
D
L2
L1
D
L2
L由L1与L2连成
L由L1与L2组成
边界曲线L的正向：
当观察者沿边界行走时，区域D总在他的左
边的行走方向。
2019年9月7日星期六
4
三、格林公式
定理1 设闭区域D 由分段光滑的曲线L 围
成,函数P( x, y)及Q( x, y)在D 上具有一阶连
第三节格林公式及其应用
(Application of Green formula)
一、问题的提出二、区域连通性的分类三、格林(Green)公式四、格林(Green)公式的简单应用五、曲线积分与路径的无关六、小结
2019年9月7日星期六
1
一、问题的提出
在一元函数的微积分中我们通过NewtonLeibniz公式可以把定积分和原函数在积分区间端点处的值联系起来。
e y2 dxdy ,其中D 是
B 1
D
D
以O(0,0), A(1,1), B(0,1)为顶点
的三角形闭区域.
o
解：令P 0, Q xe y2 ,
则 Q P e y2 , x y
A
x
1
2019年9月7日星期六
9
应用格林公式，有
y
e y2dxdy
xe y2 dy
B
1
D
OA AB BO
D
xe y2dy 1 xex2dx
OA
0
o
1 (1 e1 ). 2
A
x
1
2019年9月7日星期六
10

格林公式的证明

格林公式的证明
格林公式是数学中最基本的定理，它决定了数学中三角函数的性质。

格林公式是由挪威数学家施耐德·格林第一次推导出来的，他在1736年的《集合论的研究》一书中总结出了以下公式：格林公式：
sin(x + y) = sin x cos y + cos x sin y
cos(x + y) = cos x cos y - sin x sin y
下面我们来证明格林公式。

我们从最基本的定义出发，即三角函数的定义：
对于任意的x和y，若把这两个角度组合成一个新的角度z，即z＝x＋y，那么有：
sin z = sina cosb + cosa sinb
cos z = cos a cos b - sina sinb
这就是格林公式了。

下面我们将以上公式加以正式的证明：
我们令两个角α和β的正弦值分别为sinα和sinβ，余弦值分别为cosα和cosβ，令z = α + β，那么：
（1）sinz = sin（α+ β）= 2sina cosβ
（2）cosz = cos（α+ β）= cosα cosβ - sina sinβ
（3）将（1）和（2）代入我们前面的公式，可以得出：
sinz = sina cosβ + cosa sinβ
cosz = cosαcosβ - sina sinβ
即证明格林公式成立！。