形位误差分布规律的相关问题研究
形位误差

形位公差加工后的零件不仅有尺寸误差,构成零件几何特征的点、线、面的实际形状或相互位置与理想几何体规定的形状和相互位置还不可避免地存在差异,这种形状上的差异就是形状误差,而相互位置的差异就是位置误差,统称为形位误差(tolerance of form and position)。
形位公差形位公差术语根据GB/T1182-2008 已改为新术语几何公差包括形状公差和位置公差。
任何零件都是由点、线、面构成的,这些点、线、面称为要素。
机械加工后零件的实际要素相对于理想要素总有误差,包括形状误差和位置误差。
这类误差影响机械产品的功能,设计时应规定相应的公差并按规定的标准符号标注在图样上。
20世纪50年代前后,工业化国家就有形位公差标准。
国际标准化组织(ISO)于1969年公布形位公差标准,1978年推荐了形位公差检测原理和方法。
中国于1980年颁布形状和位置公差标准,其中包括检测规定。
形状公差和位置公差简称为形位公差。
形状公差是指单一实际要素的形状所允许的变动全量。
形状公差用形状公差带表达。
形状公差带包括公差带形状、方向、位置和大小等四要素。
形状公差项目有:直线度、平面度、圆度、圆柱度、线轮廓度、面轮廓度等6项。
通俗点就是,和形状有关的要素。
编辑本段位置公差位置公差是指关联实际要素的位置对基准所允许的变动全量。
定向公差定向公差是指关联实际要素对基准在方向上允许的变动全量。
这类公差包括平行度、垂直度、倾斜度3项。
编辑本段跳动公差跳动公差是以特定的检测方式为依据而给定的公差项目。
跳动公差可分为圆跳动与全跳动。
编辑本段定位公差定位公差是关联实际要素对基准在位置上允许的变动全量。
这类公差包括同轴度、对称度、位置度3项。
编辑本段零件的形位公差图标及其涵义零件的形位公差共14项,其中形状公差6个,位置公差8个,列于下表。
零件的形位公差图标直线度直线度是表示零件上的直线要素实际形状保持理想直线的状况。
也就是通常所说的平直程度。
形位公差标准(GB1184-80)

形位公差标准(GB1184-80)
机械制造中形位误差与圆柱面的尺寸误差一样,是不可避免的。
因此就要考虑,哪些切削表面应加以较严格的控制,并在图样上注出其极限数值。
这是由零件在机器上的位置、功用和装配精度要求来决定的。
零件上圆柱表面的形状误差,在间隙配合中会使间隙分布不均匀,接触不良,从而降低配合精度,加快磨损,减短使用寿命;在过盈配合中,则会使配合各处的过盈量大小不一,影响连接强度。
零件表面的位置误差,除影响配合以外,还影响机器的装配精度及工作时的运动精度。
1、形位公差等级和数值的选用原则
在GB1184-80中,除位置度用计算得出外,对形位公差规定了12个等级,其中,9~12级的数值较大,可以不再图样上一一标注,而对选定的等级在图样中加以说明。
对于需要在图样中加以较严格控制的形位公差值,应根据零件的功能要求,考虑加工的经济性和零件的结构、刚性等因素选定,并需注意下列情况。
1)在同一要素上给出的形状公差值应小于位置公差值。
2)圆柱表面的形状公差值(轴线的直线度除外),一般情况下,应小于其尺寸公差值。
3)平行度公差值应小于其相应的距离公差值。
4)对于下列情况,考虑到加工难易程度和其他参数的影响,在满足零件的功能要求下,适当降低1~1级选用。
A.细长比较大的轴和孔;
B.孔相对于轴;
C.距离较大的轴或孔;
D.宽度较大(一般大于1/2长度)的零件表面;E.线对线和线对面相对于面对面的平行度及垂直度。
2、形状公差标准
直线度、平面度
圆度、圆柱度
3、位置公差标准
平行度、垂直度、倾斜度
同轴度、对称度、圆跳动和全跳动。
形位公差及其误差检测

§3. 1 概述 §3. 2 形状公差 §3. 3 位置公差 §3. 4 公差原则 §3. 5 形位公差的选用 §3.6 形位误差的检测
第三章 形位公差及其误差检测
零件在机械加工过程中由于受到机床夹具、刀具及工艺操作等因
素的影响,将会产生形状误差和位置误差(简称形位误差)。形位
2.按存在状态分类 (1)实际要素。实际要素是指零件上实际存在的要素。在评定 形位误差时,通常用测量得到的要素代替实际要素。 (2)理想要素。理想要素是指具有几何意义的要素,它们不存 在任何误差。机械零件图上表示的要素均为理想要素。
上一页 下一页
§ 3.1 概述
3.按所处地位分类 (1)被测要素。被测要素是指图样上给出形状或(和)位置公差
为了研究形位公差和形位误差,可从不同的角度对几何要素 进行分类。
1.按结构特征分类
下一页
§ 3.1 概述
(1)轮廓要素。轮廓要素是指构成零件外形的点、线、面各要 素,如图3-1中的球面、圆锥面、圆柱面、平面和圆锥面、圆柱 面的素线以及圆锥顶点。 (2)中心要素。中心要素是指轮廓要素对称中心所表示的点、线、 面各要素,如图3-1中的圆柱面的轴线、球面的球心。
误差会影响机械零件的工作精度、连接强度、运动平稳性、密封
性、耐磨性、噪声和使用寿命等,因而影响着该零件的质量和互
换性。例如,光滑圆柱形零件的形状误差会使其配合间隙不均匀,
局部磨损加快,降低工作寿命和运动精度等;机床工作表面的直
线度、平面度不好,将影响机床刀架的运动精度,进而影响产品
的加工质量。为了保证机械产品的质量和零件的互换性,在设计
四、形位公差带
形位公差带是用来限制被测实际要素变动的区域。这个区域可以是平
形位误差和要素的定义

测量误差越小,提取实际要素越接近实际(组成)要素。 拟合组成(轮廓)要素 associated integral feature — 按规定的方 法由提取组成要素形成的并具有理想形状的组成(轮廓)要素。
老标准未出现该要素,因它主要用于测量。现为统一测量方 法,提出此概念。它的实质是找出提取(测得)实际要素之其相 应的理想轮廓要素。
形位误差和要素
一 、形位误差产生的因素 由于加工过程中工件在机床上的定位误差、刀具与工件的相
对运动不正确、夹紧力和切削力引起的零件变形、工件的内应力 的释放等原因,完工零件会产生各种形状和位置误差。
形状误差 例如:在车削圆柱表面时,刀具运动方向与零件旋转轴线不
平行,会使完工零件表面呈圆锥形。
又如:在车削以顶针支承的细长轴时,切削力过大使完工零 件表面呈 鼓形。
圆锥面
圆柱面
圆台面
球面
轴线
素线
球心
几何(形位)公差研究对象就是几何要素 - 点、线、面。
《GB 1183-80 术语和定义》标准,96取消,02另新订。
B ) 尺寸要素 feature of size — 由一定大小的线性尺寸或角度尺寸 确定的几何形状。
注:尺寸要素可以是圆柱形、球形、两平行对应面、圆锥形等。
又如:钻床的主轴与工作台之 间若不垂直,则加工的孔与端面亦 有 垂直度误差。
又如:多孔钻模因钻套孔心距的误差,使零件上加工出的成 组孔产生位置度误差。同样,多孔的冲模也会由于模具的误差使 零件的成组孔产生位置度误差。
上述例子举了影响形位精度的各主要原因,我们必须根据 具体加工条件,对影响因素进行分析,采取有效措施,以消除 或减少这些因素的影响,来满足图样上给定的形位公差要求。
形位误差和形位公差
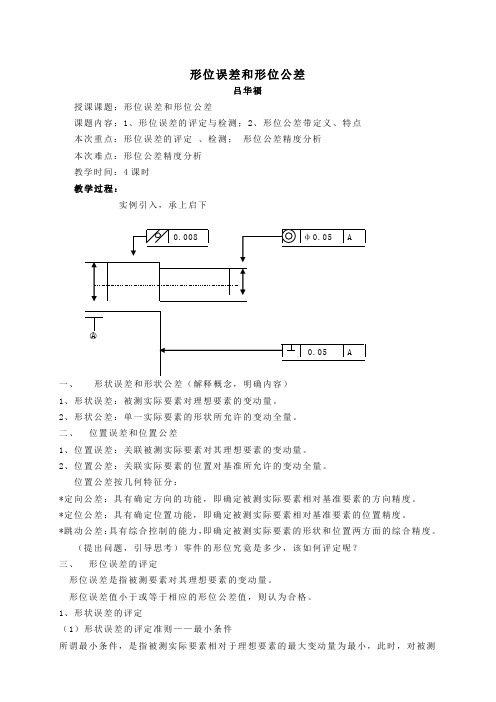
形位误差和形位公差吕华福授课课题:形位误差和形位公差课题内容:1、形位误差的评定与检测;2、形位公差带定义、特点本次重点:形位误差的评定、检测;形位公差精度分析本次难点:形位公差精度分析教学时间:4课时教学过程:实例引入,承上启下一、形状误差和形状公差(解释概念,明确内容)1、形状误差:被测实际要素对理想要素的变动量。
2、形状公差:单一实际要素的形状所允许的变动全量。
二、位置误差和位置公差1、位置误差:关联被测实际要素对其理想要素的变动量。
2、位置公差:关联实际要素的位置对基准所允许的变动全量。
位置公差按几何特征分:*定向公差:具有确定方向的功能,即确定被测实际要素相对基准要素的方向精度。
*定位公差:具有确定位置功能,即确定被测实际要素相对基准要素的位置精度。
*跳动公差:具有综合控制的能力,即确定被测实际要素的形状和位置两方面的综合精度。
(提出问题,引导思考)零件的形位究竟是多少,该如何评定呢?三、形位误差的评定形位误差是指被测要素对其理想要素的变动量。
形位误差值小于或等于相应的形位公差值,则认为合格。
1、形状误差的评定(1)形状误差的评定准则——最小条件所谓最小条件,是指被测实际要素相对于理想要素的最大变动量为最小,此时,对被测实际要素评定的误差值为最小。
(2)形状误差值的评定评定形状误差时,形状误差数值的大小可用最小包容区域(简称最小包容区域)的宽度或直径表示。
3个区域比较,引出最小条件、最小区域的概念,用以评定形状误差。
2、位置误差的评定*定向误差是被测实际要素对一具有确定方向的理想要素的变动量,该理想要素的方向由基准确定。
定向误差值用定向最小包容区域(简称定向最小区域)的宽度或直径表示。
定向最小区域是指按理想要素的方向包容被测实际要素时,具有最小宽度或直径的包容区域。
(通过定向误差的评定分析,比较定向最小区域与最小区域的差别。
)*定位误差是被测实际要素对一具有确定位置的理想要素的变动量。
轴类零件形位误差在机床上的测量技术研究
而保 证 轴 类 零件 形 位 误 差 在 机 床 上 的 测 量 准 确 度 。
把 上 述 两 种 分 离 方 法 编 制 为计 算 机 测 量 控 制软 件 加
上 适 当 的 测 量 装 置 , 而 可 以 在 机 床 上 测 量 轴 类 零 从 件 的形 位 误 差 。
维普资讯
轴 类 零 件 形 位 误 差 在 机 床 上 的 测 量 技 术 研 究
黄 风 山 方 忆 湘
( 河北 科 技 大 学 , 家庄 石 005 ) 5 0 4
摘
要
本文论 述 了采 用误 差分 离技 术在 机 床上测 量 轴 类 零 件形 位 误 差 的 原 理 、 法 , 出 了该 方法 的数 据 方 给 误 差分离 机床 轴类 零件 形 位 误差 ’
图 1
*
河 北省教 育厅 科研计 划项 目
计 量 技 术 2 0 o8 0 2 N
维普资讯
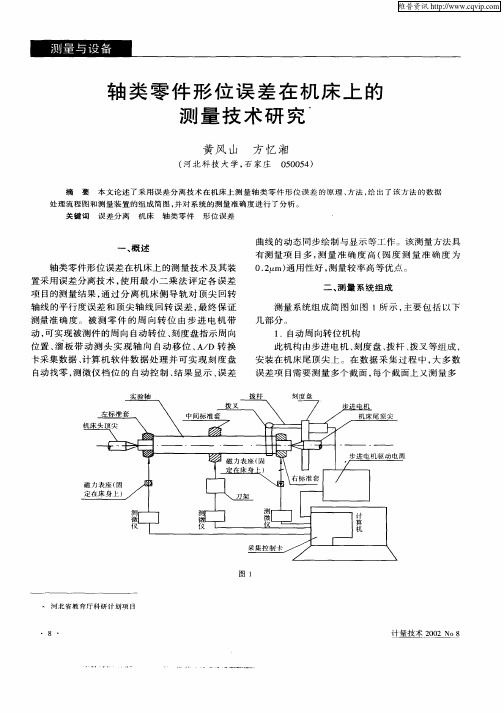
个 点 , 机 构 可 以 实 现 被 测 件 的周 向 自动 转 位 。步 此
进 电机 型 号 为 5 B 0 3 工 作 在 3相 6拍 方 式 , 距 5F0 , 步 为 1 5度 , 进 电机 输 出 轴 与 刻 度 盘 之 间 的 传 动 比 . 步 为 6 1 所 以步 进 电 机 转 一 拍 , 度 盘 转 动 1 5 6= :, 刻 ./
处理流 程 图和 测量装 置 的组 成简 图 , 并对 系统 的测 量 准确 度进 行 了分析 。 关键 词
一
、
概 述
曲线 的 动 态 同步 绘 制 与 显 示 等工 作 。该 测 量方 法 具
有测 量 项 目多 , 量 准 确 度 高 ( 度 测 量 准 确 度 为 测 圆
机械零件形位精度设计的研究

机械零件形位精度设计的研究【摘要】正确合理地进行形位精度设计,对保证机器的功能要求、提高经济效益十分重要。
本文文详细阐述了形位精度设计即形位公差项目,形位公差值,基准要素的选用考虑的因素与方法。
【关键词】形位公差项目;形位公差值;基准要素零件的形位误差对机器、仪器的正常使用有很大的影响,同时也会直接影响到产品质量、生产效率与制造成本。
因此正确合理地形位精度设计,对保证机器的功能要求、提高经济效益十分重要。
形位精度设计的主要内容包括:选择形位公差项目,确定形位公差值,基准要素的选用,按标准规定进行图样标注。
1 形位公差项目的选用选择形位公差项目可根据以下几个方面:1.1 零件的几何特征零件加工误差出现的形式与零件的几何特征有密切联系。
如圆柱形零件会出现圆柱度误差,平面零件会出现平面度误差,凸轮类零件会出现轮廓度误差,阶梯轴、孔会出现同轴度误差,键槽会出现对称度误差等。
1.2 零件的功能要求形位误差对零件的功能有不同的影响,一般只对零件功能有显著影响才规定合理的形位公差。
1.2.1 保证零件的工作精度例如,机床导轨的直线度误差会影响导轨的导向精度,使刀架在滑板的带动下作不规则的直线运动,应该对机床导轨规定直线度公差;滚动轴承内、外圈及滚动体的形状误差,会影响轴承的回转精度,应对其给出圆度或圆柱度公差;在齿轮箱体中,安装齿轮副的两孔轴线如果不平行,会影响齿轮副的接触精度和齿侧间隙的均匀性,降低承载能力,应对其规定轴线的平行度公差;机床工作台面和夹具定位面都是定位基准面,应规定平面度公差等。
1.2.2 保证联结强度和密封性例如,气缸盖与缸体之间要求有较好的联结强度和很好的密封性,应对这两个相互贴合的平面给出平面度公差;在孔、轴过盈配合中,圆柱面的形状误差会影响整个结合面上的过盈量,降低联结强度,应规定圆度或圆柱度公差等。
1.2.3 减少磨损,延长零件的使用寿命例如,在有相对运动的孔、轴间隙配合中,内、外圆柱面的形状误差会影响两者的接触面积,造成零件早期磨损失效,降低零件使用寿命,应对圆柱面规定圆度、圆柱度公差;对滑块等作相对运动的平面,则应给出平面度公差要求等。
基于CMM(三坐标测量机)的形状误差测量及MATLAB实现

基于CMM(三坐标测量机)的形状误差测量及MATLAB实现雷萍(陕理工机械工程学院测控技术与仪器07级1班,陕西汉中 723003)指导教师:张士勇[摘要]形位误差的测量在几何量精密测量中占有十分重要的地位。
基于CMM的形状误差测量在工程应用中有着重要的价值。
本次设计在利用CMM获取测量数据的基础上,根据国家标准中形状误差的定义和评定标准,建立了形状误差评定的求解数学模型,然后利用MATLAB软件进行误差分析处理。
在一定的基础上解决了对形状误差的评定,利用MATLAB软件编程实现了形状误差的评定,并对测量仪器引起的误差做了一定的分析。
[关键字]形状误差,CMM,误差处理,MATLAB,数学模型Based on CMM (the three coordinate measuring machine ) shape error measuring and MATLABAuthor: Lei Ping(Grade06,Class1,Major Measuring & Control Technology and Instrumentation,Mechanical Engineering Dept.,Shaanxi University of Technology,Hanzhong723003,Shaanxi)Tutor: Zhang ShiyongAbstract:Measurement of form and position errors in the geometrical precision measurement plays a very important position. The CMM measurement error based on the shape has important applications in engineering value. The design according to the national standard definitions and evaluation criteria constructs a solving shape model of error evaluation and error analysis based on CMM measurement data,and uses MA TLAB software processing.In a certain sense, this design solves the assessment of a certain shape error,and uses MA TLAB software in the assessment of shape error .it also analyzes the error of measuring instruments .Keywords:shape error, CMM(coordinate measuring machine) ,error handling, MA TLAB solving shape.目录引言 (1)1 绪论 (2)1.1形状误差评定的研究意义 (2)1.2形状误差研究现状 (2)1.3三坐标机测量方法及其运用 (3)1.3.1 三坐标机测量方法与常规方法的差别 (3)1.3.2 三坐标测量机的运用 (3)1.4本次毕业设计的内容 (5)1.4.1 课题意义 (5)1.4.2. 课题背景 (5)2 形状误差测量及数学建模 (6)2.1.优化算法概念 (6)2.2 插值 (6)2.3 直线度的数学建模 (7)2.4 平面度的数学建模 (8)2.4.1 平面度误差定义 (8)2.4.2 平面度误差的测量及最小二乘法建模 (8)2.5 圆度的数学建模 (8)2.5.1 圆度误差的定义和评定方法 (8)2.5.2 最小二乘圆法建模 (9)2.5.3 最小外接圆法建模 (11)2.5.3 最小外接圆法建模 (11)2.5.4 最大内接圆法建模 (11)2.6 圆柱度建模 (12)2.6.1 圆柱度定义和评定方法 (12)2.6.2 最小区域圆柱法 (12)2.6.3 最大内接圆柱法 (12)2.6.4 最小二乘圆柱法 (12)3 测量数据的采集 (14)3.1 直线度误差的定义及检测方法的分类 (14)3.2 平面度误差的定义及检测方法的分类 (15)3.3 圆度误差的定义及检测方法 (17)3.4 圆柱度误差的定义及检测方法 (17)4 MATLAB的学习 (19)4.1 MATLAB的概述 (19)4.2 MATLAB的特点及优点 (19)4.3 MATLAB软件数值计算 (21)4.4 MATLAB的运行环境与安装 (21)4.5 变量和数据操作 (22)4.5.1 预定义变量 (22)4.5.2 MATLAB常用数学函数 (22)4.5.3 MATLAB运算 (22)4.6 MATLAB程序设计 (23)4.6.1 M文件概述 (23)4.6.2 程序控制结构 (23)4.6.3 函数文件的基本结构 (23)4.7 MATLAB绘图 (24)4.7.1 二维曲线的绘制 (24)4.7.2 三维图形 (24)4.7.3 设置曲线样式图形标注与坐标控制 (25)5 程序流程图及数据处理 (26)5.1 直线度 (26)5.2 平面度 (27)5.3 圆度 (30)5.4 圆柱度 (31)6 测量误差分析 (34)6.1测量误差概述 (34)6.2误差分析 (35)结束语 (36)致谢 (37)参考文献 (38)附录 A 外文翻译引言在科学技术快速发展的推动下,人们对产品的功能要求越来越高,对零件各项精度的要求也在提高,而且随着生产的快速发展和产品批量增加,单一的尺寸公差早已满足不了产品装备的互换性要求,必须把形状和位置公差结合起来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
形位误差分布规律的相关问题研究
【摘要】形位误差分布规律对机械加工有很重要的影响,因此,本文以其中的位置度误差分布规律、行为测量误差以及形位误差分布规律和检测方案之间的关系为研究对象,希望有助于深化对形位误差分布规律的认识。
【关键词】形位误差分布规律;位置度误差;行为测量误差
形位误差是机械加工等领域经常会涉及到的一个名词,通俗地讲,形位误差就是形状与位置的误差。
形状误差通常被认为指的是被测要素对其理想要素的变动量。
而位置误差通常指的是被测实际要素对某一具有确定方向的理想要素的变动量。
形位误差尤其自身的分布规律,它对相关机械生产和加工的精密度和质量有着直接的影响,应用价值非常大[1]。
为了对形位误差分布规律有更深入的了解,本文以形位误差分布规律中的相关问题为研究对象,希望对促进机械加工的发展有一定的启示。
本文的研究对象是以典型工序加工的典型孔组,其中典型工序具体指的是通用或专用钻床和与之相配套的钻模板,而典型孔组指的是矩形或圆周分布的孔组。
1.位置度误差分布规律的研究
位置度误差是形位误差的一个重要组成部分,其误差控制也是形位误差控制的关键之一,因此,对其分布规律的研究有重大的价值和意义。
1.1 位置度坐标误差的分布规律
从当前采用的位置度误差定义和它的评定原则来看,位置度坐标误差是被测要素位置度误差的两个分量:
△x=△xi,△y=△yi
同时它还满足:
f=2·=2max{}
f指的是位置度误差,1=1,2,3,…n指的是被测孔组的孔数。
在研究位置度误差的分布规律时,要特别注意,对△x和△y,这两个位置度坐标误差都要有明确的了解,这样可以有效确保研究足够充分和深入。
而经过研究后发现,△x和△y都服从正态分布,且它们的方差并不一定是相等的。
1.2 位置度误差的分布规律
理论分析:
在被测要素完工后,由于会受到多种外界因素的干扰,不可避免地会出现位置度坐标误差。
根据当前采用的位置度误差定义和它的评定原则,位置度误差为:
f=2·
其中的△x和△y在加工出来的同一批零件中都是相互独立的随机变量,而且它们都呈正态分布。
实际上,求位置度误差分布规律就是在求随机变量R=。
通过利用△x和△y的联合分布密度,再结合分布函数理论,就可以从中推导出R=的分布函数F(F0时,从分布函数定义得出
F(F<r)=(x,y)dxdy=(x)·(y)dady
这就从理论上证明了当△x和△y,这两个位置度坐标误差相互独立并服从正态分布时,任意方向的位置度误差会服从瑞利分布。
不过,这只是理论计算的结果,至于是否与实际负荷,还需要通过抽样统计才能确定。
2.行位测量误差分析
对当前所有有关检测的研究分析工作而言,对测量精度的分析直接影响着测量结果的可靠性,行位测量误差的分析工作同样如此。
2.1 行位测量精度相关概念的介绍
当前与行位测量精度密切相关的概念主要有以下四个:
形位测量总误差。
它指的是形位误差所测得的数值与其真值的差,它是形位要素误差、测量误差和方法误差这三种的一个综合反映。
行为要素误差。
指的是用测得要素取代实际要素而引起的误差。
因为测点数是有限的,所以在进行形位误差测量时不得不以测得要素来代表实际要素,这样就必然导致形位要素误差存在于所有的形位误差测量里。
形位测量误差:它指的是因尺寸测量误差而导致的误差。
形位误差测量通常来说都是间接测量,这样就不可避免地使得尺寸测量误差会或多或少地影响形位测量总误差。
形位方法误差。
指的是因采用近似方法来检测和评定形位误差而导致的误差。
2.2 形位测量误差的研究
2.2.1 形位测量误差的近似表达
当前的绝大多数形位误差项目可以表达为以下两种方式:
f1=k (1)
或者是f2=K (2)
因为通过测量尺寸可以有效修正它的已定系统误差,因此,这时候形位误差是随机误差。
2.2.2 误差限的确定
如果已知形位测量误差的分布规律,那么接着就可以求出其误差限了。
假设X1、X2各自的测量极限误差为△1lim和△2lim,那么:
△1lim=±kσ1,△2lim=±kσ2
当它们在同一个置信概率(置信概率设为P)下,其形位测量极限误差为:
△lim=±kσ
=±k
=±
3.形位误差分布规律和检测方案之间的关系
这里指的是,同一批已完工零件里的其中一项形位误差的分布规律会不会随着检测方案的变动而相应的发生变动。
当前,业界普遍认为当采用不同的检测方案时,该项形位误差的分布规律极可能出现变动,不过也同时出现了一些不同的声音,为了深入揭示这一关系,笔者在此对分布规律与检测方案的关系进行一番分析。
根据形位误差的相关定义与评定原则,结合相应的检测规定就能够得出前面的式(1)和式(2)的函数式,式子中的X1、X2指代的是随机变量,当这两个机械加工中生产的误差分量相互独立并服从正态分布的话,那么它们的分布密度函数则为:
f()=
式子中的=r/,0=X0/
X0、指代的是差值,而r=(X1-X2)的算术平均值和标准差也可以证明式(2)中表示的形位误差服从了瑞利分布,它的分布密度函数是:
f(r)=
式子中的就是式(2)里误差分量的标准差了。
通过上面的研究,可以看出任意方向上的各种误差(直线度、平行度=垂直度等),都要服从瑞利分布,而不是绝对正态分布。
这样就很清楚地看到,形位误差的分布规律与检测方案并无关系,它是由工艺条件决定的[2]。
总而言之,通过上面的所有论述可以得出下面几个结论:
任意方向上的位置度误差要服从于瑞利分布;
形位测量误差服从正态分布;
形位误差分布规律是由工艺条件决定的,和检测方案不存在任何关联性。
参考文献
[1]机械工业部标准化研究所.形状和位置公差原理及应用[M].北京:机城工业出版社,1983:55-58.
[2]复旦大学.概率论[M].北京:高等教育出版社,1979:32-27.。
