资本资产定价模型(CAPM(PPT44页)
合集下载
资本资产定价模型PPT课件

资产定价的随机过程
随机过程的基本概念
随机过程是描述一系列随机事件的数学模型,其中每个事件的发生都具有不确定性。在资产定价的上下文中,随 机过程通常用于描述资产价格的变动。
资本资产定价模型的随机过程
资本资产定价模型假设资产价格的变动遵循随机过程,并且这种变动与资产的预期回报和风险有关。通过建立适 当的随机过程模型,可以进一步研究资产价格的动态行为和风险特征。
发展历程
起源
资本资产定价模型起源于20世纪60年代,由经济学家威廉·夏普、 约翰·林特纳和简·莫辛共同发展。
发展
在随后的几十年中,CAPM经历了多次修订和完善,以适应金融市 场的变化。
应用
资本资产定价模型被广泛应用于投资组合管理、风险评估和资本预算 等领域。
发展历程
起源
资本资产定价模型起源于20世纪60年代,由经济学家威廉·夏普、 约翰·林特纳和简·莫辛共同发展。
发展
在随后的几十年中,CAPM经历了多次修订和完善,以适应金融市 场的变化。
应用
资本资产定价模型被广泛应用于投资组合管本资产定价模型用于确定投资 组合的风险和预期回报,帮助投 资者在风险和回报之间做出权衡。
风险评估
通过CAPM,投资者可以评估特 定资产或投资组合的风险,并与 其他资产或基准进行比较。
主要发现
是一种用于评估风险和预期回报之间关系的金融模型,主要用于投资组合管理 和风险评估。
CAPM的核心思想
资本的预期收益率由两部分组成,一部分是无风险利率,另一部分是风险溢价, 即风险超过无风险资产的部分。
目的和目标
目的
通过理解CAPM,投资者可以更准确 地评估投资的风险和预期回报,从而 做出更明智的投资决策。
资本资产定价模型概述(ppt42张)

6、可以在无风险折现率R的水平下无限制地借 入或贷出资金; 7、所有投资者对证券收益率概率分布的看法一 致,因此市场上的效率边界只有一条; 8、所有投资者具有相同的投资期限,而且只有 一期; 9、所有的证券投资可以无限制的细分,在任何 一个投资组合里可以含有非整数股份;
10、税收和交易费用可以忽略不计; 11、市场信息通畅且无成本; 12、不考虑通货膨胀,且折现率不变; 13、投资者具有相同预期,即他们对预期收益率、 标准差和证券之间的协方差具有相同的预期值。 上述假设表明:第一,投资者是理性的,而且严格 按照马科威茨模型的规则进行多样化的投资,并将 从有效边界的某处选择投资组合;第二,资本市场 是完全有效的市场,没有任何磨擦阻碍投资。
又由(7.3)
dv 1 dE ( r E ( r )E ( r c) M j)
于是
d d d v c c d Er ( c) d vd Er ( c)
2 2 [ ( 1 v ) ( 1 2)c v o v ( r , r ) v ]/ j j m M c Er ( M) Er ( j)
假定2:针对一个时期,所有投资者的预期 都是一致的。
这个假设是说,所有投资者在一个共同的时期内 计划他们的投资,他们对证券收益率的概率分布 的考虑是一致的,这样,他们将有着一致的证券预 期收益率﹑证券预期收益率方差和证券间的协方 差。同时,在证券组合中,选择了同样的证券和同 样的证券数目。 这个假设与下面的关于信息在整个资本市场中畅 行无阻的假设是一致的。
故
2 c o v ( r , r ) d j M M c d Er ( c)v Er ( M) Er ( j) ) c( 1
管理学投资学PPT第章资本资产定价模型

问题:
❖若某一个股票未包含在最优资产组合中,
会怎样?
2024/6/29
21
图 9.1 The Efficient Frontier and the
Capital Market Line
2024/6/29
22
9.1.2 消极策略的有效性
理由:
❖市场的有效性
❖投资于市场投资组合指数这样一个消极策略是有
26
▪ β系数。美国经济学家威廉·夏普提出的风险衡量
指标。
▪
用它反映资产组合波动性与市场波动性关系(
在一般情况下,将某个具有一定权威性的股指(
市场组合)作为测量股票β值的基准)。
▪ 如果β值为1.1,表明该股票波动性要比市场大盘
高10 %,说明该股票的风险大于整个市场的风险
,当然它的收益也应该大于市场收益,因此是进
则其收益 - 风险比率为:
wGE [ E (rGE ) rf ] E (rGE ) r f
wGE Cov(rGE , rM ) Cov(rGE , rM )
2024/6/29
25
9.1.4 单个证券的期望收益
市场组合M与CML相切,其收益风险比率为:
E (rM ) rf
2
M
(风险的市场价格)
率应该增加的数量。
▪ 在金融世界里,任何资产组合都不可能超越CML
。由于单个资产一般来说,并不是最优的资产组
合,因此,单个资产也位于该直线的下方。
2024/6/29
14
证券市场线
▪ 资本市场线描述了有效组合的预期收益率和标准
差之间的均衡关系―有效资产组合定价模型。
▪ 问题:
▪ (1) 单个风险资产的预期收益率和标准差之间
❖若某一个股票未包含在最优资产组合中,
会怎样?
2024/6/29
21
图 9.1 The Efficient Frontier and the
Capital Market Line
2024/6/29
22
9.1.2 消极策略的有效性
理由:
❖市场的有效性
❖投资于市场投资组合指数这样一个消极策略是有
26
▪ β系数。美国经济学家威廉·夏普提出的风险衡量
指标。
▪
用它反映资产组合波动性与市场波动性关系(
在一般情况下,将某个具有一定权威性的股指(
市场组合)作为测量股票β值的基准)。
▪ 如果β值为1.1,表明该股票波动性要比市场大盘
高10 %,说明该股票的风险大于整个市场的风险
,当然它的收益也应该大于市场收益,因此是进
则其收益 - 风险比率为:
wGE [ E (rGE ) rf ] E (rGE ) r f
wGE Cov(rGE , rM ) Cov(rGE , rM )
2024/6/29
25
9.1.4 单个证券的期望收益
市场组合M与CML相切,其收益风险比率为:
E (rM ) rf
2
M
(风险的市场价格)
率应该增加的数量。
▪ 在金融世界里,任何资产组合都不可能超越CML
。由于单个资产一般来说,并不是最优的资产组
合,因此,单个资产也位于该直线的下方。
2024/6/29
14
证券市场线
▪ 资本市场线描述了有效组合的预期收益率和标准
差之间的均衡关系―有效资产组合定价模型。
▪ 问题:
▪ (1) 单个风险资产的预期收益率和标准差之间
第五章-资本资产定价模型PPT课件

第五章 资本资产定价模型
2021/3/12
1
第五章 资本资产定价模型
资本资产定价模型(CAPM)是现代金融学的奠基石。 CAPM由威廉·夏普、约翰·林特、简·莫辛分别于 1964、1965、1966年独立提出。 研究当投资者按照Markowitz建议的方式行动时,市场达 到均衡时资产的预期收益率与风险之间的关系。
2021/3/12
9
二、相关的推导
(二)所有投资者都选择市场资产组合作为他们的最优 风险资产组合。
由于投资者按照马可维茨的方法进行投资选择,其持有 的组合是最优风险资产组合,因此它一定在有效边界上, 而且与最优资本配置线相切。
市场组合与无风险资产构成的资本配置线被称为资本 市场线。(CML,Capital Market Line)
•资本资产定价模型的基本形式:
并定义系数:
任意风险资产的风险溢价与市场组合的风险溢价成正比,
该比例系数称为 ᵝ系数,衡量的是单位资产对市场组合
风险的202贡1/3/献12 率。
16
实际上,我们可以从ᵝ取值的大小来区分 股票类型:
ᵝ>1的股票被称为“攻击性股票”,市场上升时其
升幅较大;
ᵝ<1的股票被称为“防御性股票”,市场上升时其升
2021/3/12
10
E(r)
rf •
0
2021/3/12
M
•
•B
•A
11
哪一条资本市场线是最优的呢?
2021/3/12
12
为什么所有的投资者都持有市场资产组合
• 投资者在一个什么样的价位上才愿意将该只股票纳 入其最优风险资产组合。 当某只股票需求为零时,股价会下跌,直至它对于 投资者的吸引力超过任意其它一只股票的吸引力,并进 入到投资者的最优资产组合的构成之中,从而使该股票 价格回升到某一均衡水平
2021/3/12
1
第五章 资本资产定价模型
资本资产定价模型(CAPM)是现代金融学的奠基石。 CAPM由威廉·夏普、约翰·林特、简·莫辛分别于 1964、1965、1966年独立提出。 研究当投资者按照Markowitz建议的方式行动时,市场达 到均衡时资产的预期收益率与风险之间的关系。
2021/3/12
9
二、相关的推导
(二)所有投资者都选择市场资产组合作为他们的最优 风险资产组合。
由于投资者按照马可维茨的方法进行投资选择,其持有 的组合是最优风险资产组合,因此它一定在有效边界上, 而且与最优资本配置线相切。
市场组合与无风险资产构成的资本配置线被称为资本 市场线。(CML,Capital Market Line)
•资本资产定价模型的基本形式:
并定义系数:
任意风险资产的风险溢价与市场组合的风险溢价成正比,
该比例系数称为 ᵝ系数,衡量的是单位资产对市场组合
风险的202贡1/3/献12 率。
16
实际上,我们可以从ᵝ取值的大小来区分 股票类型:
ᵝ>1的股票被称为“攻击性股票”,市场上升时其
升幅较大;
ᵝ<1的股票被称为“防御性股票”,市场上升时其升
2021/3/12
10
E(r)
rf •
0
2021/3/12
M
•
•B
•A
11
哪一条资本市场线是最优的呢?
2021/3/12
12
为什么所有的投资者都持有市场资产组合
• 投资者在一个什么样的价位上才愿意将该只股票纳 入其最优风险资产组合。 当某只股票需求为零时,股价会下跌,直至它对于 投资者的吸引力超过任意其它一只股票的吸引力,并进 入到投资者的最优资产组合的构成之中,从而使该股票 价格回升到某一均衡水平
第6讲 资本资产定价模型(CAPM) (《金融经济学》PPT课件)

第6讲 资本资产定价模型(CAPM)
6.1 从组合选择到市场均衡
《
金
融 经
市场组合M是什么样的?
济 学
市场组合就是包含了所有风险资产的整个市场
二
五 讲
这么个依赖于大量前提条件(各类资产的收益波动状况)的复杂均值方差优化
》 配
问题的结果M,怎么会这么巧就和现实中的整个市场一模一样?
套 课
但结果就是这么巧,也必须这么巧
对市场所做的简化假设
五 讲
没有交易成本(佣金、买卖价差等)
》
配 套
没有税收
课 件
所有资产都可以任意交易,并且无限可分
完全竞争:所有人都是价格的接受者,没有影响价格的能力
对投资者的假设(所有人都求解均值-方差问题)
所有人都以均值方差的方式选择投资组合:偏好更高的期望回报率,以及更低 的回报率波动率
i
市场组合M处,否则与CML
市场组合
定义矛盾
σ
0
7
6.4 CAPM的第二种论证
基于组合构建的CAPM论证(续)
《
金
融 经
济
学
由曲线与CML在M处相切得dE到(rw)
E(rM ) rf
二 五
d (rw ) w0
M
由求导法则及E(r )的表达式可知 讲
》
配
套
课
件
wdE(rw ) dE(rw ) d (rw ) dw
所有资产(包括无风险资产)都可以任意买空卖空
一致预期:所有人针对相同的时间区间(1期)考虑投资问题,并对资产的预期 回报率和预期波动率状况{E(r1̃ ), E(r2̃ ), ..., E(rñ ), σ(r1̃ ), σ(r2̃ ), ..., σ(rñ )}有相同预期
6.1 从组合选择到市场均衡
《
金
融 经
市场组合M是什么样的?
济 学
市场组合就是包含了所有风险资产的整个市场
二
五 讲
这么个依赖于大量前提条件(各类资产的收益波动状况)的复杂均值方差优化
》 配
问题的结果M,怎么会这么巧就和现实中的整个市场一模一样?
套 课
但结果就是这么巧,也必须这么巧
对市场所做的简化假设
五 讲
没有交易成本(佣金、买卖价差等)
》
配 套
没有税收
课 件
所有资产都可以任意交易,并且无限可分
完全竞争:所有人都是价格的接受者,没有影响价格的能力
对投资者的假设(所有人都求解均值-方差问题)
所有人都以均值方差的方式选择投资组合:偏好更高的期望回报率,以及更低 的回报率波动率
i
市场组合M处,否则与CML
市场组合
定义矛盾
σ
0
7
6.4 CAPM的第二种论证
基于组合构建的CAPM论证(续)
《
金
融 经
济
学
由曲线与CML在M处相切得dE到(rw)
E(rM ) rf
二 五
d (rw ) w0
M
由求导法则及E(r )的表达式可知 讲
》
配
套
课
件
wdE(rw ) dE(rw ) d (rw ) dw
所有资产(包括无风险资产)都可以任意买空卖空
一致预期:所有人针对相同的时间区间(1期)考虑投资问题,并对资产的预期 回报率和预期波动率状况{E(r1̃ ), E(r2̃ ), ..., E(rñ ), σ(r1̃ ), σ(r2̃ ), ..., σ(rñ )}有相同预期
资本资产定价模型 (PPT 55张)

i
上式结论也适用于由无风险资产和风险资产组合构 成的投资组合的情形。在图(7-9)中,这种投资组 合的预期收益率和标准差一定落在AB线段上。
11
投资于无风险资产A和风险资产组合B的可行集 ——许多线段AB构成的区域
R
p
﹡D
R r i f R r p f P
Ri
B
★
i
A(rf ) ★
5
二、资本市场线 CML
(一)允许无风险贷出下的可行集与有效集 1.无风险贷款或无风险资产的定义 无风险贷款相当于投资于无风险资产,其收益是确定的, 其风险(标准差)应为零。 无风险资产收益率与风险资产收益率之间的协方差也等于 零。 现实生活中,到期日和投资期相等的国债是无风险资产。
为方便起见,常将1年期的国库券或货币市 场基金当作无风险资产。
17
(二)无风险借款对有效集的影响
1、允许无风险借款下的投资组合
在推导马科维茨有效集的过程中,我们假定投资者可 以购买风险资产的金额仅限于他期初的财富。然而,在 现实生活中,投资者可以借入资金并用于购买风险资产。 由于借款必须支付利息,而利率是已知的,在该借款 本息偿还上不存在不确定性。因此我们把这种借款称为 无风险借款。
iff i
x ,其中 [ 0 , ] p i i p i
x x 1 ,其中 x x [ 0 , 1 ] f i f, i
③
②
8
该组合的预期收益率和标准差的关系为:
p R ( 1 ) r p f
i
p R i i
y f ( x ) b k x
2
一、CAPM模型的基本假设
1.存在着大量投资者,每个投资者的财富相对于所有投 资者的财富总和来说是微不足道的。
资本资产定价模型CAPM.pptx
0.0205
14.3%
债券基金
回报率 离标差准平差方
17%
1.00%
7%
0.00%
-3%
1.00%
7.00%
0.0067
8.2%
14.3% 0.0205
9
第10页/共73页
协方差
衡量资产同步变动的程度
考虑如下的乘积:
[r股票(s)-E(r股票)][r债券(s)-E(r债券)]
协方差的定义
Cov(r股票,r债券) = S P(s)[r股票(s)-E(r股票)][r债券(s)-E(r债
26
第27页/共73页
10.4 两个资产的有效集
股票在组合的比率
0% 5% 10% 15% 20% 25% 30% 35% 40% 45% 50.00% 55% 60% 65% 70% 75% 80% 85% 90% 95% 100%
风险
8.2% 7.0% 5.9% 4.8% 3.7% 2.6% 1.4% 0.4% 0.9% 2.0% 3.08% 4.2% 5.3% 6.4% 7.6% 8.7% 9.8% 10.9% 12.1% 13.2% 14.3%
0.00%
-3%
1.00%
7.00%
0.0067
8.2%
2.05% 1 (3.24% 0.01% 2.89%) 3
8
第9页/共73页
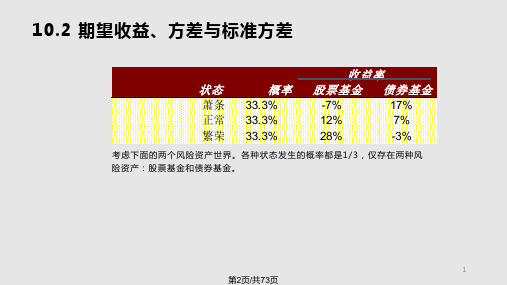
10.2 期望收益、方差与标准方差
状态
萧条 正常 繁荣
期望收益 方差 标准差
股票基金
回报率 离标差准平差方
-7%
3.24%
12%
0.01%
28%
2.89%
11.00%
24
第25页/共73页
资本资产定价模型(PPT 81张)

二、因素模型
2.3、单因素模型的常用形式: 如果CAPM成立,而且指数所代表的组合刚 i 好是市场组合,则 不应当显著区别于0;
R e i i iR m i
也被称为Jensen指数(或者Jensen’s Alpha),代表了投资的超额收益率,与夏普 比率同为评价投资基金或策略的重要指标。
2.2、单因素模型与CAPM的关系: (1)CAPM是基于事前视角的均衡模型,而 因素模型是基于事后视角的模型,可以不考 虑市场均衡; (2)CAPM可以看作一类特殊的单因素模型; (3)CAPM中所用预期收益率不可观测,因 素模型为真实收益率,可观测。
二、因素模型
2.2、单因素模型与CAPM的关系: 如果只有一种系统性风险,即市场组合代表 的风险,则根据CAPM有
例如:通货膨胀对黄金生产企业、出口导 向企业、销售商有着不同的影响
二、因素模型
2.1、单因素模型 单因素模型回报率
风险
r E r me i i i i
2 i 2 2 i m 2 e
2 ij i j m
不同证券收益率之间的协方差
二、因素模型
Eri rf i (rm rf ) 4% 0.8 (10% 4%) 4% 4.8% 8.8%
二、因素模型
2.1、单因素模型 实现的收益率总是可以划分为期望部分和 非期望之和
r i Er i u i
将实现的不确定性划分为系统性风险和特 异性风险
大 纲
第二部分:因素模型与套利定价理论(APT) 1、单因素模型 2、多因素模型 3、套利定价(APT)模型 第三部分:理论应用 1、投资衡量 2、项目成本核算 3、监管核算
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2. Mean-variance optimization with unlimited borrowing and lending at a risk-free rate
Sharpe ratio of H < Sharpe ratio of M
The combination of risk-free asset and M dominates the combination
Debt 8% 12%
Equity 13% 20%
When ρDE = -1,
wE
D D
E
1 wD
When ρDE = 0,
Bodie et al. (2014), Table 7.3, p. 211
Dr Ekaterina Svetlova
1. Brief revision: Lecture 2
Source: Bodie et al. 2014: p. 220
Dr Ekaterina Svetlova
1. Brief revision: Lecture 2
Diversifiable (non systematic) risk vs undiversifiable (systematic) risk
We construct risky portfolios varying xD and xE
to provide the lowest possible risk for any given level of expected return
E(rp) = wD E(rD) + wEE(rE)
2 p
of risk-free asset and H
Source: Perold 2004
Dr Ekaterina Svetlova
2. Mean-variance optimization with unlimited borrowing and lending at a risk-free rate
Harold J. Bowen III
Dr Ekaterina Svetlova
2. Mean-variance optimization with unlimited borrowing and lending at a risk-free rate
Dr Ekaterina Svetlova
2. Mean-variance optimization with unlimited borrowing and lending at a risk-free rate
- Standard deviation of the return: σ = 0
Dr Ekaterina Svetlova
2. Mean-variance optimization with unlimited borrowing and lending at a risk-free rate
If you invest in asset H and riskless asset: xH and xf = 1 - xH
Trustees
the Tampa firefighters and police officers pension fund
The Investment Management Firm
Investment consultants
As for being diversified, which is the mantra of nearly all institutional money managers and consultants, [the Tampa fund] isn’t. … [T]he fund’s assets are concentrated in a relatively small number of stocks and fixed-income investments. In short, the Tampa pension fund pretty much breaks all the conventional rules of fund management.
Tobin separation theorem:
Portfolio choice problem can be separated in two tasks: 1. Identify the optimal risky portfolio 2. Identify the capital allocation between
zero
Sharpe ratio: 0.305 (higher than 0.25 for M and 0.175 for H) All investors will hold assets M and H in proportions 74/26 Source: Perold 2004
Dr Ekaterina Svetlova
ErH - Rf
σH
Sharpe ratio
Dr Ekaterina Svetlova
Source: Perold 2004
(ErH - Rf)
Risk premium
2. Mean-variance optimization with unlimited borrowing and lending at a risk-free rate
Unlimited borrowing and lending at a risk-free rate:
- Riskless asset is an asset with a certain return for the given time horizon.
- For example: US Treasury bonds that automatically adjust for inflation (TIPS: Treasury inflation protected securities) or short term US Treasury bills (US T-bills)
Foundations of Financial Analysis and
Investments
Lecture 3: Capital Asset Pricing Model (CAPM)
Dr Ekaterina Svetlova
Today‘s lecture
1. Brief revision: Lecture 2 2. Mean-variance optimization with unlimited
Sharpe ratio of asset H:
Sharpe ratio of asset M:
(12% - 5%)/ 40% = 0.175
(10% - 5%)/ 20% = 0.25
Important: all combinations of asset H with risk-free borrowing and
2. Mean-variance optimization with unlimited borrowing and lending at a risk-free rate
Combining equations for portfolio return and risk, we obtain :
Erp = Rf
How much of each risky asset should one hold in the portfolio?
New efficiency line when risk-free lending/borrowing is allowed
Correlation between M and H assumed to be
1. Brief revision: Lecture 2
Expected return E(r) Standard deviation
Bodie et al. (2014), Table 7.1, p. 208
Debt 8% 12%
Equity 13% 20%
B A
Bodie et al. (2014), Table 7.3, p. 211
3. Mean-variance optimization with unlimited borrowing and lending at a risk-free rate
In case of many risky assets:
Risk aversion
Risk seeking
Source: Perold 2004
Dr Ekaterina Svetlova
1. Brief revision: Lecture 2
The portfolio consists of two risky assets D (debt) and E (equity)
Their weights in the portfolio are xD and xE (xD + xE = 1; xD ≥ 0, xE ≥ 0)
wD2
2 D
wE2
2 E
2wD wE Cov
rD , rE
Cov(rD,rE) = DEDE
Success of diversification depends on the correlation coefficient
Dr Ekaterina Svetlova
Bodie et al. 2014, Ch. 7
Erp = (1 - xH) Rf + xH RH = Rf + xH(ErH - Rf) σp = (1 - xH)2 σf + xH2 σH2 + 2xH (1 - xH) ρfH σf σH As σf = 0, we obtain:
