全等三角形证明题练习(提高题)
(完整)全等三角形证明之能力拔高(经典题目)
全等三角形能力拔高题姓名：一、角度转化问题1．已知：如图，AB⊥AE，AD⊥AC，∠E＝∠B，DE＝CB．求证：AD＝AC．2．已知：如图，AD＝AE，AB＝AC，∠DAE＝∠BAC．求证：BD＝CE．3．已知：如图，在△MPN中，H是高MQ和NR的交点，且MQ＝NQ．求证：HN＝PM.4.如图，在△ABC中，∠ACB＝90°，AC＝BC，直线l经过顶点C，过A、B两点分别作l 的垂线AE、BF，E、F为垂足．当直线l不与底边AB相交时，求证：EF＝AE＋BF．5．已知：如图，AE⊥AB，BC⊥AB，AE＝AB，ED＝AC．求证：ED⊥AC．二、二次全等问题1.已知：如图，线段AC、BD交于O，∠AOB为钝角，AB＝CD，BF⊥AC于F，DE⊥AC于E，AE＝CF．求证：BO＝DO．2．已知：如图，AC与BD交于O点，AB∥DC，AB＝DC．若过O点作直线l，分别交AB、DC于E、F两点，求证：OE＝OF.3．如图，E在AB上，∠1＝∠2，∠3＝∠4，那么AC等于AD吗？为什么？4．已知：如图，DE⊥AC，BF⊥AC，AD＝BC，DE＝BF.求证：AB∥DC.MF E CBA5、已知：如图，AD 平分∠BAC ，DE ⊥AB 于E ，DF ⊥AC 于F ，DB=DC ， 求证：EB=FC【练习】1、已知∠B=∠E=90°，CE=CB ，AB ∥CD. 求证：△ADC 是等腰三角形。
2、如图：AB=AC ，ME ⊥AB ，MF ⊥AC ，垂足分别为E 、F ，ME=MF 。
求证：MB=MCG FEDC BA3、已知，△ABC 和△ECD 都是等边三角形，且点B ，C ，D 在一条直线上求证：BE=AD4、如图：在△ABC 中，∠C =90°，AD 平分∠ BAC ，DE ⊥AB 交AB 于E ，BC=30， BD ：CD=3：2，则DE= 。
5、如图，已知，EG ∥AF ，请你从下面三个条件中，再选出两个作为已知条件，另一个作为结论，推出一个正确的命题。
人教版初二数学上册：全等三角形判定一(SSS,SAS)(提高)巩固练习
【巩固练习】一、选择题1. 如图，已知AB ＝AC ，D 为BC 的中点，结论：①AD ⊥BC ；②AD 平分∠BAC ；③∠B ＝∠C ；④△ABC 是等边三角形.其中正确的是（ ）.A.①②B. ②③C. ①②③D. ③④2．如图，AD 是ABC ∆的中线，E 、F 分别是AD 和AD 延长线上的点，且DE DF =，连接BF 、CE ，下列说法：①CE BF =；② ABD ∆和ACD ∆的面积相等；③//BF CE ；④ BDF ∆≌CDE ∆，其中正确的有（ ）．A.1个B.2个C.3个D.4个3. AD 为△ABC 中BC 边上的中线, 若AB ＝2, AC ＝4, 则AD 的范围是( )A .AD ＜6 B. AD ＞2 C. 2＜AD ＜6 D. 1＜AD ＜34．（2015•杭州模拟）用直尺和圆规作已知角的平分线的示意图如下，则说明∠CAD=∠DAB的依据是（ ）A ．SSSB ． SASC ． ASAD ． AAS5. 根据下列条件能唯一画出△ABC 的是（ ）A.AB ＝3，BC ＝4，AC ＝8B.AB ＝4，BC ＝3，∠A ＝30°C.AB ＝5，AC ＝6，∠A ＝45°D. ∠A ＝30°，∠B ＝60°，∠C ＝90°6.（2016•洛阳模拟）已知：如图，在长方形ABCD 中，AB=4，AD=6．延长BC 到点E ，使CE=2，连接DE ，动点P 从点B 出发，以每秒2个单位的速度沿BC ﹣CD ﹣DA 向终点A运动，设点P 的运动时间为t 秒，当t 的值为（ ）秒时，△ABP 和△DCE 全等．A．1 B．1或3 C．1或7 D．3或7二、填空题7. 如图，AB＝CD，AC＝DB，∠ABD＝25°，∠AOB＝82°，则∠DCB＝_________.8. 如图，△ABC是三边均不等的三角形，DE＝BC，以D、E为两个顶点画位置不同的三角形，使所作的三角形与△ABC全等，这样的三角形最多可以画个.9. （2016•微山县二模）如图，四边形ABCD中，∠1=∠2，请你补充一个条件，使△ABC≌△CDA．10.（2014春•鹤岗校级期末）如图：在△ABC和△FED中，AD=FC，AB=FE，当添加条件____________时，就可得到△ABC≌△FED．（只需填写一个即可）11. 如图所示，BE⊥AC于点D，且AD＝CD，BD＝ED，若∠ABC＝54°，则∠E＝°.AA BB的中点连在一起，可以做成一个测量工件内槽宽的工具（卡钳），12. 把两根钢条','如图，若测得AB＝5厘米，则槽宽为厘米．三、解答题13.（2014秋•天津期末）如图在△ABE中，已知AB=AE，AD=AC，∠1=∠2．求证：△ABC≌△AED．14. 如图, ∠B＝∠C, BD＝CE, CD＝BF.求证: ∠EDF ＝ 90︒－12∠A15. 已知：如图，BE、CF是△ABC的高，且BP＝AC，CQ＝AB，求证：AP⊥AQ.【答案与解析】一.选择题1. 【答案】C【解析】由SSS证全等可得①②③是正确的.2. 【答案】D；3. 【答案】D；【解析】用倍长中线法；4. 【答案】A；【解析】解：从角平分线的作法得出，△AFD 与△AED 的三边全部相等，则△AFD≌△AED．故选A ．5. 【答案】C ；【解析】A 不能构成三角形，B 没有SSA 定理，D 没有AAA 定理.6. 【答案】C ；【解析】解：因为AB=CD ，若∠ABP=∠DCE=90°，BP=CE=2，根据SAS 证得△ABP ≌△DCE ，由题意得：BP=2t=2，所以t=1，因为AB=CD ，若∠BAP=∠DCE=90°，AP=CE=2，根据SAS 证得△BAP ≌△DCE ，由题意得：AP=16﹣2t=2，解得t=7．所以，当t 的值为1或7秒时．△ABP 和△DCE 全等． 故选C ．二.填空题7. 【答案】66°；【解析】可由SSS 证明△ABC ≌△DCB ，∠OBC ＝∠OCB ＝82412︒=︒，所以∠DCB ＝ ∠ABC ＝25°＋41°＝66°8. 【答案】4；【解析】在DE 的两侧可以各画2个.9.【答案】AD=BC ；【解析】由题意知，已知条件是△ABC 与△CDA 对应角∠1=∠2、公共边AC=CA ，所以根据全等三角形的判定定理SAS 来证△ABC ≌△CDA 时，需要添加的条件是AD=BC.10.【答案】BC=ED 或∠A=∠F .11.【答案】27；【解析】可证△ADB ≌△CDB ≌△CDE.12.【答案】5；三.解答题13.【解析】证明：∵∠1=∠2，∴∠1+∠DAC=∠2+∠DAC ，∴∠BAC=∠EAD ，在△ABC 和△AED 中，，∴△ABC ≌△AED （SAS ）．14.【解析】证明：在△ABC 中，∠B ＝∠C ，∴∠B ＝90︒-12∠A 在△DBF 和△ECD 中BD CE B C BF CD =⎧⎪∠=∠⎨⎪=⎩∴△DBF ≌△ECD （SAS ）∴∠BFD ＝∠CDE∴∠EDF ＝180°－∠BDF －∠CDE ＝180°－（∠BDF ＋∠BFD ）＝∠B ＝90︒－12∠A .15.【解析】证明：∵BE ⊥AC ，CF ⊥AB （已知）∴∠ACF ＋∠BAC ＝90°，∠ABE ＋∠BAC ＝90°，（三角形内角和定理）∠ACF ＝∠ABE （等式性质）在△ACQ 和△PBA 中 ∵⎪⎩⎪⎨⎧=∠=∠=BP AC ABP ACF AB CQ∴△ACQ ≌△PBA （SAS ）∴∠Q ＝∠BAP （全等三角形对应角相等）∵CF ⊥AB （已知）∴∠Q ＋∠QAF ＝90°，（垂直定义）∴∠BAP ＋∠QAF ＝90°，（等量代换）∴AP ⊥AQ.（垂直定义）附录资料：【巩固练习】一、选择题1. （2016•长沙模拟） 如图所示，△ABC ≌△DEC ，则不能得到的结论是（ ）A. AB ＝DEB. ∠A ＝∠DC. BC ＝CDD. ∠ACD ＝∠BCE2. 如图，△ABC ≌△BAD ，A 和B ，C 和D 分别是对应顶点，若AB ＝6cm ，AC ＝4cm ，BC ＝5cm ，则AD 的长为（ ）A. 4cmB. 5cmC. 6cmD. 以上都不对3. 下列说法中正确的有（ ）①形状相同的两个图形是全等图形 ②对应角相等的两个三角形是全等三角形 ③全等三角形的面积相等 ④若△ABC ≌△DEF ，△DEF ≌△MNP ，△ABC ≌△MNP.A.0个B.1个C.2个D.3个4. （2014秋•庆阳期末）如图，△ABC ≌△A ′B ′C ，∠ACB=90°，∠A ′CB=20°，则∠BCB ′的度数为（）A.20°B.40°C.70°D.90°5. 已知△ABC≌△DEF，BC＝EF＝6cm，△ABC的面积为18平方厘米，则EF边上的高是（）A.6cmB.7cmC.8cmD.9cm6. 将一张长方形纸片按如图所示的方式折叠，BC、BD分别为折痕，则∠CBD的度数为（）A．60° B．75°C．90°D．95°二、填空题7.（2014秋•安阳县校级期末）如图所示，△AOB≌△COD，∠AOB=∠COD，∠A=∠C，则∠D的对应角是___________，图中相等的线段有____________________________．8. （2016•成都）如图，△ABC≌△A′B′C′，其中∠A=36°，∠C′=24°，则∠B=___________.9. 已知△DEF≌△ABC，AB＝AC，且△ABC的周长为23cm，BC＝4cm，则△DEF的边中必有一条边等于______.10. 如图，如果将△ABC向右平移CF的长度，则与△DEF重合，那么图中相等的线段有__________；若∠A＝46°，则∠D＝________.11.已知△ABC ≌△'''A B C ，若△ABC 的面积为10 2cm ，则△'''A B C 的面积为________ 2cm ，若△'''A B C 的周长为16cm ，则△ABC 的周长为________cm ．12. △ABC 中，∠A ∶∠C ∶∠B ＝4∶3∶2，且△ABC ≌△DEF ，则∠DEF ＝______ .三、解答题13.如图，已知△ABC ≌△DEF ，∠A ＝30°，∠B ＝50°，BF ＝2，求∠DFE 的度数与EC 的长.14. （2014秋•射阳县校级月考）如图，在图中的两个三角形是全等三角形，其中A 和D 、B 和E 是对应点．（1）用符号“≌“表示这两个三角形全等（要求对应顶点写在对应位置上）；（2）写出图中相等的线段和相等的角；（3）写出图中互相平行的线段，并说明理由．15. 如图，E 为线段BC 上一点，AB ⊥BC ，△ABE ≌△ECD.判断AE 与DE 的关系，并证明你的结论.【答案与解析】一.选择题1. 【答案】C ；【解析】因为△ABC ≌△DEC ，可得：AB=DE ，∠A=∠D ，BC=EC ，∠ACD=∠BCE ，故选C ．2. 【答案】B ；【解析】AD与BC是对应边，全等三角形对应边相等.3. 【答案】C；【解析】③和④是正确的；4. 【答案】C；【解析】解：∵△ACB≌△A′CB′，∴∠ACB=∠A′CB′，∴∠BCB′=∠A′CB′﹣∠A′CB=70°．故选C．5. 【答案】A；【解析】EF边上的高＝1826 6⨯=；6. 【答案】C；【解析】折叠所成的两个三角形全等，找到对应角可解.二.填空题7. 【答案】∠OBA，OA=OC、OB=OD、AB=CD；【解析】解：∵△AOB≌△COD，∠AOB=∠COD，∠A=∠C，∴∠D=∠OBA，OA=OC、OB=OD、AB=CD，故答案为：∠OBA，OA=OC、OB=OD、AB=CD．8. 【答案】120°；【解析】∵△ABC≌△A′B′C′，∴∠C=∠C′=24°，∴∠B=180°﹣∠A﹣∠B=120°．9. 【答案】4cm或9.5cm；【解析】DE＝DF＝9.5cm，EF＝4cm；10.【答案】AB＝DE、AC＝DF、BC＝EF、BE＝CF， 46°；11.【答案】10，16；【解析】全等三角形面积相等，周长相等；12.【答案】40°；【解析】见“比例”设k，用三角形内角和为180°求解.三.解答题13.【解析】解：在△ABC中，∠ACB＝180°－∠A－∠B，又∠A＝30°，∠B＝50°，所以∠ACB＝100°.又因为△ABC≌△DEF，所以∠ACB＝∠DFE，BC＝EF（全等三角形对应角相等，对应边相等）所以∠DFE＝100°EC＝EF－FC＝BC－FC＝BF＝2.14. 【解析】解：（1）△ABC≌△DEF；（2）AB=DE，BC=EF，AC=DF；∠A=∠D，∠B=∠E，∠ACB=∠DFE；（3）BC∥EF，AB∥DE，理由是：∵△ABC≌△DEF，∴∠A=∠D，∠ACB=∠DFE，∴AB∥DE，BC∥EF．15. 【解析】 AE＝DE ,且AE⊥DE证明：∵△ABE≌△ECD，∴∠B＝∠C，∠A＝∠DEC，∠AEB＝∠D，AE＝DE又∵AB⊥BC∴∠A＋∠AEB＝90°，即∠DEC＋∠AEB＝90°∴AE⊥DE∴AE与DE垂直且相等.。
全等三角形证明经典50题(含答案)
全等三角形证明经典50题(含答案)1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中AB-BE ＜AE ＜AB+BE ∵AB=4即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=22. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB证明：延长CD 与P ，使D 为CP 中点。
连接AP,BP ∵DP=DC,DA=DB ∴ACBP 为平行四边形 又∠ACB=90 ∴平行四边形ACBP 为矩形 ∴AB=CP=1/2ABADBCBACDF21E3.已知：BC=DE，∠B=∠E，∠C=∠D，F是CD中点，求证：∠1=∠2证明：连接BF和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴三角形BCF全等于三角形EDF(边角边)∴BF=EF,∠CBF=∠DEF连接BE在三角形BEF中,BF=EF∴∠EBF=∠BEF。
∵∠ABC=∠AED。
∴∠ABE=∠AEB。
∴AB=AE。
在三角形ABF和三角形AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴三角形ABF和三角形AEF全等。
∴∠BAF=∠EAF (∠1=∠2)。
4.已知：∠1=∠2，CD=DE，EF//AB，求证：EF=AC证明：过C作CG∥EF交AD的延长线于点GCG∥EF，可得，∠EFD＝CGDDE＝DC∠FDE＝∠GDC（对顶角）∴△EFD≌△CGDEF＝CG∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC5.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠C证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE上取F，使EF＝EB，连接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF，CE＝CE，∴△CEB≌△CEF∴∠B＝∠CFE∵∠B＋∠D＝180°，∠CFE＋∠CFA＝180°∴∠D＝∠CFA∵AC平分∠BAD∴∠DAC＝∠FAC∵AC＝AC∴△ADC≌△AFC（SAS）∴AD＝AF∴AE＝AF＋FE＝AD＋BEA7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD8. 已知：D 是AB 中点，∠ACB=90°，求证：1CD AB9. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。
全等三角形判定二(SSS,AAS)(提高)巩固练习
【巩固练习】一、选择题1．如图，∠A＝∠D，∠B＝∠E，BF＝CE，下列结论错误的是（）A.△ABC≌△DEFB. BF＝ECC.AC∥DED.AC＝DF2．如图，AB∥EF，DE∥AC，BD＝CF，则图中不是全等三角形的是（）A.△BAC≌FEDB. △BDA≌FCEC. △DEC≌CADD. △BAC≌FCE3．如图，AB＝BD，∠1＝∠2，要用AAS判定△ABC≌△DBE，则添加的条件是（） A.AE＝EC B.∠D＝∠A C.BE＝BC D.∠DEB＝∠C4．下列判断中错误的是（）A.有两角和一边对应相等的两个三角形全等B.有两边和一角对应相等的两个三角形全等C.有两边和其中一边上的中线对应相等的两个三角形全等D.有一边对应相等的两个等边三角形全等5．（•滕州市校级模拟）如图，在下列条件中，不能证明△ABD≌△ACD的是（）A．BD=DC，AB=AC B．∠ADB=∠ADC，BD=DCC．∠B=∠C，∠BAD=∠CAD D．∠B=∠C，BD=DC6．如图，点A在DE上，AC＝CE，∠1＝∠2＝∠3，则DE的长等于（）A．DC B．BC C．AB D．AE＋AC二、填空题7．（春•鹤岗校级期末）如图：在△ABC和△FED中，AD=FC，AB=FE，当添加条件________________时，就可得到△ABC≌△FED．（只需填写一个即可）8．如图，点D在AB上，点E在AC上，且∠B＝∠C，在条件①A B＝AC，②AD＝AE，③BE＝CD，④∠AEB＝∠ADC中，不能使△ABE≌△ACD的是_______.（填序号）9．已知，如图，AB∥CD，AF∥DE，AF＝DE，且BE＝2，BC＝10，则EF＝________. 10．如图，AB∥CD，AD∥BC，OE＝OF，图中全等三角形共有______对.11．如图，直线l过正方形ABCD的顶点B，点A、C到直线l的距离分别是1和2，则EF 的长是___________．12．在△ABC 和△DEF 中（1）AB ＝DE ；（2）BC ＝EF ；（3）AC ＝DF ；（4）∠A＝∠D；（5）∠B＝∠E；（6）∠C＝∠F 从这六个条件中选取三个条件可判定△ABC 与△DEF 全等的方法共有________种.三、解答题13．（2014秋•景洪市校级期中）如图，O 为码头，A ，B 两个灯塔与码头的距离相等，OA ，OB 为海岸线，一轮船离开码头，计划沿∠AOB 的平分线航行，在航行途中，测得轮船与灯塔A 和灯塔B 的距离相等，试问轮船航行时是否偏离预定航线，请说明理由．14．已知：如图，ABC △中，45ABC ∠=°，CD AB ⊥于D ，BE AC ⊥于E ，BE 与CD 相交于点F ．求证：BF AC =.15． 如图，DC∥AB，∠BAD 和∠ADC 的角平分线相交于E ，过E 的直线分别交DC 、AB 于C 、B 两点.求证：AD ＝AB ＋DC.【答案与解析】一、选择题1．【答案】C ；2．【答案】D ；3．【答案】D ；【解析】满足判定定理AAS 的只有D 选项.4．【答案】B ；【解析】C 选项和D 选项都可以由SSS 定理证全等.5．【答案】D ；【解析】解：A、∵在△ABD和△ACD中，∴△ABD≌△ACD（SSS），故本选项错误；B、∵在△ABD和△ACD中，∴△ABD≌△ACD（SAS），故本选项错误；C、∵在△ABD和△ACD中，∴△ABD≌△ACD（AAS），故本选项错误；D、不符合全等三角形的判定定理，不能推出△ABD≌△ACD，故本选项正确；故选D．6．【答案】C；【解析】可证∠BAC＝∠E，∠BCA＝∠DCE，所以△ABC≌△EDC，DE＝AB.二、填空题7．【答案】BC=ED.8．【答案】④【解析】三个角对应相等不能判定三角形全等.9．【答案】6；【解析】△ABF≌△CDE，BE＝CF＝2，EF＝10－2－2＝6.10．【答案】6；【解析】△ABO≌△CDO，△AFO≌△CEO，△DFO≌△BEO，△AOD≌△COB，△ABD≌△CDB，△ABC≌△CDA.11．【答案】3；【解析】由AAS证△ABF≌△CBE，EF＝FB＋BE＝CE＋AF＝2＋1＝3.12．【答案】13；【解析】ASA类型3种，AAS类型6种，SAS类型3种，SSS类型一种，共13种.三、解答题13．【解析】解：此时轮船没有偏离航线．理由：由题意知：假设轮船在D处，则DA=DB，AO=BO，在△ADC和△BDC中，，∴△ADO≌△BDO（SSS），∴∠AOD=∠BOD，即DO为∠AOB的角平分线，∴此时轮船没有偏离航线．14．【解析】证明： ∵ CD AB ⊥∴ 90BDC CDA ∠=∠=︒∵ 45ABC ∠=︒∴ 45DCB ABC ∠=∠=︒∴ DB DC =∵ BE AC ⊥∴ 90AEB ∠=︒∴ 90A ABE ∠+∠=︒∵ 90CDA ∠=︒∴ 90A ACD ∠+∠=︒∴ ABE ACD ∠=∠在BDF ∆和CDA ∆中BDC CDA DB DCABE ACD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴BDF ∆≌CDA ∆（AAS ）∴BF AC =.15．【解析】证明：延长DE 交AB 的延长线于F∴∠CDE＝∠F, ∠CDA＋∠BAD＝180º∵DE 平分∠CDA,AE 平分∠DAB ∴∠CDE＝∠ADE＝21∠CDA, ∠DAE＝∠EAF＝21∠BAD ∴∠ADE＝∠F,∠E DA ＋∠DAE＝90º∴∠AED＝∠AEF＝90º在△ADE 与△AFE 中 ⎪⎩⎪⎨⎧=∠=∠∠=∠AE AE FEA DEA F ADE∴△ADE≌△AFE （AAS ）∴DE＝EF,AD ＝AF在△DCE 与△FBE 中， FE D CB A⎪⎩⎪⎨⎧∠=∠=∠=∠FEB DEC FEDE F CDE ∴△DCE≌△FBE（ASA ）∴DC＝BF ，∴AD＝AB ＋DC.。
全等三角形提高32题(含答案)
全等三角形提高32题（含答案）（一）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD2. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠23. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC4. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C5. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE6. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。
求证：BC=AB+DC 。
C D B AB C D EF 21 AD B CAB ACDF2E7. 已知：AB//ED ，∠EAB=∠BDE ，AF=CD ，EF=BC ，求证：∠F=∠C8．如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ．9．如图，OM 平分∠POQ ，MA ⊥OP ,MB⊥OQ ，A 、B 为垂足，AB 交OM 于点N ．求证：∠OAB =∠OBA10．如图，已知AD ∥BC ，∠PAB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP于D ．求证：AD +BC =AB ．11．如图，△ABC 中，AD 是∠CAB 的平分线，且AB =AC +CD ，求证：∠C =2∠B12．如图①，E 、F 分别为线段AC 上的两个动点，且DE ⊥AC 于E ，BF ⊥AC 于F ，若AB =CD ，AF =CE ，BD 交AC 于点M ．（1）求证：MB =MD ，ME =MF（2）当E 、F 两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由． D C B A F E PED C B AD C B A13．已知：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点，（1）求证：△AED ≌△EBC ．（2）观看图前，在不添辅助线的情况下，除△EBC外，请再写出两个与△AED 的面积相等的三角形．（直接写出结果，不要求证明）：14．如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ．求证：BD =2CE ． 15、如图：AE 、BC 交于点M ，F 点在AM 上，BE ∥CF ，BE=CF 。
全等三角形证明经典50题(含答案)
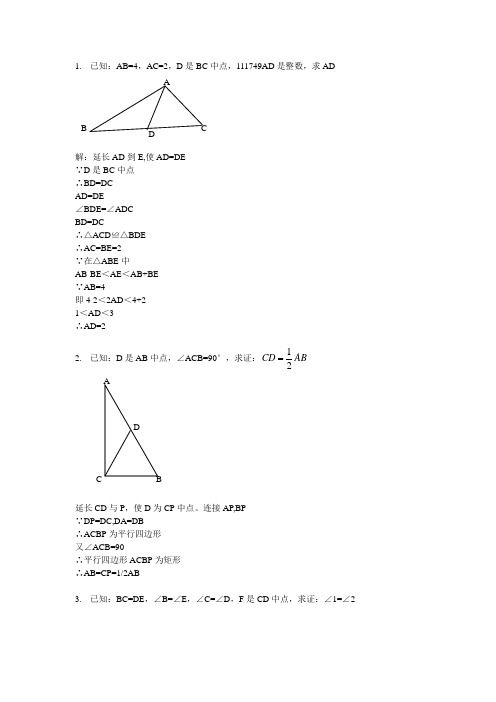
1. 已知：AB=4，AC=2，D 是BC 中点，111749AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DCAD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=22. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB延长CD 与P ，使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2AD BC证明：连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ，可得，∠EFD ＝CGDDE ＝DC∠FDE ＝∠GDC （对顶角）∴△EFD ≌△CGDEF ＝CGBACDF21 E∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC5.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠CA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF∵CE ⊥AB∴∠CEB ＝∠CEF ＝90°∵EB ＝EF ，CE ＝CE ，∴△CEB ≌△CEF∴∠B ＝∠CFE∵∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180°∴∠D ＝∠CFA∵AC 平分∠BAD∴∠DAC ＝∠FAC∵AC ＝AC∴△ADC ≌△AFC （SAS ）∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE＜AE＜AB+BE ∵AB=4即4-2＜2AD＜4+21＜AD＜3∴AD=28.已知：D是AB中点，∠ACB=90°，求证：12 CD AB9.已知：BC=DE，∠B=∠E，∠C=∠D，F是CD中点，求证：∠1=∠2证明：连接BF 和EF 。
全等三角形证明题及答案(15道)
全等三角形的判定与性质．
7.如图，D、E分别是AB、AC上的点，且 AB=AC，AD=AE．求证：∠B=∠C．
在△ABE和△ACD中， ∵ AB=AC ∠A=∠A AE=AD ， ∴△ABE≌△ACD〔SAS〕， ∴∠B=∠C．
证明：∵AB∥DE， ∴∠B=∠DEF． ∵BE=CF， ∴BC=EF． ∵∠ACB=∠F， ∴ ∠B=∠DEF BC=EF∠ACB=∠F ， ∴△ABC≌△DEF．
全等三角形的判定；平行线的性质．
10.：如图，E、F在AC上，AD∥CB且AD=CB，∠D=∠B． 求证：AE=CF．
证明：∵AD∥CB， ∴∠A=∠C， 在△ADF和△CBE中， ∠A=∠C AD=CB ∠D=∠B ， ∴△ADF≌△CBE〔ASA〕， ∴AF=CE， ∴AF+EF=CE+EF，即AE=CF．
∴△BCF≌△CBD〔ASA〕． 全等三角形的判定．
如图，在△ABC中，D是BC的中点，DE⊥AB， DF⊥AC，垂足分别是E，F，BE=CF． 求证：AD是△ABC的角平分线．
证明：∵DE⊥AB，DF⊥AC， ∴Rt△BDE=Rt△DCF=90°． BD=DC BE=CF ， ∴Rt△BDE≌Rt△DCF〔HL〕， ∴DE=DF， 又∵DE⊥AB，DF⊥AC， ∴AD是角平分线．
系和位置关系？并加以证明．
• 证明：∵AB∥CD， • ∴∠A=∠D， • ∵在△ABF和△DCE中 • AB=CD ∠A=∠D
AF=DE ， • ∴△ABF≌△DCE， • ∴CE=BF，
直角三角形全等的证明及三角形全等提高题
7.如图，在△ABC中，已知D是BC中点，DE⊥AB，DF⊥AC，垂足分别是E、F，DE＝DF. 求证：AB=AC8.已知：如图，AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC＝DC.你能说明BE与DF相等吗？9．已知：如图，在△ABC中，∠ACB=90°，CD⊥AB于D，∠A=30°.求证:BD=14ABCDF12AB10.如图，在△ABC 中，AB =AC ，DE 是过点A 的直线，BD ⊥DE 于D ，CE ⊥DE 于E ． （1）若BC 在DE 的同侧（如图①）且AD =CE ，说明：BA ⊥A C ．（2）若BC 在DE 的两侧（如图②）其他条件不变，问AB 与AC 仍垂直吗？若是请予证明，若不是请说明理由．1已知：如图，四边形ABCD 中，AC 平分角BAD ，CE 垂直AB 于E ，且角B+角D=180度，求证：AE=AD+BEAB DCE122已知，如图，AB=CD ，DF ⊥AC 于F ，BE ⊥AC 于E ，DF=BE 。
求证：AF=CE 。
3已知，如图，AB ⊥AC ，AB ＝AC ，AD ⊥AE ，AD ＝AE 。
求证：BE ＝CD 。
F EA C D BA ED C B4如图，DE ⊥AB ，DF ⊥AC ，垂足分别为E 、F ，请你从下面三个条件中任选出两个作为已知条件，另一个为结论，推出一个正确的命题。
① AB=AC ② BD=CD ③ BE=CF7、已知：如图，AB ⊥BC ，AD ⊥DC ，AB=AD ，若E 是AC 上一点。
求证：EB=ED 。
DA E CB8、已知：如图，AB 、CD 交于O 点，CE//DF ，CE=DF ，AE=BF 。
求证：∠ACE=∠BDF 。
9. 已知：如图，△ABC 中，AD ⊥BC 于D ，E 是AD 上一点，BE 的延长线交AC 于F ，若BD=AD ，DE=DC 。
求证：BF ⊥AC 。
10. 已知：如图，△ABC 和△A ＇B ＇C ＇中，∠BAC=∠B ＇A ＇C ＇，∠B=∠B ＇，AD 、A ＇D ＇分别是∠BAC、∠B ＇A ＇C ＇的平分线，且AD=A ＇D ＇。
(完整版)全等三角形证明经典50题(含答案)
全等三角形证明经典50题(含答案)1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD2. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠24. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠CDAB B A CDF2 1 EAC D E F 21 A D BC A6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。
求证：BC=AB+DC 。
13.已知：AB//ED ，∠EAB=∠BDE ，AF=CD ，EF=BC ，求证：∠F=∠C14. P 是∠BAC 平分线AD 上一点，AC>AB ，求证：PC-PB<AC-AB15. 已知∠ABC=3∠C ，∠1=∠2，BE ⊥AE ，求证：AC-AB=2BED C B A FE PD A CB16. 已知，E 是AB 中点，AF=BD ，BD=5，AC=7，求DC18．如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ．19．如图，OM 平分∠POQ ，MA ⊥OP ,MB ⊥OQ ，A 、B 为垂足，AB 交OM 于点N ．求证：∠OAB =∠OBA20．（5分）如图，已知AD ∥BC ，∠P AB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．21．如图，△ABC 中，AD 是∠CAB 的平分线，且AB =AC +CD ，求证：∠C =2∠B22．（6分）如图①，E 、F 分别为线段AC 上的两个动点，且DE ⊥AC 于E ，BF ⊥AC 于F ，若AB =CD ，AF =CE ，BD 交AC 于点M ．（1）求证：MB =MD ，ME =MF（2）当E 、F 两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．F AEDCB P E D CB A DC B A23．已知：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点， （1）求证：△AED ≌△EBC ． （2）观看图前，在不添辅助线的情况下，除△EBC 外，请再写出两个与△AED 的面积相等的三角形．（直接写出结果，不要求证明）：24．（7分）如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ．求证：BD =2CE ．证明：25、如图：DF=CE ，AD=BC ，∠D=∠C 。
全等三角形证明经典50题(含答案)
1. 已知：AB=4，AC=2，D 是BC 中点，111749AD 是整数，求AD解：延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4 即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=2 2. 已知：D 是AB 中点，∠ACB=90°，求证：12CD ABA DB C延长CD 与P ，使D 为CP 中点。
连接AP,BP ∵DP=DC,DA=DB ∴ACBP 为平行四边形 又∠ACB=90 ∴平行四边形ACBP 为矩形 ∴AB=CP=1/2AB 3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠24.5. 证明：连接BF 和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴三角形BCF 全等于三角形EDF(边角边)∴BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴∠EBF=∠BEF 。
C D FB C∵∠ABC=∠AED 。
∴∠ABE=∠AEB 。
∴AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴三角形ABF 和三角形AEF 全等。
∴∠BAF=∠EAF(∠1=∠2)。
6. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ，可得，∠EFD ＝CGDDE ＝DC∠FDE ＝∠GDC （对顶角）∴△EFD ≌△CGDEF ＝CG∠CGD ＝∠EFD又，EF ∥AB∴，∠EFD ＝∠1∠1=∠2∴∠CGD ＝∠2∴△AGC 为等腰三角形，AC ＝CG又EF ＝CG∴EF ＝AC7. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠CB ACDF2 1EA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD（SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C8.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE上取F，使EF＝EB，连接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF，CE＝CE，∴△CEB≌△CEF∴∠B＝∠CFE∵∠B＋∠D＝180°，∠CFE＋∠CFA＝180°∴∠D＝∠CFA∵AC平分∠BAD∴∠DAC＝∠FAC∵AC＝AC∴△ADC≌△AFC（SAS）∴AD＝AF∴AE＝AF＋FE＝AD＋BE9.已知：AB=4，AC=2，D是BC中点，AD是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4 即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=2 10. 已知：D 是AB 中点，∠ACB=90°，求证：1CD ABADB C在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE ∵AB=4 即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=2 11.已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。
(必考题)初中八年级数学上册第十二章《全等三角形》提高练习(答案解析)
一、选择题1．如图已知ABC ∆中，12AB AC cm ==，B C ∠=∠，8BC cm =，点D 为AB 的中点．如果点P 在线段BC 上以2/cm s 的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动．若点Q 的运动速度为v ，则当BPD ∆与CQP ∆全等时，v 的值为（ ）A ．1B ．3C ．1或3D ．2或3D解析：D【分析】 设运动时间为t 秒，由题目条件求出BD=12AB=6，由题意得BP=2t ，则CP=8-2t ，CQ=vt ，然后结合全等三角形的判定方法，分两种情况列方程求解．【详解】解：设运动时间为t 秒，∵12AB AC cm ==，点D 为AB 的中点．∴BD=12AB=6， 由题意得BP=2t ，则CP=8-2t ，CQ=vt ，又∵∠B=∠C∴①当BP=CQ ，BD=CP 时，BPD ∆≌CQP ∆∴2t=vt ，解得：v=2②当BP=CP ，BD=CQ 时，BPD ∆≌CPQ ∆∴8-2t=2t ，解得：t=2将t=2代入vt=6，解得：v=3综上，当v=2或3时，BPD ∆与CQP ∆全等故选：D【点睛】本题主要考查了全等三角形全等的判定、熟练掌握全等三角形的判定方法是解题的关键，学会用分类讨论的思想思考问题，属于中考常考题型．2．如图O 是ABC 内的一点，且O 到三边AB 、BC 、CA 的距离==OF OD OE ．若70A ∠=︒，则BOC ∠（ ）．A ．125°B ．135°C ．105°D ．100°A 解析：A【分析】根据到角的两边距离相等的点在角的平分线上判断出点O 是三角形三条角平分线的交点，再根据三角形的内角和定理求出∠ABC+∠ACB ，然后求出∠OBC+∠OCB ，再利用三角形的内角和定理列式计算即可得解．【详解】解：∵O 到三边AB 、BC 、CA 的距离OF=OD=OE ，∴点O 是三角形三条角平分线的交点，∵∠BAC=70°，∴∠ABC+∠ACB=180°-70°=110°，∴∠OBC+∠OCB= 12（∠ABC+∠ACB ）= 12×110°=55°， 在△OBC 中，∠BOC=180°-（∠OBC+∠OCB ）=180°-55°=125°．故选：A ．【点睛】本题考查了角平分线判定定理，三角形的内角和定理，要注意整体思想的利用． 3．如图，,AD BC ⊥垂足为,D BF AC ⊥，垂足为,F AD 与BF 交于点,5,2E AD BD DC ===，则AE 的长为（ ）A ．2B ．5C ．3D ．7C解析：C【分析】 先证明△ACD ≌△BED ，得到CD=ED=2，即可求出AE 的长度．【详解】解：∵AD BC ⊥，BF AC ⊥，∴90AFE BDE ADC ∠=∠=∠=︒，∵AEF BED ∠=∠，∴EAF EBD ∠=∠，∵5AD BD ==，∴△ACD ≌△BED ，∴CD=ED=2，∴523AE AD ED =-=-=；故选：C ．【点睛】本题考查了全等三角形的判定和性质，余角的性质，解题的关键是掌握全等三角形的判定和性质，从而进行解题．4．如图，在ABC 和AEF 中，EAC BAF ∠=∠，EA BA =，添加下面的条件：①EAF BAC ∠=∠；②E B ∠=∠；③AF AC =；④EF BC =，其中可以得到ABC AEF ≌△△的有（ ）个．A ．1B ．2C ．3D ．4B解析：B【分析】 根据EAC BAF ∠=∠，EAF EAC CAF ∠=∠+∠，BAC BAF CAF ∠=∠+∠，经推到得EAF BAC ∠=∠；再结合全等三角形判定的性质分析，即可得到答案．【详解】∵EAC BAF ∠=∠，EAF EAC CAF ∠=∠+∠，BAC BAF CAF ∠=∠+∠ ∴EAF BAC ∠=∠E B ∠=∠，即E B EAF BAC EA BA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ABC AEF ≌△△()ASA ，故②符合题意；AF AC =，即AF AC EAF BAC EA BA =⎧⎪∠=∠⎨⎪=⎩∴ABC AEF ≌△△()SAS ，故③符合题意；①和④不构成三角形全等的条件，故错误；故选：B ．【点睛】本题考查了全等三角形的知识；解题的关键是熟练掌握全等三角形的性质，从而完成求解．5．如图所示，已知AB ∥CD ，BAC ∠与ACD ∠的平分线交于点O ，OE AC ⊥于点E ，且3OE cm =，则点O 到AB ，CD 的距离之和是（ ）A．3cm B．6cm C．9cm D．12cm B解析：B【分析】过点O作MN，MN⊥AB于M，证明MN⊥CD，则MN的长度是AB和CD之间的距离；然后根据角平分线的性质，分别求出OM、ON的长度，再把它们求和即可．【详解】如图，过点O作MN，MN⊥AB于M，交CD于N，∵AB∥CD，∴MN⊥CD，∵AO是∠BAC的平分线，OM⊥AB，OE⊥AC，OE＝3cm，∴OM＝OE＝3cm，∵CO是∠ACD的平分线，OE⊥AC，ON⊥CD，∴ON＝OE＝3cm，∴MN＝OM＋ON＝6cm，即AB与CD之间的距离是6cm，故选B【点睛】此题主要考查角平分线的性质和平行线之间的距离，解答此题的关键是要明确：①角的平分线上的点到角的两边的距离相等，②从一条平行线上的任意一点到另一条直线作垂线，垂线段的长度叫两条平行线之间的距离，③平行线间的距离处处相等．6．如图所示，下面甲、乙、丙三个三角形和ABC全等的图形是（）A ．甲和乙B ．乙和丙C ．只有丙D ．只有乙B解析：B【分析】 甲只有2个已知条件，缺少判定依据；乙可根据SAS 判定与△ABC 全等；丙可根据AAS 判定与△ABC 全等，可得答案．【详解】解：甲三角形只知道两条边长无法判断是否与△ABC 全等；乙三角形夹50°内角的两边分别与已知三角形对应相等，故乙与△ABC 全等；丙三角形72°内角及所对边与△ABC 对应相等且均有50°内角，可根据AAS 判定乙与△ABC 全等；则与△ABC 全等的有乙和丙，故选：B ．【点睛】本题主要考查全等三角形的判定定理，熟练掌握并充分理解三角形全等的判定定理，注意对应二字的理解很重要．7．用三角尺画角平分线：如图，先在AOB ∠的两边分别取OM ON =，再分别过点M ，N 作OA ，OB 的垂线，交点为P ．得到OP 平分AOB ∠的依据是（ ）A ．HLB ．SSSC ．SASD ．ASA A解析：A【分析】 利用垂直得到90PMO PNO ∠=∠=，再由OM ON =，OP OP =即可根据HL 证明()HL ≌PMO PNO △△，由此得到答案.【详解】∵PM OA ⊥，PN OB ⊥，∴90PMO PNO ∠=∠=．∵OM ON =，OP OP =，∴()HL ≌PMO PNO △△， ∴POA POB ∠=∠，故选：A ．【点睛】此题考查三角形全等的判定定理：SSS 、SAS 、ASA 、AAS 、HL ，根据题中的已知条件确定对应相等的边或角，由此利用以上五种方法中的任意一种证明两个三角形全等.8．如图，AB 与CD 相交于点E ，AD=CB ，要使△ADE ≌△CBE ，需添加一个条件，则添加的条件以及相应的判定定理正确的是（ ）A ．AE=CE ；SASB ．DE=BE ；SASC ．∠D=∠B ；AASD ．∠A=∠C ；ASA C解析：C【分析】 根据三角形全等的判定方法结合全等的判定方法逐一进行来判断．【详解】解：A.添加AE=CE 后，根据已知两边和其中一边的对角对应相等，两个三角形不一定全等；故不符合题意；B.添加DE=BE 后，根据已知两边和其中一边的对角对应相等，两个三角形不一定全等；故不符合题意；C.添加∠D=∠B ，根据AAS 可证明△ADE ≌△CBE ，故此选项符合题意；D.添加∠A=∠C ，根据AAS 可证明△ADE ≌△CBE ，故此选项不符合题意；故选：C【点睛】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS 、SAS 、AAS 、ASA ．关键在于应根据所给的条件判断应证明哪两个三角形全等．9．如图，要判定△ABD ≌△ACD ，已知AB ＝AC ，若再增加下列条件中的一个，仍不能说明全等，则这个条件是（ ）A ．CD ⊥AD ，BD ⊥ADB ．CD ＝BDC ．∠1＝∠2D ．∠CAD ＝∠B AD C解析：C【分析】 在△ACD 和△ABD 中，AD=AD ，AB=AC ，由全等三角形判定定理对选项一一分析，排除不符合题意的选项即可．【详解】解：添加A 选项中条件可用HL 判定两个三角形全等，故选项A 不符合题意；添加B 选项中的条件可用SSS 判定两个三角形全等，故选项B 不符合题意；添加C 选项中的条件∠1＝∠2可得∠CDA=∠BDA ，结合已知条件不SS 判定两个三角形全等，故选项C 符合题意；添加D 选项中的条件可用SAS 判定两个三角形全等，故选项D 不符合题意．故选：C ．【点睛】本题考查了全等三角形的判定，判定三角形全等的方法：SSS 、SAS 、ASA 、AAS ，判断直角三角形全等的方法：“HL”．10．已知，如图，OC 是∠AOB 内部的一条射线，P 是射线OC 上任意点，PD ⊥OA ，PE ⊥OB ，下列条件中：①∠AOC ＝∠BOC ，②PD ＝PE ，③OD ＝OE ，④∠DPO ＝∠EPO ，能判定OC 是∠AOB 的角平分线的有（ ）A ．1个B ．2个C ．3个D ．4个D解析：D【分析】 根据角平分线的性质、全等三角形的判定定理和性质定理判断即可．【详解】解：∵∠AOC ＝∠BOC ，∴OC 是∠AOB 的角平分线，① 符合题意；∵PD ⊥OA ，PE ⊥OB ，PD ＝PE ，∴OC 是∠AOB 的角平分线，② 符合题意；在Rt △POD 和Rt △POE 中，OD DE OP OP=⎧⎨=⎩ ， ∴Rt △POD ≌Rt △POE ，∴∠AOC ＝∠BOC ，∴OC 是∠AOB 的角平分线，③ 符合题意；∵∠DPO=∠EPO ，PD ⊥OA ，PE ⊥OB∴在△POD 和△POE 中，DPO EPO PDO PEO OP OP =⎧⎪=⎨⎪=⎩∠∠∠∠∴△POD ≌△POE （AAS ），∴∠AOC ＝∠BOC ，∴OC 是∠AOB 的角平分线，④ 符合题意，故选：D ．【点睛】本题考查的是角平分线的性质、全等三角形的判定与性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键；二、填空题11．如图，AC=BC ，请你添加一个条件，使AE=BD ．你添加的条件是：________．∠A=∠B 或CD=CEAD=BE ∠AEC=∠BDC 等【分析】根据全等三角形的判定解答即可【详解】解：因为AC=BC ∠C=∠C 所以添加∠A=∠B 或CD=CEAD=BE ∠AEC=∠BDC 可得△ADC 与△解析：∠A=∠B 或CD=CE 、AD=BE 、∠AEC=∠BDC 等【分析】根据全等三角形的判定解答即可．【详解】解：因为AC=BC ，∠C=∠C ，所以添加∠A=∠B 或CD=CE 、AD=BE 、∠AEC=∠BDC ，可得△ADC 与△BEC 全等，利用全等三角形的性质得出AD=BE ，故答案为：∠A=∠B 或CD=CE 、AD=BE 、∠AEC=∠BDC ．【点睛】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS 、SAS 、ASA 、AAS 、HL ．注意：AAA 、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．12．如图所示的是一张直角ABC 纸片（90C ∠=︒），其中30BAC ∠=︒，如果用两张完全相同的这种纸片恰好能拼成如图2所示的ABD △，若2BC =，则ABD △的周长为______．12【分析】根据题意证明三角形全等即可得解；【详解】如图所示由题可知∴∴∴BCD 在一条直线上∵∴△ABD 是等边三角形∴△ABD 的周长；故答案是12【点睛】本题主要考查了全等三角形的判定与性质结合等边解析：12【分析】根据题意证明三角形全等即可得解；【详解】如图所示，由题可知ABC ADC ≅△△，∴30BAC DAC ∠=∠=︒，90ACB ACD ∠=∠=︒，2BC BD ==，∴60BAD ∠=︒，180BCD ∠=︒，∴B ，C ，D 在一条直线上，∵60B D ∠=∠=︒，∴△ABD 是等边三角形，∴△ABD 的周长()3312BD BC CD ==+=； 故答案是12．【点睛】本题主要考查了全等三角形的判定与性质，结合等边三角形的性质计算是解题的关键． 13．已知在△ABC 中，AB ＝9，中线AD ＝4，那么AC 的取值范围是____1＜AC ＜17【分析】作出图形延长AD 至E 使DE ＝AD 然后利用边角边证明△ABD 和△ECD 全等根据全等三角形对应边相等可得AB ＝CE 再利用三角形的任意两边之和大于第三边三角形的任意两边之差小于第三边解析：1＜AC ＜17【分析】作出图形，延长AD 至E ，使DE ＝AD ，然后利用“边角边”证明△ABD 和△ECD 全等，根据全等三角形对应边相等可得AB ＝CE ，再利用三角形的任意两边之和大于第三边，三角形的任意两边之差小于第三边求出AC 的取值范围．【详解】如图，延长AD 至E ，使DE ＝AD ，∵AD 是△ABC 的中线，∴BD ＝CD ，在△ABD 和△ECD 中，BD CD ADB EDC AD DE =⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△ECD (SAS )，∴AB ＝CE ，∵AD ＝4，∴AE ＝4+4＝8，∵AC +CE ＞AC ＞CE -AE ，∴9-8＜AC ＜8+9，∴1＜AC ＜17，故答案为：1＜AC ＜17．【点睛】本题考查了全等三角形的判定与性质，三角形的任意两边之和大于第三边，三角形的任意两边之差小于第三边，“遇中线，加倍延”构造出全等三角形是解题的关键．14．如图，AB ，CD 交于点O ，AD ∥BC ．请你添加一个条件_____，使得△AOD ≌△BOC ．OA ＝OB （答案不唯一）【分析】由AD ∥BC 可得∠A ＝∠B ∠C ＝∠D 然后根据全等三角形的判定方法添加条件即可【详解】解：添加的条件是OA ＝OB 理由如下：∵AD ∥BC ∴∠A ＝∠B ∠C ＝∠D 在△AOD 和 解析：OA ＝OB （答案不唯一）【分析】由AD ∥BC 可得∠A ＝∠B ，∠C ＝∠D ,然后根据全等三角形的判定方法添加条件即可．【详解】解：添加的条件是OA ＝OB ，理由如下：∵AD ∥BC ，∴∠A ＝∠B ，∠C ＝∠D在△AOD 和△BOC 中A B AO BO AOD BOC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△AOD ≌△BOC （ASA ）．故答案为：OA ＝OB （答案不唯一）．【点睛】本题主要考查了全等三角形的判定定理和平行线的性质，掌握全等三角形的判定定理的内容是解答本题的关键．15．如图，ABC 的面积为215cm ，以顶点A 为圆心，适当长为半径画弧，分别交AC ，AB 于点M ，N ，再分别以点M ，N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，作射线AP ，过点C 作CD AP ⊥于点D ，连接DB ，则DAB 的面积是______2cm ．【分析】如图延长CD 交AB 于E 由题意得AP平分∠CAB 证明△ADC ≌△ADE 得到CD=DE 由此得到推出即可得到答案【详解】如图延长CD 交AB 于E 由题意得AP 平分∠CAB ∴∠CAD=∠EAD ∵CD ⊥A 解析：152【分析】如图，延长CD 交AB 于E ，由题意得AP 平分∠CAB ，证明△ADC ≌△ADE ，得到CD=DE ，由此得到,ACD ADE BCD BED SS S S ==，推出ACD BCD ADE BED S S S S +=+，即可得到答案．【详解】如图，延长CD 交AB 于E ，由题意得AP 平分∠CAB ，∴∠CAD=∠EAD,∵CD ⊥AD ，∴∠ADC=∠ADE ，∵AD=AD ，∴△ADC ≌△ADE ，∴,ACD ADE BCD BED SS S S ==， ∴ACD BCD ADE BED SS S S +=+， ∴12ABD ADE BED ABC S S S S =+==152， 故答案为：152． ．【点睛】此题考查三角形角平分线的作图方法，全等三角形的判定及性质，证出CD=DE 得到,ACD ADE BCD BED S S S S ==是解此题的关键．16．如图，ABC 中，∠C ＝90°，AD 平分∠BAC ， AB ＝5，CD ＝2，则ABD △的面积是______5【分析】根据角平分线的性质求出DE 根据三角形的面积公式计算即可；【详解】如图：作DE ⊥AB 于点E ∵AD 平分∠BAC ∠C=90°DE ⊥AB ∴DE=DC=2∵AB=5∴△ABD 的面积=×AB×DE=5解析：5【分析】根据角平分线的性质求出DE ，根据三角形的面积公式计算即可；【详解】如图：作DE ⊥AB 于点E ，∵AD 平分∠BAC ，∠C=90°，DE ⊥AB ，∵AB=5∴△ABD 的面积=12×AB×DE=5， 故答案为：5．【点睛】本题考查了角平分线的性质，掌握角平分线上的点到角的两边的距离相等是解题的关键； 17．如图，四边形ABDC 中，对角线AD 平分BAC ∠，136ACD ∠=︒，44BCD ∠=︒，则ADB ∠的度数为_____【分析】先添加辅助线过点作交的延长线于点过点作交的延长线于点过点作于点根据角平分线的判定性质定义以及三角形外角的性质邻补角的定义角的和差等可求得【详解】解：过点作交的延长线于点过点作交的延长线于点过解析：46︒【分析】先添加辅助线“过点D 作DE AB ⊥交AB 的延长线于点E ，过点D 作DF AC ⊥交AC 的延长线于点F ，过点D 作DG BC ⊥于点G ”，根据角平分线的判定、性质、定义以及三角形外角的性质、邻补角的定义、角的和差等可求得()1462ADB CBE BAC ∠=∠-∠=︒．【详解】解：过点D 作DE AB ⊥交AB 的延长线于点E ，过点D 作DF AC ⊥交AC 的延长线于点F ，过点D 作DG BC ⊥于点G ，如图：∵AD 平分BAC ∠，DE AB ⊥，DF AC ⊥ ∴12BAD BAC ∠=∠，DE DF = ∵136ACD ∠=︒ ∴18044DCF ACD ∠=︒-∠=︒∵44BCD ∠=︒，92ACB ACD BCD ∠=∠-∠=︒∴CD 平分BCF ∠∵DF AC ⊥，DG BC ⊥∴DF DG =∴DE DG =∵DE AB ⊥，DG BC ⊥∴BD 平分CBE ∠ ∴12DBE CBE ∠=∠ ∴ADB DBE BAD ∠=∠-∠1122CBE BAC =∠-∠ ()12CBE BAC =∠-∠ 12BCA =∠ 46=︒．故答案是：46︒【点睛】本题考查了角平分线的判定、性质、定义以及三角形外角的性质、邻补角的定义、角的和差等，熟练掌握相关知识点是解题的关键．18．如图，在四边形ABCD 中，90A ∠=︒，3AD =，连接BD ，BD CD ⊥，BD 平分ABC ∠．若P 是BC 边上一动点，则DP 长的最小值为______．3【分析】过D 作DE ⊥BC 于EDE 即为DP 长的最小值由题意可以得到△BAD ≌△BED 从而得到DE 的长度【详解】解：如图过D 作DE ⊥BC 于EDE 即为DP 长的最小值由题意知在△BAD 和△BED 中∴△BA解析：3【分析】过D 作DE ⊥BC 于E ，DE 即为DP 长的最小值，由题意可以得到△BAD ≌△BED ，从而得到DE 的长度．【详解】解：如图，过D 作DE ⊥BC 于E ，DE 即为DP 长的最小值，由题意知在△BAD 和△BED 中，A DEB ABD EBD BD BD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BAD ≌△BED ，∴ED=AD=3，故答案为3．【点睛】本题考查三角形全等的应用，熟练掌握三角形全等的判定和性质是解题关键．19．如图，在Rt △ABC 中，∠C ＝90°，D 、E 分别为边BC 、AB 上的点，且AE ＝AC ，DE ⊥AB ．若∠ADC ＝61°，则∠B 的度数为_____．32°【分析】由HL 可证明△ADE ≌△ADC 得出∠ADE ＝∠ADC ＝61°再根据直角三角形两个锐角互余即可得出结论【详解】解：∵DE ⊥AB ∴∠AED ＝90°＝∠DEB 在Rt △ADE 和Rt △ADC 中∴解析：32°【分析】由HL 可证明△ADE ≌△ADC ，得出∠ADE ＝∠ADC ＝61°，再根据直角三角形两个锐角互余即可得出结论．【详解】解：∵DE ⊥AB ，∴∠AED ＝90°＝∠DEB ，在Rt △ADE 和Rt △ADC 中，AD AD AE AC =⎧⎨=⎩， ∴Rt △ADE ≌Rt △ADC （HL ），∴∠ADE ＝∠ADC ＝61°，∴∠BDE ＝180°﹣61°×2＝58°，∴∠B ＝90°﹣58°＝32°．故答案为：32°．【点睛】本题考查了全等三角形的判定及性质问题，解题的关键是能够熟练掌握全等三角形的判定及性质．20．如图，已知点(44)A -，，一个以A 为顶点的45︒角绕点A 旋转，角的两边分别交x 轴正半轴，y 轴负半轴于E 、F ，连接EF ．当△AEF 直角三角形时，点E 的坐标是________．或【分析】根据等腰三角形的性质作辅助线构造全等三角形得到对应线段相等即可得到结论【详解】①如图所示：∴∵∴∵∴∴在△和中∴△△FDE ∴∴②当时同①的方法有：∴综上所述满足条件的点坐标为或故答案为：或解析：(8)0，或(40)， 【分析】根据等腰三角形的性质，作辅助线构造全等三角形，得到对应线段相等即可得到结论．【详解】①如图所示：90AFE ︒∠=，∴90AFD OFE ︒∠+∠=，∵90OFE OEF ︒∠+∠=，∴AFD OEF ∠=∠，∵90AFE ︒∠=，45EAF ︒∠=，∴45AEF EAF ︒∠==∠，∴AF EF =，在△ADF 和FOE 中，ADE FOE AFD OEF AF EF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADF ≌△FDE ，∴4FO AD ==，8OE DF OD FO ==+=，∴(40)E ，． ②当90AEF ︒∠=时，同①的方法有：8OF =，4OE =，∴(40)E ，， 综上所述，满足条件的点E 坐标为(8)0，或(40)， 故答案为：(8)0，或(40)， 【点睛】本题考查三角形全等性质和判定、等腰直角三角形的性质，注意直角三角形按角分类讨论分三种情况，不要漏解．三、解答题21．如图所示，△ABC 中，∠ACB=90°，AC=BC ，直线EF 经过点C ，BF ⊥EF 于点F ，AE ⊥EF 于点E ．（1）求证：△ACE ≌△CBF ；（2）如果AE 长12cm ，BF 长5cm ，求EF 的长．解析：（1）证明见解析；（2）EF=17cm ．【分析】（1）根据垂直的定义可得∠AEC=∠CFB=90°，然后求出∠EAC=∠FCB ，再利用“角角边”证明即可；（2）由全等三角形的性质可得：AE=CF ，CE=BF ，再根据线段的和差求解即可．【详解】（1）证明：在Rt △ACB 中，∵∠ACB=90°，∴∠ACE+∠BCF=90°∵AE ⊥EF ，BF ⊥EF∴∠ACE+∠EAC=90°∴∠CAE=∠BCF又∵ AC=CB∴△ACE ≌△CBF(ASA)(2)由△ACE ≌△CBF 可得:AE=CF=12cm ， EC=BF=5cm ，∴EF=EC+CF=12+5=17cm ．【点睛】本题考查了全等三角形的判定与性质，同角的余角相等的性质，熟练掌握三角形全等的判断方法并找出全等的条件是解题的关键．22．（阅读理解）课外兴趣小组活动时，老师提出了如下问题：如图1，ABC 中，若8AB =，6AC =，求BC 边上的中线AD 的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD 到点E ，使DE AD =，请根据小明的方法思考：（1）由已知和作图能得到ADC ≌EDB △的理由是______．（2）求得AD 的取值范围是______．（感悟）解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．（问题解决）（3）如图2，在ABC 中，点D 是BC 的中点，点M 在AB 边上，点N 在AC 边上，若DM DN ⊥，求证：BM CN MN +>．解析：（1）SAS ；（2）17AD <<；（3）见解析【分析】（1）根据AD=DE ，∠ADC=∠BDE ，BD=DC 推出△ADC 和△EDB 全等即可；（2）根据全等得出BE=AC=6，AE=2AD ，由三角形三边关系定理得出8-6＜2AD ＜8+6，求出即可；（3）延长ND 至点E ，使DE DN =，连接BE 、ME ，证明BED ≌()SAS CND △，得到BE CN =，根据三角形三边关系解答即可．【详解】（1）解：∵在△ADC 和△EDB 中，AD DE ADC BDE BD CD =⎧⎪∠=∠⎨⎪=⎩，∴△ADC ≌△EDB （SAS ），故答案为：SAS ；（2）解：∵由（1）知：△ADC ≌△EDB ，∴BE=AC=6，AE=2AD ，∵在△ABE 中，AB=8，由三角形三边关系定理得：8-6＜2AD ＜8+6，∴1＜AD ＜7，故答案为：1＜AD ＜7．（3）证明：延长ND 至点E ，使DE DN =，连接BE 、ME ，如图所示：∵点D 是BC 的中点，∴BD CD =．在BED 和CND △中，DE DN BDE CDN BD CD =⎧⎪∠=∠⎨⎪=⎩， ∴BED ≌()SAS CND △，∴BE CN =，∵DM DN ⊥，DE DN =，∴ME MN =，在BEM △中，由三角形的三边关系得：BM BE ME +>，∴BM CN MN +>．【点睛】本题是三角形综合题，主要考查了三角形的中线，三角形的三边关系定理，全等三角形的性质和判定等知识点，主要考查学生运用定理进行推理的能力．23．如图，已知A ABC ∠=∠，D CBD ∠=∠，ABD CBD ∠=∠，点E 在BC 的延长线上．求证：CD 平分ACE ∠．解析：见解析【分析】根据题意，先证明//AB CD ，然后由平行线的性质以及等量代换，得到ACD DCE ∠=∠，即可得到结论成立．【详解】证明：D CBD ∠=∠，ABD CBD ∠=∠，D ABD ∴∠=∠，//AB CD ∴ABC DCE ∴∠=∠，A ACD ∠=∠又A ABC ∠=∠，CD ∴平分ACE ∠．【点睛】本题考查了平行线的判定和性质，角平分线的判定，解题的关键是掌握所学的知识，正确得到//AB CD ．24．如图，在ABC 和BCD △中，90BAC BCD ︒∠=∠=，AB AC =，CB CD =；延长CA 至点E ，使AE AC =；延长CB 至点F ，使BF BC =．连接AD ，AF ，DF ，EF ．延长DB 交EF 于点N ．（1）求证：AD AF =；（2）求证：BD EF =．解析：（1）证明见解析；（2）证明见解析【分析】（1）结合题意得：ABF BAC ACB ∠=∠+∠，ACD ACB BCD ∠=∠+∠，推导得ABF ACD ∠=∠；通过证明ABF ACD △≌△，即可完成证明；（2）根据（1）的结论ABF ACD △≌△得：BAF CAD ∠=∠；根据题意得90BAE ∠=；再通过证明AEF ABD △≌△，即可完成证明．【详解】（1） ∵ABF BAC ACB ∠=∠+∠，ACD ACB BCD ∠=∠+∠，90BAC BCD ︒∠=∠=∴ABF ACD ∠=∠∵BF BC =，CB CD =∴BF BC CD ==即AB AC ABF ACD BF CD =⎧⎪∠=∠⎨⎪=⎩∴ABF ACD △≌△∴AF AD =；（2）∵90BAC ︒∠=∴18090BAE BAC ∠=-∠=结合（1）的结论ABF ACD △≌△∴BAF CAD ∠=∠∵90EAF BAE BAF BAF ∠=∠-∠=-∠，90BAD BAC CAD CAD ∠=∠-∠=-∠∵AE AC =，AB AC =∴AE AC AB ==即AF AD EAF BAD AE AB =⎧⎪∠=∠⎨⎪=⎩∴AEF ABD △≌△∴BD EF =．【点睛】本题考查了三角形外角、全等三角形的知识；解题的关键是熟练掌握三角形外角、全等三角形的性质，从而完成求解．25．如图，CB 为ACE ∠的角平分线，F 是线段CB 上一点，,CA CF B E =∠=∠，延长EF 与线段AC 相交于点D ．（1）求证：AB FE =；（2）若,//ED AC AB CE ⊥，求A ∠的度数．解析：（1）证明见解析；（2）120︒．【分析】（1）先根据角平分线的定义可得ACB FCE ∠=∠，再根据三角形全等的判定定理与性质即可得证；（2）先根据平行线的性质可得B FCE ∠=∠，从而可得E FCE B ACB ∠∠=∠=∠=，再根据直角三角形的性质可得30ACB ∠=︒，然后根据三角形的内角和定理即可得．【详解】（1）CB 为ACE ∠的角平分线，ACB FCE ∴∠=∠， 在ABC 和FEC 中，B E ACB FCE CA CF ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ABC FEC AAS ∴≅，AB FE ∴=；（2）//AB CE ，F E B C ∴∠=∠，E FCE B B AC ∠=∴∠=∠∠=，ED AC ⊥，即90CDE ∠=︒，90E FCE ACB ∠∠+∠∴+=︒，即390ACB ∠=︒，解得30ACB ∠=︒，30B ∴∠=︒，180120B A ACB ∠=︒-∠=∴∠-︒．【点睛】本题考查了角平分线的定义、三角形全等的判定定理与性质、三角形的内角和定理等知识点，熟练掌握三角形全等的判定定理与性质是解题关键．26．如图，AB ⊥CB ，DC ⊥CB ， E 、F 在 BC 上，AF=DE ，BE=CF ，求证：AB =DC ．解析：见解析【分析】由BE ＝CF 得BF ＝CE ，由AB ⊥CB ，DC ⊥CB 得到∠ABF ＝∠DCE ＝90°，然后根据“HL ”可判断Rt ABF ≌Rt DCE ，则AB ＝DC 即可．【详解】证明：∵BE ＝CF ，∴BE +EF ＝CF +EF ，即BF ＝CE ，∵AB ⊥CB ，DC ⊥CB ，∴∠ABF ＝∠DCE ＝90°，∵在Rt ABF 和Rt DCE 中，AF DE BF CE =⎧⎨=⎩， ∴Rt ABF ≌Rt DCE （HL ），∴AB ＝DC ．【点睛】本题考查了直角三角形的判定与性质：有一组直角边和斜边对应相等的两直角三角形全等；全等三角形的对应角相等，对应边相等．27．如图，B 、C 、E 三点在同一条直线上，AC ∥DE ，AC ＝CE ，∠ACD ＝∠B ． 求证：△ABC ≌△CDE ．解析：见解析．【分析】首先根据AC ∥DE ，利用平行线的性质可得：∠ACB=∠E ，∠ACD=∠D ，再根据∠ACD=∠B 证出∠D=∠B ，再由∠ACB=∠E ，AC=CE 可根据三角形全等的判定定理AAS 证出△ABC ≌△CDE ．【详解】证明：∵AC ∥DE ，∴ACD D ∠=∠，BCA E ∠=∠．又∵ACD B ∠=∠，∴B D ∠=∠，又∵AC CE =，∴()ABC CDE AAS ≌．【点睛】此题主要考查了全等三角形的判定，关键是熟练掌握判定两个三角形全等的方法：SSS 、SAS 、ASA 、AAS ，选用哪一种方法，取决于题目中的已知条件．28．如图，在△ABC 中，90ACB ∠=︒，AC ＝BC ，BE ⊥CE 于E ，AD ⊥CE 于D ． （1）求证：AD ＝CE（2）AD ＝6cm ，DE ＝4cm ，求BE 的长度解析：（1）证明见解析；（2）2cm ．【分析】（1）先根据垂直的定义可得90ADC E ∠=∠=︒，再根据直角三角形的两锐角互余、等量代换可得CAD BCE ∠=∠，然后根据三角形全等的判定定理与性质即可得证；（2）先结合（1）的结论可得6CE cm =，再根据线段的和差可得2CD cm =，然后根据全等三角形的性质即可得．【详解】（1）,AD CE BE CE ⊥⊥，90ADC E ∠=∠=∴︒，90CAD ACD ∴∠+∠=︒，90ACB ∠=︒，90BCE ACD ∴∠+∠=︒，CAD BCE ∴∠=∠，在ACD △和CBE △中，ADC E CAD BCE AC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ACD CBE AAS ∴≅，AD CE ∴=；（2）由（1）已证：AD CE =，6AD cm =，6CE cm ∴=，4DE cm =，2CD CE DE cm ∴=-=，又由（1）已证：ACD CBE ≅，2BE CD cm ∴==．【点睛】本题考查了直角三角形的两锐角互余、三角形全等的判定定理与性质等知识点，熟练掌握三角形全等的判定定理与性质是解题关键．。
全等三角形提高题目及答案
1. 如图所示，△ ABW A ADE ,BC 的延长线过点 /B=50°，求/ DEF 的度数。
E , / ACB= / AED=10 5 ,/ CAD=1 02.3. 如图所示，在△ ABC 中，/ A=90°, EDC 则/ C 的度数是多少？5.已知，如图所示, 是多少？4.7.如图，AD 是厶ABC 的角平分线，DEI AB, DF 丄AC,垂足分别是 于G, AD 与EF 垂直吗？证明你的结论。
E 、F ,连接 EF,交 AD A全等三角形提高练习及答案如图所示，把△ ABC 绕点C 顺时针旋转35°,得到△ A B' C , A B'交AC 于点D, 若/ A DC=90°，则/ A= ____________6. 如图，Rt △ ABC 中，/ BAC=90 , AB=AC 分别过点 B 、C 作过点A 的垂线BC CE 垂足分别为 D E ,若 BD=3 , CE=2，贝U DE= ________________8.如图所示，在△ ABC 中，AD 为/ BAC 的角平分线，DE 丄AB 于E , DF 丄AC 于F ,A ABC 的面积是 28cm 2,AB=20cm, AC=8cm 求 DE 的长。
如图，△ AOB 中，/ B=30° AB '与边OB 交于点C (AD E 分别是 AG BC 上的点，若△ ADB^A EDB^AAB=AC , ED9. 已知，如图：AB=AE，/ B=Z E,Z BAC2 EAD / CAF=/ DAF 求证：AF丄CD10. 女口图，AD=BD , 为什么？C F AD 丄BC 于D, BE 丄AC 于E , AD 与BE 相交于点 H,贝U BH 与AC 相等吗？11. 如图所示，已知,AD ABC 的高，E 为AC 上一点，BE 交AD 于F ，且有BF=AC , BE 丄 AC12. △ DAC △ EBC 均是等边三角形， AF 、BD 分别与CD CE 交于点 M N,求证：(1) AE=BD(2) CM=CN (3)A CMF 为等边三角形(4) MN// BC13. 已知：如图1,点C 为线段AB 上一点，△ ACM △ CBN 都是等边三角形，AN 交MC 于点E , BM 交CN (1) 求证：AN=BM(2)求证：△ CEF 为等边三角形14. 如图所示，已知△15.已知：BD 、CE 是厶ABC 的高，点F 在BD 上, BF=AC ，点G 在CE 的延长线上，CG=AB ,求证：AG 丄AF C求证 (1) (2) AD=AGAD 与AG 的位置关系如何H D E17.如图， 求证 已知 AF=AD-CFE 是正方形 ABCD 的边CD 的中点，点F 在BC 上，且/ DAE=Z FAE18.如图所示，已知△ ABC 中，AB=AC D 是CB 延长线上一点 且 DE=DB 求证：AC=BE+BCB _/ ADB=60 , E 是 AD 上一点19.如图所示，已知在厶 AEC 中，/ E=90° , AD 平分/ EAC 求证：BE=CFDBDF L AC 垂足为 F , DB=DC 20.已知如图：AB=DE 直线 AE 、BD 相交于 C ,Z B+Z D=180° CF=CDAFAF / DE,交BD 于F 求证：21 占 八如图 连接 OC 是/ AOB 的平分线，P 是OC 上一点，PD L 0A 于D, PE L OB 于 E , F 是0C 上一 DF和 EF ,求证：DF=EF A22. 占 八、、已知 D 在/A 的平分线上 如图，BF 丄AC 于点F ,CEL AB 于点E ,且BD=CD 求证 △ BDE^A CDF ( 2)JEDL16.如图：在厶ABC 中，BE 、CF 分别是 AC AB 两边上的高，在 BE 上截取BD=AC 在CF 的 延长线上截取CG=AB 连结AD AG A23. 如图，已知 AB// CD O 是/ ACD 与/ BAC 的平分线的交点， OE L AC 于 E ,且OE=2贝U AB与CD 之间的距离是多少？AEBF(3)无论DC 的两端点在 AM BN 如何移动，只要 谁成立？并说明理由。
全等三角形证明之能力提高(经典题目)
全等三角形提高题角度转化问题1．已知:如图，AB⊥AE，AD⊥AC，∠E＝∠B,DE＝CB．求证：AD＝AC．2．已知:如图，AD＝AE，AB＝AC，∠DAE＝∠BAC．求证：BD＝CE．3．已知：如图，在△MPN中，H是高MQ和NR的交点，且MQ＝NQ．求证:HN＝PM.4。
如图，在△ABC中，∠ACB＝90°，AC＝BC，直线l经过顶点C，过A、B两点分别作l的垂线AE、BF，E、F为垂足．当直线l不与底边AB相交时，求证：EF＝AE＋BF．5．已知：如图，AE⊥AB，BC⊥AB，AE＝AB,ED＝AC．求证：ED⊥AC．二次全等问题1.已知：如图，线段AC、BD交于O，∠AOB为钝角，AB＝CD，BF⊥AC于F，DE⊥AC于E，AE＝CF．求证：BO＝DO．2．已知:如图，AC与BD交于O点，AB∥DC，AB＝DC．若过O点作直线l，分别交AB、DC于E、F两点,求证:OE＝OF。
3．如图,E在AB上，∠1＝∠2，∠3＝∠4，那么AC等于AD吗？为什么？4．已知:如图,DE⊥AC，BF⊥AC，AD＝BC，DE＝BF.求证:AB∥DC。
5、已知：如图，AD平分∠BAC,DE⊥AB于E，DF⊥AC于F,DB=DC，求证:EB=FC【练习】1、已知∠B=∠E=90°，CE=CB，AB∥CD。
求证：△ADC是等腰三角形。
2、如图:AB=AC,ME⊥AB，MF⊥AC，垂足分别为E、F，ME=MF。
求证:MB=MCM FEC BA3、已知，△ABC 和△ECD 都是等边三角形，且点B ，C ，D 在一条直线上求证:BE=AD4、如图:在△ABC 中,∠C =90°，AD 平分∠ BAC ，DE ⊥AB 交AB 于E ，BC=30， BD ：CD=3：2,则DE= 。
5、如图，已知，EG ∥AF ，请你从下面三个条件中，再选出两个作为已知条件，另一个作为结论，推出一个正确的命题.(只写出一种情况）①AB=AC ②DE=DF ③BE=CF 已知：EG ∥AF ，________,__________ 求证：_________6、如图，在Rt △ABC 中,∠ACB=45°，∠BAC=90°,AB=AC ，点D 是AB 的中点，AF ⊥CD 于H 交BC 于F ，BE ∥AC 交AF 的延长线于E ， 求证：BC 垂直且平分DE.【思维拓展】EDCA BEDCBAG FEDC BA证明线段的和、差、倍、分问题时，常采用“割长”、“补短"等方法，构造全等三角形。
全等三角形证明50题(含答案)
全等三角形证明经典50题(含答案)1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=2ADBC2. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB延长CD 与P ，使D 为CP 中点。
连接AP ,BP ∵DP=DC,DA=DB ∴ACBP 为平行四边形 又∠ACB=90∴平行四边形ACBP 为矩形 ∴AB=CP=1/2AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边) ∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点G CG ∥EF ，可得，∠EFD ＝CGD DE ＝DC∠FDE ＝∠GDC （对顶角）BA CDF2 1 EEF＝CG∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC5.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠CA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF ∵CE ⊥AB∴∠CEB ＝∠CEF ＝90° ∵EB ＝EF ，CE ＝CE ， ∴△CEB ≌△CEF ∴∠B ＝∠CFE∵∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° ∴∠D ＝∠CFA ∵AC 平分∠BAD ∴∠DAC ＝∠FAC ∵AC ＝AC∴△ADC ≌△AFC （SAS ） ∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DEADB C∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=28. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB解：延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE＜AE＜AB+BE∵AB=4即4-2＜2AD＜4+21＜AD＜3∴AD=29.已知：BC=DE，∠B=∠E，∠C=∠D，F是CD中点，求证：∠1=∠2证明：连接BF和EF。
全等三角形证明经典40题(含答案)
1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD 的长.解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=22. 已知：BC=ED ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
AD B C3. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG∥EF 交AD 的延长线于点GCG∥EF，可得，∠EFD＝CGDDE ＝DC∠FDE＝∠GDC（对顶角）∴△EFD≌△CGDEF ＝CG∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC 为等腰三角形，AC ＝CG又 EF ＝CG∴EF ＝AC4. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠ C证明：延长AB 取点E ，使AE ＝AC ，连接DE∵AD 平分∠BAC∴∠EAD ＝∠CAD∵AE ＝AC ，AD ＝AD∴△AED ≌△ACD （SAS ）∴∠E ＝∠C∵AC ＝AB+BD∴AE ＝AB+BD∵AE ＝AB+BE∴BD ＝BE∴∠BDE ＝∠EBACDF21 E A∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C5.已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE上取F，使EF＝EB，连接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF，CE＝CE，∴△CEB≌△CEF(SAS)∴∠B＝∠CFE∵∠B＋∠D＝180°，∠CFE＋∠CFA＝180°∴∠D＝∠CFA∵AC平分∠BAD∴∠DAC＝∠FAC∵AC＝AC∴△ADC≌△AFC（SAS）∴AD＝AF∴AE＝AF＋FE＝AD＋BE6. 如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。
全等三角形经典题型50题(含答案)
全等三角形证明经典50题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB —BE 〈AE<AB+BE 即：10-2<2AD<10+2 4〈AD 〈6 又AD 是整数，则AD=52. 已知：D 是AB 中点,∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点,求证:∠1=∠2证明：连接BF 和EF 。
因为 BC=ED ，CF=DF ，∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边）.所以 BF=EF,∠CBF=∠DEF 。
连接BE.在三角形BEF 中，BF=EF.所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED.所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中，AB=AE ，BF=EF ，∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2）。
ADBC4. 已知:∠1=∠2，CD=DE ，EF//AB ，求证:EF=AC 证明：过E 点，作EG//AC,交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE （AAS ）∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC,AC=AB+BD ，求证:∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB,AD=AD ∴⊿AED ≌⊿A BD （SAS ）∴∠AED=∠B ，DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠ED C ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证:AE=AD+BE证明： 在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥AB 所以∠CEB＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ， 所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°,∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC 所以△ADC ≌△AFC(SAS ） 所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE12。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
全等三角形提高练习
1.如图所示，△ABC9Z\ADE, BC 的延长线过点E, ZACB=ZAED=105° , ZCAD二10° , ZB二50°,求ZDEF 的度数o 2•如图，AA0B中，ZB二30°,将AAOB绕点0顺时针旋转52°得到ZkA' OB'边A' B r与边0B交于点C （A‘不在OB上），则CO的度数为________________________ o
3.如图所示，在厶血。
中，ZA=90° , D,E分别是AC, BC上的点，若厶ADB^ AEDB^ AEDC,则ZC的度数是o 4•如图所示,把ZkABC绕点C顺时针旋转35°,得到M B x C,A r B x交AC于点D,若ZA‘ DC二90。
, 则ZA 二o
5.已知，如图所示，AB=AC, AD丄BC 于D,且AB+AC+BC二50c叫而AB+BD+AD=40cin,则AD二 ___
C
D
B
R
6.如图，RtAABC中,ZBAC=90° , AB二AC,分别过点B, C,作过点A的直线的垂线BD, CE,垂足为D, E, 若BD二3, CE=2,则DE二 ___________________ .
7.如图，AD是AABC的角平分线，DE丄AB,DF丄AC,垂足分别是E,F,连接EF,交AD于G, AD与EF垂直吗？证明你的结论。
8 •如图所示，在AABC中，AD为ZBAC的角平分线，DE丄AB于E, DF丄AC于F, A ABC的面积是28cm:,
AB=20c叫AC=8cm,求DE 的长。
9•已知，如图，AB二AE, ZB二ZE, ZBAC二ZEAD, ZCAF=ZDAF.求证：AF±CD
10•如图，AD二BD,AD丄BC于D, BE丄AC于E, AD于BE相交于点H,则BH与AC相等吗？为什么？
11 •如图所示，已知，AD为AABC的高，E为AC上一点，BE交AD于F，且有BF二AC, FD二CD. 求证：BE
丄AC
12. ZiDAC, ZiEBC均是等边三角形，AE, BD分别与CD, CE交于点斗N, 求证：(1) AE二BD (2)CM=CN (3) Z\CMN
为等边三角形(4) MN〃BC
13.已知：如图1,点C为线段AB上一点，A ACM, Z\CBN都是等边三角形，AN交HC于点E, BM交CN 于点F.
⑴求证：AN二BM：
(2)求证：ACEF为等边三角形；
(3)将△ACH绕点C按逆时针方向旋转90°,其他条件不变，在图2中补出符合要求的图形，并判断第
(1)、(2)两小题的结论是否仍然成立(不要求证明).
14•如图所示，已知AABC和ABDE都是等边三角形。
下列结论：①AE二CD；②BF二BG；③BH平分ZAHD；
④ZAHC=60°,⑤Z\BFG是等边三角形；⑥FG〃AD°其中正确的有( )
15•已知：BD, CE 是AABC 的高，点F 在BD 上，BF=AC,点G 在CE 的延长线上，CG 二AB. 求证:AG 丄AF
如图所示，已知AABC 中，AB 二AC,D 是CB 延长线上一点，ZADB 二60° , E 是AD 上一点，且DE 二DB,求 证：AC 二BE+BC
16
•如图：在AABC 中，BE 、CF 分别是AC 、AB 两边上的高，在BE 上截取BD 二AC,在CF 的延长线上截取
CG 二AB,连结 AD 、AGo
求证：（1） AD 二AG,
（2） AD 与AG 的位置关系如
17•如图，已知E 是正方形ABCD 的边CD 的中点，点F 在BC 上，且ZDAE=ZFAE. 求
证：AF 二AD+CF B C
A
19•如图所示，已知在ZiAEC中，ZE二90° , AD平分ZEAC, DF丄AC,垂足为F, DB二DC. 求证：BE二CF・
20•已知：如图3-50, AB=DE,直线AE, BD 相交于C, ZB+ZD=180° , AF〃DE,交BD 于F・求证：CF=CD.
21 •如图，0C是ZA0B的平分线, P是0C上一点，PD丄0A于D,
PE丄0B于E, F是0C上一点,连接DF和EF,求证:DF=EFo
22•已知：如图，BF丄AC于点F, CE丄AB于点E,且BD二
CD
求证：(l)ABDE^ACDF (2)点D在ZA的平分线上
23如图，已矢0 AB/7CD, O是ZACD与ZBAC的平分线的交点，OE丄AC于E,且OE=2,贝lj AB 与CD之间的距离为____________________
24•如图，过线段AB的两个端点作射线AM、BN,使AM/7BN,按下列要求画图并回答：
画ZMAB、ZNBA的平分线交于E。
（1） ZAEB是什么角？
（2）过点E作一直线交AM于D,交BN于C,观察线段DE、CE,你有何发现？
（3）无论DC的两端点在AM、B\如何移动，只要DC经过点E,①AD+BC二AB；②AD+BC二CD谁成立？并说明理由。
26 •如图，△ABC的三边43、BC、C4长分别是20、30、40,其三条角平
分线将△ ABC分为三个三角形，则耳加。
：S'BCO : S ACO等于（
A. 1 ： 1 ： 1 B・ 1 ： 2 ： 3 C・ 2 ： 3 ： 4 D・ 3 ： 4 ： 5
27・正方形ABCD 中，AC. BD 交于0, ZE0F=90°,已知AE = 3,CF=4, 贝lj S ABEF
为_____________ ■
29・如图，在R/AABC 中，ZACB=45°, ZBAC=90°, AB二AC,点D 是AB 的中点，AF丄
CD 于H 交
BC于F, BE〃AC交AF的延长线于E,求证：BC垂直且平分DE.
D
30.在ZiABC 中，ZACB = 90°, AC=BC,直线MN 经过点C,且AD丄MN 于D, BE丄MN 于E.
⑴当直线MN绕点C旋转到图⑴的位置时，求证：DE=AD+BE
⑵当直线MN绕点C旋转到图⑵的位置时，求证：DE=AD—BE;
⑶当直线MN绕点C旋转到图⑶的位置时，试问DE、AD、BE具有怎样的等量关系？请直接写出这个等量关系.
N B。