空间向量之建立空间直角坐标系的方法及技巧
空间向量之 建立空间直角坐标系的方法及技巧

空间向量之 建立空间直角坐标系的方法及技巧 .一、利用共顶点的互相垂直的三条棱构建直角坐标系例1 已知直四棱柱ABCD -A 1B 1C 1D 1中,AA 1=2,底面ABCD 是直角梯形,∠A 为直角,AB ∥CD ,AB =4,AD =2,DC =1,求异面直线BC 1与DC 所成角的余弦值.解析:如图1,以D 为坐标原点,分别以DA 、DC 、DD 1所在直线为x 、y 、z 轴建立空间直角坐标系,则C 1(0,1,2)、B (2,4,0),∴1(232)BC =--,,,(010)CD =-,,. 设1BC 与CD 所成的角为θ,则11317cos 17BC CDBC CD θ==. 二、利用线面垂直关系构建直角坐标系例2 如图2,在三棱柱ABC -A 1B 1C 1中,AB ⊥侧面BB 1C 1C ,E 为棱CC1上异于C 、C 1的一点,EA ⊥EB 1.已知AB =BB 1=2,BC =1,∠BCC 1=3π.求二面角A -EB 1-A 1的平面角的正切值. 解析:如图2,以B 为原点,分别以BB 1、BA 所在直线为y 轴、z 轴,过B 点垂直于平面AB 1的直线为x 轴建立空间直角坐标系.由于BC =1,BB 1=2,AB BCC 1=3π, ∴在三棱柱ABC -A 1B 1C1中,有B (0,0,0)、A (0,、B 1(0,2,0)、1022c ⎛⎫- ⎪ ⎪⎝⎭,、1302C ⎫⎪⎪⎝⎭,,. 设0E a ⎫⎪⎪⎝⎭,且1322a -<<,由EA ⊥EB 1,得10EA EB =,即320a a ⎛⎛⎫--- ⎪ ⎪⎝⎝⎭,, 233(2)2044a a a a =+-=-+=,∴13022a a ⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭, 即12a =或32a =(舍去).故102E ⎫⎪⎪⎝⎭,,. 由已知有1EA EB ⊥,111B A EB⊥,故二面角A -EB 1-A 1的平面角θ的大小为向量11B A 与EA的夹角.因11(00B A BA ==,12EA ⎛=- ⎝ 故11112cos 3EA B A EA B A θ==,即tan 2θ= 三、利用面面垂直关系构建直角坐标系例3 如图3,在四棱锥V -ABCD 中,底面ABCD 是正方形,侧面VAD 是正三角形,平面VAD ⊥底面ABCD .(1)证明AB ⊥平面VAD ;(2)求面VAD 与面VDB 所成的二面角的余弦值.解析:(1)取AD 的中点O 为原点,建立如图3所示的空间直角坐标系.设AD =2,则A (1,0,0)、D (-1,0,0)、B (1,2,0)、V ,∴AB =(0,2,0),VA =(1).由(020)(103)0AB VA =-=,,,,,得 AB ⊥VA .又AB ⊥AD ,从而AB 与平面VAD 内两条相交直线VA 、AD 都垂直,∴ AB ⊥平面VAD ;(2)设E 为DV的中点,则102E ⎛- ⎝⎭∴302EA ⎛= ⎝⎭,,,322EB ⎛= ⎝⎭,,,(10DV =.∴332(103)02EB DV ⎛⎫=-= ⎪ ⎪⎝⎭,,,,, ∴EB ⊥DV .又EA ⊥DV ,因此∠AEB 是所求二面角的平面角.∴21cos 7EA EBEA EB EA EB ==,.故所求二面角的余弦值为7. 四、利用正棱锥的中心与高所在直线构建直角坐标系例4 已知正四棱锥V -ABCD 中,E 为VC 中点,正四棱锥底面边长为2a ,高为h .(1)求∠DEB 的余弦值;(2)若BE ⊥VC ,求∠DEB 的余弦值.解析:(1)如图4,以V 在平面AC 的射影O 为坐标原点建立空间直角坐标系,其中O x ∥BC ,O y ∥AB ,则由AB =2a ,OV =h ,有B (a ,a ,0)、C (-a ,a ,0)、D (-a ,-a ,0)、V (0,0,h )、222a a h E ⎛⎫- ⎪⎝⎭,, ∴3222a h BE a ⎛⎫=-- ⎪⎝⎭,,,3222a h DE a ⎛⎫= ⎪⎝⎭,,. ∴22226cos 10BE DEa h BE DE a h BE DE -+==+,, 即22226cos 10a h DEB a h -+=+∠; (2)因为E 是VC 的中点,又BE ⊥VC ,所以0BE VC =,即3()0222a h a a a h ⎛⎫----= ⎪⎝⎭,,,,,∴22230222a h a --=,∴h =. 这时222261cos 103a h BE DE a h -+==-+,,即1cos 3DEB =-∠.五、利用图形中的对称关系建立坐标系图形中虽没有明显交于一点的三条直线,但有一定对称关系(如正三棱柱、正四棱柱等),利用自身对称性可建立空间直角坐标系.例5已知两个正四棱锥P -ABCD 与 Q -ABCD 的高都为2,AB =4.(1)证明:PQ ⊥平面ABCD ;(2)求异面直线AQ 与PB 所成的角;(3)求点P 到平面QAD 的距离.(2)由题设知,ABCD 是正方形,且AC ⊥BD .由(1),PQ ⊥平面ABCD ,故可分别以直线CA DB QP,,为x ,y ,z 轴建立空间直角坐标系(如图1),易得(2202)(022)AQ PB =--=-,,,,,1cos 3AQ PBAQ PB AQ PB <>==,.所求异面直线所成的角是1arccos 3. (3)由(2)知,点(0(22220)(004)D AD PQ -=--=-,,,,,,. 设n =(x ,y ,z )是平面QAD 的一个法向量,则00AQ AD ⎧=⎪⎨=⎪⎩,,n n 得00z x y +=+=⎪⎩,,取x =1,得(11-,,n =.点P 到平面QAD 的距离22PQ d ==nn .点评:利用图形所具备的对称性,建立空间直角坐标系后,相关点与向量的坐标应容易得出.第(3)问也可用“等体积法”求距离.。
建立空间直角坐标系的方法及技巧

建立空间直角坐标系的方法及技巧1.确定坐标轴方向:首先需要确定空间直角坐标系的坐标轴方向,通常选择三个相互垂直的轴,分别称为x轴、y轴和z轴。
可以选择其中一个轴为参考轴,然后使用右手定则来确定其他两个轴的方向。
在右手定则中,将右手的拇指、食指和中指分别与x、y和z轴对齐,那么食指和中指所形成的平面就是坐标系的平面,拇指的方向就是z轴的方向。
2.确定原点位置:确定好坐标轴方向后,需要确定坐标系的原点位置。
原点通常可以选择在三维空间中的一些特殊点上,例如物体的质心、交点或者其他方便计算的点。
原点的选择应根据具体问题和需求进行确定。
3.确定单位长度:建立坐标系后,需要确定单位长度,也就是每个坐标轴上的单位距离。
单位长度的选择应根据具体问题和需求进行确定,可以根据物体的大小和所需精度进行估计。
常用的单位长度包括米、厘米、毫米等。
4.标示坐标轴刻度:在建立坐标系后,需要在每个坐标轴上标示刻度,以便表示点的位置。
可以根据需求和所测量的物体大小来确定每个刻度的长度和数量。
通常可以使用尺子、直尺等工具来测量和标示刻度。
在标示刻度时,可以选择以原点为起点,沿着每个坐标轴正方向逐个标示刻度,或者以坐标轴的负方向为起点标示刻度。
5.标示点的坐标:建立好坐标轴和刻度后,就可以根据需要来标示空间中的点的坐标。
对于一个三维空间中的点,可以通过它到坐标轴的距离来确定它的坐标值。
通常可以使用直角坐标系中的(x,y,z)来表示一个点的坐标,其中x、y和z分别是点在x轴、y轴和z轴上的坐标值。
1.灵活选择参考轴:参考轴的选择应根据具体问题和需求进行确定。
在确定参考轴时,可以考虑使问题的描述尽量简洁和直观,同时方便计算和分析。
2.注意坐标轴的方向:在确定坐标轴的方向时,使用右手定则可以帮助确定其他两个轴的方向。
要确保坐标轴的方向满足右手定则中拇指、食指和中指的排列次序。
3.注意单位长度的选择:单位长度的选择应根据具体问题和需求进行确定。
建立空间直角坐标系的几种方法

建立空间直角坐标系的几种方法1.给定坐标轴方向及原点位置:最直接的方法是给定三个坐标轴的方向及原点位置。
通常,我们选择三个相互垂直的轴,并确定它们的正方向。
例如,我们可以选择X轴向右,Y轴向上,Z轴垂直于XOY平面向外,然后选择原点为坐标轴的交点。
通过这种方法,我们就可以建立一个三维直角坐标系。
2.使用原点和两个已知点:在给定两个已知点和原点的情况下,我们可以建立一个空间直角坐标系。
首先,我们将其中一个已知点作为坐标轴上的一个点,然后确定一个与此轴垂直的第二个轴。
接下来,我们确定第三个轴的方向,使其与前两个轴正交,并选择原点位置。
通过这种方法,我们可以构建一个三维直角坐标系。
3.使用平面和轴的交点:另一种建立空间直角坐标系的方法是确定两个平面及其在坐标轴上的交点。
首先,我们选择平面XY作为参考平面,并将其与X轴和Y轴在原点处的交点作为坐标轴上的两个点。
然后,选择两个非共线的轴分别与平面XZ和平面YZ正交,并确定它们的正方向。
通过这种方法,我们可以建立一个三维直角坐标系。
4.使用向量运算:通过向量运算的方法可以建立空间直角坐标系。
首先,选择一个已知向量为其中一个坐标轴的向量。
然后,选择另一个与已知向量相互垂直的向量,并进行正规化。
接下来,使用向量叉积运算确定第三个轴的方向,并对其进行正规化。
最后,选择原点位置。
通过这种方法,我们可以建立一个三维直角坐标系。
这些方法都是建立空间直角坐标系的常见方法,可以根据具体情况选择合适的方法进行建立。
空间向量的直角坐标及其运算

∴ AP AB , AP AD,又 AB AD A , AP 平面 ABCD,
∴ AP 是平面 ABCD的法向量; 解:(2) AB 22 12 42 21 , AD 42 22 02 2 5 ,
∴ SABC
1 2
AB
AC
sin
A
101 。 2
7、在棱长为1的正方体 ABCD A1B1C1D1 中,E, F 分别是 DD1、DB 中点,G 在棱CD 上,
CG
1 4
CD
,
H
是
C1G
的中点;
(1)求证: EF B1C ;(2)求 EF 与C1G 所成的角的余弦;(3)求 FH 的长。
解:如图以 D 为原点建立直角坐标系 D xyz ,
(3)证明线面平行:若直线的方向向量与平面的一个法向量垂直,则这直线与该平面平行;
(4)证明面面平行:若两个不重合平面的法向量平行,则这两个平面就互相平行。 11、用向量求异面直线所成角:
找出两条异面直线各自的一个方向向量,计算这两个向量的夹角 ,则 (或 的补角)
即为两条异面直线所成的角。
设 a、b 是异面直线, d1 是直线 a 的一个方向向量, d2 是直线b 的一个方向向量,异面
一、基本概念:
1、空间直角坐标系:
(1)若空间的一个基底的三个基向量互相垂直,且长为1,这个基底叫单位正交基底,用 i, j,k
表示;
(2)在空间选定一点O 和一个单位正交基底 i, j,k ,以点O 为原点,分别以 i, j,k 的方向
为正方向建立三条数轴:x 轴、 y 轴、z 轴,它们都叫坐标轴;我们称建立了一个空间 直角坐标系 O xyz ,点O 叫原点,向量 i, j, k 都叫单位向量;通过每两个坐标轴的平
空间直角坐标系及向量坐标

a (ax )i (ay ) j (az )k ,
即
a b (ax bx ,ay by ,az bz ) ,
a b (ax bx ,ay by ,az bz ) ,
a (ax ,ay ,az ) .
由此可见,对向量进行加、减及数乘,只需对向量的各个坐标分别进行相应
的运算即可.
高等数学
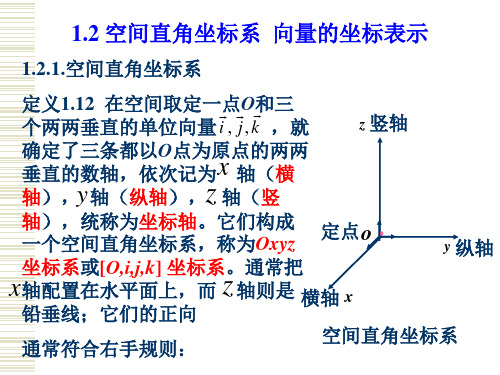
1.1 空间直角坐标系
在平面解析几何中,通过建立平面直角坐标系,把平面上的点与 二元有序实数组对应起来.同样,在空间解析几何中,通过建立空间 直角坐标系,也可以把空间的点与三元有序实数组对应起来.
如图所示,过空间一定点 O ,作三个两两垂直的单位向量 i ,j ,k ,就确定了三 条都以 O 为原点的两两垂直的数轴,依次记为 x 轴(横轴)z ) ,b (bx ,by ,bz ) , 即 a axi ay j azk ,b bxi by j bzk , 利用向量的运算律,有
a b (ax bx )i (ay by ) j (az bz )k ,
a b (ax bx )i (ay by ) j (az bz )k ,
1.2 向量的坐标表示
如图所示,设 M 为空间一点,过点 M 分别作垂直于 x 轴、 y 轴、 z 轴的平面,它 们与 x 轴、 y 轴、 z 轴分别交于 P ,Q ,R 三点,这三个点在 x 轴、 y 轴、 z 轴上的坐标分 别为 x,y,z ,这样就确定了空间点 M 的唯一一个三元有序实数组 (x ,y ,z) .反之,若 给定一个三元有序实数组 (x ,y ,z) ,分别在 x 轴、 y 轴、 z 轴找到坐标分别为 x,y,z 的 三点 P ,Q ,R ,过这三点分别作垂直于 x 轴、 y 轴、 z 轴 的平面,这三个平面有唯一交点 M ,于是就建立了空间 点 M 和三元有序实数组 (x ,y ,z) 之间的一一对应关系. 这组数 x,y,z 称为点 M 的坐标,记为 M (x ,y ,z) ,并依 次称 x,y 和 z 为点 M 的横坐标、纵坐标和竖坐标.
空间直角坐标系的建立的常见方法

一、空间一、空间直角直角坐标系的建立的常见方法坐标系的建立的常见方法运用“坐标法”解答空间运用“坐标法”解答空间几何体几何体问题时,往往需要建立空间直角坐标系.依据空间几何体的结构特征,充分利用图形中的垂直关系或构造垂直关系建立空间直角坐标系,是解决问题的基础和关键.一、利用共一、利用共顶点顶点的互相垂直的三条棱建系的互相垂直的三条棱建系 例1、在正方体ABCD -A ′B ′C ′D ′中,′中,点M 是棱AA ′的′的中点中点, 点O 是对角线BD ′的中点′的中点. .(Ⅰ)求证:OM 为异面直线AA ′和BD ′的公′的公垂线垂线; (Ⅱ)求二面角M -BC ′-B ′的大小;例2、如图,在直、如图,在直三棱柱三棱柱111ABC A B C -中,中, AB =1,13AC AA ==,∠ABC=600. (Ⅰ)证明:1AB A C ^;(Ⅱ)求二面角A —1A C —B 的大小。
二、利用线面垂直关系建系二、利用线面垂直关系建系例3、已知三棱锥P -ABC 中,PA ⊥面ABC ,AB ⊥AC , PA=AC=12AB ,N 为AB 上一点,AB=4AN, M,S 分别为PB,BC 的中点. (Ⅰ)证明:CM ⊥SN ;(Ⅱ)求SN 与平面CMN 所成角的大小. ·D ¢A BCDM OA ¢B ¢C ¢·C B A C 1B 1A 1.已知2AB =,BB 1=2,BC =1,∠BCC1ACBPz xy例4、如图,、如图,正方形正方形ABCD 和四边形ACEF 所在的所在的 平面互相平面互相垂直垂直,C E ⊥AC,EF AC,EF∥∥AC,AB=2,CE=EF=1. (Ⅰ)求证:AF ∥平面BDE ; (Ⅱ)求证:CF ⊥平面BDE ; (Ⅲ)求(Ⅲ)求二面角二面角A-BE-D 的大小。
的大小。
例5、如图,在三、如图,在三棱锥棱锥P ABC -中,2AC BC ==,90ACB Ð=,AP BP AB ==,PC AC ^.(Ⅰ)求证:PC AB ^;(Ⅱ)求二面角B AP C --的大小;的大小; (Ⅲ)求点C 到平面APB 的距离.的距离.例6、 如图2,在,在三棱柱三棱柱ABC -A 1B 1C 1中,中,AB ⊥侧面BB 1C 1C ,E 为棱CC 1上异于C 、C 1的一点,的一点, EA ⊥EB 1=3p.求二面角A -EB 1-A 1的平面角的的平面角的正切正切值.值.BC=22,SA SA==SBDBCASOyxz三、利用面面三、利用面面垂直垂直关系建系关系建系例7、如图3,在四棱锥V -ABCD 中,底面ABCD 是正方形,是正方形, 侧面VAD 是正三角形,是正三角形,平面平面VAD ⊥底面ABCD . (1)证明AB ⊥平面VAD ;(2)求面VAD 与面VDB 所成的二面角的所成的二面角的余弦余弦值.值.例8、在直、在直三棱柱三棱柱111ABC A B C -中,中, AB =BC ,D 、E 分别为11BB AC ,的中点. (1)证明:ED 为异面直线1BB 与1AC 的公的公垂线垂线; (2)设12AA AC AB ==,求二面角11A AD C --的大小.的大小.例9、四棱锥S -ABCD 中,底面ABCD 为平行四边形,侧面SBC SBC⊥底面⊥底面ABCD ABCD。
1.2空间直角坐标系-向量的坐标表示
例 8 设P 在x 轴上,它到P1(0, 2,3) 的距离为到 点 P2 (0,1,1)的距离的两倍,求点 P 的坐标.
解 因为P 在x 轴上,设P点坐标为 ( x,0,0),
PP1 x2 2 2 32 x2 11,
PP2 x2 12 12 x2 2,
B(0, y, z)
• M(x, y, z)
y
Q(0, y,0) A( x, y,0)
设空间两点A(x1, y1, z1), B(x2 , y2 , z2 ), 则点A与点B之间的距离| AB | 就是 向量AB (x2 x1, y2 y1, z2 z1)的模. 即:| AB || AB |
定点 o •
y 纵轴
横轴 x 空间直角坐标系
Ⅲ
yoz面
Ⅳ
xoy面
Ⅶ
x
Ⅷ
z zox 面
Ⅱ
o
yⅠ
Ⅵ Ⅴ
空间直角坐标系共有八个卦限
例4 在空间直角坐标系中,指出下列各
点在哪个卦限?
A(1,2,3), B(2,3,4), C(2,3,4), D(2,3,1) .
解答: A:Ⅳ; B:Ⅴ; C:Ⅷ; D:Ⅲ;
例 6 设 A( x1 , y1 , z1 )和B( x2 , y2 , z2 )为两已知 点,而在AB 直线上的点M 分有向线段AB 为
两部分AM 、MB,使它们的值的比等于某数
( 1),即 AM ,求分点的坐标.
MB
解 设 M( x, y, z)为直线上的点, z
B
AM {x x1, y y1, z z1} A M
非零向量
a
的方向角: 、
、
z
a M1M2 (ax , ay , az )
建立空间直角坐标系的几种方法

建立空间直角坐标系的几种方法方法一:直角坐标系基于物体的参考点和参考线。
首先,选择一个点作为原点,然后选择一个方向作为x轴的正方向,并将参考直线从原点开始延伸。
然后,选择与x轴垂直的方向作为y轴的正方向,并延伸直线。
最后,选择与xy平面垂直的方向作为z轴的正方向,并延伸直线。
这样,就完成了一个空间直角坐标系的建立。
方法二:直角坐标系基于坐标系的旋转和平移。
在二维平面中,我们可以通过将一个坐标系进行旋转和平移来建立另一个坐标系。
同样,在三维空间中,我们可以通过对一个已有的坐标系进行旋转和平移来建立一个新的坐标系。
通过旋转和平移的组合,我们可以得到一个新的坐标系,其中的坐标轴可以与原坐标系的坐标轴成直角。
方法三:直角坐标系基于物体的方向和参考面。
在航空航天等领域,直角坐标系通常是根据物体的方向和参考面来建立的。
例如,在航空航天器中,航天员在太空中的朝向通常是以地球为参考面建立的直角坐标系。
方法四:直角坐标系可以通过测量和计算得到。
在地理测量和地质勘探等领域,可以通过测量物体的位置和方向来确定一个直角坐标系。
测量可以通过使用全站仪或其他测量设备进行精确的三维测量来完成。
方法五:直角坐标系可以基于地图坐标系建立。
在地理信息系统(GIS)中,地图坐标系是一种基于平面坐标系的直角坐标系。
通过将地图上的点与已知的地理坐标进行对应,并利用平面坐标系的投影方法,可以建立地图坐标系。
以上是建立空间直角坐标系的几种常见方法。
这些方法在各种领域中得到广泛应用,可以帮助我们更好地理解和描述物体在空间中的位置和方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间向量之建立空间直角坐标系的方法及技巧
、禾U用共顶点的互相垂直的三条棱构建直角坐标系
例1已知直四棱柱ABC D A i B i CD中,AA= 2,底面ABCD是直角梯形,/ A为直角,AB//
CD AB= 4, AD= 2,DC= 1,求异面直线BC与DC所成角的余弦值.
解析:如图1, 以D为坐标原点,分别以DA DC DD所在直线为x、y、z轴建立空间直角
1 , 2)、B(2, 4, 0), •- BC =(-2,3,2) , CD
=(0, -1,0).
坐标系,则C (0,
设BC i与CD所成的角为v
CD 3 '17
17
二、利用线面垂直关系构建直角坐标系
例2 如图2,在三棱柱ABC- ABC中,AB丄侧面BBCQ, E为棱CC上异于C C的一点,
EAL EB.已知AB = J2 , BB = 2, BC= 1, / BCC=上.求二面角A- EB—A的平面角的正切值.
3
解析:如图2,以B为原点,分别以BB、BA所在直线为y轴、z轴,过B点垂直于平面AB 的直线为x轴建立空间直角坐标系.
由于BC= 1, BB= 2, AB= -/2,/ BCG=—,
3
•••在三棱柱ABC- ABC 中,有(0, 0, 0)、(0, 0,
C
1 第3 /
—,—,0 .
I2 2丿輛〕〔3设E — , a, 0 且一丄<a<
3
,
I2丿22
由EAL EB,得EAEB =0,
CD
BA 丄EB ,故二面角 A- EB —A i 的平面角日的大小为向量 BA 与 EA 的夹角.
訳=BA = (0,0八 2) , EA 二
三、利用面面垂直关系构建直角坐标系
例3 如图3,在四棱锥 V — ABCD 中,底面ABCD 是正方形,侧面 VAD 是正三角形,平面 VAD 丄底面ABCD
AB 丄 VA
又ABL AD 从而AB 与平面VAD 内两条相交直线 VA AD 都垂直,二 (2)设E 为DV 的中点,则
J-1显1 I 2
2丿 即「2,一皿] X ,2—aJ
< 2 丿
+a (a —2)=a 2—2a+3=0,「. 'a —丄 |
4 I 2丿
3 4 即-2或a =| (舍去).故
E 佇,,0 . ■ 3i
3 去(3,0,_Q
,时,2, -纠 辽 2丿 I 2 2丿
,DV =(1,0, 3). 由已知有EA _ EB i , 故 COS V =
灵晁^,即ta —子
EA'B 1A 1
(1)证明 AE 丄平面VAD
(2)求面 VAD 与面VDB^成的二面角的余弦值.
解析:(1) 取AD 的中点O 为原点,建立如图3所示的空间直角坐标系.
设 AD= 2,则 A (1,0,0)、D (— 1,0,0)、B ( 1,2,0)、
V (0,0,爲),二 AB =(0, 2, 0) , VA =( 1,0, — V 3 ).
由 ABVA = (0,2,0壯1,0, - . 3) = 0,得
AB 丄平面VAD
故所求二面角的余弦值为 —21
7
四、禾U 用正棱锥的中心与高所在直线构建直角坐标系
已知正四棱锥 V-ABCD 中, E 为VC 中点,正四棱锥底面边长为 2a ,高为h .
即 cos Z DEB =「6a 2 h :; 10a 1 2 +h 2
(2)因为E 是VC 的中点,又BE! VC
c 2 , 2
3 2 a h a 0 ,• h -、2a . 2 2 2
1 1
,即 cos Z DEB 二-一
• EB[DV 」i,o,J 3)=o ,
••• E 吐 DV
又 EAL DV 因此/ AEB 是所求二面角的平面角.
(1) 求/ DEB 的余弦值;
(2) 若BE! VC 求/ DEB 的余弦值.
解析: (1)如图4,以V 在平面AC 的射影
O 为坐标原点建立空间直角坐标系, 其中O x / BC O y // AB,则由 AB^ 2a , OV= h ,有 B (a ,
a , 0)、C (- a , a ,0)、D( - a , -a,0)、V (0, 0, h)、*222'丿
•晁…3a ,
I 2
a h 2 2) 丨h a,_ •- cos :. BE ,DE
BE DE 2 2 ? 10a h =o ,即 _3a,-a h I 2
2,2 心,a ,-h )“ , 这时 cos ;: BE ,DE -6a 2 h 2 10a 2 h 2
E 八EB .'21 …cos
EB _ 7
图4
所以
五、利用图形中的对称关系建立坐标系
图形中虽没有明显交于一点的三条直线,但有一定对称关系(如正三棱柱、正四棱柱等) 自身对称性可建立空间直角坐标系.
例5已知两个正四棱锥 P — ABCDf
Q-ABCD 勺高都为 2, AB= 4.
(1) 证明:PQL 平面ABCD
(2) 求异面直线 AQ 与 PB 所成的角;
(3) 求点P 到平面QAD 勺距离.
(2)由题设知,ABCDI 正方形,且ACL BD 由( 1),PQL 平面ABCD 故可分别以直线 CA, DB , QP 点评:禾U 用图形所具备的对称性,建立空间直角坐标系后,相关点与向量的坐标应容易得 出•第
(3)问也可用“等体积法”求距离. 3 3 ,利用 为x , y , z 轴建立空间直角坐标系(如图 1),易得 A5 =(—2J2Q ,- 2),PB =(0,2、2- 2), cos :: AQ ,PB =
AQ PB
1 arccos —. 3
(3)由(2)知,点 D(0,— 2矩0) AD =(—2逅,—2J2,0)PQ
所求异面直线所成的角是 = (0,0, 4).
设n = (x , y , z )是平面QAD 的一个法向量,则 0
[nLAD = 0,
得、,2x • z = 0,取 1,得 x y =0, n = (1, -1, - .2) •点P 到平面QAD 勺距离d -
PQL n
n| =2】2 .。
