排队论和库存论讲解
第10章 排队论

混合制排队系统: • 等待时间有限。即顾客在系统中 等待时间不超过某一给定的长度T, 当等待时间超过T时,顾客将自动 离开,不再回来。如易损失的电 子元件的库存问题,超过一定存 储时间的元器件被自动认为失效。
混合制排队系统: • 逗留时间(等待时间与服务时间 之和)有限。例:用高射炮射击 飞机,当敌机飞越射击有效区域 的时间为t时,若这个时间内未被 击落,也就不可能再被击落了。
第十章 排队论
10.1 引
言
排队论是研究排队系统(又称随 机服务系统)的数学理论和方法,是 运筹学的一个重要分支。 1、有形排队现象:进餐馆就餐,到 图书馆借书,车站等车,去医院看病, 售票处售票,到工具房领物品等现象。
2、无形排队现象:如几个旅客同时打电
话订车票;如果有一人正在通话,其他 人只得在各自的电话机前等待,他们分 散在不同的地方,形成一个无形的队列 在等待通电话。
均数。如果列车因站中2股道均被占 用而停在站外或前方站时,每列车 每小时费用为a元,求每天由于列车 在站外等待而造成的损失。
解:本例可看成一个M/M/1/排队问 题,其中 =2, =3,= /=2/3<1 系统中列车的平均数
L= / (1-)=(2/3)/(1-2/3)=2(列)
7、排队研究的基本问题
系统优化问题:又称为系统控制问 题或系统运营问题,其基本目的是 使系统处于最优的或最合理的状态。 包括:最优设计问题和最优运营问 题。
10.2 排队系统的数量指标及记号 1、数量指标
系统状态:也称为队长,指排队系 统中的顾客数(排队等待的顾客数 与正在接受服务的顾客数之和)。
排队的不一定是人,也可以是物。如生 产线上的原材料,半成品等待加工;因 故障而停止运行的机器设备在等待修理; 码头上的船只等待装货或卸货;要下降 的飞机因跑道不空而在空中盘旋等。
排队论模型专业知识课件

(队长)=等待服务旳顾客数+正被服务旳顾客数,所以
越大,
;排队长度则仅指在队列中
. 系统中旳顾客数
阐明服务效率越低。
(2)等待时间:是指从顾客到达时间算起到他开始接受
顾客到达时刻算起到他接受服务完毕为止所需要旳时间,
逗留时间=等待时间+服务时间 (3)忙期:是指服务台连续繁忙旳时间,即顾客从到达空闲服务台算起到服务台再次变为空闲时止旳这段时间。这是服务台最关心数量指标,它直接关系到服务员工作强度,与忙期相相应旳是闲期,这是指服务台连续保持空闲旳时间长度;显然,在排队系统中忙期与闲期,是交替出现旳。
从而在生灭过程中取
(9.5)
记 ,称为服务强度 当 时,模型不稳( 时达不到统计) 当 <1时,模型稳定,有稳定解 (3)X(t)旳分布律 由(9.12),(1.15)式得此模型旳微分差分方程组 (9.6) 当 时,稳态解满足
1.生灭过程旳定义 设有一种系统,具有有限个状态,其状态集s={0,1,2…k}或有可数个状态,状态集s={0,1,2…},令X(t)为系统在时刻t所处旳状态,若在某一时刻t系统旳状态数为n,假如对△t>0有。 (1)到达(生):在(t,t+△t)内系统出现一种新旳到达旳概率为
服务时止旳这段时间,其期望值记
;逗留时间则指从
即是顾客在系统中所花费旳总时间,其期望值记
。
排队系统除了上述三个主要数量指标外,另外服务台旳利用率(即服务员忙碌旳时间在总时间中所占百分比)在排队论旳研究中也是很主要旳指标。
(二)排队模型旳符号表达与几种主要排队模型 1.排队模型旳符号一般表达法 一般表达法 A/B/C/D/E/F A:顾客来到时间间隔旳分布类型 B:服务时间旳分布类型 C:服务员个数 D:系统容量 E:顾客源个数 F:服务规则 先来先服务旳等待排队模型主要由三参数法即A/B/C例“M/M/1/k/
排队论在物流仓储中的应用

排队论在物流仓储中的应用第一章:引言物流仓储作为现代物流体系的重要组成部分,扮演着货物集散、分拨和储存的角色。
在物流仓储过程中,如何有效地组织货物流动,提高仓储效率成为一个重要问题。
排队论作为一种数学模型,能够帮助我们预测和优化排队系统,同时也可以应用于物流仓储中。
本文将介绍排队论在物流仓储中的应用,并探讨其对物流仓储效率的影响。
第二章:排队论基础知识2.1 排队系统的基本组成排队系统一般由顾客、服务器和排队区域组成。
顾客指需要等待服务的单位,服务器指提供服务的单位,排队区域指顾客等待服务的区域。
2.2 排队模型排队模型主要包括M/M/1模型、M/M/c模型、M/G/1模型等。
其中,M表示到达率服从指数分布,G表示到达率服从一般分布,1表示单个服务器,c表示多个服务器。
不同的排队模型适用于不同的排队系统,可以通过模型来分析和优化系统性能。
第三章:排队论在物流仓储中的应用3.1 仓库收货区排队系统在物流仓储中,收货是货物进入仓库并进行初步处理的环节。
由于货物到达时间和数量的不确定性,仓库的收货区常常面临排队问题。
可以利用排队论来分析和优化收货区的服务水平和资源配置,以提高仓库的收货效率。
3.2 仓库出货区排队系统仓库的出货区是货物出仓库之前的最后一站,也是货物离开仓库的关键环节。
通过排队论模型,可以预测出货区的等待时间和排队长度,从而合理安排出货计划和资源配置,减少货物等待时间,提高出货效率。
3.3 仓库货架排队系统仓库货架是存放货物的重要设施,高效的货架排队系统可以使货物存储和取出的过程更加便捷。
通过排队论模型,可以确定货架的最佳布局和库存管理策略,从而提高仓库的货物流动效率。
3.4 仓库入库和出库设备排队系统在物流仓储中,入库和出库设备的排队和运行情况对仓库整体效率有着重要影响。
排队论可以帮助我们评估设备使用率和效率,并优化设备的运行策略,提高仓库的物流处理能力。
第四章:排队论在物流仓储中应用案例分析4.1 ABC物流仓库的收货排队系统优化通过对ABC物流仓库的收货排队系统进行分析和优化,减少货物排队时间和仓库运营成本,提高仓库的服务水平和效益。
(完整)排队论
5。
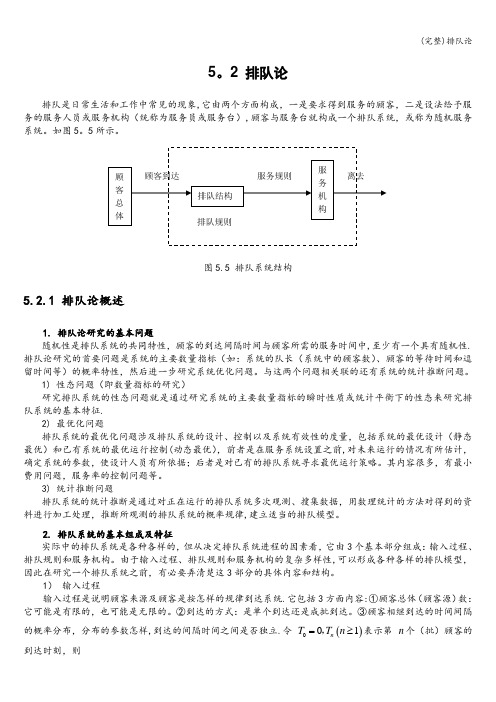
2 排队论排队是日常生活和工作中常见的现象,它由两个方面构成,一是要求得到服务的顾客,二是设法给予服务的服务人员或服务机构(统称为服务员或服务台),顾客与服务台就构成一个排队系统,或称为随机服务系统。
如图5。
5所示。
图5.5 排队系统结构5.2.1 排队论概述1. 排队论研究的基本问题随机性是排队系统的共同特性,顾客的到达间隔时间与顾客所需的服务时间中,至少有一个具有随机性.排队论研究的首要问题是系统的主要数量指标(如:系统的队长(系统中的顾客数)、顾客的等待时间和逗留时间等)的概率特性,然后进一步研究系统优化问题。
与这两个问题相关联的还有系统的统计推断问题。
1) 性态问题(即数量指标的研究)研究排队系统的性态问题就是通过研究系统的主要数量指标的瞬时性质或统计平衡下的性态来研究排队系统的基本特征.2) 最优化问题排队系统的最优化问题涉及排队系统的设计、控制以及系统有效性的度量,包括系统的最优设计(静态最优)和已有系统的最优运行控制(动态最优),前者是在服务系统设置之前,对未来运行的情况有所估计,确定系统的参数,使设计人员有所依据;后者是对已有的排队系统寻求最优运行策略。
其内容很多,有最小费用问题,服务率的控制问题等。
3) 统计推断问题排队系统的统计推断是通过对正在运行的排队系统多次观测、搜集数据,用数理统计的方法对得到的资料进行加工处理,推断所观测的排队系统的概率规律,建立适当的排队模型。
2. 排队系统的基本组成及特征实际中的排队系统是各种各样的,但从决定排队系统进程的因素看,它由3个基本部分组成:输入过程、排队规则和服务机构。
由于输入过程、排队规则和服务机构的复杂多样性,可以形成各种各样的排队模型,因此在研究一个排队系统之前,有必要弄清楚这3部分的具体内容和结构。
1) 输入过程输入过程是说明顾客来源及顾客是按怎样的规律到达系统.它包括3方面内容:①顾客总体(顾客源)数:它可能是有限的,也可能是无限的。
xiuguo_排队论

去。具体说来,大致有三种:
① 队长有限。当排队等待服务的顾客人数超过规定 数量时,后来的顾客就自动离去,另求服务,即系统 的等待空间是有限的。例如最多只能容纳 K个顾客在系 统中,当新顾客到达时,若系统中的顾客数(又称为队 长)小于 K ,则可进入系统排队或接受服务;否则,便 离开系统,并不再回来。如水库的库容是有限的,旅 馆的床位是有限的。
1.基 本 概 念
(2)顾客到达方式。这是描述顾客是怎样来到系统的, 他们是单个到达,还是成批到达。病人到医院看病是顾 客单个到达的例子。在库存问题中如将生产器材进货或 产品入库看作是顾客,那么这种顾客则是成批到达的。 (3)顾客流的概率分布,或称相继顾客到达的时间间 隔的分布。这是求解排队系统有关运行指标问题时,首 先需要确定的指标。这也可以理解为在一定的时间间隔 内到达K个顾客(K=1、2、)的概率是多大。顾客流的概 率分布一般有定长分布、二项分布、泊松流(最简单流)、 爱尔朗分布等若干种。
1.基 本 概 念
2.服务规则。这是指服务台从队列中选取顾客进行
服务的顺序。一般可以分为损失制、等待制和混合制等3
大类。 (1)损失制。这是指如果顾客到达排队系统时,所有 服务台都已被先来的顾客占用,那么他们就自动离开系 统永不再来。典型例子是,如电话拔号后出现忙音,顾
客不愿等待而自动挂断电话,如要再打,就需重新拔号,
前
言
排队是我们在日常生活和生产中经常遇到的现象。 上、下班搭乘公共汽车; 顾客到商店购买物品; 病员到医院看病;
旅客到售票处购买车票;
学生去食堂就餐等就常常出现排队和等待现象。 除了上述有形的排队之外,还有大量的所谓“无形”
排队现象,如几个顾客打电话到出租汽车站要求派车,如
数学建模排队论讲解

简介
排队论(Queuing Theory),又称随机服务系统理论 (Random Service System Theory),是一门研究拥挤 现象(排队、等待)的科学。具体地说,它是在研究 各种排队系统概率规律性的基础上,解决相应排队 系统的最优设计和最优控制问题。
目录
§1 排队系统综述及常用分布 §2 单服务台 M / M /1排队模型 §3 多服务台 M / M / C 排队模型 §4 排队系统的优化问题
负指数分布的概率密度为: fT (t) ? ? e? ? t (t ? 0)
间隔时间 T 的期望值:
E (T ) ? 1
?
1.5 排队系统的常用分布
同样,对顾客服务时间常用的概率分布也是负指数分布,
概率密度为: f (t) ? ? e?? t (t ? 0)
其中? 表示单位时间内完成服务的顾客数,也称平均服务率.
1)顾客源 ——可以是有限的,也可以是无限的.
2)顾客到达的方式——描述顾客是怎样来到系统的,是单个 到达还是成批到达.
3)顾客流的概率分布——或称相继顾客到达的时间间隔的分 布,相继到达的时间间隔可以是确定的也可以是随机的, 常见的分布有定长分布、二项分布和负指数分布等.
1.2 排队系统的组成
排队规则:指从队列中挑选顾客进行服务的规律.
多有一个顾客到达系统.即在时间 ?
t
?
?
t内有2个或2个以上顾客
? 到达的概率极小,有 lim Pn ?t ? ? t ?? 0 ?t? 0
n? 2
可以证明,在长为t的时间内到达个顾客的概率为:
Pn ?t ??
(? t) n e? ?t
n!
?t ? 0 ? n ? 0,1,2,?
运筹学课件:排队论总结

Operation Research
模型二:不允许缺货,生产需一定时间(1)
第八讲
该模型最早用于确定生产批量,因此也称为生产批量模型 (Production lot size)
模型假设条件
缺货费用无穷大,C2→∞
存储量随时间的变化情况
-R
Operation Research
第八讲
模型一:不允许缺货,备货时间很短(2)
问题分析
决策的要素: 确定合适的订货时间间隔;确定合适的订货量;
矛盾所在
1. 订货间隔时间短,可以减少每次的订货量,降低存储费用;但在一 个固定时间段内,必然会增加订购次数,使订购费用增加;
第八讲
模型四:允许缺货(需补足缺货),生产需一定时间(2)
存储量随时间的变化情况
Operation Research
解释
第八讲
Operation Research
第八讲
模型四:允许缺货(需补足缺货),生产需一定时间(3)
公式推导
Operation Research 求最小值
第八讲
Operation Research
单位时间内单位缺货的损失,C2为常数
当存货降至零时,允许拖一段时间,然后订货就逐步均匀到货, 到货(生产)速率为P为常数
需求是连续的、均匀的,设需求的速率R(单位时间的需求量)为 常数,并且P>R,则t时间的需求量为Rt
每次订货量不变,订购费不变,C3为常数 单位存储费不变,C1为常数
Operation Research
Operation Research
第八讲
第九章 排队论 (1)PPT课件

9.1排队论的基本概念
排队论是通过对服务对象到来及服务时 间的统计研究,得出这些数量指标(等 待时间、排队长度、忙期长短等)的统 计规律,然后根据这些规律来改进服务 系统的结构或重新组织被服务对象,使 得服务系统既能满足服务对象的需要, 又能使服务机构的费用最经济或某些指 标最优。
4
9.1.1排队过程的一般表示
第9章 排队论
1
整体概述
概况一
点击此处输入相关文本内容 点击此处输入相关文本内容
概况二
点击此处输入相关文本内容 点击此处输入相关文本内容
概况三
点击此处输入相关文本内容 点击此处输入相关文本内容
2
排队是我们在日常生活中经常遇到的现象,例如 病人到医院看病、客户到银行汇款、城市拥堵 路段的汽车排队、电话占线等。排队现象产生 的原因之一是要求服务的数量超过了服务机构 的容量,也就是有部分的服务对象不能立即得 到服务;原因之二是系统服务对象到达和服务 时间均存在随机性。前者可以通过增加服务机 构的容量来解决排队现象,但无休止地增加服 务机构的容量会导致追加投资并可能发生系统 资源长时间闲置。后者,也就是系统服务对象 到达和服务时间均存在随机性,致使无法准确 预测估算排队拥堵的具体情况。所以,在服务 系统中3 的排队现象几乎不可避免。
当k=1时爱尔朗分布就是负指数分布;当 k增加时,爱尔朗分布逐渐变为对称的。 当k>30时,爱尔朗分布近似于正态分布。
18
G:一般随机分布。 例如M/M/l表示到达的间隔时间服从负指数 分布,服务时间也服从负指数分布的单服务 台排队系统模型。M/D/2表示到达间隔时间 服从负指数分布,而服务时间为定长分布的 双服务台排队系统模型。
D1
L
E
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2章存储论与存储控制(ITS)2.1 模块简介2.2 确定需求存储模型(EOQ)2.2.1 基本EOQ模型求解2.2.2 允许缺货及时补充EOQ模型求解2.2.3 在制品EOQ模型2.3 有价格折扣的EOQ模型第3章排队论(QUEUING ANALYSIS)3.1 简单排队系统M/M第1章WinQSB简介1.1 实验平台、环境和主要功能QSB是Quantitative Systems for Business的缩写,WinQSB是QSB的Windows版本,是一种教学软件,里面有大量的模型,对于非大型的问题一般都能计算,较小的问题还能演示中间的计算过程。
可以在Windows9X/ME/NT/2000/XP及以上平台下运行。
WinQSB V1.0共有19个子系统,分别用于解决运筹学不同方面的问题,详见表1-1。
表1-1 WinQSB主要模块与应用范围1.2 软件安装•WinQSB的安装比较简单。
双击Setup.exe,弹出窗口如图1-1所示:图1-1•输入要安装到哪个目录,点Continue按钮,弹出窗口如图1-2所示:图1-2•输入用户名和公司或组织名称,点Continue按钮进行文件的复制,完成后弹出窗口如图1-3:图1-3显示安装完成,点“确定”退出。
WinQSB软件安装完毕后,会在开始程序WinQSB中生成19个菜单项,分别对应运筹学的19个问题。
如图1-4所示:抽样分析 综合计划编制 决策分析 动态规划 设备场地布局 预测和线性回归 目标规划存储论与存储控制系统 作业调度、编制工作进度表 线性和整数规划 马尔柯夫过程 物料需求计划 网络模型 非线性规划计划评审技术与关键路线法 二次规划 质量控制图 排队论图 1-4 针对不同的问题,选择不同的子菜单项,运行相应的程序,然后使用File 菜单下的New Problem 菜单来输入所需数据。
1.3 运行WinQSB 基本上有三种窗口:启动窗口、数据输入窗口、结果输出窗口。
现以Linear and Integer Programming 为例加以说明: 1.启动窗口。
在开始菜单中选择Linear and Integer Programming ,运行后出现启动窗口如下图 1-5 所示:标题栏今 菜单栏今 工具栏今信息栏今(1)标题栏:显示了程序的名称。
图 1-5 启动窗口(2)菜单栏:共有两个菜单:File 和Help 。
File 菜单只有三个子菜单:New Problem 、Load Problem 和Exit 。
New Problem :创建新问题Load Problem :装载问题 Exit :退出Help 菜单为帮助菜单(略)(3)工具栏:提供了执行菜单栏各功能的快捷按钮。
(4)信息栏:把鼠标移动到工具栏按钮上时,信息栏会给出相应的说明信息。
2.数据输入窗口:在File 菜单中选择New Problem 菜单(或在工具栏上按新建按钮),出现对话框 如图 1-6所示:图 1-6 参数设置对话框注意:对应于不同的子程序,弹出对话框的内容是不同的。
点击OK 按钮,进入数据输入窗口。
如图 1-7所示:图 1-7 数据输入窗口(1)菜单栏:共有9个菜单:File 、Edit 、Format 、Solve and Analysis 、Results (此处为灰色不 可用)、Utilities 、Window 、WinQSB 和Help 。
File 菜单:共有9个子菜单,如图 1-8。
新建问题今 装载问题今 关闭问题今 保存问题今 问题另存今 打印问题今打印字体今 打印设置今Edit 菜单,如图 1-9图 1-8 文件菜单剪切今 复制今 粘贴今 清除今恢复今问题名称今 变量名称今 约束名称今 目标准则今插入变量今 删除变量今图1-9 编辑菜单 需要注意的是除了剪切复制等的第一部分和Undo 的第二部分外,其它部分的子菜单会由于所选 程序的不同而不同。
具体见后面实验中各问题的详细解法。
Format 菜单,如图 1-10数字格式今字体今 对齐方式今调整行高今 调整列宽今输入格式转换开关今 输入格式转换开关今图 1-10 格式菜单Number :选择数字的显示格式。
选择此菜单,弹出窗口如图 1-11默认今 普通今 标准(带千分位) 今 货币(人民币)今 固定(2位小数)今 科学度数今图 1-11 数字格式选择框 Font :选择显示字体(为Windows 标准的字体对话框) Alignment :电子表格文字的对齐方式。
选择此菜单,弹出窗口如图1-12对齐方式 ◎左对齐○右对齐 ○居 中 应用范围 ◎所有列 ○第1行 ○第1列 ○所选列图 1-12 对齐方式选择框Row height :调节电子表格行高(如图 1-13)。
○如左流动条◎默认行高 ○最适合行高应用范围 ◎所有行 ○所选行 ○第1行图 1-13 调整行高 Columnweight :调节电子表格列宽(方法同调整行高)。
根据子程序的不同,Format 菜单中会有不同的子菜单。
具体见后面各问题的详细解法。
Solve and Analysis 菜单,如图 1-14。
图 1-14 求解与分析菜单它也会根据不同的子程序而有不同的子菜单,主要的是: Solve the Problem :求解问题Solve and Display Steps :求解并显示过程 Utility 菜单此菜单较简单,主要是提供了几个小工具,有Calculator (计算器)、Clock (时钟)和Graph/Chart (图表)。
Window 菜单,如图 1-15图 1-15 窗口菜单 此处会显示已经打开的子窗口的名称,可方便的进行切换。
Cascade :层叠,各子窗口的显示如图 1-16所示:图 1-16 窗口层叠Title :平铺,各子窗口的显示如图 1-17所示:WinQSB 菜单图 1-17 窗口平铺WinQSB 菜单提供了WinQSB 的19个功能的菜单,可在此处方便的打开其它子程序。
Help 菜单提供了WinQSB 的帮助。
(2)工具栏:此处提供了比启动窗口更丰富的工具按钮。
(3)主窗口:在此处输入具体问题的数据。
3.结果输出窗口:在输入了数据之后,选择Solve and Analysis 菜单下的Solve the Problem 菜单, 问题求解后弹出结果输出窗口如图 1-18所示:图1-18 结果输出窗口(1)此窗口有6个菜单:File、Format、Result、Utilities、Window和Help。
File菜单,如图1-19打印快速打印结果另存复制到剪贴板打印字体设置打印设置Result菜单退出图1-19 文件菜单主要是对问题进行各种不同的分析和显示。
根据不同的子程序会有所不同Format、Utilities、Window和Help菜单同数据输入窗口中的菜单。
(2)工具栏:提供了命令的快捷按钮。
(3)结果显示窗口:把问题的计算结果以表格或图形的形式显示出来。
1.4 WinQSB与Excel表格交换数据(1)从Excel表格中复制数据到winQSB:先选中Excel中要复制的数据区域,点击复制或按“Ctrl+C”键,然后在winQSB的电子表格编辑状态下选中要粘贴的单元格(选中的粘贴区域与在Excel中复制时选中的区域行列数相同),点击粘贴或按“Ctrl+V”键完成复制。
(2)把WinQSB数据输入窗口中的数据复制到Excel表格:先清空剪贴板(可用Excel中Edit菜单下的office剪贴板来清空,方法:编辑/office剪切板/全部清空),然后在WinQSB表格中选中要复制的数据,选Edit菜单下的Copy,然后在Excel表格中复制即可。
第2章存储论与存储控制(ITS)2.1 模块简介存储论与存储控制(Inventory Theory and System)模块的启动程序是:开始/程序/WinQSB/Inventory Theory and System/File/New Problem,启动后弹出如下类型选项对话框:存储类型:确定需求存储模型确定需求允许折扣问题分析单时期随机需求存储问题多时间动态需求存储问题连续需求安全库存固定订货存储系统(s, Q)连续需求安全库存库存受限存储系统(s, S)定期订货模型(R, S)混合模型(R, s, S)问题标题(可省略)时间单位(year, maths, week, day, hour, min等)图2-1 存储类型选项对话框在上述模型中,确定需求存储模型(Deterministic Demand Economic Order Quantity[EOQ] Problem),适用于模型Ⅰ(基本EOQ)、模型Ⅱ(在制品EOQ)、模型Ⅲ(允许缺货EOQ)、模型Ⅳ(允许缺货在制品EOQ);确定需求允许折扣存储模型(Deterministic Demand Quantily Duxcount Analysis Problem),适用于教材中模型Ⅴ(价格折扣EOQ);单时期随机需求存储问题适用于教模型Ⅵ(离散型随机需求,即报童问题)、模型Ⅶ(连续型随机需求)。
2.2 确定需求存储模型(EOQ)程序启动:开始/程序/WinQSB/Inventory Theory and System/File/New Problem/选择第1个单选按钮,调整时间单位,单击OK,弹出数据编辑窗口(图 2-2)。
其应用条件:全年需求固定且均匀;生产能力固定且在生产期内均衡生产;若生产能力为M,则为经济订购模型,否则为在制品存储模型;若单位缺货损失为M,则为不允许存储缺货,否则为允许缺货存储模型;折扣点数省略为无折扣模型,否则为数量折扣模型。
需求量/年(时间单位由选项框输入决定)每次订货成本(或生产准备费)/次单位存储成本/年单位缺货成本/年(不允许缺货为M)单位缺货成本/次生产能力/年(经济订购量模型为M)交纳间隔期(提前时间)/年(即时到货空白)无折扣购货成本折扣点数(无折扣空白)图2-2 确定需求EOQ模型【例2.1】某文教用品商店(零售商)每年可销售10000包光电复印纸,可从复印纸制品厂(供货商)进货。
每次订货需发生订货费100元;零售商需租用库房存放复印纸,每月每包存贮费为1元;复印纸购价10元/包。
零售商:我们都是老熟人了,能否便宜点?供货商:你如果多买就可以给你让利。
零售商:如何让利呢?供货商:你一次订货300~600包,每包9.5元;一次订货超过600包(含600包括),每包9元。
假设复印纸零售价为14元,平均毛利3元,如果缺货,年平均缺货每包将产生机会损失15元/ 年。
问题:(1)若不允许缺货,且无价格折扣情况下零售商应该订货多少次?每次订货多少?并对单位存储费从12到15,步长为1进行敏感性分析;(2)若允许缺货,且无价格折扣情况下,零售商应订货多少次?每次订货多少?最大缺货量多少?(3)若不允许缺货,是否享受折扣?享受多少折扣?每次订货量多少?2.2.1 基本EOQ模型求解例2.1中第(1)个问题为不允许缺货,无价格折扣的EOQ,称为基本EOQ模型。
