人教版-数学-八年级上册-《与三角形有关的线段》习题精选1

合集下载

8年级数学人教版上册同步练习11.1与三角形有关的线段(含答案解析)

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！．如图，图中三角形的个数为（）状元笔记【知识要点】1．三角形的三边关系三角形两边的和大于第三边，两边的差小于第三边．2．三角形三条重要线段(1)高：从三角形的顶点向对边所在的直线作垂线，顶点与垂足之间的线段叫做三角形的高．(2)中线：连接三角形的顶点与对边中点的线段叫做三角形的中线．(3)角平分线：三角形内角的平分线与对边相交，顶点与交点之间的线段叫做三角形的角平分线．3．三角形的稳定性三角形具有稳定性．【温馨提示】1．以“是否有边相等”，可以将三角形分为两类：三边都不相等的三角形和等腰三角形．而不是分为三类：三边都不相等的三角形、等腰三角形、等边三角形，等边三角形是等腰三角形的一种．2．三角形的高、中线、角平分线都是线段，而不是直线或射线．【方法技巧】1．根据三角形的三边关系判定三条线段能否组成三角形时，要看两条较短边之和是否大于最长边．2．三角形的中线将三角形分成两个同底等高的三角形，这两个三角形面积相等．参考答案:1．D解析：线段AB上有5个点，线段AB与点C组成5×（5－1）÷2=10个三角形；同样，线段DE 上也有5个点，线段DE与点C组成5×（5－1）÷2=10个三角形，图中三角形的个数为20个．故选D．2．21解析：根据前边的具体数据，再结合图形，不难发现：后边的总比前边多4，若把第一个图形中三角形的个数看作是1=4－3，则第n个图形中，三角形的个数是4n－3．所以当n=6时，原式=21．3．解：填表如下：△ABC内点的个数123 (1007)构成不重叠的小三角形的个数357 (2015)解析：当△ABC内有1个点时，构成不重叠的三角形的个数是3=1×2＋1；当△ABC内有2个点时，构成不重叠的三角形的个数是5=2×2＋1；参考上面数据可知，三角形的个数与点的个数之间的关系是：三角形内有n个点时，三角形内互不重叠的小三角形的个数是2n+1，故当有3个点时，三角形的个数是3×2＋1=7；当有1007个点时，三角形的个数是1007×2＋1=2 015．4．B解析：根据题意，得8－3＜1－2a＜8＋3，即5＜1－2a＜11，解得－5＜a＜－2．故选B．5．10 解析：∵在△ABC中，三边长分别为正整数a、b、c，且c≥b≥a＞0，∴c＜a+b．∵b=4，∴a=1，2，3，4．a=1时，c=4；a=2时，c=4或5；a=3时，c=4，5，6；a=4时，c=4，5，6，7．∴这样的三角形共有1+2+3+4=10个．6．解：原不等式可化为3（x+2）＞－2（1－2x），解得x＜8．∵x是它的正整数解，∴x可取1，2，3，5，6，7．再根据三角形三边关系，得6＜x＜10，∴x=7．。

人教版八年级上册(新)数学第11章《11.1与三角形有关的线段》同步习题

人教版八年级上册（新）数学第11章《11．1与三角形有关的线段》同步习题学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列叙述中正确的是（）A ．三角形一个角的平分线与这个角的对边相交，这个角的顶点与交点之间的射线，叫做三角形的角平分线B ．连结三角形一个顶点和它对边中点的直线，叫做三角形的中线C ．从三角形一个顶点向它的对边画垂线叫做三角形的高D ．三角形的三条中线总在三角形的内部2．三角形一边上的高（）A ．必在三角形内部B ．必在三角形外部C ．必在三角形的边上D ．以上三种情况都有可能3．如图，AC BC ⊥于C ，CD AB ⊥于D ，DE BC ⊥于E ，则下列说法中错误的是（）A ．ABC ∆中，AC 是BC 边上的高B ．BCD ∆中，DE 是BC 边上的高 C ．ABE ∆中，DE 是BE 边上的高D ．ACD ∆中，AD 是CD 边上的高 4．根据定义，三角形的角平分线，中线和高线都是（）A ．直线B ．线段C ．射线D ．以上都对 5．如果一个三角形的三条高的交点恰好是这个三角形的一个顶点，那么这个三角形是（）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不能确定 6．下列画出ABC ∆的高正确的是（）A ．AB ．BC ．CD ．D二、填空题 7．如图，则图中共有______个三角形，它们分别是______；在ABD ∆中B 所对的边是______；若BC CD DE ==，则AC 和AD 分别是______、______的中线.8．如果一个三角形两边上的高所在的直线的交点在三角形的外部，那么这个三角形是_____三角形.9．已知：如图，AC 为ABD ∆的角平分线，AE 为ADF ∆的角平分线，则有，BAC ∠=∠________；12DAE ∠=∠_______.10．已知：如图，H 是ABC ∆三条高AD 、BE 、CF 的交点，则ABC ∆中BC 边上的高是______，AHB ∆中AB 边上的高是_______，HFB ∆中BF 边上的高是________.11．如图，AD 是ABC 的中线，AE 是ADC 的中线，则有CE =______CD =_____BC .12．如图，AD BC ⊥于D ，则以AD 为高的三角形有_____个，分别是______.13．三角形的三条角平分线在三角形的________部.三、解答题14．完成下列证明过程：已知：AF ，BE ，CD 相交于O 点，并且知OC 为ABO ∆的角平分线.求证：OD 为EFO ∆的角平分线证明：∵OC 为ABO ∆的角平分线（）∴ AOC ∠=∠________（三角形角平分线定义）又∵ AOC DOF ∠=∠，BOC ∠=∠______（）∴ EOD DOF ∠=∠∴ OD 为EFO ∆的角平分线（三角形角平分线定义）15．如图，B 、D 、E 、C 在同一条直线上，过A 点画出ABE ∆，ABD ∆，ABC ∆的高，说出它们之间的关系.参考答案1．D【解析】选项A，三角形一个内角的平分线与它的对边相交，这个角的顶点与交点之间的线段叫做三角形的角平分线，A错.选项B, 三角形中，连接一个顶点和它所对边的中点的线段叫做三角形的中线.B错.选项C, 从三角形一个顶点向它的对边作一条垂线，三角形顶点和垂足之间的线段称三角形这条边上的高.C错误.D正确.所以选D.点睛：2．D【解析】锐角三角形所有高在内部，直角三角形两条高在边上，钝角三角形两条高在外部. 选D.3．C【解析】ABE ∆中，AC 是BE 边上的高,C 错.4．B【解析】三角形的角平分线，中线和高线都是线段.所以选B.5．B【解析】试题分析：因为直角三角形的三条高线的交点是直角顶点，而其他三角形三条高线的交点都不在顶点上，所以如果一个三角形的三条高的交点恰好是这个三角形的一个顶点，那么这个三角形是直角三角形．故选B ．点睛：本题考查的是三角形高的性质，熟知直角三角形的三条高的交点恰好是三角形的一个顶点是解答此题的关键．6．D【解析】钝角三角形的高在三角形外.所以选D.7．6 ABC ∆，ACD ∆，ADE ∆，ABD ∆，ACE ∆，ABE ∆ AD ACE ∆ ABD ∆【解析】(1)1+2+3=6.(2) 它们分别是ABC ∆，ACD ∆，ADE ∆，ABD ∆，ACE ∆，ABE ∆ .在ABD ∆中B ∠所对的边是AD ；若BC CD DE ==，则AC 和AD 分别是ACE ∆、ABD ∆的中线8．钝角【解析】钝角三角形的高在三角形外部.9．CAD DAF【解析】AC 为ABD ∆的角平分线, BAC CAD ∠=∠, AE 为ADF ∆的角平分线,1 2DAE DAF ∠=∠. 10．AD HF HF【解析】则ABC ∆中BC 边上的高是AD ，AHB ∆中AB 边上的高是HF ，HFB ∆中BF 边上的高是HF .11．12 14【解析】由题意得12CE =，CD = 14BC . 12．6 ADC ∆，ADE ∆，ADB ∆，ABC ∆，ABE ∆，AEC ∆【解析】以AD 为高的三角形有6个，分别是ADC ∆，ADE ∆，ADB ∆，ABC ∆，ABE ∆，AEC ∆.13．内【解析】三角形的三条角平分线在三角形的内部.14．已知，BOC ，EOD ，对顶角相等【解析】试题分析：角平分线把角分成两个相等的角.试题解析：证明：∵OC 为ABO ∆的角平分线（已知）,∴ AOC ∠=∠BOC （三角形角平分线定义）,又∵ AOC DOF ∠=∠，BOC ∠=∠EOD （对顶角相等）, ∴ EOD DOF ∠=∠,∴ OD 为EFO ∆的角平分线（三角形角平分线定义）. 15．答案见解析【解析】试题分析：ABE ∆，ABD ∆，ABC ∆的高都是AE . 试题解析：图略.ABE ∆，ABD ∆，ABC ∆的高都是AE .点睛：三角形的高以及性质锐角三角形：3条高，3条都在三角形内部，交点在三角形内部. 直角三角形：3条高，1条在三角形内部，交点在三角形内部.钝角三角形：3条高，1条在三角形内部，无交点，但是延长线交于一点，在三角形外部.。

八年级数学上册《第十一章与三角形有关的线段》同步练习题及答案-人教版

八年级数学上册《第十一章与三角形有关的线段》同步练习题及答案-人教版学校:___________班级：___________姓名：___________考号：___________一、单选题1．已知三角形两条边的长分别为3、7，则第三条边的长可以是 ( )A．3 B．10 C．11 D．72．长为9、6、4、3的四根木条，选其中三根组成三角形，共有（）种选法.A．1种B．2种C．3种D．4种3．如图，小明用铅笔可以支起一张质地均匀的三角形卡片，则他支起的这个点应是三角形的（）A．三边高的交点B．三条角平分线的交点C．三边垂直平分线的交点D．三边中线的交点4．木匠师傅在做完门框后，为防止门框变形，常象如图的方式斜拉两个木条，这样做的数学道理（）A．两点之间线段最短B．三角形的稳定性C．矩形的四个角时直角D．长方形的对称性5．如图，在△ABC中，2BD=3DC，E是AC的中点，如S△ABC=10，则S△ADE=( )A．5 B．4 C．3 D．26．如图，在平行四边形ABCD中，对角线AC,BD的长度分别为10和6，则AB长度的最大整数值是（）A．8 B．5 C．6 D．77．如图，用四个螺丝将四条不可弯曲的木条围成一个木框（形状不限），不计螺丝大小，其中相邻两螺丝的距离依次为3、4、5、7，且相邻两木条的夹角均可调整．若调整木条的夹角时不破坏此木框，则任意两个螺丝间的距离的最大值为（）A．6 B．7 C．8 D．98．如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE 的中点，且△ABC的面积为4cm2，则△BEF 的面积等于（）A．2cm2B．1cm2C．0.5 cm2D．0.25 cm2二、填空题9．三角形木架的形状不会改变，这说明三角形具有．10．已知a、b、c是△ABC的三边，化简|a﹣b﹣c|+|b+c﹣a|+|c+a+b|得．11．如图，在△ABC中，点D.E.F分别是线段BC、AD、CE的中点，且S△ABC = 8cm2，则S△BEF = cm212．如图，在△ABC中，E为AC的中点，点D为BC上一点，BD：CD=2：3，AD、BE交于点O，若S△AOE﹣S△BOD=1，则△ABC的面积为．13．在△ABC中，点D，E分别在AB，AC上，且CD与BE相交于点F，已知△BDF的面积为6，△BCF的面积为9，△CEF的面积为6，则四边形ADFE的面积为．三、解答题14．已知点O(0，0)，B(1，2)，点A在坐标轴上，且S△OAB=2，试求出所有满足条件的点A的坐标．15．已知等腰三角形的三边长分别为a+1，2a，5a－2，求这个等腰三角形的周长．16．如图，A（﹣1，0），C（1，4），点B在x轴上，且AB=3．（1）求点B的坐标；（2）求△ABC的面积；（3）在y轴上是否存在点P，使以A、B、P三点为顶点的三角形的面积为10？若存在，请直接写出点P的坐标；若不存在，请说明理由．17．如图，ABCD是凸四边形，AB=2，BC=4，CD=7，求线段AD的取值范围．18．一个三角形的三边长分别是a、a+2、a+4它的周长不超过30，求a的取值范围. 19．如图，在△ABC中，AD⊥BC于D，AE平分∠BAC．（1）若∠C=70°，∠B=40°，求∠DAE的度数（2）若∠C﹣∠B=30°，则∠DAE= ．（3）若∠C﹣∠B=α（∠C＞∠B），求∠DAE的度数（用含α的代数式表示）．参考答案1．D2．B3．D4．B5．D6．D7．D8．B9．稳定性10．3c+a﹣b11．212．1013．2414．解：若点A在x轴上，则S△OAB= 12OA×2=2解得OA=2所以点A的坐标为(2，0)或(-2，0)．若点A在y轴上，则S△OAB= 12OA×1=2，解得OA=4所以点A的坐标为(0，4)或(0，-4)．综上所述，点A的坐标为(2，0)或(-2，0)或(0，4)或(0，-4)．15．解：⑴当a+1=2a时，得a=1,三边长分别为2,2,3；周长为7⑵当a+1=5a-2时，得a= 34,三边长分别为74,74,32；周长为5.⑶当5a-2=2a时，得a= 23,三边长分别为43，43，53；周长为133.所以这个等腰三角形的周长为7,5，或13316．解：（1）点B在点A的右边时，﹣1+3=2 点B在点A的左边时，﹣1﹣3=﹣4所以，B的坐标为（2，0）或（﹣4，0）；（2）△ABC的面积=12×3×4=6；（3）设点P到x轴的距离为h则12×3h=10解得h=203点P 在y 轴正半轴时，P （0，203）点P 在y 轴负半轴时，P （0，﹣203）综上所述，点P 的坐标为（0，203）或（0，﹣203）．17．解：连接AC ．∵AB=2，BC=4在△ABC 中，根据三角形的三边关系，4﹣2＜AC ＜2+4，即2＜AC ＜6． ∴﹣6＜﹣AC ＜﹣2，1＜CD ﹣AC ＜5，9＜CD+AC ＜13在△ACD 中，根据三角形的三边关系，得CD ﹣AC ＜AD ＜CD+AC ∴1＜AD ＜13．故AD 的取值范围是1＜AD ＜13．18．解：由题意得 {a +a +2>a +4a +a +2+a +4≤30解得 2<a ≤8 .∴a 的取值范围是 2<a ≤8 .19．（1）解：由已知可得，∠BAC=180°﹣40°﹣70°=70° ∴∠CAD=20°∴∠DAE=∠CAE﹣∠CAD=35°﹣20°=15°；（2）15°（3）解：∵∠B﹣∠C=α∴∠DAE= 12×α= 12α。

人教版八年级上册数学：11.1 与三角形有关的线段练习卷

人教版八年级上册数学：11.1 与三角形有关的线段练习卷与三角形有关的线段一、填空题:1、如图，在△ABC中，已知点D、E、F分别是边BC、AD、CE 上的中点，且S△ABC=4，则S△BFF=_______2、△ABC的三边长分别为，则__.3、三角形的三边长分别为5，1+2x，8，则x的取值范围是 .4、在△ABC中，点D，E分别在AB，AC上，且CD与BE相交于点F，已知△BDF的面积为6，△BCF的面积为9，△CEF的面积为6，则四边形ADFE的面积为 .5、如图，△ABC的三个顶点和它内部的点P1，把△ABC分成3个互不重叠的小三角形；△ABC的三个顶点和它内部的点P1、P2，把△ABC分成5个互不重叠的小三角形；△ABC的三个顶点和它内部的点 P1、P2、P3，把△ABC分成7个互不重叠的小三角形；…△ABC的三个顶点和它内部的点 P1、P2、P3、…、P2019，把△ABC分成个互不重叠的小三角形.6、如图，D，E分别是△ABC边AB，BC上的点，AD=2BD，BE=CE，设△ADF的面积为S1，△FCE的面积为S2，若S△ABC=6，则S1－S2的值为_________.二、选择题：7、如图AD⊥BC于点D，那么图中以AD为高的三角形有个（）A.2条B.3条C.4条 D.5条13、已知一个三角形的两边长分别是2和7，第三边为偶数，则此三角形的周长是（）A.15B.16C.17D.15或1714、现有3cm，4cm，7cm， cm长的四根木棒，任取其中三根组成一个三角形，那么可以组成的三角形的个数是( )A.1个B.2个C.3个D.4个15、下列说法不正确的是（）A.三角形的中线在三角形的内部B.三角形的角平分线在三角形的内部C.三角形的高在三角形的内部D.三角形必有一高线在三角形的内部16、一个三角形的两边长为3和7，第三边长为偶数，则第三边为（）A.6B.6或8 C.4 D.4或617、画△ABC的边AB上的高，下列画法中，正确的是（）A. B. C. D.18、设△ABC的面积为1，如图①将边BC、AC分别2等份，BE1、AD1相交于点O，△AOB的面积记为S1；如图②将边BC、AC分别3等份，BE1、AD1相交于点O，△AOB的面积记为S2；……，依此类推，则S5的值为（）A. B. C. D.三、解答题:19、如图，每个小正方形的边长为1，在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点B的对应点B′.根据下列条件，利用网格点和三角板画图：（1）补全△A′B′C′（2）画出AB边上的中线CD；（3）画出BC边上的高线AE；（4）△A′B′C′的面积为 .20、已知a、b、c是三角形的三边长，①化简：|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a﹣b|；②若a+b=11，b+c=9，a+c=10，求这个三角形的各边.21、如图，在△ABC中，AB=AC，AC边上的中线BD把△ABC 的周长分成12cm和15cm两部分，求△ABC各边的长.22、已知△ABC的面积是60，请完成下列问题：（1）如图1，若AD是△ABC的BC边上的中线，则△ABD的面积_______△ACD的面积（填“＞”“＜”或“=”）（2）如图2，若CD、BE分别是△ABC的AB、AC边上的中线，求四边形ADOE的面积可以用如下方法：连接AO，由AD=DB得：S△ADO=S△BDO，同理：S△CEO=S△AEO，设S△ADO=x，S△CEO=y，则S△BDO=x，S△AEO=y由题意得：S△ABE=S△ABC=30，S△ADC=S△ABC=30，可列方程组为：，解得_______，通过解这个方程组可得四边形ADOE的面积为_______.（3）如图3，AD：DB=1：3，CE：AE=1：2，请你计算四边形ADOE的面积，并说明理由.23、如图1，在Rt△ABC中，∠ACB=90°，D是AB上一点，且∠ACD=∠B；（1）求证：CD⊥AB，并指出你在证明过程中应用了哪两个互逆的真命题；（2）如图2，若AE平分∠BAC，交CD于点F，交BC于E.求证：∠AEC=∠CFE；（3）如图3，若E为BC上一点，AE交CD于点F，BC=3CE，AB=4AD，△ABC、△CEF、△ADF的面积分别为S△ABC、S△CEF、S △ADF，且S△ABC=36，则S△CEF﹣S△ADF= .（仅填结果）参考答案1、答案为：12、答案为：3、答案为：1＜x＜6.4、答案为：24.5、答案为：4035.6、答案为：17、D8、A9、C10、A11、C12、C。

人教版数学八年级上册11.1与三角形有关的线段练习 (含答案)

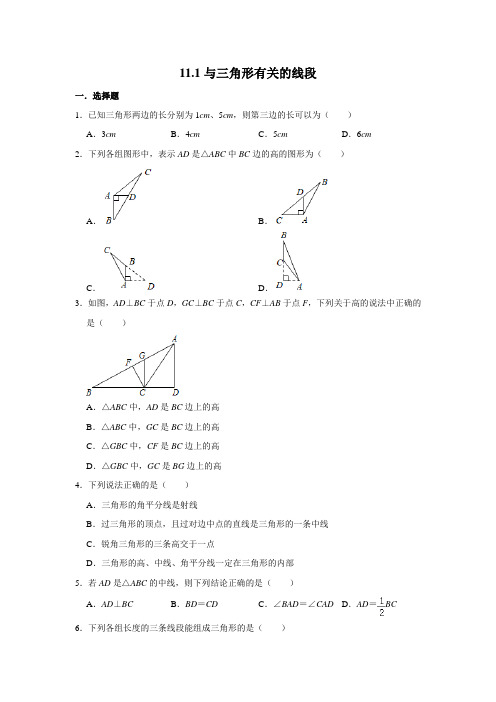
11.1与三角形有关的线段一．选择题1．已知三角形两边的长分别为1cm、5cm，则第三边的长可以为（）A．3cm B．4cm C．5cm D．6cm2．下列各组图形中，表示AD是△ABC中BC边的高的图形为（）A．B．C．D．3．如图，AD⊥BC于点D，GC⊥BC于点C，CF⊥AB于点F，下列关于高的说法中正确的是（）A．△ABC中，AD是BC边上的高B．△ABC中，GC是BC边上的高C．△GBC中，CF是BC边上的高D．△GBC中，GC是BG边上的高4．下列说法正确的是（）A．三角形的角平分线是射线B．过三角形的顶点，且过对边中点的直线是三角形的一条中线C．锐角三角形的三条高交于一点D．三角形的高、中线、角平分线一定在三角形的内部5．若AD是△ABC的中线，则下列结论正确的是（）A．AD⊥BC B．BD＝CD C．∠BAD＝∠CAD D．AD＝BC 6．下列各组长度的三条线段能组成三角形的是（）A．4cm，5cm，9cm B．4cm，4cm，8cmC．5cm，6cm，7cm D．3cm，5cm，10cm7．如果a、b、c分别是三角形的三条边，那么化简|a﹣c+b|+|b+c﹣a|的结果是（）A．﹣2c B．2b C．2a﹣2c D．b﹣c8．如图，在△ABC中，AB＝2020，AC＝2018，AD为中线，则△ABD与△ACD的周长之差为（）A．1B．2C．3D．49．如图，△ABC的BC边上的高是（）A．BE B．AF C．CD D．CF10．设三角形三边之长分别为3，8，1﹣2a，则a的取值范围为（）A．3＜a＜6B．﹣5＜a＜﹣2C．﹣2＜a＜5D．a＜﹣5或a＞2二．填空题11．如图，根据“两点之间线段最短”，可以判定AC+BC AB（填“＞”“＜”或“＝”）．12．从长度分别为3cm，4cm，5cm，6cm，9cm的线段中任意取3条，能构成的三角形个数为．13．△ABC的两边长分别是2和7，且第三边为奇数，则第三边长为．14．如图，AD是△ABC的一条中线，若BD＝3，则BC＝．15．如图所示，第1个图中有1个三角形，第2个图中共有5个三角形，第3个图中共有9个三角形，依此类推，则第6个图中共有三角形个．三．解答题16．在△ABC中，已知AB＝3，AC＝7，若第三边BC的长为偶数，求△ABC的周长．17．已知a＝m2+n2，b＝m2，c＝mn，且m＞n＞0．（1）比较a，b，c的大小；（2）请说明以a，b，c为边长的三角形一定存在．18．如图，在三角形ABC中，AB＝10cm，AC＝6cm，D是BC的中点，E点在边AB上，三角形BDE与四边形ACDE的周长相等．（1）求线段AE的长．（2）若图中所有线段长度的和是53cm，求BC+DE的值．参考答案一．选择题1．解：设第三边的长为xcm，则5﹣1＜x＜1+5，即4＜x＜6．故选：C．2．解：△ABC的高AD是过顶点A与BC垂直的线段，只有D选项符合．故选：D．3．解：∵AD⊥BC于点D，∴△ABC中，AD是BC边上的高，故A选项正确，B选项错误；∵CF⊥AB于点F，∴△GBC中，CF是BG边上的高，故C选项错误，D选项错误．故选：A．4．解：A．三角形的角平分线是线段，故A不符合题意；B．三角形的中线是线段，故B不符合题意；C．锐角三角形的三条高交于一点说法正确，故C符合题意；D．锐角三角形的三条高都在三角形内部；直角三角形有两条高与直角边重合，另一条高在三角形内部；钝角三角形有两条高在三角形外部，一条高在三角形内部．故D不符合题意；故选：C．5．解：∵AD是△ABC的中线，∴BD＝DC，故选：B．6．解：根据三角形的三边关系，A、4+5＝9，不能组成三角形，不符合题意；B、4+4＝8，不能够组成三角形，不符合题意；C、5+6＞7，能组成三角形，符合题意；D、3+5＝8＜10，不能组成三角形，不符合题意．故选：C．7．解：∵a、b、c分别是三角形的三条边，∴a﹣c+b＞0，b+c﹣a＞0，∴|a﹣c+b|+|b+c﹣a|＝a﹣c+b+b+c﹣a＝2b．故选：B．8．解：∵AD为中线，∴DB＝DC，∴△ABD与△ACD的周长之差为：（AB+AD+BD）﹣（AD+DC+AC）＝AB+AD+BD﹣AD﹣DC﹣AC＝AB﹣AC＝2020﹣2018＝2，故选：B．9．解：△ABC的BC边上的高是AF，故选：B．10．解：由题意得：8﹣3＜1﹣2a＜8+3，解得：﹣5＜a＜﹣2，故选：B．二．填空题11．解：如图，根据“两点之间线段最短”，可以判定AC+BC＞AB，故答案为：＞．12．解：其中的任意三条组合有：3cm、4cm、5cm；3cm、4cm、6cm；3cm、4cm、9cm；3cm、5cm、6cm；3cm、5cm、9cm；3cm、6cm、9cm；4cm、5cm、6cm；4cm、5cm、9cm；4cm、6cm、9cm；5cm、6cm、9cm十种情况．根据三角形的三边关系，其中的3cm、4cm、5cm；3cm、4cm、6cm；3cm、5cm、6cm；4cm、5cm、6cm；4cm、6cm、9cm；5cm、6cm、9cm能搭成三角形．故答案为：6．13．解：∵7﹣2＝5，7+2＝9，∴5＜第三边＜9，∵第三边为奇数，∴第三边长为7．故答案为：7．14．解：∵AD是△ABC的一条中线，BD＝3，∴BC＝2BD＝2×3＝6．故答案为：6．15．解：第n个图形中，三角形的个数是1+4（n﹣1）＝4n﹣3．所以当n＝6时，原式＝21，故答案为：21．三．解答题16．解：∵在△ABC中，AB＝3，AC＝7，∴第三边BC的取值范围是：4＜BC＜10，∴符合条件的偶数是6或8，∴当BC＝6时，△ABC的周长为：3+6+7＝16；当BC＝8时，△ABC的周长为：3+7+8＝18．∴△ABC的周长为16或18．17．解：（1）∵a＝m2+n2，b＝m2，c＝mn，且m＞n＞0，∴m2+n2＞m2＞mn，∴a＞b＞c；（2）∵m＞n＞0，∴mn＞n2，∴m2+mn＞m2+n2，∴a，b，c为边长的三角形一定存在．18．解：（1）∵三角形BDE与四边形ACDE的周长相等，∴BD+DE+BE＝AC+AE+CD+DE，∵BD＝DC，∴BE＝AE+AC，设AE＝x cm，则BE＝（10﹣x）cm，由题意得，10﹣x＝x+6．解得，x＝2，∴AE＝2cm；（2）图中共有8条线段，它们的和为：AE+EB+AB+AC+DE+BD+CD+BC＝2AB+AC+2BC+DE，由题意得，2AB+AC+2BC+DE＝53，∴2BC+DE＝53﹣（2AB+AC）＝53﹣（2×10+6）＝27，∴BC+DE＝（cm）．。

人教版八年级上册 111 与三角形有关的线段同步练习及答案

11.1 与三角形有关的线段一、单选题1.一个三角形的两边长为3和8，第三边长为奇数，则第三边长为（）A. 5或7B. 7或9C. 7D. 92.等腰三角形的一条边长为6，另一边长为13，则它的周长为（）A. 25B. 25或32C. 32D. 193.若三角形的三边长分别为3，4，x，则x的值可能是（）A. 1B. 6C. 7D. 104.如图所示，D，E分别是△ABC的边AC ，BC 的中点则下列说法不正确的是（）A. DE是△BDC的中线B. BD是△ABC的中线C. AD=DC，BE= EC，D. 图中∠C的对边是DE5.将几根木条用钉子钉成如下的模型，其中在同一平面内不具有稳定性的是（）A. B. C. D.6.如图，AD⊥BC，垂足为D，∠BAC=∠CAD，下列说法正确的是（）A. 直线AD是△ABC的边BC上的高B. 线段BD是△ABD的边AD上的高C. 射线AC是△ABD的角平分线D. △ABC与△ACD的面积相等7.在等腰△ABC中，AB=AC，其周长为20cm，则AB边的取值范围是（）A. 1cm＜AB＜4cmB. 5cm＜AB＜10cmC. 4cm＜AB＜8cmD. 4cm＜AB＜10cm二、填空题8.若一个三角形的两边长分别为2，7，且第三边的长为奇数，则这个三角形的周长为________．9.木工师傅在做完门框后，为防止变形，常常像如图所示那样钉上两条斜拉的木板条（即图中的AB、CD 两根木条），这样做的数学道理是________.10.已知a、b、c是三角形的三边长，化简：|a﹣b+c|+|a﹣b﹣c|=________．11.已知三角形的两边长分别为3和6，那么第三边长x的取值范围是________12.已知直线l1∥l2，BC=3cm，S△ABC=3cm2，则S△A1BC的高是________．13.在△ABC中，AB=8，AC=10，则BC边上的中线AD的取值范围是________．三、解答题14.要使四边形木架（用四根木条钉成）不变形，至少要再钉上几根木条？五边形木架和六边形木架呢？n 边形木架呢？15.如图，在直角三角形ABC中，∠ACB=90°，CD是AB边上的高，AB=10cm，BC=8cm，AC=6cm，求：（1）△ABC的面积；（2）CD的长．16.在△ABC中，BC边上的高h= cm，它的面积恰好等于边长为cm的正方形面积。

人教版八年级数学上册第十一章《与三角形有关的线段》课时练习题(含答案)

人教版八年级数学上册第十一章《与三角形有关的线段》课时练习题（含答案）一、单选题1．如图，在ABC中，D、E、F分别是BC、AC、AD的中点，若ABC的面积是40，则四边形BDEF的面积是（）A．10 B．12.5C．15 D．202．下列长度的三条线段能组成三角形的是（）A．3，3，4 B．7，4，2 C．3，4，8 D．2，3，53．下列各图中，作ABC边AC上的高，正确的是（）A．B．C．D．4．已知三角形的一边长为8，则它的另两边长分别可以是（）A．2，9 B．17，29 C．3，12 D．4，45．如图，在△ABC中，AB=5，AC=8，CD=3BD，点E是AC的中点，BE、AD交于点F，则四边形DCEF的面积的最大值是（）．A ．10cm 2B ．9cm 2C ．8cm 2D ．7cm 2二、填空题 6．电工师傅在安好电线杆后，为了防止电线杆倾倒，常常按图所示引两条拉线，这样做的数学道理是______．7．如果三条线段,,a b c 可组成三角形，且3a =，4b =，c 是奇数，则c =__________． 8．如图，在四边形ABCD 中，∠B=∠C=90︒，AB=BC=2，CD=1，F 1是BC 的中点，连接AF 1，DF 1，得到△AF 1D;点F 2是CF 1的中点，连接AF 2，DF 2，得到△AF 2D ；点F 3是CF 2的中点，连接AF 3，DF 3，得到△AF 3D ；．...；按照此规律继续进行下去，则△AF n D 的面积为______.（用含正整数n 的式子表示）三、解答题9．在ABC 中，AB AC =，AC 上的中线BD 把三角形的周长分为21和12两部分，则三角形各边长为多少？10．在△ABC 中，AB ＝9，BC ＝2，AC ＝x ．（1）求x 的取值范围；（2）若△ABC 的周长为偶数，则△ABC 的周长为多少？参考答案1．C2．A3．D4．A5．B6．三角形的稳定性．7．3或58．21 2nn9．14，14，510．（1）7＜x＜11；（2）20。

八年级数学上册第十一章三角形 11.1 与三角形有关的线段习题 (新版)新人教版

11.1 与三角形有关的线段学校：___________姓名：___________班级：___________一．选择题（共15小题）1．（2018•长沙）下列长度的三条线段，能组成三角形的是（）A．4cm，5cm，9cm B．8cm，8cm，15cm C．5cm，5cm，10cm D．6cm，7cm，14cm 2．（2018•常德）已知三角形两边的长分别是3和7，则此三角形第三边的长可能是（）A．1 B．2 C．8 D．113．（2018•河北）下列图形具有稳定性的是（）4．（2017•永州）小红不小心把家里的一块圆形玻璃打碎了，需要配制一块同样大小的玻璃镜，工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A，B，C，给出三角形ABC，则这块玻璃镜的圆心是（）A．AB，AC边上的中线的交点B．AB，AC边上的垂直平分线的交点C．AB，AC边上的高所在直线的交点D．∠BAC与∠ABC的角平分线的交点5．（2017•白银）已知a，b，c是△ABC的三条边长，化简|a+b﹣c|﹣|c﹣a﹣b|的结果为（）A．2a+2b﹣2c B．2a+2b C．2c D．06．（2016•岳阳）下列长度的三根小木棒能构成三角形的是（）A．2cm，3cm，5cm B．7cm，4cm，2cm C．3cm，4cm，8cm D．3cm，3cm，4cm 7．（2015•长沙）如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（）A．B．C．D．8．（2018•遵义一模）如图，CD，CE，CF分别是△ABC的高、角平分线、中线，则下列各式中错误的是（）A．AB=2BF B．∠ACE=∠ACB C．AE=BE D．CD⊥BE9．（2018•南安市二模）长度分别为x，3，5的三条线段能组成一个三角形，x的值可以是（）A．2 B．3 C．8 D．910．（2018•杭州二模）四根长度分别为3，4，6，x（x为正整数）的木棒，从中任取三根，首尾顺次相接都能组成一个三角形，则（）A．组成的三角形中周长最小为9B．组成的三角形中周长最小为10C．组成的三角形中周长最大为19D．组成的三角形中周长最大为1611．（2017•上思县校级模拟）三条线段a，b，c长度均为整数且a=3，b=5．则以a，b，c为边的三角形共有（）A．4个B．5个C．6个D．7个12．（2017•裕华区校级模拟）如图，AD⊥BD于点D，GC⊥BC于点C，CF⊥AB于点F，下列关于高的说法中错误的是（）A．△ABC中，AD是BC边上的高B．△GBC中，CF是BG边上的高C．△ABC中，GC是BC边上的高D．△GBC中，GC是BC边上的高13．（2017•邕宁区校级模拟）如果三角形的两边长分别为3和5，则周长L的取值范围是（）A．6＜L＜15 B．6＜L＜16 C．11＜L＜13 D．10＜L＜1614．（2017•龙华区二模）已知三角形三边的长分别为1、2、x，则x的取值范围在数轴上表示为（）A．B．C．D．15．（2017•崇安区一模）如图，用四条线段首尾相接连成一个框架，其中AB=12，BC=14，CD=18，DA=24，则A、B、C、D任意两点之间的最长距离为（）A．24 B．26 C．32 D．36二．填空题（共11小题）16．（2018•泰州）已知三角形两边的长分别为1、5，第三边长为整数，则第三边的长为．17．（2017•来宾）在长度为2，5，6，8的四条线段中，任取三条线段，可构成个不同的三角形．18．（2016•金华）由6根钢管首尾顺次铰接而成六边形钢架ABCDEF，相邻两钢管可以转动．已知各钢管的长度为AB=DE=1米，BC=CD=EF=FA=2米．（铰接点长度忽略不计）（1）转动钢管得到三角形钢架，如图1，则点A，E之间的距离是米．（2）转动钢管得到如图2所示的六边形钢架，有∠A=∠B=∠C=∠D=120°，现用三根钢条连接顶点使该钢架不能活动，则所用三根钢条总长度的最小值是米．19．（2017秋•门头沟区期末）2017年11月5日19时45分，我国在西昌卫星发射中心用长征三号乙运载火箭，以“一箭双星”的方式成功发射第二十四、二十五颗北斗导航卫星．这两颗卫星属于中圆地球轨道卫星，是我国北斗三号第一、二颗组网卫星，开启了北斗卫星导航系统全球组网的新时代．如图所示，在发射运载火箭时，运载火箭的发射架被焊接成了许多的三角形，这样做的原因是：．20．（2017秋•房山区期末）若有一条公共边的两个三角形称为一对“共边三角形”，则图中以BC为公共边的“共边三角形”有对．21．（2017秋•合浦县期末）已知△ABC的三边长a、b、c，化简|a+b﹣c|﹣|b﹣a﹣c|的结果是．22．（2017秋•襄城区期末）三角形的三边长分别为5，8，2x+1，则x的取值范围是．23．（2017秋•怀柔区期末）如图，△ABC中，BC边所在直线上的高是线段．24．（2017秋•鼓楼区期末）如图，自行车的主框架采用了三角形结构，这样设计的依据是三角形具有．25．（2017秋•西城区校级期末）我们知道三角形的两边之和大于第三边，如图AB+AC＞BC，其中的道理是因为．26．（2017秋•昌平区期末）小龙平时爱观察也喜欢动脑，他看到路边的建筑和电线架等，发现了一个现象：一切需要稳固的物品都是由三角形这个图形构成的，当时他就思考，数学王国中不仅只有三角形，为何偏偏用三角形稳固它们呢？请你用所学的数学知识解释这一现象的依据为．三．解答题（共2小题）27．（2017春•尧都区期末）如图，在△BCD中，BC=4，BD=5，（1）求CD的取值范围；（2）若AE∥BD，∠A=55°，∠BDE=125°，求∠C的度数．28．（2016秋•西青区期末）如图，△ABC中，A1，A2，A3，…，A n为AC边上不同的n个点，首先连接BA1，图中出现了3个不同的三角形，再连接BA2，图中便有6个不同的三角形…（1）完成下表：（2）若出现了45个三角形，则共连接了多少个点？（3）若一直连接到A n，则图中共有个三角形．参考答案与试题解析一．选择题（共15小题）1．解：A、∵5+4=9，9=9，∴该三边不能组成三角形，故此选项错误；B、8+8=16，16＞15，∴该三边能组成三角形，故此选项正确；C、5+5=10，10=10，∴该三边不能组成三角形，故此选项错误；D、6+7=13，13＜14，∴该三边不能组成三角形，故此选项错误；故选：B．2．解：设三角形第三边的长为x，由题意得：7﹣3＜x＜7+3，4＜x＜10，故选：C．3．解：三角形具有稳定性．故选：A．4．解：由题意可得，所求的圆形玻璃是△ABC的外接圆，∴这块玻璃镜的圆心是△ABC三边垂直平分线的交点，故选：B．5．解：∵a、b、c为△ABC的三条边长，∴a+b﹣c＞0，c﹣a﹣b＜0，∴原式=a+b﹣c+（c﹣a﹣b）=a+b﹣c+c﹣a﹣b=0．故选：D．6．解：A、因为2+3=5，所以不能构成三角形，故A错误；B、因为2+4＜7，所以不能构成三角形，故B错误；C、因为3+4＜8，所以不能构成三角形，故C错误；D、因为3+3＞4，所以能构成三角形，故D正确．故选：D．7．解：为△ABC中BC边上的高的是A选项．故选：A．8．解：∵CD，CE，CF分别是△ABC的高、角平分线、中线，∴CD⊥BE，∠ACE=∠ACB，AB=2BF，无法确定AE=BE．故选：C．9．解：根据三角形的三边关系，得：2＜x＜8．∴x的值可以是3，故选：B．10．解：其中的任意三根的组合有3、4、6；3、4、x；3、6、x；4、6、x共四种情况，由题意：从中任取三根，首尾顺次相接都能组成一个三角形，可得3＜x＜7①若三边为3、4、6时，其周长为3+4+6=13；②若三边为3、4、x时，4﹣3＜x＜4+3，即3＜x＜7由于x为正整数，当x为4或5或6，其周长最小为4+3+4=11，周长最大为3+4+6=13；③若三边为3、6、x时，6﹣3＜x＜6+3，即3＜x＜7，由于x为正整数，则x为4或5或6，其周长最小为3+6+4=13，周长最大为3+6+6=15；④若三边为4、6、x时，6﹣4＜x＜6+4，即3＜x＜7由于x为正整数，则x为4或5或6，其周长最小为4+6+4=14，周长最大为4+6+6=16；综上所述，三角形周长最小为11，最大为16，故选：D．11．解：∵c的范围是：2＜c＜8，∴c的值可以是：3、4、5、6、7，共5个数，因而由a、b、c为边可组成5个三角形．故选：B．12．解：A、△ABC中，AD是BC边上的高正确，故本选项错误；B、△GBC中，CF是BG边上的高正确，故本选项错误；C、△ABC中，GC是BC边上的高错误，故本选项正确；D、△GBC中，GC是BC边上的高正确，故本选项错误．故选：C．13．解：根据三角形的三边关系，得第三边大于2，而小于8．则周长L的取值范围是大于10，而小于16．故选：D．14．解：∵三角形的三边长分别是x，1，2，∴x的取值范围是1＜x＜3，故选：A．15．解：已知AB=12，BC=14，CD=18，DA=24；①选12+14、18、24作为三角形，则三边长26、18、24；26﹣24＜18＜26+24，能构成三角形，此时两个端点间的最长距离为26；②选12、14+18、24作为三角形，则三边长为12、32、24；32﹣24＜12＜32+24，能构成三角形，此时两个端点间的最大距离为32；③选12、14、18+24作为三角形，则三边长为12、14、42；12＜42﹣14，不能构成三角形．故选：C．二．填空题（共11小题）16．解：根据三角形的三边关系，得第三边＞4，而＜6．又第三条边长为整数，则第三边是5．17．解：∵从长度分别为2，5，6，8的四条线段中任取三条，能组成三角形的有：2、5、6；5、6、8；故答案为2．18．解：（1）如图1中，∵FB=DF，FA=FE，∴∠FAE=∠FEA，∠B=∠D，∴∠FAE=∠B，∴AE∥BD，∴=，∴=，∴AE=，故答案为．（2）如图中，作BN⊥FA于N，延长AB、DC交于点M，连接BD、AD、BF、CF．在RT△BFN中，∵∠BNF=90°，BN=，FN=AN+AF=+2=，∴BF==，同理得到AC=DF=，∵∠ABC=∠BCD=120°，∴∠MBC=∠MCB=60°，∴∠M=60°，∴CM=BC=BM，∵∠M+∠MAF=180°，∴AF∥DM，∵AF=CM，∴四边形AMCF是平行四边形，∴CF=AM=3，∵∠BCM=∠CBD+∠CDB=60°，∠CBD=∠CDB，∴∠CBD=∠CDB=30°，∵∠M=60°，∴∠MBD=90°，∴BD==2，同理AE=2，∵＜3＜2，∴用三根钢条连接顶点使该钢架不能活动，∴连接AC、BF、DF即可，∴所用三根钢条总长度的最小值3，故答案为3．19．解：这样做的原因是三角形具有稳定性．故答案为：三角形具有稳定性．20．解：△BDC与△BEC、△BDC与△BAC、△BEC与△BAC共三对．故答案为：3．21．解：∵△ABC的三边长分别是a、b、c，∴a+b＞c，b﹣a＜c，∴a+b﹣c＞0，b﹣a﹣c＜0，∴|a+b﹣c|﹣|b﹣a﹣c|=a+b﹣c﹣（﹣b+a+c）=a+b﹣c+b﹣a﹣c=2（b﹣c）；故答案为：2（b﹣c）22．解：根据三角形的三边关系可得：8﹣5＜2x+1＜5+8，解得：1＜x＜6．故答案为：1＜x＜6．23．解：△ABC中，BC边所在直线上的高是线段AD，故答案为：AD24．解：自行车的主框架采用了三角形结构，这样设计的依据是三角形具稳定性，故答案为：稳定性．25．解：三角形的两边之和大于第三边，其道理是两点之间线段最短．故答案为：两点之间线段最短26．解：用三角形稳固它们是因为三角形具有稳定性，故答案为：三角形具有稳定性．三．解答题（共2小题）27．解：（1）∵在△BCD中，BC=4，BD=5，∴1＜DC＜9；（2）∵AE∥BD，∠BDE=125°，∴∠AEC=55°，又∵∠A=55°，∴∠C=70°．28．解：（1）（2）8个点；（3）1+2+3+…+（n+1）= [1+2+3+…+（n+1）+1+2+3+…+（n+1）] =（n+1）（n+2）．故答案为（n+1）（n+2）．。

人教版八年级数学上册与三角形有关的线段专题训练试题(精品测试卷)

（1）求这条直线的解析式；
（2）若该直线分别与x轴、y轴交于A．B两点,点P在x轴上,且S△PAB=6S△OAB，求点P坐标．
A.(0.5,﹣0.5)B.( , )C.(2,1)D.(1.5,0.5)
12.如图，直线y=﹣ x+8与x轴、y轴分别交于A．B两点，点M是OB上一点，若直线AB沿AM折叠，点B恰好落在x轴上的点C处，则点M的坐标是（）
A. （0，4）B. （0，3）C. （﹣4，0）D. （0，﹣3）
二、填空题:
C.AE＝BED.CD⊥BE
17.一个三角形中直角的个数最多有（）
A.3B.1C.2D. 0
18.下列图形中，不具有稳定性的是（）
A. B. C. D.
19.下列各组中三条线段能组成三角形的是（）
A.3，4，8B.5，6，11C.5，6，10D.4，4，8
20.如图所示，其中三角形个数是（）
A. B. C. D.
5.均匀地向一个容器注水，最后将容器注满在注水过程中，水的高度h随时间t的变化规律如图所示，这个容器的形状可能是
A B. C. D.
6.正比例函数y=3x的大致图像是( )
A. B. C. D.
7.已知正比例函数（ ≠0）图象如图所示，则在下列选项中值可能是（）
A.1B.2C.3D.4
二、选择题
9.已知三角形的两边长分别为4和9，则此三角形的第三边长可能为（）
A.9B.4C.5D.13
10.下列长度的三根木棒首尾相接，不能做成三角形框架的是( )
A. 5cm、7cm、2cmB. 7cm、13cm、10cm
C. 5cm、7cm、11cmD. 5cm、10cm、13cm
11.如图，已知BE，CF分别为△ABC的两条高，BE和CF相交于点H，若∠BAC=50°，则∠BHC为（）

八年级数学上册《第十一章与三角形有关的线段》同步练习题及答案(人教版)

八年级数学上册《第十一章与三角形有关的线段》同步练习题及答案（人教版) 班级姓名学号一、单选题1．以下各组线段为边，能组成三角形的是（）A．8cm，6cm，4cm B．2cm，4cm，6cmC．14cm，6cm，7cm D．2cm，3cm，6cm2．如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（）A．锐角三角形B．直角三角形C．钝角三角形D．不能确定3．下面四个图形中，线段BE是△ABC的高的图是（）A．B．C．D．4．将几根木条用钉子钉成如下的模型，其中在同一平面内不具有稳定性的是（）A．B．C．D．5．G为△ABC的重心，△ABC的三边长满足AB＞BC＞CA，记△GAB，△GBC，△GCA的面积分别为S1、S2、S3，则有（）A．S1＞S2＞S3B．S1＝S2＝S3C．S1＜S2＜S3D．S1、S2、S3的大小关系不确定6．如图，数轴上-6，-3与6表示的点分别为M、A、N，点B为线段AN上一点，分别以A、B为中心旋转MA、NB，若旋转后M、N两点可以重合成一点C（即构成△ABC），则点B代表的数可能为（）A．-1 B．0 C．2.5 D．37．如图，AD，AE分别是△ABC的高和角平分线，若∠B＝30°，∠C＝50°，则∠DAE的度数为（）A．10°B．15°C．20°D．25°8．如图，△ ABC中，AD是BC边上的中线，CE是△ ACD中AD边上的中线，如果△ ABC的面积是20，那么△ ACE的面积是（）A．10 B．6 C．5 D．4二、填空题9．已知a、b、c是一个三角形的三条边长，则化简|a－b＋c|－|a－b－c|＝10．如图，AD是ΔABC的中线，ED是ΔABD的中线，如SΔAED=5cm2，则SΔABC=cm2．11．如图，在△ABC中，已知点D，E，F分别是BC、AD、CE的中点，且三角形ABC的面积等于4cm2，则三角形BEF的面积等于cm2．12．如图所示，CD是△ABC的中线，AC=9cm，BC=3cm，那么△ACD和△BCD的周长差是cm．13．如图，∠MAB为锐角，AB＝10，点B到射线AM的距离为6，点C在射线AM上，BC＝x，若△ABC的形状、大小是唯一确定的，则x的取值范围是．三、解答题14．甲地离学校4 km，乙地离学校1 km，记甲、乙两地之间的距离为d(km)，求d的取值范围．15．如图，已知AB=AC=AD，且AD∥BC，求证：∠C=2∠D．16．如图，△ABC中，∠A=30°，∠B=62°，CE平分∠ACB，CD⊥AB于D，DF⊥CE于F，求∠CDF的度数．−17．如图，△ABC中，AB=AC，D为AC的中点，△ABD的周长比△BDC的周长大2，且BC的边长是方程的2k+14k=1解，求△ABC三边的长．318．如图，AD是△ABC的中线，BE是△ABD的中线．（1）在△BED中作BD边上的高．（2）若△ABC的面积为20，BD=5，则点E到BC边的距离为多少？19．已知△ABC中，AE平分∠BAC（1）如图1，若AD⊥BC于点D，∠B=72°，∠C=36°，求∠DAE的度数；（2）如图2，P为AE上一个动点（P不与A、E重合，PF⊥BC于点F，若∠B＞∠C，则∠EPF=∠B−∠C是否2成立，并说明理由．参考答案1．A2．B3．D4．C5．B6．C7．A8．C9．2a−2b10．2011．112．613．x＝6或x≥1014．解：①当甲、乙、学校三者在同一直线上时若甲、乙在学校的两侧，则甲、乙相距最远为5 km；若甲、乙在学校的同侧，则甲、乙相距最近为3 km.②当甲、乙、学校三者不在同一直线上时甲、乙之间的距离在3～5km之间．15．证明：∵AB=AC=AD∴∠C=∠ABC，∠D=∠ABD∴∠ABC=∠CBD+∠D∵AD∥BC∴∠CBD=∠D∴∠ABC=∠D+∠D=2∠D又∵∠C=∠ABC∴∠C=2∠D．16．解：∵∠A=40°，∠B=72°，∴∠ACB=180°﹣（∠A+∠B），=180°﹣（30°+62°），=180°﹣92°，=88°，∵CE平分∠ACB，∴∠ECB=1∠ACB=44°，∵CD⊥AB于D，∴∠CDB=90°，∴∠BCD=90°﹣∠B=90°2﹣62°=28°，∴∠ECD=∠ECB﹣∠BCD=44°﹣28°=16°，∵DF⊥CE于F，∴∠CFD=90°，∴∠CDF=90°﹣∠ECD=90°﹣16°=74°．17．解：解方程得k=4.5∴BC=4.5∵D为AC中点∴AD=CD∵ΔABD的周长比ΔBDC的周长大2，∴AB+AD+BD−(BC+CD+BD)=2即AB−BC=2∴AB=6.5∵AB=AC∴AC=6.5ΔABC的三边长为6.5,6.5,4.5 18．（1）解：如图所示：（2）解：∵AD是△ABC的中线S△ABC∴S△ABD= 12∵BE是△ABD的中线S△ABD∴S△BED= 12∵△ABC的面积为20∴△EBD的面积是20÷4=5•DB•EH=5∴12∴1×5•EH=52EH=2．即点E到BC边的距离为2．19．证明：（1）如图1，∵∠B=72°，∠C=36°∴∠A=180°﹣∠B﹣∠C=72°；又∵AE平分∠BAC∴∠1=∠A2=72°∴∠3=∠1+∠C=72°又∵AD⊥BC于D∴∠2=90°∴∠DAE=180°﹣∠2﹣∠3=18°．（2）成立．如图2，∵AE平分∠BAC∴∠1=∠BAC2=180°−∠B−∠C2=90°﹣∠B2-∠C2∴∠3=∠1+∠C=90°﹣∠B2+∠C2又∵PF⊥BC于F∴∠2=90°∴∠EPF=180°﹣∠2﹣∠3=∠B−∠C2．。

人教版八年级数学上册与三角形有关的线段练习题(附答案)

人教版八年级数学上册与三角形有关的线段练习题（附答案）一、单选题1.已知等腰△ABC，AB=AC，点D是BC上一点，若AB=10，BC=12，则△ABD的周长可能是（）A. 15B. 20C. 28D. 362.下列各组中，能够构成三角形的是（）A. 2，3，6B. 2，6，8C. 4，4，10D. 4，5，83.已知一个三角形的两边长分别为8cm和3cm，则此三角形第三边的长可能是（）A. 2cmB. 3cmC. 5cmD. 9cm4.下列长度的三根小木棒能构成三角形的是（）A. 1cm，2 cm，3 cmB. 2 cm，4 cm，6 cmC. 3 cm，4 cm，8 cmD. 6 cm，8 cm，10 cm5.下列图形中,线段AD 是△ABC 的高的是（）A. B. C. D.6.如图，D、E分别是AC、BD的中点，△ABC的面积为12cm2，则△BCE的面积是（）A. 6cm2B. 3cm2C. 4cm2D. 5cm27.三角形的两边长分别为和，则第三边长可能为（）A. B. C. D.8.下列图形中具有稳定性的是（）A. 平行四边形B. 三角形C. 长方形D. 正方形9.若一个三角形的两边长分别是4、9，则这个三角形的第三边的长可能是（）A. 3B. 5C. 8D. 1310.下列各组数可能是一个三角形的边长的是（）A. 1，2，6B. 2，3，4C. 4，4，8D. 5，6，12二、填空题11.已知△ABC的两条边长分别为2和5，则第三边c的取值范围是________.12.三角形的三边长分别为3、7、a，且a为偶数，则这个三角形的周长为________。

13.已知三角形的三边长分别为3，5，x，则化简式子________.14.如图，要使五边形木架不变形，至少要再钉上________根木条.15题15.如图，已知点D是△ABC的边BC的中点，点E是边AC的中点，且△ABC的面积为20 ，则△DEC 的面积是________ .16.如图，是的中线，，，那么的周长比的周长多________ ．17题17.如图，分别是△ABC 的高和角平分线，且，则的度数为________．18.三角形有两条边的长度分别是5和7，则第三边a的取值范围是________．三、计算题19.已知△ABC的三边长分别为3、5、a，化简．20.若a，b，c是△ABC的三边的长，化简|a-b-c|+|b-c-a|+|c+a-b|．四、解答题21.在中，已知，若第三边的长为偶数，求的周长.22.在中，，，并且为偶数，求的周长．答案一、单选题1. C2. D3. D4. D5. B6. B7. C8. B9. C 10. B二、填空题11. 3＜c＜7 12. 6或18 13. 7 14. 2 15. 5 16. 2 17. 20°18. 2＜a＜12三、计算题19. 解：∵△ABC的三边长分别为3、5、a，∴5−3＜a＜3＋5，解得：2＜a＜8，故|a＋1|−|a−8|−2|a−2|＝a＋1−（8−a）−2（a−2）＝a＋1−8＋a−2a＋4＝−3．20. 解：根据三角形的三边关系，两边之和大于第三边，得a-b-c＜0，b-c-a＜0，c+a-b＞0．∴|a-b-c|+|b-c-a|+|c+a-b|=b+c-a+c+a-b+c+a-b=3c+a-b．四、解答题21. 解：在中，，第三边的取值范围是：符合条件的偶数是或，当时，的周长为：；当时，的周长为：.的周长为或.22. 解：在中，根据三角形三边关系得：．又因为为偶数，所以，所以的周长为：．。

人教版八年级上册数学11.1与三角形有关的线段专题练习含答案

与三角形有关的线段一、选择题1、已知三角形的两边分别为4和9，则此三角形的第三边可能是（）A． 4 B．5 C．9 D． 132、下列长度的三根木棒首尾相接，不能做成三角形框架的是( )A．5 cm、7 cm、2 cm B．7 cm、13 cm、10 cmC．5 cm、7 cm、11 cm D．5 cm、10 cm、13 cm3、如图，已知BE，CF分别为△ABC的两条高，BE和CF相交于点H，若∠BAC=50°，则∠BHC 为（）A．115°B．120°C．125°D．130°4、下列长度的三条线段，不能组成三角形的是（）A．2、3、4 B．1、2、3 C．3、4、5 D．4、5、65、若△ABC内一点O到三角形三条边的距离相等，则O为△ABC（）的交点．A．角平分线B．高线C．中线D．边的中垂线6、如图，在△ABC中，BD、BE分别是高和角平分线，点F在CA的延长线上，FH⊥BE交BD于G，交BC于H，下列结论：①∠DBE=∠F；②2∠BEF=∠BAF+∠C；③∠F=（∠BAC﹣∠C）；④∠BGH=∠ABE+∠C其中正确的是（）A．①②③B．①③④C．①②④D．①②③④7、下列各组数可能是一个三角形的边长的是（）A．1，2，4 B．4，5，9 C．4，6，8 D．5，5，118、如图，CD，CE，CF分别是△ABC的高、角平分线、中线，则下列各式中错误的是（）A．AB=2BF B．∠ACE=∠ACB C．AE=BE D．CD⊥BE9、一个三角形中直角的个数最多有（）Ａ．3Ｂ．1Ｃ．2Ｄ．010、下列图形不具有稳定性的是（）11、下列各组中的三条线段能组成三角形的是（）Ａ．3，4，8 Ｂ．5，6，11Ｃ．5，6，10 Ｄ．4，4，812、如图所示，其中三角形的个数是（）Ａ．2个Ｂ．3个Ｃ．4个Ｄ．5个13、下列图形不具有稳定性的是（）A．正方形B．等腰三角形C．直角三角形D．钝角三角形14、如图，AC⊥BC，CD⊥AB，DE⊥BC，分别交BC，AB，BC于点C，D，E，则下列说法中不正确的是（）A．AC是△ABC和△ABE的高B．DE，DC都是△BCD的高C．DE是△DBE和△ABE的高D．AD，CD都是△ACD的高二、填空题15、在△ABC是AB＝5，AC＝3，BC边的中线的取值范围是。

人教版八年级数学上册同步练习题第十一章三角形 11.1与三角形有关的线段

人教版八年级数学上册同步练习题第十一章三角形 11.1与三角形有关的线段一、选择题1．三角形一边上的中线把原三角形一定分成两个 ( )A ．形状相同的三角形B ．面积相等的三角形C ．周长相等的三角形D ．直角三角形2．有四根长度分别为3，4，5，x （x 为正整数）的木棒，从中任取三根，首尾顺次相接都能组成一个三角形则组成的三角形的周长（）A ．最小值是11B ．最小值是12C ．最大值是14D ．最大值是153．已知三角形的两边分别为1和4，第三边长为整数，则该三角形的周长为（）A ．7B ．8C ．9D ．104．已知AD 是△ABC 的边BC 上的中线，AB=12，AC=8，则边BC 及中线AD 的取值范围是（）A ．420210BC AD ＜＜，＜＜B ．420420BC AD ＜＜，＜＜C ．210210BC AD ＜＜，＜＜ D ．210420BC AD ＜＜，＜＜5．下列关于三角形的高线的说法正确的是( )A ．直角三角形只有一条高线B ．钝角三角形的高线都在三角形的外部C ．只有一条高线在三角形内部的三角形一定是钝角三角形D ．钝角三角形的三条高线所在的直线的交点一定在三角形的外部6．已知等腰三角形的两条边长为1（（A ．B ．C ．D ．7．在△ABC 中，AB=6，AC=8，则BC 边上中线AD 的取值范围为（）A ．2＜AD ＜14B ．1＜AD ＜7C ．6＜AD ＜8 D ．12＜AD ＜168．已知一个三角形的两边长分别为3和4（则第三边的长不可能．．．的是（（A ．2B ．3C ．4D ．19．不是利用三角形稳定性的是A ．自行车的三角形车架B ．三角形房架C ．照相机的三角架D ．矩形门框的斜拉条10．已知一个三角形的三条边长均为正整数.若其中仅有一条边长为5，它又不是最短边，则满足条件的三角形有（） A ．4B ．6C ．8D ．10二、填空题11．若三角形的两边长分别为6和7（则第三边a 的取值范围是_____（12．AD 是△ABC 的边BC 上的中线，AB=6，AC=4，则边BC 的取值范围是________，中线AD 的取值范围是________． 13．一个三角形3条边长分别为xcm 、（x+1）cm 、（x+2）cm ，它的周长不超过39cm ，则x 的取值范围是_____． 14．三角形的两边长分别是2和3，若第三边的长是奇数，则第三边的长为_____；若第三边的长是偶数，则三角形的周长为______，15．三角形纸片上有100个点，连同三角形的顶点共103个点，其中任意三点都不共线，现以这些点为顶点作三角形，并把纸片剪成小三角形，则这样的三角形共有_______个，三、解答题16．不等边ABC ∆两条高的长度分别为4和12，若第三条高的长度也是整数，求第三条高的长.17．把一条长为18米的细绳围成一个三角形,其中两边长分别为x 米和4米.(1)求x 的取值范围;(2)若围成的三角形是等腰三角形,求x 的值.18．如图，在（ABC 中(AB ＞BC)，AC ＝2BC ，BC 边上的中线AD 把（ABC 的周长分成60和40两部分，求AC 和AB 的长．19．已知a ，b ，c 分别为△ABC 的三条边，且满足23a b c +=-，26a b c -=-，a b >．（1）求c 的取值范围．（2）若ABC ∆的周长为12，求c 的值．20．已知AD 是△ABC 的高,（BAD=72°,（CAD=21°,求∠BAC 的度数.21．已知三角形三条边分别为a+4（a+5（a+6，求a 的取值范围．22．在△ABC 中，AB=AC ，AC 上的中线BD 把△ABC 的周长分别24和18两部分，求三角形三边的长．23．若△ABC 中两边长之比为2：3，三边都是整数且周长为18cm ，求各边的长【参考答案】1．B 2．D 3．C 4．A 5．D 6．B 7．B8．D 9．C 10．D11．1<a<1312．2＜BC ＜10； 1＜AD ＜513．1＜x≤1214． 3 7或915．20116．第三条高的长为5.17．(1)5<x<9(2)x=7.18．AC=48；AB=28.19．（1）36c <<；（2）5c =．20．93°; 51°21．a（（322．16，16，10和12，12，18．23．各边的长分别为4cm ，6cm ，8cm ．。

人教版八年级上数学11.1 与三角形有关的线段同步练习及答案(含答案)

第11章《三角形》同步练习（§11.1 与三角形有关的线段A）班级学号姓名得分1、填空题：(1)由____________三条线段______所组成的图形叫做三角形．组成三角形的线段叫做______；相邻两边的公共端点叫做______，相邻两边所组成的角叫做______，简称______．(2)如图所示，顶点是A、B、C的三角形，记作______，读作______．其中，顶点A所对的边______还可用______表示；顶点B所对的边______还可用______表示；顶点C 所对的边______还可用______表示．(3)由“连接两点的线中，线段最短”这一性质可以得到三角形的三边有这样的性质______________________________．由它还可推出：三角形两边的差____________．(4)对于△ABC，若a≥b，则a＋b______c同时a－b______c；又可写成______＜c＜______．(5)若一个三角形的两边长分别为4cm和5cm，则第三边x的长度的取值范围是____________，其中x可以取的整数值为____________．2．已知：如图，试回答下列问题：(1)图中有______个三角形，它们分别是______________________________________.(2)以线段AD为公共边的三角形是_________________________________________.(3)线段CE所在的三角形是______，CE边所对的角是________________________．(4)△ABC、△ACD、△ADE这三个三角形的面积之比等于______∶______∶______．3．选择题：(1)下列各组线段能组成一个三角形的是( )．(A)3cm，3cm，6cm (B)2cm，3cm，6cm(C)5cm，8cm，12cm (D)4cm，7cm，11cm(2)现有两根木条，它们的长分别为50cm，35cm，如果要钉一个三角形木架，那么下列四根木条中应选取( )．(A)0.85m长的木条(B)0.15m长的木条(C)1m长的木条(D)0.5m长的木条(3)从长度分别为10cm、20cm、30cm、40cm的四根木条中，任取三根可组成三角形的个数是( )．(A)1个(B)2个(C)3个(D)4个(4)若三角形的两边长分别为3和5，则其周长l的取值范围是( )．(A)6＜l＜15 (B)6＜l＜16(C)11＜l＜13 (D)10＜l＜164.(1)一个等腰三角形的周长为18，若腰长的3倍比底边的2倍多6，求各边长．(2)已知等腰三角形的一边等于8cm，一边等于6cm，求它的周长．(3)一个等腰三角形的周长为30cm，一边长为6cm，求其它两边的长．(4)有两边相等的三角形的周长为12cm，一边与另一边的差是3cm，求三边的长．5．(1)若三角形三条边的长分别是7，10，x，求x的范围．(2)若三边分别为2，x－1，3，求x的范围．(3)若三角形两边长为7和10，求最长边x的范围．(4)等腰三角形腰长为2，求周长l的范围．(5)等腰三角形的腰长是整数，周长是10，求它的各边长．6．已知：如图，△ABC中，AB＝AC，D是AB边上一点．(1)通过度量AB 、CD 、DB 的长度，确定AB 与)(21DB CD 的大小关系.(2)试用你所学的知识来说明这个不等关系是成立的．7．已知：如图，P 是△ABC 内一点．请想一个办法说明AB ＋AC ＞PB ＋PC ．8．如图，D 、E 是△ABC 内的两点，求证：AB ＋AC ＞BD ＋DE ＋EC ．第11章《三角形》同步练习（§11.1 与三角形有关的线段B ）班级学号姓名得分1．填空题：(1)从三角形一个顶点向它的对边画______，以______和______为端点的线段叫做三角形这边上的高．如图，若CD 是△ABC 中AB 边上的高，则∠ADC ______∠BDC ＝______，C 点到对边AB 的距离是______的长．(2)连结三角形的一个顶点和它______的______叫做三角形这边上的中线．如右图，若BE 是△ABC 中AC 边上的中线，则AE ______.______21EC(3)三角形一个角的______与这个角的对边相交，以这个角的______和______为端点的线段叫做三角形的角平分线．一个角的平分线与三角形的角平分线的区别是________________________________ ______________________________________．如图，若AD 是△ABC 的角平分线，则∠BAD ______∠CAD ＝21______或∠BAC ＝2______＝2______．2．已知：△GEF ，分别画出此三角形的高GH ，中线EM ，角平分线FN ．3．(1)分别画出△ABC 的三条高AD 、BE 、CF ．(∠A为锐角) (∠A为直角) (∠A为钝角)(2)这三条高AD、BE、CF所在的直线有怎样的位置关系?4．(1)分别画出△ABC的三条中线AD、BE、CF．(2)这三条中线AD、BE、CF有怎样的位置关系?(3)设中线AD与BE相交于M点，分别量一量线段BM和ME、线段AM和MD的长，从中你能发现什么结论?5．(1)分别画出△ABC的三条角平分线AD、BE、CF.(2)这三条角平分线AD、BE、CF有怎样的位置关系?(3)设△ABC的角平分线BE、CF交于N点，请量一量点N到△ABC三边的距离，从中你能发现什么结论?6．已知：△ABC中，AB＝AC，BD是AC边上的中线，如果D点把三角形ABC的周长分为12cm和15cm两部分，求此三角形各边的长．7．(1)如果将一个三角形的三边的长确定，那么这个三角形的形状和大小就不会改变了，三角形的这个性质叫做________________________. (2)四边形是否具有这种性质? 8．将一个三角形剖分成若干个面积相等的小三角形，称为该三角形的等积三角形的剖分(以下两问要求各画三个示意图)(1)已知一个任意三角形，并其剖分成3个等积的三角形． (2)已知一个任意三角形，将其剖分成4个等积的三角形．9．不等边△ABC 的两条高长度分别为4和12，若第三条高的长也是整数，试求它的长．参考答案（§11.1 与三角形有关的线段A ）1．(1)不在同一直线上的，首尾顺次相接，三角形的边，三角形的顶点，三角形的内角，三角形的角．(2)△ABC ，三角形ABC ，BC ，a ；AC ，b ；AB ，c (3)三角形两边之和大于第三边，小于第三边． (4)＞，＜，a －b ，a ＋b(5)1cm ＜x ＜9cm ，2cm 、3cm 、4cm 、5cm 、6cm 、7cm 、8cm ． 2．(1)六，△ABC 、△ABD 、△ABE 、△ACD 、△ACE 、△ADE ． (2)△ABD 、△ACD 、△ADE ． (3)△ACE ，∠CAE ． (4)BC ：CD ：DE ．3．(1)C ，(2)D ，(3)A ，(4)D4．(1)6，6，6；(2)20cm ，22cm ；(3)12cm ，12cm ；(4)5cm ，5cm ，2cm ． 5．(1)3＜x ＜17；(2)2＜x ＜6；(3)10≤x ＜17；(4)4＜e ＜8； (5)3，3，4或4，4，2 6．(1))(21DB CD AB +>． (2)提示：对于△ADC ，∵AD ＋AC ＞DC ， ∴(AD ＋DB )＋AC ＞CD ＋DB ，即AB ＋AC ＞CD ＋DB ．又∵AB ＝AC ，∴2AB ＞CD ＋DB ．从而AB ＞21(CD ＋DB )． 7．提示：延长BP 交AC 于D ．∵在△ABD 中，AB ＋AD ＞BD ＝BP ＋PD ，① 在△DPC 中，DP ＋DC ＞PC ，② 由①、②，∴AB ＋(AD ＋DC )＋DP ＞BP ＋PC ＋DP ．即AB ＋AC ＞PB ＋PC ．8．证明：延长BP 交AC 于D ，延长CE 交BD 于F ．在△ABD 中，AB ＋AD ＞BD ． ① 在△FDC 中，FD ＋DC ＞FC ． ② 在△PEF 中，PF ＋FE ＞PE ． ③①＋②＋③得AB ＋AD ＋FD ＋DC ＋PF ＋FE ＞BD ＋FC ＋PE ，即：AB ＋AC ＋PF ＋FD ＋FE ＞BP ＋PF ＋FD ＋FE ＋EC ＋PE ，所以AB ＋AC ＞BP ＋PE ＋EC ．（§11.1 与三角形有关的线段B ）1．(1)垂线，顶点、垂足，＝，90°，高CD 的长． (2)所对的边的中点、线段，＝，AC(3)平分线，顶点、交点，一个角的平分线是射线，而三角形的角平分线是线段．＝，∠BAC ，∠BAD ，∠DAC 2．略．3．(1)略，(2)三条高所在直线交于一点．4．(1)略，(2)三条中线交于一点，(3)BM ＝2ME ．5．(1)略，(2)三条角平分线交于一点，(3)点N 到△ABC 三边的距离相等． 6．提示：有两种情况，分别运用方程思想，设未知数求解．⎩⎨⎧===,11,8BC AC AB 或⎩⎨⎧===.7,10BC AC AB 7．(1)三角形的稳定性，(2)不具有稳定性．8．(1)(2)下列各图是答案的一部分：9．它的长为5，或4．提示：设S △ABC ＝S ，第三条高为h ，则△ABC 的三边长可表示为：hSS S 212242、、，列不等式得：12242212242SS h S S S +<<- ∴3＜h ＜6．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

《与三角形有关的线段》习题精选1
一、选择题：
1．已知三条线段的比是：①1：3：4；②1：2：3；③1：4：6；④3：3：6；⑤6：6：10；⑥3：4：5．其中可构成三角形的有( )
A．1个B．2个 C．3
个D．4个
2．如果三角形的两边长分别为3和5，则周长L的取值范围是( )
A．6<L<15 B．6<L<16 C．11<L<13 D．10<L<16 3．现有两根木棒，它们的长度分别为20cm和30cm，若不改变木棒的长度，要钉成一个三角形木架，应在下列四根木棒中选取 ( )
A．10cm的木棒 B．20cm的木棒
C．50cm的木棒D．60cm的木棒
4．已知等腰三角形的两边长分别为3和6，则它的周长为( )
A．9 B．12 C．15-
D．12或15
5．已知三角形的三边长为连续整数，且周长为12cm，则它的最短边长为( )
A． 2cm B． 3cm C． 4cm-
D． 5cm
6．已知三角形的周长为9，且三边长都是整数，则满足条件的三角形共有( ) A．2个 B．3个C．4个-
D．5个
二、填空题：
1．若三角形的两边长分别是2和7，则第三边长c的取值范围是________；当周长为奇数时，第三边长为________；当周长是5的倍数时，第三边长为________．2．若等腰三角形的两边长分别为3和7，则它的周长为_______；若等腰三角形的两边长分别是3和4，则它的周长为_____．
3．若等腰三角形的腰长为6，则它的底边长a的取值范围是________；若等腰三角形的底边长为4，则它的腰长b的取值范围是_______．
4．若五条线段的长分别是1cm，2cm，3cm，4cm，5cm，则以其中三条线段为边可构成______个三角形．
5．已知等腰三角形ABC中，AB=AC=10cm，D为AC边上一点，且BD=AD，△BCD的周长为15cm，则底边BC的长为__________．
6．已知等腰三角形的两边长分别为4cm和7cm，且它的周长大于16cm，则第三边长为_____．
三、基础训练：
1．如图所示，已知P是△ABC内一点，试说明PA+PB+PC>1
2
(AB+BC+AC)．
2．已知等腰三角形的两边长分别为4，9，求它的周长．
四、提高训练：
设△ABC的三边a，b，c的长度都是自然数，且a≤b≤c，a+b+c=13，则以a，b，c为边的三角形共有几个？
五、探索发现：
若三角形的各边长均为正整数，且最长边为9，则这样的三角形的个数是多少？
六、中考题与竞赛题：
1．(南京)有下列长度的三条线段，能组成三角形的是( )
A． 1cm， 2cm， 3cm B． 1cm， 2cm， 4cm；
C． 2cm， 3cm， 4cm D． 2cm， 3cm， 6cm
2．(青海)两根木棒的长分别是8cm，10cm，要选择第三根木棒将它们钉成三角形，那么第三根木棒的长x的取值范围是________；如果以5cm为等腰三角形的一边，另一边为10cm，则它的周长为________．
参考答案
一、1．B 2．D 3．B 4．C 5．B 6．B
二、1．5<c<9 6或8 6
2．17 10或11
3．0<a<12 b>2
4．3
5．5cm
6．7cm
三、
1．解：在△APB中，AP+BP>AB，
同理BP+PC>BC，PC+AP>AC，
三式相加得2(AP+BP+PC)>AB+AC+BC，
∴AP+BP+CP>1
2
(AB+AC+BC)．
2．22
四、5个
五、25个
六、1． C
2． 2cm<x< 18cm 25cm．。

人教版-数学-八年级上册-《与三角形有关的线段》习题精选1

8年级数学人教版上册同步练习11.1与三角形有关的线段(含答案解析)

人教版八年级上册(新)数学第11章《11.1与三角形有关的线段》同步习题

八年级数学上册《第十一章与三角形有关的线段》同步练习题及答案-人教版

最新人教版八年级数学上册《与三角形有关的线段1》同步练习及答案.docx

人教版八年级上册数学：11.1 与三角形有关的线段练习卷

人教版数学八年级上册11.1与三角形有关的线段练习 (含答案)

人教版八年级上册 111 与三角形有关的线段同步练习及答案

人教版八年级数学上册第十一章《与三角形有关的线段》课时练习题(含答案)

八年级数学上册第十一章三角形 11.1 与三角形有关的线段习题 (新版)新人教版

人教版八年级数学上册与三角形有关的线段专题训练试题(精品测试卷)

八年级数学上册《第十一章与三角形有关的线段》同步练习题及答案(人教版)

人教版八年级数学上册与三角形有关的线段练习题(附答案)

人教版八年级上册数学11.1与三角形有关的线段专题练习含答案

人教版八年级数学上册同步练习题第十一章三角形 11.1与三角形有关的线段

最新人教版八年级数学上册全册课时练习(一课一练,精选配套习题,附解析)

人教版八年级上数学11.1 与三角形有关的线段同步练习及答案(含答案)

人教版-数学-八年级上册-《与三角形有关的线段》习题精选1

8年级数学人教版上册同步练习11.1与三角形有关的线段(含答案解析)

人教版八年级上册(新)数学第11章《11.1与三角形有关的线段》同步习题

八年级数学上册《第十一章与三角形有关的线段》同步练习题及答案-人教版

最新人教版八年级数学上册《与三角形有关的线段1》同步练习及答案.docx

人教版八年级上册数学：11.1 与三角形有关的线段 练习卷

人教版数学 八年级上册11.1与三角形有关的线段 练习 (含答案)

人教版八年级上册 111 与三角形有关的线段同步练习及答案

人教版八年级数学上册第十一章《与三角形有关的线段》课时练习题(含答案)

八年级数学上册 第十一章 三角形 11.1 与三角形有关的线段习题 (新版)新人教版

人教版八年级数学上册 与三角形有关的线段 专题训练试题(精品测试卷)

八年级数学上册《第十一章与三角形有关的线段》同步练习题及答案(人教版)

人教版八年级数学上册与三角形有关的线段练习题(附答案)

人教版八年级上册数学11.1与三角形有关的线段专题练习含答案

人教版八年级数学上册同步练习题 第十一章三角形 11.1与三角形有关的线段

最新人教版八年级数学上册全册课时练习(一课一练,精选配套习题,附解析)

人教版八年级上数学11.1 与三角形有关的线段 同步练习及答案(含答案)

人教版八年级上册数学：11.1 与三角形有关的线段练习卷

人教版数学八年级上册11.1与三角形有关的线段练习 (含答案)

八年级数学上册第十一章三角形 11.1 与三角形有关的线段习题 (新版)新人教版

人教版八年级数学上册与三角形有关的线段专题训练试题(精品测试卷)

人教版八年级数学上册同步练习题第十一章三角形 11.1与三角形有关的线段

人教版八年级上数学11.1 与三角形有关的线段同步练习及答案(含答案)