直线与圆锥曲线的位置关系(总结归纳)PPT课件
合集下载
直线与圆锥曲线的位置关系精品课件

4 5k 2 x 2 10k (3k 2) x 5(3k 2) 80 0 设M x1 , y1 , N x2 , y 2
则x1 x2 6 k 5
10k 3k 2 6 2 4 5k
直线MN的方程为:x 5 y 28 0 6
2
y2
2
2 px2
OA OB
2 2 2 2
y1 y2 4 p
y1 y2 4 p x1 x2 4 p y1 y2
2
x1 x2 y1 y2 0
x1 x2 y1 y2 4 p
2
(法二):设OA的方程为:y kx y kx 2p 2p A( 2 , ) 2 k k y 2 px
AB
4 2 4 2
2
2
8
(法二) :由上得弦AB的方程为:x y 1 0
运用公式: 1 k 2 x1 x2 1 k 2 AB 而x1 x2 6 x1 x2 1
x1 x2 2 4 x1 x2
AB 8
(法三)(利用抛物线的定义解题)
通常利用方程根与系数的关系求得 应用公式: AB 1 k 2 x1 x2 有关弦中点的问题可利用中点公式及根与系数的 关系解决。 例3、抛物线 y 4 x 的一条弦的中点为 求此弦所在的直线方程。
2
3,2 ,
(法一):设弦交抛物线于A( x1 , y1 ), B( x2 , y2 )
欢迎进入数学多媒体课堂
直线与圆锥曲线的位置关系
一、要点
1、直线与圆锥曲线有无公共点的问题。 2、直线与圆锥曲线相交所得的弦长的计算, 有关中点弦的问题。 3、圆锥曲线内其它涉及到弦的问题。
第十章 第4讲 直线与圆锥曲线的位置关系.pptx

(2)设直线l的方程为y=x+m,A(x1,y1),B(x2,y2),AB的中点为D(x0,y0).
y=x+m, 由1x22 +y42=1,消去
y
整理得
4x2+6mx+3m2-12=0,
由Δ=36m2-16(3m2-12)>0得m2<16,
11
知识衍化体验
考点聚焦突破
则 x0=x1+2 x2=-34m,y0=x0+m=14m,即 D-34m,14m.
所以直线 AB 的斜率为 k=ba22,
设直线方程为 y=ba22(x-3),
13
知识衍化体验
考点聚焦突破
联立直线与椭圆的方程得 (a2+b2)x2-6b2x+9b2-a4=0,
所以 x1+x2=a26+b2b2=2,
又因为a2-b2=9,解得b2=9,a2=18.
答案 1x82 +y92=1
14
18
@《创新设计》
知识衍化体验
考点聚焦突破
∴AP= 23+22+432=435,
又∵原点
O
到直线
l
的距离
d=
2, 5
45 ∴AQ=2 4-45=855,∴AAQP=835=56.
5 法二 由xx= 2+22yy-2=2,4 得 3y2-4y=0,∴yP=43,
由xx= 2+2yy2-=24,,得 5y2-8y=0,∴yQ=85,∴AAQP=43×58=56.
21
知识衍化体验
@《创新设计》 考点聚焦突破
@《创新设计》
【例 2-2】 (2019·南京学情调研)如图,在平面直角坐标系 xOy 中,椭圆 C:ax22+by22= 1(a>b>0)的离心率为 23.且过点1, 23.过椭圆 C 的左顶点 A 作直线交椭圆 C 于另一 点 P,交直线 l:x=m(m>a)于点 M.已知点 B(1,0),直线 PB 交 l 于点 N.
y=x+m, 由1x22 +y42=1,消去
y
整理得
4x2+6mx+3m2-12=0,
由Δ=36m2-16(3m2-12)>0得m2<16,
11
知识衍化体验
考点聚焦突破
则 x0=x1+2 x2=-34m,y0=x0+m=14m,即 D-34m,14m.
所以直线 AB 的斜率为 k=ba22,
设直线方程为 y=ba22(x-3),
13
知识衍化体验
考点聚焦突破
联立直线与椭圆的方程得 (a2+b2)x2-6b2x+9b2-a4=0,
所以 x1+x2=a26+b2b2=2,
又因为a2-b2=9,解得b2=9,a2=18.
答案 1x82 +y92=1
14
18
@《创新设计》
知识衍化体验
考点聚焦突破
∴AP= 23+22+432=435,
又∵原点
O
到直线
l
的距离
d=
2, 5
45 ∴AQ=2 4-45=855,∴AAQP=835=56.
5 法二 由xx= 2+22yy-2=2,4 得 3y2-4y=0,∴yP=43,
由xx= 2+2yy2-=24,,得 5y2-8y=0,∴yQ=85,∴AAQP=43×58=56.
21
知识衍化体验
@《创新设计》 考点聚焦突破
@《创新设计》
【例 2-2】 (2019·南京学情调研)如图,在平面直角坐标系 xOy 中,椭圆 C:ax22+by22= 1(a>b>0)的离心率为 23.且过点1, 23.过椭圆 C 的左顶点 A 作直线交椭圆 C 于另一 点 P,交直线 l:x=m(m>a)于点 M.已知点 B(1,0),直线 PB 交 l 于点 N.
八节直线与圆锥曲线的位置关系PPT课件

(1)当a≠0时,若① Δ>0 ,则直线l与曲线r相交;若② Δ=0 ,则直线l
与曲线r相切;若③ Δ<0 ,则直线l与曲线r相离.
(2)当a=0时,得到一个一次方程,则直线l与曲线r相交,且只有一个交点,
此时,若r为双曲线,则直线l与双曲线的④ 渐近线 平行;若r为抛物线,
则直线l与抛物线的⑤ 对称轴 平行或重合.
a2 b2
(3)椭圆 x2 + y2 =1(a>b>0)与直线Ax+By+C=0相切的条件是A2a2+B2b2=C2.
a2 b2
教材研读 栏目索引
2.双曲线的切线方程
(1)双曲线
x2 a2
-
y2 b2
=1(a>0,b>0)上一点P(x0,y0)处的切线方程是
x0 x a2
-
y0 y b2
=1.
(2)过双曲线
=1(a>b>0)的一条弦,其中点M的坐标为(x0,y0).运
用点差法求直线AB的斜率,设A(x1,y1),B(x2,y2)(x1≠x2),∵A,B都在椭圆上,
∴
x12 a2
x22
a2
y12 b2
y22 b2
1,两式相减得 x12 x22
a2 1,
+
y12
b2
y22
=0,
∴
( x1
(C)
A.1条 B.2条
C.3条
D.4条
答案 C ①当过点(0,1)的直线的斜率不存在时,方程为x=0,与抛物线y2 =4x仅有一个公共点,符合题意. ②当过点(0,1)的直线的斜率存在时,设为k,此时直线为y=kx+1,由
直线与圆锥曲线的位置关系总结归纳ppt课件
a283Fra bibliotek或k<-
3 3 .(*)
25
设 A、B 两点的坐标是 A(x1,y1),B(x2,y2), 则 x1+x2=-1+369k2,x1·x2=1+279k2.
由于以 AB 为直径的圆过原点,∴x1x2+y1y2=0, 即 x1x2+(kx1+2)(kx2+2)=0.
∴(1+k2)x1x2+2k(x1+x2)+4=0, 即271(+1+9kk22)-17+2k92k2+4=0,解得 k=± 331,满足(*)式.
|AB|= 1+k2|x1-x2|= (1+k2)[(x1+x2)2-4x1x2]
= 1+k12|y1-y2|= (1+k12)[(y1+y2)2-4y1y2].
a
13
1.直线y=kx-k+1与椭圆 x2 y2 1 的位置关系为( A )
(A) 相交 (B) 相切 9 (C)4相离
(D) 不确定
的右焦点为
F,若过点
F
的直线
与双曲线的右支有且只有一个交点,则此直线斜率的取值范围
(
33 )A.(- 3 , 3 )
B.(-
3,
3)C.-
33,
33D.[-
3, 3]
x2 y2
又由双曲线方程12- 4 =1,有双曲线的渐近线方程为
y=±
33x,
∴有- 33≤k≤ 33.
• 答案:C
a
15
• 【例1】 已知直线y=(a+1)x-1与曲线y2=ax恰有一 个公共点,求实数a的值.
1
,
1 2
P A 2)若 P 是椭圆上的动点,求线段 中点 M . 的轨迹方程;
(3)过原点O 的直线交椭圆于点 B , C
3 3 .(*)
25
设 A、B 两点的坐标是 A(x1,y1),B(x2,y2), 则 x1+x2=-1+369k2,x1·x2=1+279k2.
由于以 AB 为直径的圆过原点,∴x1x2+y1y2=0, 即 x1x2+(kx1+2)(kx2+2)=0.
∴(1+k2)x1x2+2k(x1+x2)+4=0, 即271(+1+9kk22)-17+2k92k2+4=0,解得 k=± 331,满足(*)式.
|AB|= 1+k2|x1-x2|= (1+k2)[(x1+x2)2-4x1x2]
= 1+k12|y1-y2|= (1+k12)[(y1+y2)2-4y1y2].
a
13
1.直线y=kx-k+1与椭圆 x2 y2 1 的位置关系为( A )
(A) 相交 (B) 相切 9 (C)4相离
(D) 不确定
的右焦点为
F,若过点
F
的直线
与双曲线的右支有且只有一个交点,则此直线斜率的取值范围
(
33 )A.(- 3 , 3 )
B.(-
3,
3)C.-
33,
33D.[-
3, 3]
x2 y2
又由双曲线方程12- 4 =1,有双曲线的渐近线方程为
y=±
33x,
∴有- 33≤k≤ 33.
• 答案:C
a
15
• 【例1】 已知直线y=(a+1)x-1与曲线y2=ax恰有一 个公共点,求实数a的值.
1
,
1 2
P A 2)若 P 是椭圆上的动点,求线段 中点 M . 的轨迹方程;
(3)过原点O 的直线交椭圆于点 B , C
直线与圆锥曲线的位置关系(第一课时)教学课件(共37张PPT)高中数学北师大版选择性必修第一册

拓展:
(1)直线与椭圆相交,则直线与椭圆必有两个交点,反之亦然;而直线与双 曲线或抛物线相交则包含两种情况:①直线与双曲线或抛物线有两个交点, ②直线与双曲线或抛物线有一个交点,此时直线与双曲线的渐近线平行,与 抛物线的对称轴平行或重合. (2)直线与椭圆相切,则直线与椭圆有唯一公共点(切点),反之亦然;直线 与双曲线或抛物线只有一个交点是直线与双曲线或抛物线相切的必要不充分 条件.
2
x1 x2 k
即
x1
x2
1 k
.设线段
MN
的中点为 P x0,
y0
,则 x0
1 2k
,y0
k
1 2k
9 2
4
.
中点
P
在
y
x2
内, 4
1 2k
2
,解得 k
1 4
或k
1 4
.
7.已知抛物线 C : y2 4x 的焦点为 F,过点 F 且斜率为 2 的直线与抛物线 C 交于 A,B
AF 3 5 两点(点 A 在 x 轴的上方),则 BF ___2________.
2 ;若Δ<0,则k
2 或k 2 .
综上,当 k
2 或 k 2 时,直线l与双曲线C没有公共点;当k
2 时,
直线l与双曲线C相切于一点;当 k 1时,直线l与双曲线C相交于一点;当
2 k 1或 1 k 1或1 k 2 时,直线l与双曲线C有两个公共点.
直线与双曲线的位置关系的判断方法:
1.代数法 将直线方程与双曲线方程联立,方程组的解的组数就是直线与双曲线交点的 个数.联立得方程组,消去x或y中的一个后,得到的形如二次方程的式子中, 要注意x2项或y2项的系数是否为零,否则容易漏解.
《直线与圆锥曲线的位置》课件1 (北师大版必修2).ppt

例1.当k为何值时,直线y=kx+k-2与抛物线 y =4x2有两个公共点? 仅有一个公共点? 无公共点。
解:
得k 2x 2+2(k 2-2k-2)x+(k-2)2 =0 ⊿=-16(k2 -2k-1)
1).当⊿>0时,即 2). 当⊿=0时,即
个公共点。 3).当 或
且k≠0时有两个公共点。
或k=0 时,直线与抛物线有一
16 2 10 )2 4 2 9 3 3 4 5 又∵ 点F2(1,0)到直线BF1的距离d= 5
∴CD= 1 ( 2)2 (
1 4 ∴SΔCDF2= CD.d= 10 9 2
点评:本题使用了弦长公式及点到直线的距离公式来解决问题, 这是一种基本的解题方法。
思考题:若将直线绕F1旋转,求⊿CDF2面积的最大值。
直线与圆锥曲线的位置关系
一. 基本方法: 1. 直线与圆锥曲线的位置关系可以通过对直线方 程与圆锥曲线方程组成的二元二次方程组的解的 情况的讨论来研究。即方程消元后得到一个一元 二次方程,利用判别式⊿来讨论(注⊿≠0时,未 必只有二个交点)。 2. 直线与圆锥曲线的位置关系,还可以利用数形 结合、以形助数的方法来解并决。 3. 如果直线的斜率为k,被圆锥曲线截得弦AB两 端点坐标分别为(x1,y1)、(x2,y2)则弦长公式为:
点,|AB|=4 ,则这样的直线存在( ) A.一条 B.二条 C.三条 D.四条
解:观察演示可得三条。选C
四.总结:
1. 利用基本方法,如对方程组解的讨论、弦长公式等是解决问题的基本方法。 2. 数形结合、以形助数是我们解决问题的一个重要思想。
例4.过点(0,2)的直线l与抛物线 y =4x2仅有一个公共点,则
【高中数学课件】直线和圆锥曲线的位置关系1 ppt课件
略解:(向量法)
设 M (x1,y1)N ,(x2,y2) AM (x1,y11 ) AN (x2,y21 ) AM A N AM AN 0
即 x 1 x 2 : y 1 y 2 y 1 y 2 1 0
3b 2 3 2b b 2 3k 2 1 0 b 1 3k 2
1 3k 2 1 3k 2 1 3k 2
你能求出AM的范围吗?
方法1 写出AM的关系式,然后试图值求域。
方法2 考虑以 A(0,1)为圆心, AM 为半径的圆
体现:转化思想 数形结合的思想
(0,-1)
拓展延伸:
对于椭圆x2 a2
y2 b2
1(ab0)的下顶点为A(0,b),
是否存在以A为直角顶点的内接等腰直角三角形AMN?
若存在,这样的三角形可能有几个?叙述并证明你的
能否找到一条斜 k的率直为线 l与此椭圆交于两个不同 的点M,N.使得MA NA,其中A(0,1)?若存在,试 求出k的范围;若不存说 在明 ,理 请由。
想一想:要求变量的范围,如何根据条件建立不等式呢? 让直线方程 联与 立y后 椭 ,得 圆 消到 x 方 的关 程 二于 次 令 0
体现:函数与方程的思想
2
3 k22 b 1 代2 入 b 2 b 得 10
b1(舍 )或 b1 k0 2
解: 由题意得:M,N必在y轴两侧
设 AN 斜率 k(k为 0)则 , AM 的斜率 1 为- k
由 x y 2 k 3 y 2 x 1 3 得 x 2 : 3 (k x 1 )2 3 x N 1 6 3 k k 2 A N 1 k2xN1 3 k21 6 3 k k2 以 1 k代入 k , 上 A 得 = M 式 1 + : 3 k2 的 k2 6 3
直线与圆锥曲线的位置关系 教学课件(共51张PPT) 高中数学人教B版(2019)选择性必修第一册
3
A.
B.2
C.4
D.6
2
解析:由题意得抛物线的焦点为 F(1,0) ,准线方程为 x 1 ,由| BF | 3 及抛物 2
线的定义知点
B
的横坐标为
1 2
,代入抛物线方程得
B
1 2
,
2
.
根据抛物线的对称性,不妨取
B
1 2
,
2
,则直线
l
的方程为
y
2
2 3
(
x
2)
.
联立
y
2
2 3
(x
2),
例 3 判断直线 : = + 1 与双曲线 : 2 − 2 = 1 是否有公共点. 如果有, 求出公共点的坐标.
解:联立直线与双曲线的方程,可得方程组
= +1, 2 − 2 = 1,
消去 ,可得 2 − ( + 1 )2 = 1 ,由此可解得 =− 1. 此时, = 0 .
因此直线与双曲线有一个公共点,且公共点的坐标为 (-1,0) .
y1 , B x2, y2
,则
x12
x22
y12 3 y22 3
1, 两式相减得直线
1,
l
的斜率为
y1 y2 3 x1 x2 3 2 6 .又直线 l 过点 P(2,1) ,所以直线 l 的方程为
x1 x2
y1 y2
1
y 1 6(x 2) ,即 6x y 11 0 ,经检验直线 l 与双曲线有两个交点.故选 A.
得
A(8,
4
y2 4x,
2) ,于是 | AM | 4 .故选 C. | BM |
6.不过原点的直线 l :
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.直线y=kx-k+1与椭圆 x2 y2 1 的位置关系为( A )
(A) 相交 (B) 相切 9 (C)4相离
(D) 不确定
2.已知双曲线方程x2-y2=1,过P(0,1)点的直线l与双曲线
只有一个公共点,则l的条数为( A )
(A)4
(B)3
(C)2
(D)1
3.过点(0,1)与抛物线y2=2px(p>0)只有一个公共点的直线
焦点弦:若弦过圆锥曲线的焦点叫焦点弦;
通径:若焦点弦垂直于焦点所在的圆锥曲线的对称轴, 此时焦点弦也叫通径。=
3.设直线 Ax+By+C=0 与圆锥曲线 f(x,y)=0 相交于 A(x1, y1),B(x2,y2),则弦长
|AB|= 1+k2|x1-x2|= (1+k2)[(x1+x2)2-4x1x2] = 1+k12|y1-y2|= (1+k12)[(y1+y2)2-4y1y2].
y=±
33x,
∴有- 33≤k≤ 33.
• 答案:C
• 【例1】 已知直线y=(a+1)x-1与曲线y2=ax恰有一 个公共点,求实数a的值.
解• 析分证:联结析立论:方程.先组用yy2==代(aax+数. 1)方x-法1,即联(1)立当 a方=0程时,组此解方程决组恰,有再一组从解几为何xy==上10.,验
条数是( D )
(A)0
(B)1
(C)2
y
(D)3
y
0
x
x 0
x2 y2
(2009·福建)已知双曲线12- 4 =1
的右焦点为
F,若过点
F
的直线
与双曲线的右支有且只有一个交点,则此直线斜率的取值范围
(
33 )A.(- 3 , 3 )
B.(-
3,
3)C.-
33,
33D.[-
3, 3]
x2 y2
又由双曲线方程12- 4 =1,有双曲线的渐近线方程为
Y
O
X
种类:相离;相切; 相交(0个交点,一个交点,一个交点或两个交点)
位置关系与交点个数
Y
相交:两个交点
相切:一个交点
O
X 相离:0个交点
Y
O
X
若直线与渐近线平行, 则相交且只有一个交点.
判断直线与双曲线位置关系的操作程序 把直线方程代入双曲线方程
得到一元一次方程
直线与双曲线的 渐进线平行
相交(一个交点)
两式相减可得yx11--yx22·yx11++yx22=-ba22,即 kAB=-ba22xy00
.
x2 y2 类似的可得圆锥曲线为双曲线a2-b2=1
时,有
kAB=ab22yx00.
2px0
圆锥曲线为抛物线 y2=2px(p>0)时,有 kAB= y0 .
求椭圆
x2 9
y2 4
1 被点
Q(2,1)平分的弦 AB
yy
y
y
oo FF xx
o
Fx
o
Fx
3.直线与抛物线的位置关系:
设直线与抛物线方程分别为: y=kx+m与y2=2px:
(1)若直线与对称轴平行或重合,则相交且只有一个交点.
(2)若直线与对称轴相交, 由
y=kx+m y2=2px 得: Ax2+Bx+C=0
故①△>0 相交 ②△=0 相切 ③△<0 相离
a
为
4 0,-1,-5时,
直线 y=(a+1)x-1 与曲线 y2=ax 恰有一个公共点.
三、弦的中点问题
x2 y2 设 A(x1,y1),B(x2,y2)是椭圆a2+b2=1 上不同的两点,
且 x1≠x2,x1+x2≠0,M(x0,y0)为 AB 的中点,则xaxa212222++ybyb212222==11,.
1.直线与椭圆的位置关系:
设直线与椭圆方程分别为:
联立方程组
y=kx+m b2x2+a2y2=a2b2
y=kx+m与 消去y得:
x2 y2 a2 b2 1:
Ax2+Bx+C=0
(1)△>0 相交 (2)△=0 相切 (3)△<0 相离
直线与圆锥曲线的位置关系
2.直线与双曲线的位置关系:
设直线与双曲线方程分别为:
2
x
L4相切
x2
直线L绕着点(0,3)旋转过程中,直线L与双曲线
y2
1
43
的 交点情况如何?L的斜率变化情况如何?
L4 L3 y L2 L1 3
-2
2
x
直线L绕着点(-1,3)转过程中,直线L与抛物线 y 2 4 x
的交 点情况如何?L的斜率变化情况如何?
L
3
y
L2
L1
x
直线与圆锥曲线的位置关系
(2)当 a≠0 时,消去 x,得a+a 1y2-y-1=0.
①若a+a 1=0,即 a=-1,方程变为一元一次方程-y-1=0,
方程组恰有一组解yx==--11.,
a+1 ②若 a ≠0,即
a≠-1,令Δ=0,
得 1+4(a+a 1)=0,可解得 a=-45,这时直线与曲线相切,只有一个公共点.
综上所述知,当
所以“直线与抛物线或双曲线有一个 公共点是直线与抛物线或双曲线相切 的必要不充分条件”
把直线方程代入圆锥曲线方程
得到一元一次方程
双曲线, 直线与 渐近线平行
相交1
抛物线, 直线与 对称轴平行 或重合
相交1
得到一元二次方程 计算判别式
>0 =0 <0
相交 相切 相离
21ຫໍສະໝຸດ 02. 弦:直线被圆锥曲线截得的线段称为圆锥曲线的弦。
y=kx+m与
x2 a2
y2 b2
1:
(1)若直线与渐近线平行, 则相交且只有一个交点.
(2)若直线与渐近线重合, 则相离即没有交点.
(3)若直线与渐近线相交,联立方程组
y=kx+m b2x2-a2y2=a2b2
消去y得: Ax2+Bx+C=0
故①△>0 相交 ②△=0 相切 ③△<0 相离
直线与双曲线位置关系种类
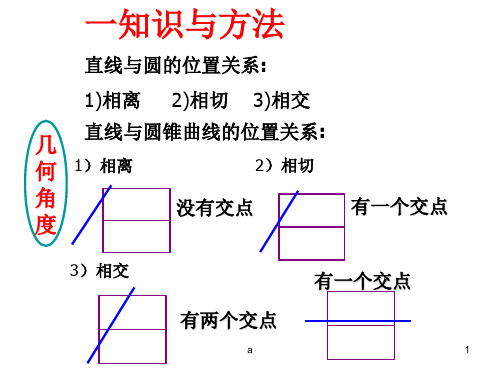
一知识与方法
直线与圆的位置关系:
1)相离 2)相切 3)相交
几 直线与圆锥曲线的位置关系:
何 1)相离
2)相切
角
没有交点
度
有一个交点
3)相交
有两个交点
有一个交点
直线l绕着点(0,3)旋转过程中,与椭圆x 2 y 2 1
43
的交点情况如何?L的斜率变化情况如何?
yl
3 -2 3
L2相切 L3相交
得到一元二次方程 计算判别式
>0 =0 <0 相交 相切 相离
3.直线与抛物线的位置关系:
设直线与抛物线方程分别为: y=kx+m与y2=2px:
(1)若直线与对称轴平行或重合,则相交且只有一个交点.
(2)若直线与对称轴相交, 由
y=kx+m y2=2px 得: Ax2+Bx+C=0
故①△>0 相交 ②△=0 相切 ③△<0 相离
所在的直线方程
.
已知在平面直角坐标系 中的一个椭圆,它的中心在原点,
左焦点为 F ( 3, 0) ,右顶点为 D ( 2, 0 ) ,设点 A
