初中数学教师基本能力竞赛(含答案)
初中数学青年教师基本功大赛笔试试卷(含答案)
A B
5. (本小题 12 分) 从甲地到乙地有 A1、A2 两条路线，从乙地到丙地有 B1、B2、B3 三条路 线，从丙地到丁地有 C1、C2 两条路线．一个人任意先了一条从甲地到丁地的路线．求 他恰好选到 B2 路线的概率是多少？
22ຫໍສະໝຸດ 要 t 最小，即 CT+TQ 最小，而 CT+TQ 是点 C 到直线 C
′B 的折线长，只有当 CT+TQ 成为点 C 到直线 C′B 的
y C
OK
T
x
B
Q H
垂线段时才最小，故作 CH⊥BC′交 OB 于点 K，则点
C′
K 就是使运动时间最短的点。
∵△CBC′为正三角形，∴∠C′CH=30°∴OK=OC·tan30°=2
P138—139） 5. (本小题 12 分)
A1
甲
乙
A2
如图：从甲到丁有 2×3×2=12 种走
9
A
M
B1
C1
B2
丙
C2
丁
B3
N
D
C
B
E
法，而经过线路
B2
共有
2×1×2=4
种走法，故
P=
4 12
1 3
6. (本 小 题 12 分 ) 如 图 ： 裁 剪 线 AB 与 CD 长 恰 好 为 三 棱 柱 底 面 周 长 30cm， 故
BM AB 2 AM 2 30 2 182 24
由△CEB∽△AMB 可知： CB BE ，故 CB 60
AB BM
30 24
初中数学教师基本能力竞赛(含答案)
第5题图第6题初中数学教师基本能力竞赛全卷共四大题28小题，满分150分，考试时间120分钟．一、选择题（本大题共10小题，每小题3分，满分30分）1、雄风商城春节期间，开设一种摸奖游戏，中一等奖的机会为20万分之一，用科学记数法表示为（ ）A 、2×10-5B 、5×10-6C 、5×10-5D 、2×10-62、图(1)表示一个时钟的钟面垂直固定于水平桌面上，其中分针上有一点A ，且当钟面显示3点30分时，分针垂直于桌面，A 点距桌面的高度为10厘米。
如图(2)，若此钟面显示3点45分时，A 点距桌面的高度为16厘米，则钟面显示3点50分时，A 点距桌面的高度为（ ）？A 、（22－3 3）厘米B 、（16＋π）厘米C 、18厘米D 、19厘米3、已知一组正数12345,,,,x x x x x 的方差为：222222123451(20)5S x x x x x =++++-，则关于数据123452,2,2,2,2x x x x x + + + + +的说法：①方差为S 2；②平均数为2；③平均数为4；④方差为4S 2。
其中正确的说法是（ ）A 、 ①②B 、①③C 、②④D 、③④4．如图，ABC ∆的角,,A B C 所对边分别为,,a b c ，点是O ABC ∆的外心，，于，于E AC OE D BC OD ⊥⊥，于F AB OF ⊥ 则OD OE OF =∶∶（ ） ．A 、a b c ∶∶B 、cb a 1:1:1 C 、C B A cos :cos :cos D 、C B A sin :sin :sin5、用三种边长相等的正多边形地砖铺地，其顶点拼在一起，刚好能完全铺满地面．已知正AB CEFO第8题图AB Q Oxy第10题多边形的边数为x 、y 、z ，则zy x 111++的值为（ ） A 、1 B 、32 C 、21 D 、31 6、如图，以Rt △ABC 的斜边BC 为一边在△ABC 的同侧作正方形BCEF ，设正方形的中心为O ，连结AO ，如果AB =4，AO =26，那么AC 的长等于( ) A 、12 B 、16 C 、43 D 、827、已知函数()()()()22113513x x y x x ⎧--⎪=⎨--⎪⎩≤＞，则使y =k 成立的x 值恰好有三个，则k 的值为（ ）A 、0B 、1C 、2D 、38、二次函数2y ax bx c =++的图象如图所示，)2,(n Q 是图象上的一点，且BQ AQ ⊥，则a 的值为（ ）． A 、13- B 、12-C 、－1D 、－2 9、将一枚六个面编号分别为1，2，3，4，5，6的质地均匀的正方体骰子先后投掷两次，记第一次掷出的点数为ａ，第二次掷出的点数为ｂ，则使关于y x ,的方程组223=+=+y x by ax 只有正数解的概率为（ ）A 、121 B 、92 C 、185 D 、3613 10、如图，在平面直角坐标系xoy 中，等腰梯形ABCD 的顶点坐标分别为A （1，1），B （2，-1），C （-2，-1），D （-1，1）。
初中数学青年教师基本功大赛笔试试卷
初中数学青年教师基本功大赛笔试试卷题目一：选择题（共20题，每题2分，共40分）1. 设x=2，y=3，则表达式3x+2y的值为（）。
A. 12B. 13C. 14D. 152. 已知矩形的长为5 cm，宽为3 cm，则该矩形的面积是（）。
A. 8 cm²B. 13 cm²C. 15 cm²D. 18 cm²3. 下列选项中，是2的倍数的数是（）。
A. 9B. 15C. 20D. 254. 简化下列代数式：4x - (3x - 2)的结果是（）。
A. x + 2B. x - 1C. x - 2D. x + 15. 若甲乘以乙的结果是18，而甲除以乙的结果是6，那么甲和乙分别是（）。
A. 15、3B. 9、2C. 12、2D. 6、16. 若一辆汽车以每小时60公里的速度行驶，那么它行驶1小时30分钟可走的距离是（）。
A. 45公里B. 60公里C. 75公里D. 90公里7. 已知等腰直角三角形斜边的长度为5 cm，则该三角形的底边长度是（）。
A. 3 cmB. 4 cmC. 5 cmD. 6 cm8. 小明的体重是45千克，增加了15%，则他的体重变为（）。
A. 50.25千克B. 52千克C. 51.75千克D. 48.75千克9. 若5x−3=12，y+7=15，则x的值是（）。
A. 3B. 4C. 6D. 910. 已知正方形的面积是64 cm²，则该正方形的边长是（）。
A. 4 cmB. 6 cmC. 8 cmD. 16 cm11. 若一辆自行车的速度为每小时20公里，行驶了4小时，则它行驶的总路程为（）。
A. 40公里B. 60公里C. 80公里D. 100公里12. 两个角互为互补角，若其中一个角的度数是45°，则另一个角的度数是（）。
A. 45°B. 60°C. 75°D. 90°13. 小明有一笔钱，他把其中的3/5存入银行，剩下的40元放在家里。
2024年教师资格考试初中学科知识与教学能力数学试卷与参考答案
2024年教师资格考试初中数学学科知识与教学能力复习试卷(答案在后面)一、单项选择题（本大题有8小题，每小题5分，共40分）1、在下列函数中，属于一次函数的是：A.(f(x)=x2+3x−2)B.(g(x)=2x+4)C.(ℎ(x)=√x+5)+3)D.(j(x)=1x2、下列关于三角形内角和定理的说法正确的是：A. 任何三角形的内角和小于180°B. 等边三角形的内角和等于360°C. 所有三角形的内角和等于180°D. 任何三角形的内角和大于180°3、题干：在平面直角坐标系中，点A的坐标为（3，4），点B的坐标为（-2，1）。
下列关于点B的坐标的描述正确的是（）A. 点B在第二象限B. 点B在第三象限C. 点B在第四象限D. 点B在x轴上4、题干：若等差数列{an}的首项为2，公差为3，则第10项an的值为（）A. 25B. 28C. 31D. 345、下列关于函数图像的说法正确的是（）A. 函数y=x^2的图像是一个开口向上的抛物线B. 函数y=√x的图像是一个开口向下的抛物线C. 函数y=2x+1的图像是一条直线，斜率为2，y轴截距为1D. 函数y=|x|的图像是一个开口向左的绝对值函数6、下列关于一元二次方程的解法，错误的是（）A. 因式分解法可以求解一元二次方程B. 配方法可以求解一元二次方程C. 求根公式法可以求解一元二次方程D. 降次法不能求解一元二次方程7、在下列函数中，属于二次函数的是（）)A.(y=1xB.(y=x2+2x+1)C.(y=√x)D.(y=x3−2x2+x+1)8、已知函数(f(x)=2x2−3x+1)，则函数的对称轴是（）)A.(x=−34)B.(x=34)C.(y=−34)D.(y=34二、简答题（本大题有5小题，每小题7分，共35分）第一题请结合初中数学学科特点，谈谈如何有效运用信息技术进行数学教学？第二题题目：简述在教授初中数学时如何运用直观演示法，并举例说明其在几何教学中的应用。
哈尔滨市初中数学教师基本技能大赛试题答案
哈尔滨市初中数学教师基本技能大赛试题答案一、单项选择题：1、A ；2、B ；3、C ；4、A ；5、D ；6、B ；7、B ；8、C ；9、B ；10、C ；11、C ；12、B 。
二、填空题：13、3.84×105；14、x>5；15、2n(m －2n)(m+2n)；16、17；17、5；18、21元；19、150π；20、略； 21、3n+1；22、23π；23、a>-1；24、6。
三、解答题： 25、（1）△AOP ∽△AMB ··················2分∴AP ·AM=AB ·AO=2R 2···················1分 ∴AP ·AM 为定值·························1分 （2）（略）·····························4分26、解：从箱子中抽取一张卡片，每张卡片的机会均等，有10种结果，放回后再抽，也有10种结果，先后抽取两张卡片，一共有100种不同的结果。
哈市初中数学教师基本功大赛
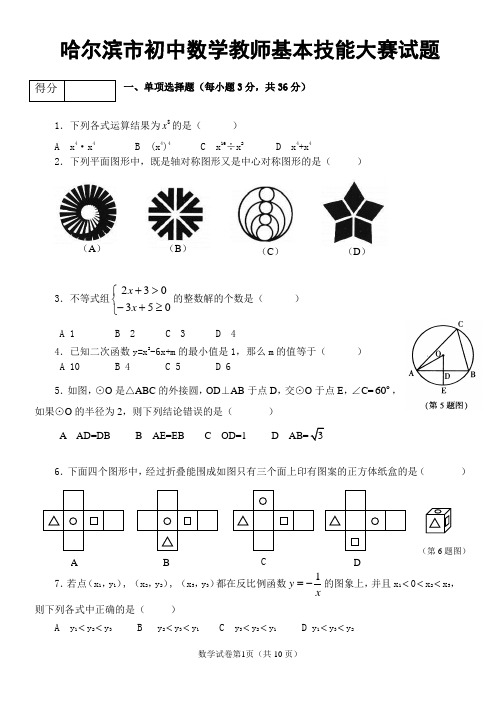
（A ）（B ）（C ）（D ）哈尔滨市初中数学教师基本技能大赛试题一、单项选择题（每小题3分，共36分）1．下列各式运算结果为8x 的是（ ）A x 4·x 4B (x 4)4C x 16÷x 2D x 4+x 42．下列平面图形中，既是轴对称图形又是中心对称图形的是（ ）3．不等式组⎩⎨⎧≥+->+053032x x 的整数解的个数是（ ）A 1B 2C 3D 44．已知二次函数y=x 2-6x+m 的最小值是1，那么m 的值等于（ ） A 10 B 4 C 5 D 65．如图，⊙O 是△ABC 的外接圆，OD ⊥AB 于点D ，交⊙O 于点E ，∠C=60o，如果⊙O 的半径为2，则下列结论错误的是（ ）A AD=DB B AE=EBC OD=1D AB=36．下面四个图形中，经过折叠能围成如图只有三个面上印有图案的正方体纸盒的是（ ） C 7．若点（x 1，y 1）, （x 2，y 2）, （x 3，y 3）都在反比例函数1y x=-的图象上，并且x 1<0<x 2<x 3，则下列各式中正确的是（ ）A y 1<y 2<y 3B y 2<y 3<y 1C y 3<y 2<y 1D y 1<y 3<y 2得分A B D（第6题图）8．只用下列一种正多边形不能镶嵌成平面图案的是（ ） A 正三角形 B 正方形 C 正五边形 D 正六边形 9．如图是关于x 的函数y=kx+b （k ≠0）的图象，则不等式kx+b ≤0的解集在数轴上可表示为（ ）10．如图，将矩形ABCD 沿对角线BD 折叠，使C 落在C ＇处，BC ＇交AD 于点E ，则下列结论不一定成立的是（ ）A AD ＝BC ＇B ∠EBD ＝∠EDBC △ABE ∽△CBD D EDAEABE =∠sin 11．甲、乙二人沿相同的路线由A 到B 匀速行进，A ，B 两地间的路程为20km ．他们行进的路程s （km ）与甲出发后的时间t （h ）之间的函数图像如图所示．根据图像信息，下列说法正确的是（ ）A 甲的速度是4 km/ hB 乙的速度是10 km/ hC 乙比甲晚出发1 hD 甲比乙晚到B 地3 h12．如图，面积为12cm 2的△ABC 沿BC 方向平移至△DEF 的位置，平移的距离是边BC 长的两倍，则图中四边形ACED 的面积为（ ）A 24cm 2B 36cm 2C 48cm 2D 无法确定二、填空题（每小题3分，共36分）13．地球距离月球表面约为384000千米，将这个距离用科学记数法（保留三个有效数字）表示应为__________________千米.14．在函数52-=x x y 中，自变量x 的取值范围是___ __________．15．分解因式:2m 2n －8n 3＝___________________________. 16．当x=-3时，代数式2x 2+3x的值是_____________. 17．如图,在△ABC 中,∠A=30°,tanB=23,AC=32,则AB=________________. 18．某商店把一商品按标价的九折出售（即优惠10%），仍可获利20%，若该商品的标价为每件28元，则该商品的进价为_________元.得分19．一个圆锥形的圣诞帽底面半径为10cm ，母线长为15cm ，则圣诞帽的侧面积为_______cm 2（结 果保留π）.20．已知点P （x ，y ）位于第二象限，并且y ≤x+4，x 、y 为整数，写出一个符合上述条件的点P 的坐标：_______________.21．下面由火柴棒拼出的一列图形中，第n 个图形由n 个正方形组成，根据下图所反映的规律，猜想第n 个图形中火柴棒的根数是___________________（n 是正整数且n ≥1）.22．如图，⊙O 的半径为3，OA=6，AB 切⊙O 于B ，弦BC ∥OA ，连结AC ，图中阴影部分的面积为 ________ ．23．如果a 、b 、c 为互不相等的实数，且满足关系式b 2+c 2=2a 2+16a+14与bc=a 2-4a-5，那么a 的取值范围是_______________．24．如图，△ABC 是边长为3的等边三角形，△BDC 是等腰三角形，且∠BDC ＝120°．以D 为顶点作一个60°角，使其两边分别交AB 于点M ，交AC 于点N ，连接MN ，则△AMN 的周长为 ．三、解答题（其中第25～27题各8分，第28～29题各10分，第30题16分，第31题18分，共78分）25．（本题8分）如图，已知⊙O 的半径为R ，AB 是⊙O 的直径，C 是»AB 的中点，动点M 在»BC 上运动（不与B 、C 重合），AM 交OC 于点P ，OM 与PB 交于点N ．（1）求证：AP ·AM 是定值；（2）请添加一个条件（要求添加的条件是图中两条线段或多条线段之间的数量关系），使OM ⊥PB ．并加以证明．26．（本题8分）在箱子中有10张卡片，分别写有1到10的十个整数，从箱子中任取一张卡片，记下它的读数x ，然后再放回箱子中，第二次再从箱子中任取一张卡片，记下它的读数y ，试求x+y 是10的倍数的概率．得分得分…n=1n=2n=3n=427．（本题8分）请阅读下列材料： 问题：现有5个边长为1的正方形，排列形式如图①，请把它们分割后拼接成一个新的正方形．要 求画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形．小东同学的做法是：设新正方形的边长为x(x ＞0)．依题意，割补前后图形的面积相等，有x 2=5，解得x=5．由此可知新正方形得边长等于两个小正方形组成的矩形对角线的长．于是，画出如图②所示的分割线，拼出如图③所示的新正方形． 请你参考小东同学的做法，解决如下问题： 现有10个边长为1的正方形, 排列形式如图④，请把它们分割后拼接成一个新的正方形．要求：在图④中画出分割线，并在图⑤的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形．说明：直接画出图形，不要求写分析过程．28．（本题满分10分）一服装经销商计划购进某品牌的A 型、B 型、C 型三款服装共60套，每款服装至少要购进8套，且恰好用完购服装款61000元．设购进A 型服装x 套，B 型服装y 套，三款服装的进价和预售价如下表：（1）如果所购进的A 型服装与B 型服装的费用不超过39000元，购进B 型服装与C 型服装的费用不超过34000元，那么购进三款服装各多少套？（2）假设所购进服装全部售出，综合考虑各种因素，该服装经销商在购进这批服装过程中需另外支出各种费用共1500元．①求出预估利润P （元）与x （套）的函数关系式；（注：预估利润P=预售总额 - 购服装款 - 各种费用）②求出预估利润的最大值，并写出此时购进三款服装各多少套．得分得分服装型号 A 型 B 型 C 型 进价（元/套） 900 1200 1100 预售价（元/套） 1200 1600 130029．（本题满分10分）已知：在锐角△ABC中，AB=AC．D为底边BC上一点，E为线段AD上一点，且∠BED=∠BAC=2∠DEC，连接CE．（1）求证：∠ABE=∠DAC；（2）若∠BAC=60°，试判断BD与CD有怎样的数量关系，并证明你的结论；（3）若∠BAC=α那么（2）中的结论是否还成立．若成立，请加以证明；若不成立，请说明理由．30．（本题满分16分）问题：在平面直角坐标系中，直线y＝12x＋5交x轴于点A，交y轴于点B，交直线y＝x－1于点C．过点A作y轴的平行线交直线y＝x－1于点D．点E为线段AD上一点，且tan∠DCE＝12．点P从原点O出发沿OA边向点A匀速移动，同时，点Q从B点出发沿BO边向原点O匀速移动，点P 与点Q同时到达A点和O点，设BQ=m．（1）求点E的坐标；（2）在整个移动过程中，是否存在这样的实数m，使得△PQD为直角三角形．若存在这样的实数m，求m得值，若不存在，请说明理由；（3）函数y＝kx经过点C，R为y＝kx上一点，在整个移动过程中，若以P、Q、E、R为顶点的四边形是平行四边形，求R点的坐标．要求：①解答上面问题；②根据你对上面问题的解答，任意选择其中一问，说出你的主要解题思路．得分得分第30题备用图一31．（本题满分18分）得分习题改编．原题：梯形ABCD，AD∥BC，∠B=900，∠DCB=600，BC=4，AD=2，ΔPMN，PM=MN=NP=a，BC与MN 在一直线上，NC=6，将梯形ABCD向左翻折1800．⑴向左翻折二次，a≥2时，求两图形重叠部分的面积；⑵向左翻折三次，重叠部分的面积等于梯形ABCD的面积，a的值至少应为多少？⑶向左翻折三次，重叠部分的面积恰好等于梯形ABCD的面积的一半，求a的值．。
初中数学青年教师教学基本功比赛试题
初中数学青年教师教学基本功比赛试题一、选择题1. 下列四个分数中，哪一个是一个无限循环小数？A. 0.9B. 0.45C. 0.16D. 0.252. 一个多面体的五个顶点互不相同，它的棱数比它的面数多3，那么这个多面体的面数是多少？A. 5B. 6C. 7D. 83. 下图中，小正方形的边长为1cm。
请问中间的五角星的面积是多少平方厘米？（图片）A. 2B. 2.5C. 34. 已知a:b = 2:3，b:c = 5:6，那么a:c =？A. 5:6B. 3:2C. 4:5D. 1:15. 若5的倒数加上4的倒数等于x的倒数，那么x的值是多少？A. 0.25B. 0.2C. 0.125D. 0.1二、填空题1. 如果a的值为5，b的值为3，那么a的正数次方与b的正数次方的和是多少？答案：1522. 以下列出了一组坐标，请问这些坐标中x轴上的最小值是多少？（6，1），（-3，2），（0，-5），（2，4）答案：-33. 某数的几何平均数是3，算术平均数是4，那么这个数是多少？4. 某个数增加了原来的60%，结果是48，那么这个数原来是多少？答案：305. 在一个等差数列中，首项是2，公差是3，那么这个数列的第11项是多少？答案：32三、解答题1. 一张纸的长度是18cm，宽度是15cm，这张纸的面积是多少平方厘米？2. 请用两种方法计算下列两个分数的和：1/4 + 1/63. 某个数的平方比这个数的三倍大21，求这个数。
4. 一根木棍从一头经过10cm的地方折断，两段的长度分别是3：4，请问原始木棍的长度是多少？5. 下图是一个等边三角形，求阴影部分的面积。
（图片）四、解答题1. 给定函数f(x) = 3x + 1，求f(4)和f(10)的值。
2. 某地一天的气温变化如下：上午9时，气温是18℃，到中午12时气温上升到30℃，下午的最高温度是35℃。
上述变化可以用什么样的图象来表示？3. 请找出以下等差数列中的规律，并给出下一个数：8，14，20，26，32，...4. 甲、乙两人一起筹集某项物资，甲筹集了总数的1/3，乙筹集了总数的2/5，剩下的部分由其他人筹集。
初中数学青年教师教学基本功比赛试题
初中数学青年教师教学基本功比赛试题初中数学青年教师教学基本功比赛试题基础知识测试题（南京下关）一、填空题（共6 小题，每空0.5 分，计10 分）1．数学是研究_____________________ 的科学，这一观点是由__________ 首先提出的．2．通过义务教育阶段的学习，学生能获得适应社会生活和进一步发展所必须的数学的_______ 、 ___________ 、 __________ 、___________ ．3．维果斯基的“最近发展区理论”认为学生的发展有两种水平：一种是学生的__________ 发展水平；另一种是学生______________ 发展水平，两者之间的差异就是最近发展区．4．从数学史上看，有理数的概念传入我国存在着翻译上的错误，其原意是_____________ 数，包括________ 小数和_____________ 小数，_____________ 的发现，引发了第一次数学危机．5．_______ 是概率论发展史上首先被人们研究的概率模型，它具有两个特征：一是_______ 、二是_____________ ．6．波利亚在其名著《怎样解题》中提出的解数学题的四个步骤是：____ ；他认为“怎样解题表”有两个特点，即普遍性和性．二、简答题（共3小题，每小题5分，计15分）7．大约在公元前6 世纪至4世纪之间，古希腊人遇到了令他们百思不得其解的三大尺规作图问题，这就是著名的古代几何学作图三大难题．请你简述这三大难题分别是什么？8．《义务教育数学课程标准》（2011年版）从知识与技能等四个方面对总目标进行了阐述．（1）请写出其他三个方面目标的名称；（2）请简述总目标的这四个方面之间的关系．9．“角平分线上的一点到角的两边距离相等”这一结论在苏教版义务教育数学教材八上的《1.4 线段、角的轴对称性》以及九上的《1.2 直角三角形全等的判定》中都有所出现．请你结合教学实际，简述课本上八上和九上分别是如何引导学生得到这一结论的，说说它们之间的区别、联系和这样安排的意义．参考答案：1．数量关系和空间形式．2．基础知识、基本技能、基本思想、基本活动经验．3．现有，可能的．4．成比例的数，有限，无限循环，无理数．5．古典概型，（试验结果的）有限性，（每个结果的）等可能性．6．弄清问题、拟定计划、实施计划、回顾反思；常识．7．三等分角问题：将任一个给定的角三等分．立方倍积问题：求作一个正方体的棱长，使这个正方体的体积是已知正方体体积的二倍．化圆为方问题：求作一个正方形，使它的面积和已知圆的面积相等．8．（1）数学思考、问题解决、情感态度；（2）四个方面是一个有机的整体；教学要兼顾这四个目标，这些目标的实现，是学生受到良好数学教育的标志；后三个目标的发展离不开知识技能的学习，知识技能的学习必须有利于其他三个目标的实现．9．八上《1.4 线段、角的轴对称性》中是通过学生动手操作，采取折纸的方法折出角的平分线，再过角平分线上一点折出角的两边垂线段，然后度量这两条线段的长度得出结论的；九上《1.2 直角三角形全等的判定》是通过严格的推理论证，采用自己画图、写已知、求证并证明得出结论的．它们的区别是，一个是通过动手操作，一个是通过严格证明．联系是，前面的学习为后面的学习作铺垫，在进行严格的证明之前，学生已经熟练地掌握了这一结论的运用．意义是，符合学生的认知发展规律，使学生的认知从感性上升到理性，既培养了学生的动手能力，又培养了学生的推理论证能力．符带说明：1．专业技能比赛包括基础知识测试和解题能力测试两部分．基础知识测试内容包括数学文化（数学史）常识和数学教育基础知识（教材、课程标准、教育学、心理学、教学论、教学法等）．解题能力测试内容包括基础题（教材中的基本定理、公式的证明，教材例题、习题、复习题）与综合题（与中考中档题难度相当）．2．第1、2、8 题考查对《课标》学习和理解情况（称为课标板块）；第4、5、7 题结合苏教版初中数学教科书的教学内容对数学史进行简单的考查（称为数学史板块）；第3、6、9 题是对心理学、数学教育学、教材和教学法等相关知识的考查（称为综合板块）．2012 年雨花台区小学数学青年教师教学基本功比赛教育教学知识常识比赛试卷（满分 100分，时间 60 分钟）姓名 成绩一、填空题：本大题共 8个小题，共 22个空，每空 1分，共 22分。
初中数学教师基本能力竞赛(含答案)
第5题图第6题初中数学教师基本能力竞赛全卷共四大题28小题，满分150分，考试时间120分钟．一、选择题（本大题共10小题，每小题3分，满分30分）1、雄风商城春节期间，开设一种摸奖游戏，中一等奖的机会为20万分之一，用科学记数法表示为（ ）A 、2×10-5B 、5×10-6C 、5×10-5D 、2×10-62、图(1)表示一个时钟的钟面垂直固定于水平桌面上，其中分针上有一点A ，且当钟面显示3点30分时，分针垂直于桌面，A 点距桌面的高度为10厘米。
如图(2)，若此钟面显示3点45分时，A 点距桌面的高度为16厘米，则钟面显示3点50分时，A 点距桌面的高度为（ ）？A 、（22－3 3）厘米B 、（16＋π）厘米C 、18厘米D 、19厘米3、已知一组正数12345,,,,x x x x x 的方差为：222222123451(20)5S x x x x x =++++-，则关于数据123452,2,2,2,2x x x x x + + + + +的说法：①方差为S 2；②平均数为2；③平均数为4；④方差为4S 2。
其中正确的说法是（ ）A 、 ①②B 、①③C 、②④D 、③④4．如图，ABC ∆的角,,A B C 所对边分别为,,a b c ，点是O ABC ∆的外心，，于，于E AC OE D BC OD ⊥⊥，于F AB OF ⊥ 则OD OE OF =∶∶（ ） ．A 、a b c ∶∶B 、cb a 1:1:1 C 、C B A cos :cos :cos D 、C B A sin :sin :sin5、用三种边长相等的正多边形地砖铺地，其顶点拼在一起，刚好能完全铺满地面．已知正AB CEFO第8题图AB QOxy 第10题多边形的边数为x 、y 、z ，则zy x 111++的值为（ ） A 、1 B 、32 C 、21 D 、31 6、如图，以Rt △ABC 的斜边BC 为一边在△ABC 的同侧作正方形BCEF ，设正方形的中心为O ，连结AO ，如果AB =4，AO =26，那么AC 的长等于( ) A 、12 B 、16 C 、43 D 、827、已知函数()()()()22113513x x y x x ⎧--⎪=⎨--⎪⎩≤＞，则使y =k 成立的x 值恰好有三个，则k 的值为（ ）A 、0B 、1C 、2D 、38、二次函数2y ax bx c =++的图象如图所示，)2,(n Q 是图象上的一点，且BQ AQ ⊥，则a 的值为（ ）． A 、13- B 、12-C 、－1D 、－2 9、将一枚六个面编号分别为1，2，3，4，5，6的质地均匀的正方体骰子先后投掷两次，记第一次掷出的点数为ａ，第二次掷出的点数为ｂ，则使关于y x ,的方程组223=+=+y x by ax 只有正数解的概率为（ ）A 、121 B 、92 C 、185 D 、3613 10、如图，在平面直角坐标系xoy 中，等腰梯形ABCD 的顶点坐标分别为A （1，1），B （2，-1），C （-2，-1），D （-1，1）。
教师基本功比赛----=常州市武进区初中数学教师解题竞赛试题及参考答案
武进区初中数学教师解题竞赛试题命题人：于新华一、选择题（每题6分）1、如果一个三角形的一条边是另一条边的2倍，并且有一个角是30°，那么这个三角形的形状是 （ ）A 、直角三角形B 、钝角三角形C 、锐角三角形D 、不能唯一确定2、如图，正比例函数)0(＞k kx y =与反比例函数xy 1=的图象相交于A 、C 两点，过A 作x 轴的垂线交x 轴于B ，连结BC ，若△ABC 的面积为S ，则 （ ）A 、S ＝1B 、S ＝2C 、S ＝3D 、S 的值不确定3、某工厂第二季度比第一季度的产值增长了x ％，第三季度的产值又比第二季度的产值增长了x ％。
则第三季度的产值比第一季度的产值增长了 （ ）A 、2x ％B 、1＋2 x ％C 、（1＋x ％）x ％D 、（2＋x ％）x ％4、设P ＝121220022001++，Q ＝121220032002++，则P 与Q 的大小关系是 （ ）A 、P ＞QB 、P ＝QC 、P ＜QD 、不能确定5、边长为整数，周长等于21的等腰三角形共有 （ ） A 、4个 B 、5个 C 、6个 D 、7个6、如果1x 、2x 是两个不相等的实数，且满足12003121=-x x ，12003222=-x x ，那么21x x 等于 （ ）A 、2003B 、－2003C 、1D 、－17、若实数x ，y 满足条件06222=+-y x x ，则x y x 222++的最大值是 （ ）A 、14B 、15C 、16D 、不能确定 8、如图1，图中平行四边形共有的个数是 （ ） A 、40 B 、38 C 、36 D 、30AB CDPABCD（图1） （图2） （图3）9、如图2，矩形ABCD 被分割成六个正方形，其中最小正方形的面积等于1，则矩形ABCD 的面积等于 （ ）A 、152B 、143C 、132D 、10810、如图3，若PA ＝PB ，∠APB ＝2∠ACB ，AC 与PB 交于点D ，且PB ＝4，PD ＝3，则AD ·DC 等于 （ ）A 、6B 、7C 、12D 、16二、填空题（每题6分）11、△ABC 中，AB ＝32，AC ＝2，BC 边上的高为3，则BC 边的长为＿＿＿＿。
数学教师教学基本功比赛测试卷(一)初级中学教师基本功大赛试题附答案
初级中学数学教师教学基本功比赛测试卷（一）一、新课程标准，填空。
（每空2分，共20分）1数学是人们对客观世界定性把握和 、逐渐 、形成方法和理论，并进行广泛应用的过程。
2 教师的主要任务是激发学生的 ，向学生提供充分从事数学活动的机会，帮助学生成为学习的 。
3、初中阶段的数学内容分为数与代数、 、统计与概率和 四个领域。
4、动手操作、 、 是学生学习数学的重要方式。
5、不同的人在数学上得到不同的发展的意思是：教学要面向全体，必须适应每一位学生的 ；人的发展不可能整齐划一，必须 ，尊重差异。
二、专业知识（共70分）（一）填空题（每小题2分，共8分）1、如图，己知⊙O 的半径为5，弦AB=8，P 是弦AB 上的任意一点，则OP 的取值范围是 。
2、已知关于x 的不等式组⎩⎨⎧--0x 230a x ＞＞的整数解共有6个，则a 的取值范围是 。
3、若ABC ∆的三边a 、b 、c 满足条件：222338102426a b c a b c +++=++，则这个三角形最长边上的高为 。
4、抛物线()2226y x =--的顶点为C ，已知3y kx =-+的图象经过点C ，则这个一次函数图象与两坐标轴所围成的三角形面积为 。
（二）选择题（每小题3分，共12分）5．如图，由几个小正方体组成的立体图形的左视图是6．有5张写有数字的卡片（如图1），它们的背面都相同，现将它们背面朝上（如图2），从中翻开任意一张是数字2的概率是（ ）OPBA羽毛球 25% 体操40%A ．15 B ．25C ．23D ．127．正方形网格中，AOB ∠如图放置，则tan ∠AOB 的值为（ ）Ａ．55Ｂ．55Ｃ．12Ｄ．28. 已知甲、乙两组数据的平均数都是5，甲组数据的方差2112S =甲，乙组数据的方差2110S =乙，则以下说法正确的是（ ） Ａ．甲组数据比乙组数据的波动大Ｂ．乙组数据比甲组数据的波动大 Ｃ．甲组数据与乙组数据的波动一样大Ｄ．甲、乙两组数据的波动大小不能比较（三）解答题（共50分） 9．(本题满分6分)01112tan 30()3231---；10．(本题满分6分)因式分解：a 2x 2－4+a 2y 2－2a 2xy ；11．(本题满分6分)某学校为了学生的身体健康，每天开展体育活动一小时，开设排球、篮球、羽毛球、体操课．学生可根据自己的爱好任选其中一项，老师根据学生报名情况进行了统计，并绘制了下边尚未完成的扇形统计图和频数分布直方图，请你结合图中的信息，解答下列问题：ABO（1）该校学生报名总人数有多少人？（2）选羽毛球的学生有多少人？选排球和篮球的人数分别占报名总人数的百分之几？ （3）将两个统计图补充完整 12．（本题满分10分） 如图，点A ，B ，C ，D 是直径为AB 的⊙O 上四个点，C 是劣弧BD 的中点，AC 交BD 于点E ， AE ＝2， EC ＝1．（1）求证：DEC △∽ADC △；（2）连结DO ，试探究四边形OBCD 是否是菱形？若是，请你给予证明并求出它的面积；若不是，请说明理由．（3）延长AB 到H ，使BH ＝OB ，求证：CH 是⊙O 的切线．13，（本题满分10分）某污水处理公司为学校建一座三级污水处理池，平面图形为矩形，面积为200平方米（平面图如图22所示的ABCD ）.已知池的外围墙建造单价为每米400元.中间两条隔墙建造单价每米300元，池底建造的单价为每平方米80元（池墙的厚度不考虑）（1）如果矩形水池恰好被隔墙分成三个正方形，试计算此项工程的总造价（精确到100元）（2）如果矩形水池的形状不受（1）中长、宽的限制，问预算45600元总造价，能否完成此项工程？试通过计算说明理由.（3）请给出此项工程的最低造价（多出部分只要不超过100元就有效）.14，（本题满分12分）已知抛物线C 1：y ＝－x 2+2mx +n （m ，n 为常数，且m ≠0，n ＞0）的顶点为A ，与y 轴交于点C ，抛物线C 2与抛物线C 1关于y 轴对称，其顶点为B ，连结AC 、BC 、AB .（1）写出抛物线C 2的解析式；（2）当m ＝1时，判定△ABC 的形状，并说明理由；（3）抛物线C 1是否存在点P ，使得四边形ABCP 为菱形？如果存在，请求出m 的值；如果不存在，请说明理由.A D 隔 隔 墙 墙BC 图22答案一、新课标（20分）1、定量刻画、抽象概括2学习积极性、主人3空间与图形、课题学习4自主探究、合作交流5发展需要、承认差异二、专业知识（共70分）（一）填空题（共8分）1、3≤OP≤52、－5≤a＜－43、60134、1（二）选择题（共12分））5、 A6、 B7、 D8、B （三）解答题（共70分）9.原式=332(32233(31)(31)+⨯--+……..……….2分331)2-………………4分3312-=-3 ………………6分10.a2x2－4+a2y2－2a2xy=（a2x2－2a2xy+a2y2）－4 …………………2分= a2（x2－2xy+y2）－4= a2（x-y）2－22 ………………4分=( a x-ay+2）( a x–ay-2）………………6分11．解：（1）设该校报名总人数为x人，则由两个统计图可得40%160x=．∴x=16016040040%0.4==（人）． ·······················································1分（2）设选羽毛球的人数为y,则由两个统计图可得y＝40025%100⨯=（人）． ·····························2分因为选排球的人数是100人，所以10025%400=， ·································3分因为选篮球的人数是40人，所以4010%400=， ·························································································4分即选排球．篮球的人数占报名的总人数分别是25%和10%．（3）如图···························································································6分12．（共10分）（1）证明：∵C 是劣弧BD 的中点，∴ DAC CDB ∠=∠． 而ACD ∠公共，∴ DEC △∽ADC △． ·························· 1分 （2）证明：由⑴得DC ECAC DC=， ∵ 1.213CE AC AE EC ==+=+=， ∴2313DC AC EC ==⨯= ． ∴3DC = ．（2分）由 已知3BC DC ==AB 是⊙O 的直径，∴90ACB ∠=︒． ∴ 222223312AB AC CB =+=+=． ∴23AB =∴ 3OD OB BC DC ====． ∴ 四边形OBCD 是菱形． ········································································· 5分 过C 作CF 垂直AB 于F ，连结OC ，则3OB BC OC ===． ∴ 60OBC ∠=︒． ∴ sin 60CFBC︒=，33sin 60322CF BC =︒==， ∴ 33332BCD S OB CF =⨯==菱形O ． ··················································· 7分 （3）证明：连结OC 交BD 于G ，∵ 四边形OBCD 是菱形， ∴OC BD ⊥且OG GC =．又 已知OB ＝BH ，∴ BG CH ∥． ∴90OCH OGB ∠=∠=︒，∴CH 是⊙O 的切线． ·································································· 10分13，（共10分）（1）设AB＝x，则AD＝3x，依题意3x2＝200，x≈8.165.设总造价W元.W＝8x×400+2x×300+200×80＝3800x+16000＝47000（元）.（2）设AB＝x，则AD＝200 x.所以(2x+200x×2)×400+2x×300+80×200＝45600.整理，得7x2－148x+800＝0.此时求根公式中的被开方式＝－496＜0，所以此方程无实数解，即预算45600元不能完成此项工程.（3）估算：造价45800元. (2x+400x)×400+600x+16000＝45800.整理，得7x2－149x+800＝0.此时求根公式中的被开方式＝－199＜0，仍不够.造价46000元，同法可得7x2－150x+800＝0.此时求根公式中的被开方式＝100＞0，够了.造价45900元，可得求根公式中的被开方式＝－49.75＜0，不够.最低造价为46000元.14（共12分），（1）y＝－x2－2mx+n.（2）当m＝1时，△ABC为等腰直角三角形.理由如下：因为点A与点B关于y轴对称，点C又在y轴上，AC＝BC，过点A作抛物线C的对称轴交x轴于D.过点C作CE⊥AD于E.当m＝1时，顶点A的坐标为A（1，1+n），CE ＝1，又点C的坐标为（0，n），AE＝1+n－n＝1，所以AE＝CE，∠ECA＝45°，∠ACy＝45°，由对称性知∠BCy＝45°，∠ACB＝90°，所以△ABC为等腰直角三角形.（3）假设抛物线C，上存在点P，使得四边形ABCP为菱形，则PC＝AB＝BC，由（2）知，AC＝BC，AB＝BC＝AC，从而△ABC为等边三角形，所以∠ACy＝∠BCy＝30°.又四边形ABCP为菱形，且点P在C1上，点P与点C关于AD对称，PC与AD的交点也为E，∠ACE ＝90°－30°＝60°，点A、C的坐标分别为A（m，m2+n），C（0，n），AE2＝m2+n－n＝m2，CE＝│m│，在Rt•△ACE中，tan60°＝2||AE mCE m＝3，│m│＝3.所以m＝±3．故抛物线C上存在点P，使得四边形ABCP为菱形.此时m＝±3.。
抚顺市初中数学科教师基本功竞赛选拔试题答案
解得 --------------------------------------------------------------------5分
（ ）---------------------------------------------6分
（2）设日均获利为 元，则
---------------------------9分
当 时， 最大值为200．--------------------------------------------11分
答：当销售单价为7元时，日均获利最多为200元．-----------------12分
13、（本题满分12分）
如图2，当 为底时，过点 作 的平行线，与双曲线在第一象限内的交点为 ．
由于 ，因此 ，从而 ．作 轴， 为垂足，
则 ，设 ，则 ，
由点 ，得点 ，
因此 ．
解之得 （ 舍去），因此点 ．
此时 ，与 的长度不相等，故四边形 是梯形．10分
如图3，当过点 作 的平行线，与双曲线在第三象限内的交点为 时，
同理可得，点 ，四边形 是梯形．12分
综上所述，函数 图象上存在点 ，使得以 四点为顶点的四边形为梯形，点 的坐标为： 或 或 ．14分
FD=FE------------------------------------------------------------------------------------------- 1分
14．解：（1）如表
数据段
频数
频率
10
0.05
初中数学解题能力比赛试题(含答案)
HGDCABEFOD CBA初中数学教师解题能力比赛试题卷一、选择题（本题共7个小题，每小题4分，共28分）请将正确答案填在下表中。
题号 123456 7答案D A C B C AD1．方程x 2﹣2x+﹣4=0的实数解的个数是（ ）A ．0B ．1C ．2D ．32．如图，已知ΔABC 中，AB=5，AC=3，BC 上的中线AD=2，则BC 的长为.A ．132B ．4C ．13D ．23． 已知：四边形ABCD 中，AB =3，CD =4，M 、N 分别是AD ，BC 的中点， 则线段MN 的取值范围是（ ） A ．1＜MN ＜7 B ．1＜MN ≤7 C ．21＜MN ≤27 D ．21＜MN ＜274．二次函数()3-m -x 2-y 2=，x ≥-l 时，y 随x 的增大而减小， 则m 的取值范围是（ ）A ．m = -lB ．m ≤-lC ．m >-lD ．m ≥-l5．如图，已知：点E 、F 分别是正方形ABCD 的边BC AB 、的中点，DF BD 、分别交CE 于点H G 、，若正方形ABCD 的面积是240，则四边形BFHG 的面积等于（ ）A ． 24B ．26C ．28D ．306. 以半圆的一条弦BC （非直径）为对称轴将弧BC 折叠后 与直径AB 交于点D ，若32=DB AD ，且AB=5，则CB =（ ） A ．52 B ．32 C ． 22 D ．27. 2012年11月11日，支付宝24小时交易创历史新高，达191亿元。
某物流公司的快递车和货车同时从甲地出发，以各自的速度匀速向乙地行驶，快递车到达乙地后卸完物品再另装货物共用45分钟，立即按原路以另一速度匀速返回，直至与货车相遇．已知货车的速度为60千米／时，两车之间的距离y (千米)与货车行驶时间x (小时)之间的函数图象如图所示，现有以下4个结论： ①快递车从甲地到乙地的速度为100千米／时；②甲、乙两地之间的距离为300千米；③图中点B 的坐标为(334，75)；④快递车从乙地返回时的速度为90千米／时． 以上4个结论中正确的是（ ）A ．①②③B ．①②④C ．②③④D ．①②③④ABC二、填空题（本题7个小题，每小题4分，共28分）请将正确答案填在下表中。
初中数学教师基本能力竞赛(含问题详解)
第5题图第6题初中数学教师基本能力竞赛全卷共四大题28小题，满分150分，考试时间120分钟．一、选择题（本大题共10小题，每小题3分，满分30分）1、雄风商城春节期间，开设一种摸奖游戏，中一等奖的机会为20万分之一，用科学记数法表示为（ ）A 、2×10-5B 、5×10-6C 、5×10-5D 、2×10-62、图(1)表示一个时钟的钟面垂直固定于水平桌面上，其中分针上有一点A ，且当钟面显示3点30分时，分针垂直于桌面，A 点距桌面的高度为10厘米。
如图(2)，若此钟面显示3点45分时，A 点距桌面的高度为16厘米，则钟面显示3点50分时，A 点距桌面的高度为（ ）？A 、（22－3 3）厘米B 、（16＋π）厘米C 、18厘米D 、19厘米3、已知一组正数12345,,,,x x x x x 的方差为：222222123451(20)5S x x x x x =++++-，则关于数据123452,2,2,2,2x x x x x + + + + +的说法：①方差为S 2；②平均数为2；③平均数为4；④方差为4S 2。
其中正确的说法是（ ）A 、 ①②B 、①③C 、②④D 、③④4．如图，ABC ∆的角,,A B C 所对边分别为,,a b c ，点是O ABC ∆的外心，，于，于E AC OE D BC OD ⊥⊥，于F AB OF ⊥ 则OD OE OF =∶∶（ ） ．A 、a b c ∶∶B 、cb a 1:1:1 C 、C B A cos :cos :cos D 、C B A sin :sin :sin5、用三种边长相等的正多边形地砖铺地，其顶点拼在一起，刚好能完全铺满地面．已知正AB CEFO第8题图多边形的边数为x 、y 、z ，则zy x 111++的值为（ ） A 、1 B 、32 C 、21 D 、31 6、如图，以Rt △ABC 的斜边BC 为一边在△ABC 的同侧作正方形BCEF ，设正方形的中心为O ，连结AO ，如果AB =4，AO =26，那么AC 的长等于( ) A 、12 B 、16 C、 D、7、已知函数()()()()22113513x x y x x ⎧--⎪=⎨--⎪⎩≤＞，则使y =k 成立的x 值恰好有三个，则k 的值为（ ）A 、0B 、1C 、2D 、38、二次函数2y ax bx c =++的图象如图所示，)2,(n Q 是图象上的一点，且BQ AQ ⊥，则a 的值为（ ）． A 、13- B 、12-C 、－1D 、－2 9、将一枚六个面编号分别为1，2，3，4，5，6的质地均匀的正方体骰子先后投掷两次，记第一次掷出的点数为ａ，第二次掷出的点数为ｂ，则使关于y x ,的方程组223=+=+y x by ax 只有正数解的概率为（ ）A 、121 B 、92 C 、185 D 、3613 10、如图，在平面直角坐标系xoy 中，等腰梯形ABCD 的顶点坐标分别为A （1，1），B （2，-1），C （-2，-1），D （-1，1）。
教师解题基本功竞赛(初中数学)及答案
B（第11题图） 21OEF D BA 6．一家医院某天出生了3个婴儿，假设生男生女的机会相同，那么这3个婴儿中，出现2个男婴、1个女婴的概率是7．如图，方格纸中4个小正方形的边长均为1，则图中阴影部分三个小扇形的面积和为 （结果保留π）. 物线232--=x ax y 与x 轴正半轴交于点A （3，0）.以8．如图，抛OA 为边在x 轴上方作正方形OABC ，延长CB 交抛物线于点D ，再以BD 为边向上作正方形BDEF. 则点F 的坐标9．如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为16cm 2，则该半圆的半径为 cm.10．如图，由1个正方形和1个等腰直角三角形拼在一起所组成的图形，把它分成4个全等的图形（在图上分）。
第10题11．如图,四边形OABD 为菱形,点B 、D 在以点O 为圆心的弧EF 上， 若OA = 3， ∠1 =∠2，则扇形OEF 的面积为_________.12．已知二次函数2y ax bx c =++的图象与x 轴交于点(20)-，、1(0)x ，，且112x <<，与y 轴的正半轴的交点在(02)，的下方．下列结论：①420a b c -+=；②0a b <<；③20a c +>；④210a b -+>．其中正确的结论是 （填序号）.二、解答题：（本大题共90分．解答时应写出必要的计算过程、推演步骤或文字说明．） 13．（本题10分）如图，在平面直角坐标系中，直线334y x =-与x 轴、y 轴分别交于A B ，两点．现有半径为1的动圆位于原点处，以每秒1个单位的速度向右作平移运动，则经过多少秒，动圆与直线AB 相切．（第7题）第9题图AAAA14．（本题12分）甲、乙二人同时从A 地出发，沿同一条道路去B 地，途中都使用两种不同的速度1v 与2v (12v v )，甲一半的路程．．使用速度1v 、另一半的路程．．使用速度2v ；乙一半的时间．．使用速度1v 、另一半的时间．．使用速度2v ． (1)甲、乙二人从A 地到达B 地的平均速度各是多少(用1v 和2v 表示)？(2)甲、乙二人谁先到达B 地？为什么？(3) 如图是甲从A 地到达B 地的路程s 与时间t 的函数图像，请你在图中画出相应的乙从A 地到达B 地的路程s 与时间t 的函数图像．15. （本题12分）如图12，Rt △ABC 中，∠C ＝90°，按题目所给条件及要求将相应的直角三角形，分割成若干个全等的并且分别与原三角形相似的三角形．．．．．．．．．．．．．．．．．．．．．．．．．画出图形并简要说明理由．第（1）图AC=BC 将ΔABC 分割成2个三角形；第（2）图AB=2AC 将ΔABC 分割成3个三角形；第（3）图将ΔABC 分割成4个三角形；第（4）图BC=2AC将ΔABC 分割成5个三角形；x16．（本题10分）某公司准备投资开发A 、B 两种新产品，通过市场调研发现：如果单独投资A 种产品，则所获利润（万元）与投资金额x （万元）之间满足正比 例函数关系：A y kx =；如果单独投资B 种产品，则所获利润（万元）与投资金额x （万元）之间满足二次函数关系：2B y ax bx =+．根据公司信息部的报告，A y ，B y （万元）与投资金额x （万元）的部分对应 值如右表所示：⑴填空：A y = ；B y = ；⑵如果公司准备投资20万元同时开发A 、B 两种新产品，设公司所获得的总利润为w （万元），试写出w 与某种产品的投资金额x 之间的函数关系式．⑶请你设计一个在⑵中能获得最大利润的投资方案，并求出按此方案能获得的最大利润是多少万元？ 17．（本题10分）如图，某工厂D 与A ，B 两地有公路、铁路相连，且A C DB E D →→→→与路程相等，2BE CD =，CDE →→的路程为120千米，A C D C D E →→→→比的路程远10千米。
2024年教师资格考试初级中学学科知识与教学能力数学试题及解答参考
2024年教师资格考试初级中学数学学科知识与教学能力复习试题(答案在后面)一、单项选择题（本大题有8小题，每小题5分，共40分）1、已知函数(f(x)=x2−4x+5)，则该函数的最小值是多少？•A) 1•B) 2•C) 3•D) 42、在直角坐标系中，点P(3, -4) 关于原点对称的点Q 的坐标是？•A) (-3, 4)•B) (3, 4)•C) (-3, -4)•D) (3, -4)3、在平面直角坐标系中，点A（2，-3）关于直线y=-x的对称点B的坐标是（）A.（3，2）B.（-3，-2）C.（-2，-3）D.（-3，3）4、下列函数中，函数值y随自变量x增大而减小的是（）A. y=2x+3B. y=-x+5C. y=x^2+1D. y=-3x^25、下列关于三角形的内角和的说法，正确的是（）A、三角形的内角和一定等于180度B、三角形的内角和可能大于180度C、三角形的内角和可能小于180度D、三角形的内角和可以根据三角形形状变化6、对于函数 y = 2^x，当 x > 0 时，关于该函数的性质描述正确的是（）A、y 的值小于 2B、y 的值大于 2C、y 的值随 x 的增大而减小D、y 的值随 x 的增大而增大7、在数学教学中，为了更好地帮助学生理解抽象的数学概念，教师采用的具体教学策略是（）。
A. 多次重复讲解法B. 利用多媒体辅助教学C. 实例教学与比较教学相结合D. 直接抽象教学8、在组织学生进行探究活动时，教师应关注的重点不包括以下几点中的（）。
A. 确保学生安全B. 学生是否遵循了探究步骤C. 探究活动对学生兴趣的激发D. 探究活动是否达到了教学目标二、简答题（本大题有5小题，每小题7分，共35分）第一题请简述数学学科核心素养的主要内容及其在初中数学教学中的体现。
第二题题目：简述基于问题解决的教学模式及其在初中数学教学中的应用，并举例说明。
第三题请简述课堂提问的艺术，并举例说明教师在设计提问时应该注意的几点。
初中数学教师能力检测试卷(附答案)
初中数学教师能力检测试卷(附答案)初中数学教师能力检测试卷（附答案）一、选择题（每题5分，共25分）1. 下列选项中，既是有理数又是无理数的是（）A. 0.333…B. √2C. 3/4D. -π{答案：D}2. 若两个角互为补角，则其中一个角的度数是（）A. 30°B. 45°C. 135°D. 90°{答案：D}3. 已知等差数列的前三项分别为2，5，8，则该数列的第四项是（）A. 11B. 12C. 13D. 14{答案：A}4. 下列函数中，奇函数是（）A. y = x²B. y = |x|C. y = 2xD. y = 3x² - 1{答案：C}5. 若平行四边形ABCD的对角线交于点E，已知BE=4，CE=6，则BD的长度是（）A. 5B. 10C. 12D. 16{答案：B}二、填空题（每题5分，共25分）1. 若一个正方形的边长为a，则其对角线的长度为（）{答案：a√2}2. 已知函数f(x) = 2x + 1，求f(3)的值。
{答案：7}3. 若等差数列的首项为3，公差为2，则第五项的值为（）{答案：13}4. 两个互质的正整数的最小公倍数是它们的（）{答案：乘积}5. 在三角形ABC中，已知∠A=40°，∠B=50°，则∠C的度数为（）{答案：90°}三、解答题（共50分）1. （10分）已知函数f(x) = 2x + 1，求f(x)的值域。
{答案：值域为全体实数。
}2. （15分）解方程组：\[\begin{cases}2x + 3y = 8 \\x - y = 1\end{cases}\]{答案：x=2，y=1}3. （20分）已知等差数列的前三项分别为2，5，8，求该数列的通项公式。
{答案：an=3n-1}4. （5分）证明：任意正整数n，都有n²+1是偶数。
{答案：证明见附录。
初中数学教师基本功竞赛试卷(附答案)
初中数学教师基本功竞赛试卷(附答案)第一题 - 四则运算计算下列各式的结果：1. $12 + 5 =$2. $20 - 8 =$3. $4 \times 7 =$4. $36 \div 9 =$答案：1. $12 + 5 = 17$2. $20 - 8 = 12$3. $4 \times 7 = 28$4. $36 \div 9 = 4$第二题 - 分数计算对下列各题进行分数计算：1. $\frac{3}{4} + \frac{1}{2} =$2. $\frac{5}{8} - \frac{1}{4} =$3. $\frac{2}{3} \times \frac{3}{5} =$4. $\frac{2}{9} \div \frac{1}{3} =$答案：1. $\frac{3}{4} + \frac{1}{2} = \frac{5}{4}$2. $\frac{5}{8} - \frac{1}{4} = \frac{3}{8}$3. $\frac{2}{3} \times \frac{3}{5} = \frac{6}{15}$4. $\frac{2}{9} \div \frac{1}{3} = \frac{6}{9}$第三题 - 方程求解解下列方程：1. $2x + 3 = 9$2. $\frac{3}{4}x - \frac{1}{2} = 1$3. $5 - 2x = 8$4. $\frac{1}{3}x + 5 = 7$答案：1. $x = 3$2. $x = \frac{9}{5}$3. $x = -1.5$4. $x = 6$第四题 - 几何图形选择正确的答案：1. 三角形的内角和为多少？- A. 90度- B. 180度- C. 360度- D. 45度答案：B. 180度2. 一个正方形有几条对角线？- A. 1条- B. 2条- C. 4条- D. 0条答案：C. 4条3. 直线与平行线相交，对应角为：- A. 互补角- B. 对顶角- C. 相等角- D. 余角答案：B. 对顶角4. 直角三角形的斜边是：- A. 最长边- B. 最短边- C. 邻边- D. 对边答案：A. 最长边第五题 - 数学推理根据给定的条件选择正确的答案：1. 如果$a = 3$，$b = 5$，则$a + b =$ _____？- A. 7- B. 8- C. 9- D. 15答案：A. 82. 如果$a = 2$，$b = 4$，则$a \times b =$ _____？- A. 2- B. 4- C. 6- D. 8答案：D. 83. 如果$a = 6$，$b = 2$，则$a - b =$ _____？- A. 2- B. 3- C. 4- D. 5答案：C. 44. 如果$a = 10$，$b = 2$，则$a \div b =$ _____？- A. 1- B. 2- C. 5- D. 10答案：B. 5以上是初中数学教师基本功竞赛试卷及答案。
初中数学教师综合素质竞赛考试卷(90分钟)
初中数学教师综合素质竞赛考试卷（90分钟）一、学习义务教育阶段《数学课程标准（修订版）》的若干核心概念的检测题． （参赛教师从中选择您最熟悉的六个问题作答，每题5分，计30分；以0.3的权重计入总成绩。
）1、数学是研究 数量关系和空间形式 的科学。
2、教学活动是师生积极参与、交往互动、共同发展的过程。
有效的教学活动是学生学与教师教的统一，学生是学习的 主体 ，教师是学生学习的 组织者、引导者 与 合作者 。
3、学生学习应当是一个 生动活泼的、主动的和富有个性的 过程。
除接受式学习外， 动手实践、自主探索 与 合作交流 同样是学习数学的重要方式。
学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程。
4、教师的教学应该以学生的认知发展水平和已有的经验为基础，面向 全体学生 ，注重 启发式 和 因材施教 。
5、学习评价的主要目的是为了全面了解学生数学学习的过程和结果，激励学生学习和改进…教师教学。
应建立 目标多元、方法多样 的评价体系。
6、九年义务教育各学段中，《数学》安排了四个部分的课程内容： “数与代数”， “图形与几何”， “统计与概率”， “综合与实践” 。
7、在数学教学中，应当注重发展学生的数学能力，它包含 数感、符号意识、空间观念、 几何直观、 数据分析观念、 运算能力、 推理能力 和 模型思想 等八个方面的成分。
8、为了适应时代发展对人才培养的需要，义务教育阶段的数学教育要特别注重发展学生的 实践 意识和 创新 意识。
9、通过义务教育阶段的数学学习，学生能获得适应社会生活和进一步发展所必需的数学的 基础知识、 基本技能、 基本思想、 基本活动经验 （简称四基）。
10、数学的课程设计和教学活动组织中，应同时兼顾到 知识技能、 数学思考、 问题解决、 情感态度 四个方面的目标。
这些目标的整体实现，是学生受到良好数学教育的标志，它对学生的全面、持续、和谐发展有着重要的意义。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第5题图第6题初中数学教师基本能力竞赛全卷共四大题28小题，满分150分，考试时间120分钟．一、选择题（本大题共10小题，每小题3分，满分30分）1、雄风商城春节期间，开设一种摸奖游戏，中一等奖的机会为20万分之一，用科学记数法表示为（ ）A 、2×10-5B 、5×10-6C 、5×10-5D 、2×10-62、图(1)表示一个时钟的钟面垂直固定于水平桌面上，其中分针上有一点A ，且当钟面显示3点30分时，分针垂直于桌面，A 点距桌面的高度为10厘米。
如图(2)，若此钟面显示3点45分时，A 点距桌面的高度为16厘米，则钟面显示3点50分时，A 点距桌面的高度为（ ）？A 、（22－3 3）厘米B 、（16＋π）厘米C 、18厘米D 、19厘米3、已知一组正数12345,,,,x x x x x 的方差为：222222123451(20)5S x x x x x =++++-，则关于数据123452,2,2,2,2x x x x x + + + + +的说法：①方差为S 2；②平均数为2；③平均数为4；④方差为4S 2。
其中正确的说法是（ ）A 、 ①②B 、①③C 、②④D 、③④4．如图，ABC ∆的角,,A B C 所对边分别为,,a b c ，点是O ABC ∆的外心，，于，于E AC OE D BC OD ⊥⊥，于F AB OF ⊥ 则OD OE OF =∶∶（ ） ．A 、a b c ∶∶B 、cb a 1:1:1 C 、C B A cos :cos :cos D 、C B A sin :sin :sin5、用三种边长相等的正多边形地砖铺地，其顶点拼在一起，刚好能完全铺满地面．已知正AB CEFO第8题图AB Q Oxy第10题多边形的边数为x 、y 、z ，则zy x 111++的值为（ ） A 、1 B 、32 C 、21 D 、31 6、如图，以Rt △ABC 的斜边BC 为一边在△ABC 的同侧作正方形BCEF ，设正方形的中心为O ，连结AO ，如果AB =4，AO =26，那么AC 的长等于( ) A 、12 B 、16 C 、3 D 、827、已知函数()()()()22113513x x y x x ⎧--⎪=⎨--⎪⎩≤＞，则使y =k 成立的x 值恰好有三个，则k 的值为（ ）A 、0B 、1C 、2D 、38、二次函数2y ax bx c =++的图象如图所示，)2,(n Q 是图象上的一点，且BQ AQ ⊥，则a 的值为（ ）． A 、13-B 、12- C 、－1 D 、－2 9、将一枚六个面编号分别为1，2，3，4，5，6的质地均匀的正方体骰子先后投掷两次，记第一次掷出的点数为ａ，第二次掷出的点数为ｂ，则使关于y x ,的方程组223=+=+y x by ax 只有正数解的概率为（ ）A 、121 B 、92 C 、185 D 、3613 10、如图，在平面直角坐标系xoy 中，等腰梯形ABCD 的顶点坐标分别为A （1，1），B （2，-1），C （-2，-1），D （-1，1）。
y 轴上一点P （0，2）绕点A 旋转180°得点P 1，点P 1绕点B 旋转180°得点P 2，点P 2绕点C 旋转180°得点P 3，点P 3绕点D 旋转180°得点P 4，…，重复操作依次得到点P 1，P 2，…，则点P 2012的坐标是( ) A 、（2012，2） B 、（2012，-2） C 、（2010，0）D 、（-2012，0）二、填空题（本大题共10小题，每小题4分，共40分） 11、已知关于x 的分式方程21212-+=--++x x ax x x x 的解为正数，则a 的范围为 。
12、池塘中竖着一块碑，在高于水面1米的地方观测，测得碑顶的仰角为︒20，测得碑顶在水中倒影的俯角为︒30（研究问题时可把碑顶及其在水中的倒影所在的直线与水平线垂直），则水面到碑顶的高度为 （精确到0.01米，747.270tan ≈︒）。
13、若反比例函数的图像与一次函数xky =b ax y +=的图像相交于),5(),,2(n B m A -两点，则的值等于b a +3 。
14.如图，已知直线1l ∥2l ∥3l ∥4l ∥5l ，相邻两条平行直线间的距离都相等，如果直角梯形ABCD 的三个顶点在平行直线上，90=∠ABC 且AB=3AD ，则αtan = 。
15、如图，点E 是矩形ABCD 的对角线BD 上的一点，且BE =P 为线段EC 延长线上的任意一点，且PQ ⊥BC 于点Q ，PR ⊥BD 于点R 。
则PR 与PQ 之间具有怎样的数量关系式： 。
16、如图，两平行线AB 、CD 间的距离为6，点M 为AB 上一定点。
圆心为O 的扇形纸片MOP 在AB 、CD 之间（包括AB 、CD ），其半径为4，设∠MOP =α。
现将扇形纸片MOP 绕点M 在AB 、CD 之间顺时针旋转，若扇形纸片MOP 旋转过程中，要保证点P 能落在直线CD 上，请确定α的取值范围 。
（参考数据：sin 49°=34，cos 41°=34，tan 37°=34） 17、如图，△ABD 和△ACE 是等腰直角三角形，∠BAD 与∠CAE 是直角，若AB =4，BC =2，AC =3，则DE 的长为 ．18．如图，正方形1112A B PP 的顶点1P 、2P 在反比例函数2(0)y x x=>的图象上，顶点1A 、1B 分别在x 轴、y 轴的正半轴上，再在其右侧作正方形2232B A P P ，顶点3P 在反比例函αA BCD第14题图2l 1345l 第15题第16题(第18题) 1P 2P1A 1B 2A2B3PxyOOADCEOADC 数2(0)y x x=>的图象上，顶点2A 在x 轴的正半轴上，则点3P 的坐标为 。
19、如图, 两圆同心, 半径分别为6与8, 又矩形ABCD 的边AB 和 CD 分别为小大两圆的弦. 则当矩形ABCD 面积最大时, 求此矩形的周长 。
20、已知直线AB 交平面直角坐标系xoy 两坐标轴的A (10，0)、B （0，5）两点，在直线AB上有一动点M ，在坐标系内有另一点N ，若以点O 、B 、M 、N 为顶点构成的四边形为菱形，则点N 的坐标为 。
三、解答题（共8小题，满分80分．解答应写出必要的文字说明、演算步骤或证明过程．）21. 阅读下面材料：小伟遇到这样一个问题，如图1，在梯形ABCD 中，AD ∥BC ，对角线AC ，BD 相交于点O 。
若梯形ABCD 的面积为1，试求以AC ，BD ，AD BC +的长度为三边长的三角形的面积。
小伟是这样思考的：要想解决这个问题，首先应想办法移动这些分散的线段，构造一个三角形，再计算其面积即可。
他先后尝试了翻折，旋转，平移的方法，发现通过平移可以解决这个问题。
他的方法是过点D 作AC 的平行线交BC 的延长线于点E ，得到的△BDE 即是以AC ，BD ，AD BC +的长度为三边长的三角形（如图2）。
参考小伟同学的思考问题的方法，解决下列问题： 如图3，△ABC 的三条中线分别为AD ，BE ，CF 。
（1）在图3中利用图形变换画出并指明以AD ，BE ，CFFE DABC图2第19题第17题的长度为三边长的一个三角形（保留画图痕迹）；（2）若△ABC的面积为1，则以AD，BE，CF的长度为三边长的三角形的面积等于_______。
22、如图1是甲、乙两个圆柱形水槽的轴截面示意图，乙槽中有一圆柱形铁块立放其中（圆柱形铁块的下底面完全落在乙槽底面上）．现将甲槽的水匀速注入乙槽，甲、乙两个水槽中水的深度y（厘米）与注水时间x（分钟）之间的关系如图2所示．根据图象提供的信息，解答下列问题：（1）图2中折线ABC表示________槽中水的深度与注水时间的关系，线段DE表示_______槽中水的深度与注水时间之间的关系（以上两空选填“甲”或“乙”），点B的纵坐标表示的实际意义是________________________________；（2）注水多长时间时，甲、乙两个水槽中水的深度相同？（3）若乙槽底面积为36平方厘米（壁厚不计），求乙槽中铁块的体积；（4）若乙槽中铁块的体积为112立方厘米，求甲槽底面积（壁厚不计）．甲槽乙槽图1AD CBP 1 P 2 P 3 P 4 Q 1Q 2 Q 3 Q 4 图323．某课题研究小组就图形面积问题进行专题研究，他们发现如下结论： （1）有一条边对应相等的两个三角形面积之比等于这条边上的对应高之比； （2）有一个角对应相等的两个三角形面积之比等于夹这个角的两边乘积之比；…现请你继续对下面问题进行探究，探究过程可直接应用上述结论．（S 表示面积） 问题1：如图1，现有一块三角形纸板ABC ，P 1，P 2三等分边AB ，R 1，R 2三等分边AC ． 经探究知2121R R P P S 四边形＝13 S △ABC ，请证明．问题2：若有另一块三角形纸板，可将其与问题1中的拼合成四边形ABCD ，如图2，Q 1，Q 2三等分边DC ．请探究2211P Q Q P S 四边形与S 四边形ABCD 之间的数量关系．问题3：如图3，P 1，P 2，P 3，P 4五等分边AB ，Q 1，Q 2，Q 3，Q 4五等分边DC ．若 S 四边形ABCD ＝1，求3322P Q Q P S 四边形．问题4：如图4，P 1，P 2，P 3四等分边AB ，Q 1，Q 2，Q 3四等分边DC ，P 1Q 1，P 2Q 2，P 3Q 3 将四边形ABCD 分成四个部分，面积分别为S 1，S 2，S 3，S 4．请探究出含有S 1，S 2，S 3，S 4的一个等式．ABC图1P 1 P 2R 2 R 1ABC图2P 1 P 2 R 2 R 1DQ 1Q 2ADP 1 P 2 P 3BQ 1Q 2 Q 3 C 图4S 1 S 2 S 3 S 424、（2011•江苏苏州）已知二次函数()()2680y a x x a =-+>的图象与x 轴分别交于点A 、B ，与y 轴交于点C ．点D 是抛物线的顶点．(1)如图①，连接AC ，将△OAC 沿直线AC 翻折，若点O 的对应点O '恰好落在该抛物线的对称轴上，求实数a 的值；(2)如图②，在正方形EFGH 中，点E 、F 的坐标分别是（4，4）、（4，3），边HG 位于边EF 的右侧．小林同学经过探索后发现了一个正确的命题：“若点P 是边EH 或边HG 上的任意一点，则四条线段PA 、PB 、PC 、PD 不能与任何一个平行四边形的四条边对应相等（即这四条线段不能构成平行四边形）．”若点P 是边EF 或边FG 上的任意一点，刚才的结论是否也成立？请你积极探索，并写出探索过程；(3)如图②，当点P 在抛物线对称轴上时，设点P 的纵坐标t 是大于3的常数，试问：是否存在一个正数a ，使得四条线段PA 、PB 、PC 、PD 与一个平行四边形的四条边对应相等（即这四条线段能构成平行四边形）？请说明理由．25、如图，给出一个基本的几何模型，其中D 、E 分别在△ABC 的边AB 、AC 上，DE ∥BC ，那么我们有一些结论，如：△ADE ∽△ABC ，BCDE AC AE AB AD ==等等.教师如果能设计一些与该模型有密切联系的数学问题要求学生去解决，肯定会较好地激发起学生的求知欲望.请你编写一道数学题目并给出解答，使学生在解决此问题要涉及到 该模型.这里给你两个例子，例1得分较低，例2得分较高.例1、如图DE 平行BC ，AD =2，DB =6，EC 比AE 的2倍还大1，求AC 的长.例2、如图，平行四边形ABCD 对角线交于O ，E 在BC 延长线上，OE 交CD 于F ，AB =3，BC =4，CF =1，求CE 的长.（解题时延长EO 交AB 于G ）.（给出的例子略去了解答，你所编的题目必须给出解答）26、(浙教版八下P 147、3):（原题展示）如图10，分别以△ABC 的边AB 、AC 为一边向外作正方形AEDB 和正方形ACFG ，连结CE 、BG 。