第六章 金属晶体的结构
《高一化学金属晶体》课件

金属键
金属晶体结构多样
由于金属原子半径较大,金属键较弱 ,导致金属晶体具有多种结构,如面 心立方、体心立方、六方密排等。
金属原子之间通过共享电子形成的化 学键。
金属晶体的结构
01
02
03
面心立方结构
金属原子分布在立方体的 八个顶点和六个面心上,方结构
金属原子分布在立方体的 八个顶点和体心位置,形 成次紧密堆积。如钠、钾 等碱金属。
医疗领域
金属在医疗领域的应用主要涉及医疗器械和植入物。例如,不锈钢和钛 合金等金属广泛应用于手术刀具、缝合线、人工关节等医疗器械和植入 物的制造。
PART 05
金属晶体的发展前景
新材料的研发
新材料研发是推动金属晶体发展的关键因素之一。随着科技的不断进步,人们对 于新材料的需求越来越高,这为金属晶体的发展提供了广阔的空间。
金属晶体在受到外力作用时,内部原 子或分子的相对位置发生变化,但仍 保持金属键结合,表现出良好的延展 性。
延展性的影响因素
金属的延展性与金属内部原子或分子 的结合力、金属的种类、温度等因素 有关。
金属的硬度与强度
硬度与强度
硬度是指金属抵抗外力压入的能力,强度是指金属抵抗外力拉伸的能力。
硬度与强度的关系
金属晶体与其他材料的复合应用
金属晶体与其他材料的复合应用是当前研究的热点之一。通 过将金属晶体与其他材料进行复合,可以实现优势互补,提 高材料的综合性能。
复合材料的应用涉及到多个领域,如电子、能源、环保等, 具有广泛的市场前景和应用价值。
2023 WORK SUMMARY
《高一化学金属晶体 》ppt课件
REPORTING
目录
• 金属晶体简介 • 金属晶体的类型 • 金属晶体的性质与结构的关系 • 金属晶体的应用 • 金属晶体的发展前景
金属的晶体结构与结晶PPT课件
3.2 纯金属的结晶
(2)变质处理
变质处理是在浇注前向液态金属中加入一些细 小的难熔的物质(变质剂),在液相中起附加 晶核的作用,使形核率增加,晶粒显著细化。
(3)振动处理
金属结晶时,利用机械振动、超声波振动,电 磁振动等方法,既可使正在生长的枝晶熔断成 碎晶而细化,又可使破碎的枝晶尖端起晶核作 用,以增大形核率。
第27页/共31页
Fe3C的晶体结构
3.5 合金的结晶
➢共晶转变 从一定化学成分的液体合金中同时结晶出两种
不同固相的机械混合物,则该转变过程称为共 晶转变。 ➢共析转变 在固态下由一种单相固溶体同时析出两种不同 固相的机械混合物,则该转变过程称为共析转 变。
第28页/共31页
3.6 金属铸锭的组织结构
内位错线的总长度表示。位 错密度愈大,塑性变形抗力 愈大。因此,目前通过塑性 变形,提高位错密度,是强 化金属的有效途径之一。
第8页/共31页
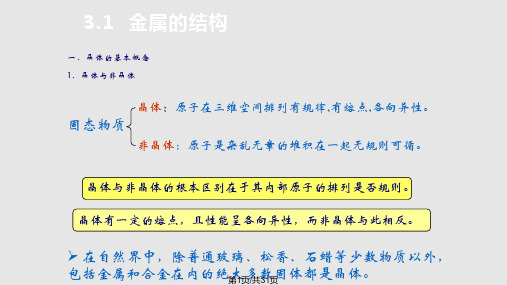
3.1 金属的结构
(3)面缺陷
面缺陷即晶界和亚晶界。
➢晶界:晶粒之间原子无规 则排列的过渡层,又称大 角度晶界。
➢亚晶界:晶粒内部亚组织 之间的边界,一系列刃型 位错所形成的小角度晶界。
晶界和亚晶界处表现出有较高的强度和硬度。 晶粒越细小晶界和亚晶界越多,它对塑性变形的阻碍作用就越大, 金属的强度、硬度越高。
第9页/共31页
3.2 纯金属的结晶
结晶:金属由液态转变为固态晶体的现象叫做结晶。
一、纯金属的冷却曲线和冷却现象
1、冷却曲线
以极缓慢速度冷却
第10页/共31页
实际冷却条件下的冷却
二、柱状晶粒区(垂直于铸锭表面)
化学金属晶体知识点总结

化学金属晶体知识点总结一、金属晶体的基本概念金属晶体是由金属原子以一定规律排列组成的固体结构。
金属晶体具有一些特点,如具有金属典型的电性能、热性能和光学性能,同时还具有良好的延展性、韧性和导电性。
二、金属晶体的结构金属晶体的结构是由金属原子通过化学键相互连接而形成的。
金属晶体的结构有多种类型,其中最常见的是面心立方晶体结构和体心立方晶体结构。
金属晶体的结构对金属的性能具有重要影响,比如面心立方晶体结构使得金属具有优良的导电性和导热性,而体心立方晶体结构使得金属具有良好的韧性和延展性。
三、金属晶体的性能1. 导电性:金属晶体中的自由电子能够在晶体结构中自由传导,因此金属具有良好的导电性能。
2. 导热性:金属晶体中的自由电子能够在晶体结构中迅速传递热量,因此金属具有良好的导热性能。
3. 延展性:金属晶体中的金属原子之间的化学键相对较弱,因此金属具有良好的延展性能,可以被拉伸成细丝或者铺展成薄片。
4. 韧性:金属晶体中的金属原子之间的化学键相对较强,因此金属具有良好的韧性能,可以经受一定的外力而不易断裂。
5. 耐腐蚀性:金属晶体中的化学键特点使得金属具有一定的抗腐蚀性能,可以抵御外界腐蚀物质的侵蚀。
四、金属晶体的制备金属晶体的制备方法有多种,常见的包括熔融法、沉淀法、溶胶-凝胶法等。
熔融法是通过将金属加热至熔点后冷却凝固成固体晶体;沉淀法是通过将金属盐溶液中加入适量还原剂使金属物质析出,然后经过洗涤、干燥等处理制备金属晶体;溶胶-凝胶法是通过将金属盐加入溶液中形成凝胶后再经过热处理的方法制备金属晶体。
五、金属晶体的应用金属晶体广泛应用于工业生产中,主要包括金属材料、金属合金、金属催化剂等。
金属材料广泛用于航空航天、汽车制造、机械加工等领域;金属合金具有优异的物理性能和化学性能,用于制备高强度、高耐热、高耐腐蚀的材料;金属催化剂广泛用于化工生产中的有机合成、空气净化等领域。
总的来说,金属晶体是由金属原子组成的固体结构,在工业生产和科研领域有重要应用。
金属晶体的常见结构

金属晶体的常见结构
金属晶体的常见结构有以下几种:
1. 面心立方(FCC)结构:在这种结构中,金属原子分别位于正方形面的角点和中心,以及正方形面的中心。
每个原子都与12个邻近原子相接触,形成一个紧密堆积的结构。
典型的例子是铜、铝和金。
2. 体心立方(BCC)结构:在这种结构中,金属原子分别位于正方体的角点和正方体的中心。
每个原子都与8个邻近原子相接触,形成一个比较紧密的结构。
铁和钨是常见的具有BCC结构的金属。
3. 密排六方(HCP)结构:在这种结构中,金属原子以一定的方式排列,形成六边形的密排层,其中每个层的原子位于前一层原子的空隙上。
这些层之间存在垂直堆叠,形成一个紧密堆积的结构。
典型的例子是钛和锆。
除了以上三种常见的金属晶体结构外,还有其他特殊的结构,如体心立方密堆积(BCC HCP)和面心立方密堆积(FCC HCP)等。
这些不同的结构对于金属的性质和行为有着重要的影响。
1。
金属晶体的结构

金属键
金属原子之间通过自由电子的流 动形成金属键,这种键合方式赋 予金属良好的导电性和延展性。
离子键
金属离子通过正负电荷的吸引形 成离子键,这种键合方式使得金 属具有良好的导电性和耐腐蚀性。
热力学条件对晶体结构的影响
温度
在高温下,金属原子运动速度快,容易形成 稳定的晶体结构;在低温下,原子运动速度 减缓,晶体结构不易形成。
金属晶体结构与性能关系
金属晶体结构与性能之间的关系是材料科学领域 的重要问题。未来研究可以深入探索金属晶体结 构与物理、化学性质之间的关系,为实现金属材 料的性能优化提供理论依据。
THANKS.
金属晶体在工业中的应用
导电材料
结构材料
由于金属晶体具有高电导率, 它们被广泛应用于制造电线、 电缆和电极等导电材料。
金属晶体具有较高的机械强 度和硬度,因此被广泛应用 于制造结构件,如桥梁、建 筑和航空航天器等。
散热材料
金属晶体的高热导率使其成 为理想的散热材料,广泛应 用于电子设备和计算机芯片 的散热。
详细描述
在体心立方结构中,每个原子位于立方体的中心,同时与八个最近的原子形成等边三角 形。这种结构具有较高的硬度,使得金属具有良好的抗冲击性能。常见的体心立方金属
包括铬、钨、铁等。
密排六方结构
总结词
密排六方结构是一种金属晶体结构,其 特点是每个原子周围有十二个最近邻原 子,排列紧密且规则。
VS
详细描述
金属晶体结构可以根据原子或分子的排列方式进行分类。常见 的金属晶体结构有面心立方、体心立方、六方密排等。
金属晶体结构的形成
金属晶体结构是在熔融态或固态下通过结晶形成的。在结晶过程中,原子或分 子的排列方式受到温度、压力等因素的影响,形成不同的金属晶体结构。
材料科学基础-第六章 金属材料的结构特征

kT
)] Q )]
式中K---比例常数 G*---形核功 Q-----原子越过液固界面的扩散激活能 K---波尔兹曼常数 T---热力学温度。
原子扩散的概率因子[exp( 因此形核率为 N K exp( G *
kT
)
kT
exp(
Q
kT
6.1
纯金属的凝固及结晶
由上式可知,要使Gv<0,必须使T>0,即T<Tm, 故T称 为过冷度。晶体凝固的热力学条件表明,实际凝固温度 应低于熔点,即需要有过冷度。
6.1
纯金属的凝固及结晶
6.1.1 晶体凝固的热力学条件
纯金属晶体的凝固是通过形核和长大两个过程进行的,成核 分成均匀成核和非均匀成核。
均匀形核:新相晶核是在母相中均匀生成的,即晶核 由液相中的一些原子团直接形成,不受杂质粒子或外 表面的影响。 非均匀(异质)形核:新相优先在母相中存在的异质 处形核,即依附于液相中的杂质或外来表面形核。
6.1
纯金属的凝固及结晶
6.1.1 晶体凝固的热力学条件 (一)均匀成核 1. 晶体形成时的能量变化和临界晶核 假定晶胚为球形,半径为r,当过冷液中出现一个晶胚时, 总的自由能变化G应为:
4 3 G r Gv 4r 2 3
式中,为比表面能,可用表面张力表示。
6.1
纯金属的凝固及结晶
其中NT是晶体在界面上可排列原子位置的数量 Tm是晶体的熔点 k是玻尔茨曼常数
6.1
纯金属的凝固及结晶
6.1.2 晶体长大 (一)液-固界面的构造
液-固界面的Jackson模型 ΔSm为熔化熵, ξ=η/ν,η为界面原子平均配位数 ν为晶体配位数, 所以ξ<1
金属晶体课件
电子工业领域应用案例
集成电路制造
01
金属晶体在集成电路制造中发挥着重要作用,用于制造芯片内
部的连接线路和引脚。
电子元器件制造
02
金属晶体在电子元器件制造中,如电阻、电容、电感等,作为
电极或支撑结构。
传感器与执行器
03
金属晶体在传感器和执行器中,如热敏电阻、磁敏元件等,用
于实现信号转换和调控。
汽车工业领域应用案例
金属晶体课件
目 录
• 金属晶体概述 • 金属晶体结构 • 金属晶体相图与相变 • 金属晶体制备方法与技术 • 金属晶体应用领域及案例分析 • 金属晶体未来发展趋势与挑战
01
CATALOGUE
金属晶体概述
定义与分类
定义
金属晶体是由金属原子或离子通 过金属键结合形成的晶体结构。
分类
根据金属键的类型,金属晶体可 分为简单金属晶体和复杂金属晶 体。
六方密排晶格
以钛、锆、铪等金属为代 表,具有特殊的紧密堆积 结构。
晶体结构与性能关系
力学性能
晶体结构对金属的力学性能如硬 度、韧性、抗拉强度等有显著影
响。
物理性能
晶体结构对金属的物理性能如导电 性、导热性、磁性等有不同程度的 影响。
加工性能
晶体结构对金属的加工性能如铸造 、轧制、锻造等有重要影响。
在晶体中自由移动。
延展性
金属晶体具有较好的延展性, 可以加工成各种形状的金属制
品。
金属光泽
金属晶体具有独特的金属光泽 ,这是由于金属表面的自由电 子与光子相互作用产生的。
热膨胀性
金属晶体在加热时,其体积会 发生变化,表现出热膨胀性质
。
02
CATALOGUE
安徽安徽高中化学竞赛无机化学第六章晶体结构基础
安徽安徽高中化学竞赛无机化学第六章晶体结构基础6. 0. 01 晶体的四种差不多类型:依照晶体中微粒之间相互作用的性质,能够将晶体分成4种差不多类型:离子晶体、金属晶体、分子晶体和原子晶体。
6. 1. 01 分子晶体及其物理性质:分子之间以分子间作用力结合成的晶体称为分子晶体。
由于熔、沸点较低,因此分子晶体一样要在较低的温度下才能形成,而在常温时多以气体形式存在。
分子晶体的硬度较小,导电性能一样较差,因为电子从一个分子传导到另一个分子专门不容易。
6. 1. 02 极性分子:分子的正电荷重心和负电荷重心不重合,则为极性分子。
6. 1. 03 偶极矩:极性分子的极性能够用偶极矩m 来度量。
若正电荷(或负电荷)重心上的电荷量为q,正、负电荷重心之间距离即偶极长为d,则偶极矩m = q d6. 1. 04 偶极矩的单位:当d = 1.0 ´10-10 m,即d 为 1 ,q = 1.602 ´10-19 C,即q 为电子的电荷量时,偶极矩m = 4.8 D。
D 为偶极矩单位,称为德拜。
在国际单位制中,偶极矩m以C•m(库仑•米)为单位,当q = 1 C,d = 1 m时,m = 1 C•m。
C•m 与D 这两种偶极矩单位的换算关系为= 3.34 ´10-30 C•m6. 1. 05 永久偶极:极性分子的偶极矩称为永久偶极,偶极矩的矢量方向由正极指向负极。
多原子分子中的大p 键及孤电子对,有时也阻碍分子的偶极矩。
6. 1. 06 诱导偶极:非极性分子在外电场的作用下,能够变成具有一定偶极矩的极性分子,如下面左图所示。
而极性分子在外电场作用下,其偶极矩也能够增大,如下面右图所示。
在电场的阻碍下产生的偶极称为诱导偶极。
6. 1. 07 阻碍诱导偶极的因素:诱导偶极强度大小与电场强度成正比,也与分子的变形性成正比。
所谓分子的变形性,即分子的正、负电荷重心的可分程度。
分子体积越大,电子越多,变形性越大。
高中化学课件 金属晶体结构
(3)六方晶胞:
在六方体顶点的微粒为6个晶胞共有,在面心的 为2个晶胞共有,在体内的微粒全属于该晶胞。 微粒数为:12×1/6 + 2×1/2 + 3 = 6
长方体晶胞中不同位置的粒子对晶胞的贡献: 顶点----1/8 棱----1/4 面心----1/2 体心----1
堆积方式及性质小结
①简单立方堆积 配位数 = 6 空间利用率 = 52.36% ② 体心立方堆积 ——体心立方晶胞 ③ 六方堆积 ——六方晶胞 ④面心立方堆积 ——面心立方晶胞 配位数 = 8 空间利用率 = 68.02% 配位数 = 12 空间利用率 = 74.05% 配位数 = 12 空间利用率 = 74.05%
练
习
1. 右图是钠晶体的晶胞结构, 则晶胞中的原子数是 8×1/8 +1=2 .
钠晶体的晶胞
2.合金有许多特点,如钠-钾合金 ( 含钾 50% ~80%)为液体,而钠钾的单质均为 固体,据此推测生铁、纯铁、碳三种物 质中,熔点最低的是 ( ) A. 生铁 (Fe与C的合金) B. 纯铁 C. 碳 D. 无法确定
5
4
面心立方堆积,配位数为12, 金、银、铜、铅等属于面心立方堆积,
顶点占1/8
棱上占1/4
面心占1/2
体心占1
2.晶胞中微粒数的计算
(1)体心立方:
在立方体顶点的微粒为8个晶胞共享,处于体 心的金属原子全部属于该晶胞。 微粒数为:8×1/8 + 1 = 2
(2)面心立方:
在立方体顶点的微粒为8个晶胞共有,在面心的 为2个晶胞共有。 微粒数为:8×1/8 + 6×1/2 = 4
熔点很高的金属:钨(3410℃)
铁的熔点:1535 ℃
金属材料金属的晶体结构全解.pptx
(2)冷形变金属的加工硬化
Ⅱ线性硬化阶段:位 错密度增加,其它滑 移系统被激活,形成 压杆位错,阻碍位错 的继续运动,从而产 生大的硬化效应
Ⅲ抛物线型硬化阶段: 滑移线变粗成滑移带, 新增加的应变几乎全 部集中在这些滑移带 内,且滑移带碎花。
Ⅰ易滑移阶段:加工 硬化主要来自位错的 增殖所引起的内应力
第7页/共38页
(1)晶胞中的原子数
顶点占1/8
棱占1/4
面心占1/2
体心占1
第8页/共38页
面心立方结构:
n=8×1/8+6×1/2=4
第9页/共38页
体心立方结构:
n=8×1/8+1=3
第10页/共38页
密排六方结构:
n=12×1/6+2×1/2+3=6
第11页/共38页
(2)点阵常数与原子半径的关系 点阵常数:晶胞的棱边长度(a,b,c)
第27页/共38页
点缺陷 (a)空穴;(b)间隙原子;(c)小取代原子;(d)大取代原子;
(e)Frenkel缺陷;(f)Schttky缺陷
第28页/共38页
2. 线缺陷
线缺陷就是晶体中的位错。按严格的几何意义, 位错是直径约5个原子的柱状缺陷,在晶体中以 各种方向延伸,不一定是直线。位错在金属材料 中大量存在,在自然生长的金属单晶中,每单位 平方厘米的面积就有106个位错穿过。
单晶体加工硬化3阶段示意图
第34页/共38页
3种典型的金属单晶体的应力-应变曲线
第35页/共38页
铝单晶与多晶体的应力-应变曲线比较(室温)
第36页/共38页
课堂作业
1. 试述原子间的键合方式,并举例说明。 2. 空间点阵的概念?空间点阵和晶体结构的关系? 3. 纯金属的晶体结构有哪些?并分析他们的特征 4. 金属晶体结构的缺陷? 5. 描述金属材料的形变过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立 方 F
二、 α-Fe型(A2)晶体 Fe原子按A2堆积(体心立方堆积)
每个原子的配位数为8 1套等同点 结构基元:Fe 空间点阵型式:立方I 每个晶胞中有2个Fe原子, 其坐标分别为: (0,0,0) (1/2,1/2,1/2)
晶 胞
•
立 方 I
三、 Mg型(A3)晶体
Mg原子按A3堆积(六方最密堆积) 每个原子的配位数12 2套等同点 结构基元:2个Mg 空间点阵型式:六方P 每个晶胞中有2个Mg原子, 其坐标分别为: (0,0,0), (1/3,2/3,1/2) 或 (0,0,0),(2/3,1/3,1/2)
2 layers
3 layers
把第三层 放在与第 一层一样 的位置 ABA Hexagonal close-packing (HCP)
把第三层 放在堵住 头二层漏 光的三角 形空隙上 ABC Cubic close-packing (CCP)
(1)ABCABC……, 即 每三层重复一次, 这种结构 称为A1 (或A1)型, 从中可以 取出立方面心晶胞;
(2)ABABAB……, 即每 两层重复一次, 称为A3 (或A3) 型, 从中可取出六方晶胞。
这两种最密堆积是金属单质晶体的典型结构.
A3堆积:ABAB……
A3最密堆积形成的六方晶胞
A3最密堆积形成后, 从中可以划分 出什么晶胞?
六方晶胞.
每个晶胞含2个原子(即8×1/8+1), 组成一个结构基元. 抽象成六方简单格子. 六方晶胞的c轴垂直于密置层:
6.2.3 非最密堆积结构
非最密堆积方式中最重要的是立方体心堆积A2 , 还有A4和少数的A6、A7、A10、A11、A12等.
A2 立方体心密堆积
布鲁塞尔的原子球博物馆 9个直径18米的球形展厅构成一个立方体心模型
A4 金刚石型结构
A4中原子以四面体键相连. 晶胞中虽然都是同种原子, 但所处的环境不同(球棍图中用两色颜色来区分). 一个浅蓝 色球与一个深蓝色球共同构成一个结构基元.
A1中:球数:八面体空隙数:四面体空隙数=1:1:2的图解
1. 指定中心一 个球G,即球数=1;
(为看得清楚,绿球 和蓝球层各有3个球 未画出)
2. G参与形成八面体空隙共6次. 其中第1-3次发生在绿球层与红球层之间:
第4-6次发生在红球层与蓝球层之间:
3. G每参与形成八面体1次, 它就对应着1/6个八面体. G共参与6次, 故对应着6 × 1/6 = 1 个八面体空隙.
第六章 金属晶体的结构
在元素周期表这个王国里,大约80%是 金属元素的领地. 使金属原子结合成金属的作用是金属 键. 金属键没有饱和性和方向性. 金属晶体 的物理性质和结构特点都与金属键密切相 关. 金属能带理论有助于理解金属的物理性 质.
6.1 金属能带理论-自学
固体能带理论是关于晶体的量子理论.对于金属中的 能带,常用的是“近自由电子近似(NFE)”模型和“紧束 缚近似(TBA)”模型. 虽然NFE比TBA更适用于简单金 属,但TBA更具有化学特色,它相当于分子中LCAO-MO 在晶体中的推广。
c
从ABAB……堆积中划分出六方晶胞, 可能使人感到困惑。 因为在一个密置层上, 通过球心处的旋转轴是六重轴, 通过三 角形空隙处的是三重轴:
密置层堆积起来后, 三重旋转轴总可以保留, 六重旋转轴却 不能继续保留:
六重旋转轴消失 三重旋转轴仍然保留
将局部放大看得更清楚:那么,“六方晶胞”又从何谈起呢?
ABCABC……堆积怎么会形成立方面心晶胞? 请来个逆向思维:
取一个立方面心晶胞: 体对角线垂直方向就是密置层, 将它们设成3种色彩:
从逆向思维你已明 白,立方面心晶胞确实满 足ABCABC……堆积。 那么, 再把思路正过来: ABCABC……堆积形成立 方面心晶胞也容易理解吧? 将视线逐步移向体对角线, 沿此线观察:
例. 25℃下,测得立方硅晶体的a=543.1066pm,密度为 2.328992g·cm-3,已知它属金刚石型结构,Si相对原子质量为 28.08541,求阿伏加德罗常数值。 解:立方硅晶体属金刚石型结构,晶胞中含有8个硅原 子,设阿伏加德罗常数用NA表示,则有下列关系式:
一个晶胞中硅原子的质量 晶胞体积 28.08541g ⋅ mol-1 8× NA -3 = = ⋅ 2.328922g cm (543.1066 × 10−10 cm)3 8 × 28.08541 23 NA = = 6.02 × 10 2.328922 × (543.1066 × 10−10 cm)3 硅晶体密度=
作业:8.11、8.13、8.16
4. G参与形成四面体 共8次. 其中, 第1-4次发生 在绿球层与红球层之间:
Hale Waihona Puke 第5-8次发生在红球 层与蓝球层之间:
5. G每参与形成四面体1次, 就对应着1/4个四面体. G共参与8次, 故对应着8 × 1/4 = 2 个四面体空隙.
结论: A1堆积中,球数:八面体空隙数:四面体空隙数=1:1:2. 仿照以上方法很容易证明 A3堆积中也有相同的关系.
若注意到六方晶系的特征对称元素——六次对称轴并不 限于六次旋转轴, 也包括六次反轴或六次螺旋轴. 就可以消除 这种困惑:
六次反轴
六次螺旋轴
A1型: ABCABC…
红、绿、蓝球是同一种原子,使用三种色球只是为了看清三层的关系 。
ABCABC…
垂直于密置层观察(俯视图)
平行于密置层观察(侧视图
A1最密堆积形成立方面心(cF)晶胞
6.2 金属单质的晶体结构
金属单质晶体结构比较简单, 这与金属键密切相关: 由 于金属键没有方向性和饱和性,大多数金属元素按照等径 圆球密堆积的几何方式构成金属单质晶体,主要有立方面 心最密堆积、六方最密堆积和立方体心密堆积三种类型.
6.2.1 等径圆球最密堆积与A1、A3型结构
等径圆球以最密集的方式排成一列(密置列),进 而并置成一层(密置层),再叠成两层(密置双层), 都只有一种方式: (说明:本章金属单质晶体的球堆积图上,球都是 同种原子,色彩只用来区别不同的密置层或不同环境)
6.2.5 小结: 几种典型的金属单质晶体结构
一、Cu型(A1)晶
Cu原子按A1堆积 每个原子的配位数为12 1套等同点 结构基元:Cu 空间点阵型式:立方F 每个晶胞中有4个Cu原子, 其坐标分别为: (0,0,0) (1/2,1/2,0) (1/2,0,1/2) (0,1/2,1/2)
晶 胞
密置双层
密置双层中有两种空隙: 正八面体空隙(由3A+3B构成) 正四面体空隙(由3A+1B或1A+3B构成)
一个晶胞
密置双层的晶胞中含1个正八面体空隙和2个正四面体空隙. 球数: 正八面体空隙数:正四面体空隙数=2:1:2
A1和A3最密堆积中的空隙
A1和A3中也只有正八面体和正四面体空隙. 为求出它们 与球数的比例, 原则上也是取一个晶胞, 对于球和两种空隙计数. 实际作起来却不易搞明白. 为此, 换一种方法来理解: 指定一个球(球数为1), 观察它参 与形成正八面体空隙的次数, 每参与一次, 它就对应着1/6个正 八面体空隙. 对正四面体空隙也依此类推, 只不过每参与一次对 应着1/4个正四面体空隙.
等径圆球的密堆积
密置层如何叠起来形成密堆积? 先考察一个密置层的结构特点:
从一个密置层上,可以看出这样几点: 1. 层上有3个特殊位置: 球的顶部A、上三角空隙B和下三角空隙 C. 以该层为参照层,称为A层; 2. 叠加到A层上的第二层各个球只能置于空隙B或C. 由于上下三角 是相对而言, 故称第二层为B层; 3. 第三层叠加到第二层B上时,只可能是C或A层; 4. 无论叠加多少层,最多只有A、B、C三种, 最少有A、B两种(因为 相邻层不会同名); 5. 若以后各层均按此方式循环, 每三层重复一次,或每两层重复一 次,就只会产生两种结构:
6.2.4 空间利用率
空间利用率=晶胞中原子总体积 / 晶胞体积 用公式表示: P0=Vatoms/Vcell
A1 空间利用率的计算
这是等径圆球密堆积所能达到的 最高利用率,所以A1堆积是最密堆积.
A3
空间利用率的计算
A2 空间利用率的计算
A4 空间利用率的计算
8r 3a = 8 r → a = 3 4 3 32 3 Vatoms = πr × 8 = πr 3 3 3 r r 512 8 Vcell = a 3 = ( ) 3 = 3 3 3 Vatoms 3π Po = = = 34.01% Vcell 16
晶胞
六方P
四、 金刚石型晶体(A4型)
C原子的配位数为4, 2套等同点 结构基元:2个C 空间点阵型式:立方F 每个晶胞中有8个C原子, 其坐标分别为: (0,0,0), (1/2,1/2,0), (1/2,0,1/2),(0,1/2,1/2), (1/4,1/4,1/4),(1/4,3/4,3/4), (3/4,1/4,3/4),(3/4,3/4,1/4)
你看到的正是ABCABC……堆积!
6.2.2 最密堆积结构中的空隙类型
球堆积决不可能将空间完全填满, 必然要留下空隙. 下面将由简到繁地讨论空隙数目与球的数目有什么关系.
在一个密置层中, 有上三角形与下三角形两种空隙:
从一个平行四边形正当格子可看出, 球数 : 上三角形空隙 数:下三角形空隙数=1 : 1 : 1, 或者说球数 : 三角形空隙数 2
