场强电势习题课
静电场——电场强度和电势

库仑定律 电场强度1、实验定律a 、库仑定律条件:⑴点电荷,⑵真空,⑶点电荷静止或相对静止。
事实上,条件⑴和⑵均不能视为对库仑定律的限制,因为叠加原理可以将点电荷之间的静电力应用到一般带电体,非真空介质可以通过介电常数将k 进行修正(如果介质分布是均匀和“充分宽广”的,一般认为k′= k /εr )。
只有条件⑶,它才是静电学的基本前提和出发点(但这一点又是常常被忽视和被不恰当地“综合应用”的)。
b 、电荷守恒定律c 、叠加原理2、电场强度a 、电场强度的定义电场的概念;试探电荷(检验电荷);定义意味着一种适用于任何电场的对电场的检测手段;电场线是抽象而直观地描述电场有效工具(电场线的基本属性)。
b 、不同电场中场强的计算决定电场强弱的因素有两个:场源(带电量和带电体的形状)和空间位置。
这可以从不同电场的场强决定式看出⑴点电荷:E = k 2rQ ⑵证明:均匀带电环,垂直环面轴线上的某点电场强度E =2322)R r (k Qr +⑶证明:均匀带电球壳a.内部某点电场强度大E 内= 0b.外部外部距球心为r 处场强为E 外 = k 2rQc.如果球壳是有厚度的的(内径R 1 、外径R 2),在壳体中(R 1<r <R 2)E = 2313rR r k 34-πρ ,其中ρ为电荷体密度。
⑷证明:无限长均匀带电直线(电荷线密度为λ):E = rk 2λ⑸证明:无限大均匀带电平面(电荷面密度为σ):E = 2πk σ3.电通量和高斯定理(1)电通量:在电场中穿过任意曲面的电场线的总条数称为穿过该面的电通量,用 Ф 表示。
E 与平面S 垂直时,Ф=ESE 与平面S 有夹角θ时,θcos ES Φe =(2该曲面所包围的所有电荷电量的代数Σq i 和除以 ε0 ,荷无关.练习:用高斯定理证明上述(3)、(4)、(5)内的结论练习1.半径为R 的均匀带电球面,电荷的面密度为σ,试求球心处的电场强度。
⊥E2.有一个均匀的带电球体,球心在O 点,半径为R ,电荷体密度为ρ ,球体内有一个球形空腔,空腔球心在O ′点,半径为R ′,O O = a ,如图7-7所示,试求空腔中各点的场强。
电势和电场强度练习

电势和电场强度练习一、单选题1.以下关于电场性质的叙述,正确的是A .电场线越密的地方,电势越高B .电场中某点的场强大小数量上等于单位电量的电荷在该点所受电场力的大小C .电场中同一等势面上的各点电势和场强均相同D .正点电荷或负点电荷形成的电场,都有离点电荷越近,场强越小的规律2.静电场中有M 、N 两点,已知M 点的电势高于N 点的电势,则下面说法中正确的是 A .M 点与N 点连线方向就是电场线方向B .一个点电荷在M 点受的电场力总要大于在N 点处受到的电场力C .M 点的电场强度一定大于N 点的电场强度D .一个正点电荷从N 点移到M 点,它的电势能一定增加3.关于电场强度、电势、电势差和等势面,下列说法正确的是A .电场强度为零处电势一定为零B .电势为零处电场强度一定为零C .在匀强电场中,同一条直线上两点间的电势差与这两点间的距离成正比D .在电场中,任意两相邻的等势面(电势差相等)之间的距离相等4.如图,A 、B 、C 是一条电场线上的三点,已知AB =BC ,则下列说法正确的是A .场强大小关系一定有ABC E E E ==B .电势大小关系一定有A BC ϕϕϕ>>C .电势差大小关系一定有AB BC U U =D .负电荷在A 、B 、C 三点所具有的电势能大小关系有p p p A B CE E E >>5.在电场中,A 、B 两点间的电势差100V AB U =,B 、C 两点间的电势差160V BC U =−,则A 、B 、C 三点电势高低关系为A .ABC ϕϕϕ>> B .A C B ϕϕϕ<<C .C A B ϕϕϕ>>D .C B A ϕϕϕ>>6.如下图所示,匀强电场场强100V /m E =,A 、B 两点相距10cm ,A 、B 连线与电场线夹角为60°,则AB U 之值为A .5VB .C .10VD .-10V 7.某电场等势面如图所示,图中a 、b 、c 、d 、e 为电场中5个点,则A .一电子从b 点运动到e 点,电场力做正功B .一电子从d 点运动到a 点,电场力做功为4eVC .b 点电场强度垂直于该点所在等势面,方向向左D .a 、b 、c 、d 、e 五个点中,e 点的电场强度大小最小8.在匀强电场中,将电荷量为6310C −−⨯的点电荷P 从电场中的A 点移到B 点,静电力做了52.410J −⨯的功,再从B 点移到C 点,静电力做了51.210J −−⨯的功。
电势差、电势差与场强的关系习题课

电势差、电势差与电场强度的关系 习题课制作人:练中天 审核:刘红梅知识点一:电场力做功的特点和计算方法1、 电场力做功与电荷电势能变化的关系 电荷在电场中任意两点间移动时,它的电势能的变化情况是确定的,因而移动电荷电场力做功的值也是确定的,即电场力的功等于电势能的减少量。
2、 电场力做功的计算(1) 由功的定义式a Fl W cos =计算,要求式中F 为恒力,所以此方法仅适用于匀强电场中电场力做功的计算。
(2) 用结论”电场力的功等于电势能的减少量”来计算,即 21P P E E W -=,这个方法在已知初末位置的电势能或电势的情况下应用比较方便。
(3) 用公式ABqUW =来计算,此时,一般又有两种方法:一是严格带符号运算,q 和U AB 均考虑正和负,所得W 的正负直接表示电场力做功的正负;二是只带入绝对值进行计算,所以W 只是功的数值,至于功的正负,可用力学知识判定。
(4) 用动能定理:K E W W ∆=+其他电进行计算。
它是动能定理在电场中的应用,适用于任何电场中电场力做功的计算。
一般知道电荷运动的情况时,如知道初末位置的速度,用此种方法较简便。
【例1.】在电场中把92.010C -⨯ 的正电荷从A 点移到B 点,静电力做功71.510J -⨯ 。
再把这个电荷从B 点移到C 点,静电力做功 74.010J --⨯ 。
①A 、B 、C 三点间哪点电势最高? ②A 、B 间,B 、C 间,A 、C 间的电势差各是多大? ③把 91.510C --⨯ 的电荷从A 点移到C 点,静电力做功多少?解:①电荷从A 点移动到B 点,静电力做正功,所以A 点的电势比B 点高。
电荷从B 点移动到C 点,静电力做负功,所以C 点电势比B 高。
但C 、B 间电势差的绝对值比A 、B 间电势差绝对值大,所以C A B ϕϕϕ〉〉 ②根据AB AB W U q=,A 、B 间电势差791.510752.010AB AB W U V V q--+⨯===+⨯A 点电势比B 点高75V , 794.0102002.010BC BC W U V V q---⨯===-+⨯,C 点电势比B 点高200VA 、C 间电势差75200125AC AB BC U U U V =+=-=- ③电荷从A 点移动到C 点时,静电力做功为'97( 1.510)(125) 1.87510AC AC W q U J --==-⨯⨯-=⨯知识提炼:1、电场中两点间的电势差,有电场本身的决定,与在这两点间移动的电荷的电量、静电力做功的大小无关,在确定的电场中,既是不放电荷,任何两点间的电势差都有确定的值。
电场强度电势电势能习题经典

电场强度、电势、电势能专题1、关于静电场场强的概念,下列说法正确的是()A.由E=F/q可知,某电场的场强E与q成反比, 与F成正比B.正、负检验电荷在电场中同一点受到的电场力方向相反,所以某一点场强方向与放入检验电荷的正负有关C.电场中某一点的场强与放入该点的检验电荷正负无关D.电场中某点不放检验电荷时,该点场强等于零2、电场强度的定义式为E=F/q,下列说法正确的是()A.该定义式只适用于点电荷产生的电场B.F是检验电荷所受到的力,q是产生电场的电荷电量C.场强的方向与F的方向相同D.由该定义式可知,同一点电荷在电场中某点所受的电场力大小与该点场强的大小成正比3、关于电势的高低,下列说法正确的是( )A.沿电场线方向电势逐渐降低B.电势降低的方向一定是电场线的方向C.正电荷在只受电场力作用下,一定向电势低的地方运动D.负电荷在只受电场力的作用下,由静止释放时,一定向电势高的地方运动5、下列关于电场性质的说法,正确的是( )A.电场强度大的地方,电场线一定密,电势也一定高B.电场强度大的地方,电场线一定密,但电势不一定高C.电场强度为零的地方,电势一定为零D.电势为零的地方,电场强度一定为零6、关于电势与电势能的说法,正确的是( )A.电荷在电势越高的地方,电势能也越大B.电荷在电势越高的地方,它的电荷量越大,所具有的电势能也越大C.在正点电荷的电场中任一点,正电荷所具有的电势能一定大于负电荷所具有的电势能D.在负点电荷的电场中任一点,正电荷所具有的电势能一定小于负电荷所具有的电势能7、如图所示的电场线,可判定( )A.该电场一定是匀强电场第7题图B.A点的电势一定低于B点电势C.负电荷放在B点的电势能比放在A点的电势能大D.负电荷放在B点所受电场力方向向右8、有关等势面的说法中正确的有( )A 、等势面一定与电场线垂直,即跟场强的方向垂直.B 、电场线总是由电势高的等势面指向电势低的等势面,两个不同的等势面永远不会相交.C 、两个等势面间的电势差是相等的,但在非匀强电场中.两个等势面间的距离并不恒定,场强大的地方.两等势面间的距离小,场强小的地方,两个等势面间的距离大。
电磁学习题课lesson16
dfe dt
Ñò òò v v
H × dl
l
= Is
=
S
æ ç è
v j传导
+
v dD dt
ö ÷ ø
×
v dS
10
作业1分析
作业二: 1、如图所示,两个同心的均匀带电球面,内球面半径为 R1,带电量 Q1,外球面半径为 R2,带电量为 Q2。设无穷远处为电势零点。 求: (1) 空间各处电场强度的分布;
答:是等势体 如果把导体一分为二,两部分的电势不相等
14
3、当一个带电导体达到静电平衡时,表面曲率较大处电荷密度较大,故
其表面附近的场强较大。
( ×)
孤立导体达到静电平衡表面场强大小为 E = s e0
作业2平行板电容器,两极板面积均为 S,板间距离为 d( d远 小于极板线度),在两极板间平行地插入一面积也是S、厚度为 t(< d) 的金属片。 试求: (l)电容C等于多少? (2)金属片放在两极板间的位置对电容值有无影响?
20
3、一宽b=2.0cm,厚d=1.0mm的铜片,放在B=3.0T的磁场中,磁场垂 直通过铜片,如果铜片载有电流100A,已知铜片中自由电子的密度 是 n=8.4´1028m-3 求此时产生的霍耳电势差的大小是多少?
作业五:
UH
= RH
BI d
=1 nq
BI d
=
8.4
´1028
3´100 ´1.6 ´10-19
2、以下说法正确的是( A ) (A) 在电势不变的区域内,电场强度一定为零 (B) 在电势为零处,场强一定为零 (C) 场强为零处,电势一定为零 (D) 在均匀电场中,各点电势相等
13
3、在均匀电场中,各点的( B )
第51讲 匀强电场中的场强、电势、电势能的定性分析与定量计算(解析版)

第51讲匀强电场中的场强、电势、电势能的定性分析与定量计算1.(2021•全国)如图,P、Q、M、N为菱形的四个顶点。
若已知该空间存在一方向与此菱形平面平行的匀强电场,则()A.P、Q、M、N四点中至少有两点电势相等B.P、Q、M、N四点可能位于同一等势面上C.P、Q间的电势差一定与N、M间的电势差相等D.P、Q间的电势差一定与Q、M间的电势差相等【解答】A.过Q点做PN的垂线,交于O点,当电场方向垂直于QO,则QO为一条等势线,匀强电场中,各等势线互相平行,则P、Q、M、N四点电势都不相等,故A错误;B.匀强电场的等势面是与电场方向垂直的平面,则P、Q、M、N四点不可能位于同一等势面上,故B错误;C.由图可知,PQ与NM平行且相等,则PQ与NM沿电场线方向的距离相等,根据U=Ed可知U PQ=U NM故C正确;D.如果电场方向垂直于PO,则PQ为等势线,则U PQ=0则电场线与QM不垂直,则QM不是等势线,则U QM≠0故D错误。
故选:C。
(多选)2.(2021•河北)如图,四个电荷量均为q (q>0)的点电荷分别放置于菱形的四个顶点,其坐标分别为(4l,0)、(﹣4l,0)、(0,y0)和(0,﹣y0),其中x轴上的两个点电荷位置固定,y轴上的两个点电荷可沿y轴对称移动(y0≠0)。
下列说法正确的是()A.除无穷远处之外,菱形外部电场强度处处不为零B.当y0取某值时,可使得菱形内部只存在两个电场强度为零的点C.当y0=8l时,将一带负电的试探电荷由点(4l,5l)移至点(0,﹣3l),静电力做正功D.当y0=4l时,将一带负电的试探电荷放置在点(l,l)处,其所受到的静电力方向与x轴正方向成45°倾斜向上【解答】解:A、在菱形外侧除无穷远处的任意点,四个点电荷在该点的产生的场强均指向菱形的外侧,根据场强的叠加原理可知,合场强不可能为零,所以除无穷远处之外,菱形外部电场强度处处不为零,故A正确;B、根据场强的叠加及对称性,在O点场强为零,当y0取某值时,由对称性可知,在菱形内部其它场强为零的点必定会成对出现,即在菱形内部场强为零的点一定是奇数个,故B错误;C、根据对称性知,(0,﹣3l)和(0,3l)处场强大小相等,方向相反,两点电势相等,将试探电荷由点(4l,5l)移至点(0,3l),在点(4l,5l),负电荷所受的电场力方向斜向左下方,在(0,3l)处,由于该点到x轴上4l、﹣4l以及y轴上8l的点的距离相等为5l,此三处点电荷在该点(0,3l)的场强大小相等,它们在此处合场强方向沿y轴向上,y轴上﹣8l处的点电荷在(0,3l)处产生的场强方向也沿y轴向上,则(0,3l)的场强方向沿y轴向上,则负电荷在该点所受的电场力方向沿y轴向下,所以一带负电的试探电荷从(4l,5l)沿直线移至点(0,3l),静电力一直做正功,可知将一带负电的试探电荷由点(4l,5l)移至点(0,﹣3l),静电力做正功,故C正确;D、当y0=4l时,根据对称性知,x轴和y轴上﹣4l处的点电荷在点(l,l)处产生的场强大小相等为E1=kq r12,r12=(5l)2+l2=26l2这两个点电荷的合场强E′1=2E1cosα由几何关系知:cosα=3√2l r 1=3√2l √26l =3√13 解得E′1=13√13l 2,方向与x 轴正方向成45°斜向上,同理:x 轴和y 轴上4l 处的点电荷在点(l ,l )处产生的场强大小相等为E 2=kq r 22, r 22=(3l)2+l 2=10l 2这两个点电荷的合场强E ′2=2E 2cos β由几何关系知:cosβ=√2l √r =1√5解得E′2=5√5l 2,方向与x 轴负方向成45°斜向下,可知:E ′2>E ′1,则点(l ,l )处产生的场强方向与x 轴负方向成45°斜向下,则负的试探电荷在该点所受的静电力方向与x 轴正方向成45°倾斜向上,故D 正确。
第一章(5)习题课
∴
E
0,
( r R)
E的方向垂直轴线沿径向, > 0则背离轴线;
R ˆ, ( r R ) r 0r
< 0则指向轴线。
11、无限大的均匀带电平面,电荷面密度为,P点与 平面的垂直距离为d,若取平面的电势为零,则P点的 电势 V p d / 2 0 ,若在P点由静止释放一个电子(其 质量为m,电量绝对值为e)则电子到达平面的速率为:
3、一均匀静电场,场强 E (400i 600 j )V m 1 , 则点a(3、2)和点b(1、0)之间的电势差为 Vab 2000V
解 : E 400i 600 j
b b a a
dl dxi dyj
Vab E dl (400i 600 j ) (dxi dyj )
侧 面 EdS E 侧 面 dS 2πrhE
(1) r < R时,
qi 0 ,
qi 由高斯定理 Φ ε0
即 2πrhE 0, 得 E 0 (2) r > R时, q i 2πRhσ ,
qi 由高斯定理 Φ ε0
σR 即 2πrhE 2πRhσ / ε0 , 得 E ε0 r
2
10.( 第一章习题二 .9) 无限长均匀带电圆柱面,电荷 面密度为,半径为R,求圆柱面内外的场强分布。
解:作一半径为r,高为h的同轴圆柱面
R r
E
为高斯面, 根据对称性分析,圆柱面 侧面上任一点的场强大小相等, 方向
h E
S
ˆ r
沿矢径方向。 Φ S E dS 上底 E dS 下底 E dS 侧面 E dS
大学物理场强电势习题课讲解
E 2 0 r
L
r ●P
r >>L
●
当 r > > L 时,带电圆柱面可 视为点电荷,其场强大小为: q L E 2 2 4 0 r 4 0 r
P
6、 (学习指导p165,17) A、B为真空中两个平行的 “ 无限大”均匀带电平面,已知两平面间的电场 强度大小为E 0 ,两平面外侧电场强度大小都为E0/ 3,方向如图。则A、B两平面上的电荷面密度分别 为 σA = , σB = . A B 若A 、B同号,则两边强中间弱。 若A正B负,则中间场强向右。 ∴只能是A负B正,则 E0 / 3
3真空中平行放置两块大金属平板板面积为s板间距离为dd远小于板面线度板上分别带电量q因板间距离d远小于板面线度金属平板可视为无限大带电平面两板间的相互作用力等于其中一块平板受另一平板在该板处产生的电场的作用力
1、真空中一点电荷Q,在距它为r的a点处有一试 验电荷q,现使q从a点沿半圆弧轨道运动到b点, 则电场力作功为( )
A B E0 2 0 2 0 B A E0 2 0 2 0 3
E0 2 0 E 0 A 3 4 0 E 0 B 3
E0 / 3
7、如图, 一点电荷带电量 q = 10 -9 C. A、B、C 三点分别距离点电荷 10cm、20cm、30cm .若选 B 点电势为0,则 A 点电势为___,C 点电势 为___.(0= 8.85 × 10-12 C2· N-1 · m-2 )
解: 利用电势的定义: q o
B A
A
B
C
r
B
当UB = 0 时,
q
r B U A E dr Edr A
【精准解析】高中物理人教版选修3-1教师用书:第1章+习题课1 电场的性质+Word版含解析
习题课1电场的性质(教师用书独具)[学习目标] 1.理解描述电场力的性质物理量——场强及电场线。
2.理解描述电场能的性质的物理量——电势、电势能、电势差及等势线。
一、电场线、等势面和运动轨迹的综合1.已知等势面的形状分布,根据电场线和等势面相互垂直可以绘制电场线。
2.由电场线和等差等势面的疏密,可以比较不同点的电场强度大小,电场线或等势面密集处,电场强度较大。
3.根据电荷的运动轨迹可以判断电荷受力方向和做功的正负,从而判断电势能的变化情况,注意静电力与电场线相切,且指向曲线的凹侧。
【例1】(多选)某同学在研究电子在电场中的运动时,得到了电子由a点运动到b点的轨迹(如图中实线所示),图中未标明方向的一组虚线可能是电场线,也可能是等势面,则下列说法正确的是()A.如果图中虚线是电场线,电子由a点运动到b点,动能减少,电势能增加B.如果图中虚线是等势面,电子由a点运动到b点,动能增加,电势能减少C.不论图中虚线是电场线还是等势面,a点的电场强度都大于b点的电场强度D.不论图中虚线是电场线还是等势面,a点的电势都高于b点的电势BC[若虚线是电场线,从轨迹弯曲方向可知电场力沿着电场线向左,ab曲线上每一点的瞬时速度与电场力方向均成钝角,故电子做减速运动,所以A错误;若虚线为等势面,根据等势面与电场线处处垂直可大致画出电场线,显然可看出曲线上每个位置电子受到的电场力与速度成锐角,电子加速运动,所以B正确;若虚线是电场线,由电场线的密集程度可看出a点的场强较大,由沿着电场线方向电势越来越低可判断a处的电势较高,若虚线是等势面,从电子曲线轨迹向下弯曲可知电场线方向垂直虚线向上,沿着电场线方向电势越来越低,故a点电势较小,可判断D错误;而等差等势面密集处电场线也越密集,故a处场强较大,因此无论虚线是电场线还是等势面,均有a点的场强大于b点的场强,所以C正确。
故选B、C。
]已知等势面的形状分布,根据电场线和等势面相互垂直绘制电场线,再根据轨迹弯曲方向找电荷的受力方向,结合运动轨迹或路径,判断功的正负;由静电力做功正负确定动能及电势能的变化。
场强和电势计算练习
1. 下列说法正确的是:A. 闭合曲面上各点电场强度都为零时,曲面内一定没有电荷;B. 闭合曲面上各点电场强度都为零时,曲面内电荷的代数和必定为零;C. 闭合曲面的电通量为零时,曲面上各点的电场强度必定为零;D. 闭合曲面的电通量不为零时,曲面上任意一点的电场强度都不可能为零。
(B)2. 判断下列说法正确与否A. 电场强度为零的点,电势也一定为零;B. 电场强度不为零的点,电势也一定不为零;C. 电势为零的点,电场强度也一定为零;D. 电势在某一区域为常量,则电场强度在该区域内必定为零;E. 电场强度相等的区域内,电势必定处处相等。
(D)3. 两条无限长平行带电直导线相距为0r ,均匀带有等量异号电荷,电荷线密度为λ.(1)求两导线构成的平面上任一点的电场强度(设该点到其中一线的垂直距离为x );(2)求每一根导线上单位长度导线受到另一根导线上电荷的电场力。
解:(1)设两根导线在P 点产生的电场分别用E +和E -表示(如图所示),其中 02E i xλπε+=,002()E i r x λπε-=-所以,按照场强叠加原理可得()00022P E E E i x r x λλπεπε+-⎛⎫=+=+ ⎪ ⎪-⎝⎭002()r i x r x λπε=-(2)设F +和F -分别表示正、负带电导线单位长度所受的电场力,则有2000()2F E r i r λλπε+-==, 2000()2F E r i r λλπε-+=-=-由此可知F F +-=-,二力大小相等,方向相反,这一对导线相互吸引。
4. 设在半径为R 的球体内,其电荷为球对称分布,电荷体密度为⎩⎨⎧>=≤≤=)(0)0(R r R r kr ρρ,k为一常量,试分别用高斯定理和电场叠加原理求电场强度与r 的关系。
PE +E解法1:由于电荷呈球对称分布,所以分析得出电场的分布亦呈球对称分布,选任意半径为r 的同心球面为高斯面,有24r E S d E Sπ⋅=⋅⎰在球体内(R r ≤≤0),4024kr dr rkr dV q rr iππρ===⎰⎰∑所以由高斯定理0ε∑⎰=⋅iSqS d E有424εππkr r E =⋅所以球体内的场强分布为rrkr E 024ε= (R r ≤≤0)在球体外(R r >),4204kR dr r kr dV q RRi ππρ===⎰⎰∑ 所以由高斯定理0ε∑⎰=⋅iSqS d E有424εππkR r E =⋅所以球体外的场强分布为r rrkR E 2044ε= (R r ≤≤0) 解法2:利用电场叠加法,将带电球体分割成无数多个同心带电球壳,球壳的带电量为'2''4dr r kr dV dq πρ==由上述分析,在球体内(R r ≤≤0),02202''0444επεπkr r dr r kr dE E rr ===⎰⎰ 所以球体内的场强分布为rrkr E 024ε= (R r ≤≤0)在球体外(R r >),204202''0444r kR r dr r kr dE E RR επεπ===⎰⎰ 所以球体外的场强分布为rrr kR E 2044ε= (R r ≤≤0)5. 电荷面密度分别为σ+和σ-的两块“无限大”均匀带电的平行板,如图放置,取坐标原点为零电势点,求空间各点的电势分布并画出电势随位置坐标x 的变化曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dU
解:(1)环形电荷元在p点的电势
2rdr
4 0 ( r h )
2 2 1 2
p X
R2
h
则整个圆环在p点的电势为
Up
E
er 20 r
都不满足n>1的条件,场强对于无限远处的积分都是发散的。 因此对这类 n≤1 的情况不能选择无限远为电势的0点,通常选带 电平面上的电位为零,或带电直线上的电位为零。 点电荷: E 1 2
r
可以选无限远为0点,但不能把0点选 在点电荷上,否则也会出现场中各点 电位为无限大的困难。
a
a
2
P
P
r
r r E1 E2 P 0 方向 0 P 方向 3 0 3 0 a E E1 E2 [r ( r )] 3 0 3 0 此结果说明空腔内的场强为均匀场方向由 0 0
对! 错! 错! 错!
(5)将高斯面外一个点电荷在外面移动,通过高斯面的电通量 将发生变化,面上电场也将变化; 错
(6)将高斯面外一个点电荷移入高斯面内,通过高斯面的电通 量将发生变化,面上电场也将变化. 对 qi内 i E d S
S
0
2. 真空中两个相对的平行板,相距为d,面积为S,分别带+q 和 -q的电量,有人说根据库仑定律,两板间的作用力为
静止电荷的电场
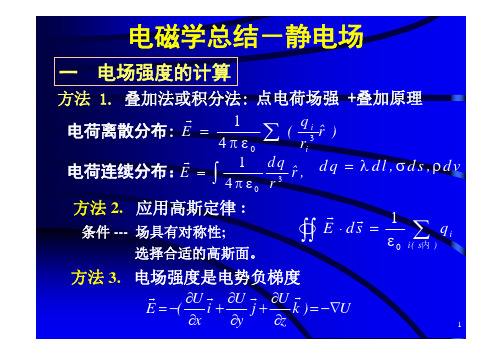
电势
习题课
1 .掌握电场强度、电通量的概念正确理解场强叠加原理. 2 .掌握用点电荷场强公式及场强叠加原理求场强的方法 . 3 .正确理解高斯定理.掌握用求高斯定律场强的方法.
4 . 理解静电场的保守性. 掌握电势差电势的概念,掌握
电势叠加原理.
5. 掌握已知电荷分布求电势的方法.
6 . 掌握电势与场强的积分关系, 理解电势与场强 的微分关系.
解: 选取某一距带电直导线为r0的点p0
无限长均匀带电直线的电场中的电势分布. E 已知E分布为: 20 r
r
为电势零点,则距带电直线为r的 p点的电势
dr p 2 r 0 p p' p dr E dl E dl 0 p ' 2 r p p' 0 lnr lnr0 ln r C 20 20 20
AB
E dl
B A
AAB q0 AB
q 0 E dr
A
B
课堂讨论题
1.若一个高斯面内电荷的代数和为零,判断下列说法是否正确: (1)穿过整个高斯面的电通量为零; (2)穿过高斯面上每个面元的电通量为零; (3)高斯面内没有电荷; (4)高斯面上各点的电场强度为零;
3 .已知电荷分布求场强的方法
(1) 点电荷电场的叠加 (2) 高斯定理求特殊对称电荷电场
(3) 已知电荷电场的分布,叠加求较复杂电荷电场.
(4) 已知电势的分布,用微分(梯度)求电场强度.
4 .已知电荷分布求电势的方法
(1) 点电荷电势的叠加 (2) 利用电场强度的线积分
p0
P
p
E dl
rA
E外=- R3/ 30r2
2 r R R / 2 3 0 dr 8 0
R
R R UB dr 2 2 R 3 r 6 0 0
R 3
2
R U A U B 7 24 0
2
取无限远处U=0
R
B
C
A
- O
R
r R3 UA dr dr 2 R/ 2 R 3 0 3 0 r
4.电势零点的选择是完全任意的吗?对无限长带电线或无限 大带电面的电场,可否选在无限远?点电荷的电场,可否选在 电荷上?说明理由并讨论:
如图一个面电荷密度为 的无限大平面,旁边距 离为a的位置有一个点电荷q,点电荷到平面的垂线中 点p的电势Up,有人用叠加原理计算为:
q a p , 40 ( a / 2) 2 0 2
r 2 11 24 0 3 3 R R U B E外 dr dr 2 rB 2R 3 0 r 6 0
R 2 U A U B 7 24 0
可见电势差与零点的选择无关.
q 2 2 1/ 2 4 ( x R ) 求:(1)圆环轴线p点的电势,与无孔金属圆板比较高低; 0
(4)均匀带电圆环轴线上
E
qx i 2 2 3/ 2 40 ( x R )
x x 2 R2 )i
q 2 2 1/ 2 40 ( x R )
( x 2 R2 x) 2 0
(5)均匀带电圆盘轴线上
E (1 2 0
6.电势差 7. 电场力的功
R2
R1
2 2 dU ( R2 h2 R1 h2 ) 2 0
若R1=0,即成为圆盘,则
2 U p ( R2 h2 h) 2 0 金属板的电势电势升高了.
(2)由题意:
Up
Ek eU
是电子从无穷远处移到x=0处反抗电场力所做的功
2 ( R2 h2 R12 h2 ) 2 0
f
问以上说法对不对?为什么?
q
2 2
又有人说因为f =qE,E= /0, = q/S,于是作用力为:
40 r
f
q
2
0S
点电荷q 在电场E中所受的力为
适用条件:(1)q为点电荷;
f =qE
(2)此两带电板间的作用力,是一板上电荷的电场 q2 对另一板上电荷的作用力。 E q ; F
E dS
q
i
i内
0
(4)静电场的环路定理
E dr 0
L
(5)电场强度与电势的关系
P
p0
p
E dr
p0 0
(6)电场强度等于电势的负梯度
E ( i j k) x x x
P 0 0
(3)已知场源电荷电势的分布,叠加求较复杂电 荷的电势
5.几种典型带电体的电场强度和电势
(1)点电荷 球对称 E
q 4 0 r r
推广:均匀带电球面;球对称(ρ=ρ(r))带电球体。 (2)无限长均匀带电圆柱面(或直棒) 柱对称 rc ln E外 er ; E内 0 2 0 r 20 r ( p0 0) 推广:无限长均匀带电圆柱体 面对称 (3)无限大均匀带电平面外 E外 2 0 推广:无限长均匀带电平板
基本概念和规律
1 . 基本概念
(1) 电场强度定义 (2) 电通量
(3) 电势
2 . 基本的定律和定理
(1) 库仑定律
p0 We E dl P q0
Φe E dS
S
F E q0
(2) 场强叠加原理 (3) 高斯定理
S
q1 q2 F k 2 er r12
结合下题思考:
2 0 2 0 S
2 0 S
两根无限长的均匀带电直线互相平行,相距为2a, 求每单位长度的带电直线受的作用力?
3.在静电学中,有下面几种常见的场强公式
F E q
E
q 4 0 r
2
V A VB E l
(1)第①式和第②式中的q , 意义是否相同 ? 答:(1)第①式和第②式中的电荷q的意义不同。第① 式中q是置于静电场中并受到电场力F的点电荷;第② 式中电荷q是产生场E的场源电荷。 (2)它们适用的范围怎样? 答:①式普遍适用,它是电场的定义式;②式只适用 于点电荷;③式当A、B两点间距为l时适用于均匀场。
0
r
.
0
p
.
p po
.
ro
由此例看出:当电荷分布扩展到无穷远时 电势零点不能再选在无穷远处。
4.电势零点的选择是完全任意的吗?对无限长带电线或无限 大带电面的电场,可否选在无限远?点电荷的电场,可否选在 电荷上?说明理由并讨论:
如图一个面电荷密度为 的无限大平面,旁边距 离为a的位置有一个点电荷q,点电荷到平面的垂线中 点p的电势Up,有人用叠加原理计算为:
2 2 2 2 U ( R x R x ) (3) p点的场强由: p 2 1 2 0
dU h 1 Ep | x h ( 2 dx 2 0 R2 h2 1 R12 h2 )`
( R2 R1 ) 环心的电势为: U o 2 0 e ( R2 R1 ) U U 0 ( R2 R1 ) Ek 2 0 2 0
3.已知:均匀带电球面,R,Q, 沿半径的均匀带电直线 , 长l0 ,近端距离r0 ,二者电场不影响电荷分布. 求:(1)直线所受电场力; (2)直线的电势能. R O r0
dx
x l0
解:(1)建立坐标轴ox,如图
Ex Q 40 x
2
;
dF E xdq E x dx,
(2)电势能
U Q 40 x
r0 l
F
r0 l
r0
Ql0 dF 40 r0 ( r0 l0 )
;x R
dW Udq Udx
l0 Q ln( 1 ) 40 r0
W
r0 l
r0
dW
Q 40 x
r0
dx
思考:若是x的函数则如何?
q a p , 40 ( a / 2) 2 0 2
是否正确?为什么?
