(完整版)游戏公平练习题
数学游戏比赛的规则公平性试题

数学游戏比赛的规则公平性试题1.小李和小王玩一个游戏,游戏规则是:将分别写有1,2,3,4,5的五张卡片先放在一个盒子里,然后随机抽取2张,把这2张卡片上的数字相加,如果其和为奇数,则小李获胜;如果其和为偶数,则小王获胜.你认为这个游戏公平吗?如果不公平,谁获胜的可能性大?请说明理由.【答案】不公平,小李获胜的可能性大,因为和为奇数的有6种情况,和为偶数的有4种情况【解析】把这些数字分别相加,求出和为偶数和奇数的情况,如果偶数与奇数的次数相同就公平,否则就不公平.解:1+2=3,1+3=4,1+4=5,1+5=6,2+3=5,2+4=6,2+5=7,3+4=7,3+5=8,4+5=9,和为奇数的有6种情况,和为偶数的有4种情况;小李获胜的可能性大.答:不公平,小李获胜的可能性大.点评:先对这些数字两两求和,再根据和的奇偶性来判断.2.一个箱子里有白球2个,黑球1个,红球3个.两个同学玩摸球游戏,规则是这样的:如果摸到白色的球,甲同学得1分;如果摸到红色的球,乙同学得1分;如果摸到黑色的球,则无论是谁摸到,两人均不计分.你认为这个游戏规则公平吗?为什么?如果不公平,你能调整游戏规则吗?【答案】不公平,因为这两种球出现的可能性不相同;红球减少1个,黑球增加1个【解析】白球2个,黑球1个,红球3个,共有6个球,白球占总球数的,红球占总球数的,这两种球出现的可能性不相同,所以这个游戏规则不公平.可以从红球中拿出一个换成黑球,这样各种球的数量相等,出现的可能性相同了,游戏就公平了.解:2+1+3=6(个);2÷6=;3÷6=;<答:这个游戏规则不公平,因为这两种球出现的可能性不相同.红球减少1个,黑球增加1个,游戏就公平了.点评:对于这类题目,判断游戏是否公平的关键是看各种球出现的可能性是否相同,如果可能性相同,则游戏公平,如果可能性不相同,要使游戏公平,就调球的个数即可.3.张强、李远、王军正准备走跳棋,他们利用转盘(如图)确定谁先走,怎样设计这个转盘才算公平呢?【答案】指针指向①②张强赢,指向③④李远赢,指向⑤⑥王军赢【解析】要使游戏公平就要使每个人取胜的可能性都相等,据此设计游戏即可.解:因为将转盘平均分成了6份,所以设计如下:游戏规则:指针指向①②张强赢,指向③④李远赢,指向⑤⑥王军赢.可能性都是:2÷6=可能性相等,则游戏公平.点评:本题关注学生对游戏公平性的理解、规则的描述及可能性的求法,只要给出的规则合理且描述准确即可.用到的知识点为:可能性=所求情况数与总情况数之比.4.请你来判断,下面的游戏规则公平吗?图中的两张牌分别是红桃2和黑桃2.小坤和小宇一起打乒乓球,两人决定抽牌来决定谁先发球.方法是:从中任意抽一张,是红桃2小坤先发球,是黑桃2就让小宇先发球,你认为这样的游戏规则公平吗?【答案】公平【解析】因为只有两张牌,任意抽一张,有2种可能,其中红桃2和黑桃2各一张,可能性各占:1,所以公平,据此解答.解:摸到红桃2和黑桃2的可能性各占:1÷2=,所以游戏规则公平;答:这样的游戏规则公平.点评:本题考查了简单事件发生的可能性的求解,即用可能性=所求情况数÷总情况数或求一个数是另一个数的几分之几用除法计算.5.小王和小李在一个长方形区域内进行抛硬币游戏,如果落到白色区域处算小王赢,落到黑色区域处算小李赢.请在图中画一画,涂一涂,使游戏公平.【答案】【解析】游戏是否公平,关键要看游戏双方获胜的机会是否相等,也就是使硬币落在白色区域和黑色区域的可能性各为,所以把长方形平均分成2份,一份涂成黑色,一份白色即可保证游戏公平.解:因为要使游戏公平,要使硬币落到黑色和白色的可能性为,所以如图所示:.点评:本题考查的是游戏公平性.判断游戏公平性就要计算每个事件的可能性,可能性相等就公平,否则就不公平.用到的知识点为:可能性=所求情况数与总情况数之比.6.在生活中常常用转盘来设计对双方公平的游戏.如图1是4个小朋友设计的转盘.(1)你认为谁设计的转盘能使双方更公平?为什么?(2)如图2是一个转盘,请你将它设计一下,成为一个对双方都公平的转盘游戏并解释游戏规则.【答案】笑笑;转动转盘时,指针指向1时,淘气赢,指向2时,笑笑赢,指向3时,小明赢,指向4时,小丽赢【解析】(1)游戏是否公平,关键要看是否游戏双方赢的机会是否相等,即判断双方取胜的可能性是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等,据此判断即可.(2)要使游戏公平就要使每个人取胜的概率都相等,根据此知识点设计转盘游戏即可.解:(1)笑笑设计的转盘能使双方更公平,因为圆中白色和阴影部分面积各占圆的面积的一半,即可能性都为:3÷6=,可能性相等,所以能使双方公平;(2)如图设计:图2游戏规定:转动转盘时,指针指向1时,淘气赢,指向2时,笑笑赢,指向3时,小明赢,指向4时,小丽赢,他们赢的可能性都为:1÷4=,所以对双方都公平.点评:此题考查对游戏公平性的判断.判断游戏公平性就要计算每个事件的可能性,可能性相等就公平,否则就不公平.用到的知识点为:可能性=所求情况数与总情况数之比.7.请你设计一个翻牌的游戏,要求游戏规则要公平.【答案】用1~8这8张纸牌,打乱反扣在桌上,每次任意翻出一张纸牌,翻到单数算甲赢,翻到双数算乙赢【解析】设计游戏时,只要对他们来说,赢得机会均等就可以了.解:用1~8这8张纸牌,打乱反扣在桌上,每次任意翻出一张纸牌,翻到单数算甲赢,翻到双数算乙赢.点评:题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.8.正方体的六个面分别写着1、2、3、4、5、6,两名同学做游戏,任意抛出正方体后,若朝上的数字是1,甲获胜,若朝上的数字不是1,则乙获胜,你认为这个游戏公平吗?【答案】不公平【解析】看游戏是否公平,主要看双方是否具有均等的机会,如果机会是均等的,那就公平,否则,则不公平.解:这个游戏不公平.因为正方体的每个面分别标有1、2、3、4、5、6这六个数字,其中数字1只有1个,也就是甲胜利的可能性是;不是6的数字有5个,也就是说乙胜利的可能性是,双方的胜利的机会不是均等的,所以说这个游戏不公平;点评:本题考查游戏公平性的判断,判断游戏规则是否公平,就要计算每个参与者取胜的可能性,可能性相等就公平,否则就不公平;用到的知识点为:可能性=所求情况数与总情况数之比.9.两人玩游戏,掷骰子定输赢.骰子的6个面上分别写有1、2、3、4、5、6个数字.(1)请你评判一下,这样的游戏规则公平吗?(2)小芳一定会输吗?(3)请你修改规则,设计一个公平的游戏.【答案】不公平;不一定;如果掷出骰子数字是1、2、3为小林赢,掷出骰子数字是4、5、6为小芳赢【解析】游戏是否公平,关键要看是否游戏双方赢的机会是否相等,即判断双方取胜的概率是否相等.(1)是2的倍数的数有2、4、6,是3的倍数的数有3、6,所以小林赢的可能性是3÷6=,小芳赢的可能性是2÷6=,所以游戏不公平,(2)小芳不一定会输,因为小芳有赢的可能性,(3)如果掷出骰子数字是1、2、3为小林赢,掷出骰子数字是4、5、6为小芳赢,这样游戏就公平了.解:(1)小林赢的可能性是3÷6=,小芳赢的可能性是2÷6=,所以游戏不公平;(2)小芳不一定会输,因为小芳有赢的可能性,(3)如果掷出骰子数字是1、2、3为小林赢,掷出骰子数字是4、5、6为小芳赢,这样游戏就公平了.点评:本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平,概率=所求情况数与总情况数之比.10.桌子上有三张卡片上分别写着3、5、6.如果摆出的三位数是单数,小明就赢,否则小芳就赢(1)这个游戏公平吗?为什么?(2)小芳会赢吗?(3)请你设计一个公平的规则.【答案】不公平,双方的赢机会不均等;不一定;把3张卡片改成4张,其中2张卡片上的数字是单数,2张卡片上的数字是双数【解析】(1)看游戏是否公平,主要看双方是否具有均等的机会,如果机会是均等的,那就公平,否则,则不公平;(2)是否一定会输或会赢,一般要根据概率来判断,具体操作时,也不一定就一定输或一定赢;(3)可以改变已知条件,使游戏对双方获得的机会是均等的就可以了.解:(1)这个游戏不公平.因为用3、5、6能摆出的三位数有:356、365、536、563、653、635共6个,其中有4个是单数,2个是双数,双方的机会不是均等的,所以说这个游戏不公平.(2)从概率的角度来说,小芳赢的可能性小,但不一定就输,也可能赢;(3)可以把3张卡片改成4张,其中2张卡片上的数字是单数,2张卡片上的数字是双数,再按原来的游戏规则就公平了.点评:本题考查游戏公平性的判断,判断游戏规则是否公平,就要计算每个参与者取胜的可能性,可能性相等就公平,否则就不公平;用到的知识点为:可能性=所求情况数与总情况数之比.。
游戏公平练习题

得 封不游戏公平练习题(二)一、冷静思考,正确填写。
1、 掷骰子游戏面朝上的点数出现的结果有(2、掷一枚骰子,点数小于3的有(3、 掷一枚骰子,双数朝上的可能性有()种,每个点数出现的可能性是()种可能,点数于大3的有( )种可能。
)种;如果掷30次,“ 1朝上的次数大约是()。
(填几分之几。
) 旦( )。
4、 把硬币抛向天空,落地后,正面朝上的可能性占 (5、 从一副中国象棋(32枚)中,任意摸出一枚棋子,摸到黑棋的可能性是 ()。
&在一次数学考试中,试卷上有一道选择题,三个选项中只有一个正确,张明实在做不出, 好随意选了一个,那么他答对的可能性是( )。
7、 口袋里有5块红色橡皮,3块黄色橡皮,橡皮的形状、大小相同,从中任意摸一块橡皮,摸 ( )橡皮的可能性大,如果想使两种颜色的橡皮摸到的可能性相等,需要再往袋中放入 ( )橡皮;如果想使摸到黄色橡皮的可能性大,至少要往袋中放入()橡皮( )块。
8、 小平和小玲下军棋,用摸扑克牌来决定由谁先出棋。
他们选了四张扑克牌,其中两张是红桃, 另两张是黑桃。
将四张扑克牌背面朝上,每人摸出一张,如果两人摸出的牌颜色相同, 则小 平先出棋;如果颜色不同则小玲先出棋。
请回答下列问题: ① 摸出两张牌是同样颜色的可能性是几分之几 ?(② 摸出两张牌是不同样颜色的可能性是几分之几 ?(③ 这个游戏规则公平吗?(如图,有A 、B 、C 、D 四个转盘, 9、 ) 小磊和小辉做转盘游戏, 指针停在灰色区域算小磊赢,停 1、2、 3、 4、 5、 6、 1、 2、3、 4、 5、 6、 ① 想让小磊获胜的可能性大,要在( ② 想让小辉获胜的可能性大,要在( ③ 想让两人获胜的可能性均等,可以在 10、小磊和小辉做摸圆片游戏,每次任意摸一个圆片,摸后放回,每人摸 )转盘上玩)转盘上玩 )转盘或(小磊得1分,摸到黑色圆片小辉得1分,摸到灰色圆片小磊和小辉都不得分。
游戏规则的公平性 小学数学 随堂练习

一、选择题1. 骰子上分别有1~6六个数,甲、乙两人玩掷骰子游戏.甲应选择游戏规则()才是公平的.A.掷出的数大于3甲胜,否则乙胜B.掷出的数是3的倍数甲胜,否则乙胜C.掷出数小于3甲胜,否则乙胜2. 聪聪和明明玩摸球游戏(球的大小、材质都相同)。
聪聪摸到白球得1分,明明摸到黑球得1分,摸到其它颜色的球两人都不得分。
每次摸出一个球,记录它的颜色,然后放回去摇匀再摸,每人摸10次,在下面()箱中摸公平。
A.B.C.3. 学校开展运动会,五年级的同学们为了开幕式做了充分的准备。
1.为了服装整齐,五年一班决定购买一套班服,现有A、B两套班服供选择,同学们决定用转动转盘的方式决定,转到红色选A套,转到黄色选B套,转到其他颜色重新转。
下面的四个转盘()是公平的。
A.B.C.D.2.五年二班制作了一张五角星的海报,如下图,每个小方格的面积为1dm2,五角星海报图(阴影部分)的面积约()dm2。
A.26~30 B.19~25 C.9~18 D.4~83.五年三班的陈杰和张皓参加了800米赛跑。
陈杰用了3分钟,获得第一名,张皓比陈杰多跑1分钟。
张皓跑1米平均用了几分钟?下面列式正确的是()。
A.800÷3 B.(3+1)÷800 C.800÷(3+1)D.3÷8004.五年四班用了彩色环做创意花环出场,如图,6个大小相同的铁环连在一起拉直的图形,每个彩色环的长度10cm,铁环粗2cm。
这条锁链的长度是()厘米。
A.60 B.40 C.48 D.504. 小明和小丽做一个游戏,同时扔两枚同样的硬币,下列规则对双方公平的是()A.若两面一样,则小明获胜,两面不一样,则小丽获胜B.如果同时是正面,则小明获胜,其他情况时小丽获胜C.如果同时是正面,则小明获胜,一正一反小丽获胜D.如果同时是反面,则小明获胜,一正一反小丽获胜5. 东东和亮亮下围棋,转动转盘决定谁先走,下面()种方式公平。
游戏公平与不公平-习题精选

游戏公平与不公平习题精选一、基础题1.某校初三(1)班有61名学生,其中男生32名,女生29名,体检时发现男生身高在1.70米以上的有23人,那么任意从这个班中抽取一名同学,是男生且身高在1.70米以上的概率为.2.小红小兰进行摸球游戏.在一个不透明的袋子里装有3个白球,3个黑球和1个红球,游戏规定两个每次可任意从口袋中摸出一个球(不再放回),谁先摸到红球谁获胜,若小红先摸球,她摸到红球的概率为;若小红摸出一球后发现是白球,则小兰继续摸球时,摸到红球的概率为.3.小明和小强进行掷骰子游戏,他们规定同时掷两枚骰子.若出现的点数之和为2的倍数时,小明得1分;若出现点数之和为3或5的倍数时,小强得1分.这个游戏对双方公平吗?如果你认为不公平,如何修改得分规则才能使该游戏对双方公平?4.从一幅扑克牌中任取一张,是梅花的概率为.5.连续掷硬币两次,其中两次结果相同的概率为,两次正面朝上的概率为.6.用图4-3-3两个转盘进行“配紫色”游戏,配成紫色的概率是.7.一个人的生日是周日的概率为,两个人的生日都是星期日的概率为,两个人的生日是一周中同一天的概率为.8.将身高不同的三名同学任意排序,结果恰好是按身高由低到高排的概率为.二、学科内综合题9.若a=3,b=5,则ba=8的概率是多少?三、应用题(9分)10.在一次数学竞赛中的单项选择题规定,选对者得4分,选错者扣1分,不选者不得分也不扣分,每道题都有四个备选答案.假如有一道题你不会做,你是猜一个答案写上去,还是放弃呢?请说明理由.四、创新题(一)教材变型题11.小明和小刚正在玩掷骰子游戏,两人各掷一枚骰子,则两枚骰子的点数之和为奇数的概率为,两枚骰子的点数之积为奇数的概率为.五、中考题12.(2004,河北课改实验区,8分)依据闯关游戏规则,请你探索闯关游戏的奥秘:(1)用列表的方法表示所有可能的闯关情况;(2)求出闯关成功的概率.闯关游戏规则图4-3-4所示的面板上,有左右两组开关按钮,每组中的两个按钮均分别控制一个灯泡和一个发音装置.同时按下两组中各一个按钮:当两个灯泡都亮时闯关成功;当按错一个按钮时,发音装置就会发出“闯关失败”的声音.13.(2003,威海,3分)某市民政部门今年元宵节期间举行了“即开式社会福利彩票”销售活动,设置彩票3000万张(每张彩票2元).在这些彩票中,设置了如下奖项:资金(万元)501584……数量(个)202020180……如果花2元钱购买1张彩票,那么能得到8万元以上(包括8万元)大奖的概率是.加试题:竞赛趣味题(10分)李勇的爸爸出差回来,向他讲了这样一件事情,在一个地方有一种“摸彩”活动.一个人手提一个袋子,身边立着一块牌子,边指边说:“我这口袋里有10个红球10个白球,哪位愿意来摸球做游戏,一次交10元,但不白交.请你不要看,从口袋里摸出10个球,按牌子上的结果安排:10个都是红球退还10元外再送你10元线;9个红球1个白球退还10元外再送你8元;8个红球2个白球退还10元外再送你6元;7个红球3个白球退还10元外再送你4元;6个红球4个白球退还10元不再送了;5个红球5个白球算你运气不好,不退还了;4个红球6个白球退还10元不再送了;3个红球7个白球退还10元外再送你4元;2个红球8个白球退还10元外再送你6元;1个红球9个白球退还10元外再送你8元;10个都是白球退还10元外再送你10元.共十一种可能,八种可能让你赢钱,只有一种可能输,这么便宜的事,谁来试试啊?李勇的爸爸亲眼看见有几个青年人掏钱试了试,结果都输了,且谁摸的次数越多,谁就输得越多.爸爸让李勇利用所学的概率统计知识计算一下,这是为什么?请你也计算一下,找出其中的原因.参考答案 一、1.6123点拨:不要让数字混淆概念,把握问题:身高在1.7米以上的男生只有23人,其概率一定为6123.2.61;71 点拨:小红摸到白球后,不再放回,则袋中还有2个白球;3个黑球,1个红球,因而小兰再摸到红球的概率为61.3.解:游戏不公平,出现点数之和为2的倍数的概率为21,出现点数之和为3或5的倍数的概率为36193673612=+,因而游戏不公平.可以将得分规则改为若出现点数之和为2倍数时,小明得19分,若出现点数之和为3或5的倍数时,小强得18分.点拨:由列表得出结果进行正确的判断即可.4.54136.61 解:由列表结果可知共有12个结果,其中紫色为2个,即61122=. 7.71;491;71 解:由列表结果可知两个人的生日都是星期日的概率为491,即共有49个结果,两个人生日为同一天有7个结果,因而概率为71497=.点拨:也是一个由列表法可以求解概率的简单事件.8.61解:三个人的大小个为1,2,3,则分析其可能的排序结果为:123,132,213,231,312,321,且每一个结果的可能性是相等的,因而排序恰好按身高由低到高的概率为61.点拨:不是一个可以用列表、或树状图可求概率的简单事件,需要合情推理出其所有可能出现的错误,从而计算其概率.二、9.解:由|a|=3,∴a=±3,|b|=5.∴b=±5.由列表的结果可知,a +b 的结果为8,2,-2,-8,则b a +=8的概率为21.点拨:列表计算概率是常用的方法.三、10.解:放弃得分为0分;若猜一个答案的平均得分为4×41+(-1)×43=41(分),即猜一个答案的平均得分为0.25分,所以猜一个答案还是值得的.四、(一)11.21;41五、12.解:(1)所有可能闯关情况列表如下:(2)设两个1号按钮控制一个灯泡,P (闯关成功)=41.13.2×10-6加试题:解:现在让我们计算一下十一种情况每一种发生的概率是多少. 20个球中摸10个球的不同方法的种数为:C 1020=1234567891011121314151617181920⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯=184756.摸10个球都是红球只有一种,即C 1010C 010=1,概率为1847561=0.0000054.摸10个球9个红球1个白球的不同方法的种数为C 910C 110=100,概率为184756100=0.00054.计算方法都相同,十一种情况的概率分别为:可见摸球者输钱的概率为0.344,赢钱的概率为:2×(0.0000054+0.00054+0.011+0.078)=0.1790908.赢钱中得10元的可能性几乎是0,最大可能是4元,而输钱则一下输10元,这就是摸的次数越多输得越多的原因.。
游戏公平吗练习3

1.游戏公平吗
上面是一副扑克牌的两组牌,红桃8张,草花8张,按以上排列顺序不变,背面朝上,请小红、小明闭上眼睛做下面的游戏.
1.把1组扑克按顺序摞好请小红任意拿2张相邻的扑克,2张扑克的数相加为奇数得分,否则不得分.
2.同理,把2组扑克按顺序叠好,请小明来抽取2张相邻扑克,2张扑克的数相加为奇数得分,否则不得分.
扑克牌的顺序始终不变,共抽取10次,记录得分情况.
次 1 2 3 4 5 6 7 8 9 10
小红
小明
这次游戏对小红、小明公平吗?说说你的理由.
参考答案
1.游戏公平吗
不公平理由略。
五年级上册数学练习- 游戏规则的公平性 冀教版

游戏规则的公平性(练习)一、填空题。
1、口袋中有红球3个,蓝球3个,黄球1个,任意摸一个球,摸到()球的可能性最小,摸到()球和()球的可能性相等。
2、一副扑克牌,从中任意抽出一张,是红桃的可能性和是黑桃的可能性()。
3、袋子里有大小一样的红球和黄球各8个,要使摸到红球的可能性大,袋子里至少要再放入()个红球。
4、有5张数字卡片(如下图),倒扣着混放在一起,每次反过来1张,记下数字后再放回去和其他卡片混合。
(1)每次翻开的数字有()种可能。
(2)如果翻开的数字大于5,翻开的卡片有()种可能,可能是()。
(3)翻开的数字卡片大于5和小于5的可能性()。
二、判断题。
1、从一副扑克牌中任抽一张,抽到红桃6的可能性与抽到黑桃10的可能性相等。
()2、盒内放着5个红球和5个黄球(除颜色外,其余都相同),从中任意摸一个球,摸到红球和黄球的可能性相同。
()3、一个正方体的每个面上分别标有数字1、2、3、4、5、6,甲乙两人轮流掷正方体,若朝上的数字是6,则甲获胜,如朝上的数字不是6,则乙获胜,甲获胜的可能性大。
()4、两个小朋友玩游戏,掷骰子决定输赢。
小芳说:“朝上的一面是2的倍数我赢。
”小雨说:“是3的倍数我赢。
”这个游戏规则是公平的。
()三、选择题。
1、在一副洗好的扑克牌中随意抽取一张,抽到“小王”的可能性与抽到“红桃9”的可能性相比,()。
A、抽到“小王”的可能性大B、抽到“红桃9”的可能性大C、抽到“小王”与“红桃9”的可能性相等D、无法确定2、如图,转盘转到()区域的可能性最小。
A、黄色B、红色C、绿色D、蓝色3、甲乙两人做游戏,同时掷两枚相同的硬币,双方约定:同面朝上甲胜,异面朝上则乙胜,则这个游戏()。
A、对双方公平B、对甲有利C、对乙有利D、无法确定4、小静和小红玩掷骰子游戏,每人将一个各面分别标有数字1、2、3、4、5、6的正方体骰子掷一次,把两人掷得的点数相加,并约定:若点数之和等于6,则小静赢;若点数之和等于7,则小红赢;若点数之和是其他数,则两人不分胜负,那么()。
游戏公平性-初中数学习题集含答案

游戏公平性(北京习题集)(教师版)一.填空题(共1小题)1.(2013秋•通州区校级月考)一个箱子中放有红、黄、黑三种小球,三个人先后去摸球,一人摸一次,一次摸出一个小球,摸出后放回,摸出黑色小球为赢,这个游戏是 的.(填“公平”或“不公平”二.解答题(共5小题)2.(2019秋•房山区期末)现有,两个不透明的袋子,分别装有3个除颜色外完全相同的小球,其中袋中装有2个白球,1个红球;袋中装有2个红球,1个白球.小林和小华商定了一个游戏规则:从摇匀后的,两袋中各随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜.请用列表法或画树状图法,说明这个游戏对双方是否公平.3.(2019秋•海淀区期末)一个不透明的布袋中有完全相同的三个小球,把它们分别标号为1,2,3.小林和小华做一个游戏,按照以下方式抽取小球:先从布袋中随机抽取一个小球,记下标号后放回布袋中搅匀,再从布袋中随机抽取一个小球,记下标号.若两次抽取的小球标号之和为奇数,小林赢;若标号之和为偶数,则小华赢.(1)用画树状图或列表的方法,列出前后两次取出小球上所标数字的所有可能情况;(2)请判断这个游戏是否公平,并说明理由.4.(2019秋•西城区校级期中)甲、乙两人进行摸牌游戏.现有十张形状大小完全相同的牌,正面分别标有数字.从中选出一些牌,将这些牌背面朝上,洗匀后放在桌子上.甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.若两人抽取的数字和为2的倍数,则甲获胜;其余情况,乙获胜.(1)若选出三张分别标有数字2、3、5的牌,这个游戏公平吗?请利用树状图或列表法来解释说明.(2)乙说:“若我在2、3、5三张牌外再选一张牌,共四张牌进行游戏,则我可以让自己获胜的可能性比甲大”,请判断乙的说法是否正确,若正确,请写出乙可以再选哪些牌让自己获胜的可能性比甲大;若不正确,请说明理由.5.(2017秋•石景山区期末)小红和小丁玩纸牌游戏:如图是同一副扑克中的4张牌的正面,将它们正面朝下洗匀后放在桌上,小红先从中抽出一张,小丁从剩余的3张牌中也抽出一张.比较两人抽出的牌面上的数字,数字大者获胜.(1)请用树状图或列表法表示出两人抽牌可能出现的所有结果;(2)这个游戏公平吗?请说明理由.6.(2017春•海淀区校级月考)甲、 乙两人进行摸牌游戏 . 现有四张形状大上完全相同的牌, 正面分别标有数字 1 , 2 , 3 , 4 . 将四张牌背面朝上, 洗匀后放在桌子上 .甲从中随机抽)A B A B A B 1~10取一张牌,记录数字后放回洗匀,乙再随机抽取一张.(1)请用列表法或画树状图的方法,求两人抽取相同数字的概率.(2)若两人抽取的数字差的绝对值等于 1 ,则甲获取;若抽取的数字差的绝对值大于 1 ,则乙获胜,这个游戏公平吗?请用概率的知识加以解释.游戏公平性(北京习题集)(教师版)参考答案与试题解析一.填空题(共1小题)1.(2013秋•通州区校级月考)一个箱子中放有红、黄、黑三种小球,三个人先后去摸球,一人摸一次,一次摸出一个小球,摸出后放回,摸出黑色小球为赢,这个游戏是 公平 的.(填“公平”或“不公平”【分析】根据题意可得:三个人先后去摸球,一人摸一次,而且摸出后放回,故摸出黑色小球的概率相等;故这个游戏公平.【解答】解:每个人摸到黑球的概率均为,所以游戏公平. 【点评】本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个参与者取胜的概率,概率相等就公平,否则就不公平.用到的知识点为:概率所求情况数与总情况数之比.二.解答题(共5小题)2.(2019秋•房山区期末)现有,两个不透明的袋子,分别装有3个除颜色外完全相同的小球,其中袋中装有2个白球,1个红球;袋中装有2个红球,1个白球.小林和小华商定了一个游戏规则:从摇匀后的,两袋中各随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜.请用列表法或画树状图法,说明这个游戏对双方是否公平.【分析】根据题意列出图表得出所有等可能的结果数和颜色相同和不同的结果数,然后根据概率公式求出各自的概率,再进行比较即可得出这个游戏是否公平. 【解答】解:列表如下:红 红 白 白(白,红 (白,红 (白,白) 白(白,红 (白,红 (白,白) 红 (红,红 (红,红 (红,白)由上表或可知,一共有9种等可能的结果,其中颜色相同的结果有4种,颜色不同的结果有5种.(颜色相同),(颜色不同). , 这个游戏规则对双方不公平.【点评】本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个参与者取胜的概率,概率相等就公平,否)13=A B A B A B AB 12111)12)1221)22)21)2)P ∴49=P 59=Q 4599<∴则就不公平.用到的知识点为:概率所求情况数与总情况数之比.3.(2019秋•海淀区期末)一个不透明的布袋中有完全相同的三个小球,把它们分别标号为1,2,3.小林和小华做一个游戏,按照以下方式抽取小球:先从布袋中随机抽取一个小球,记下标号后放回布袋中搅匀,再从布袋中随机抽取一个小球,记下标号.若两次抽取的小球标号之和为奇数,小林赢;若标号之和为偶数,则小华赢.(1)用画树状图或列表的方法,列出前后两次取出小球上所标数字的所有可能情况;(2)请判断这个游戏是否公平,并说明理由.【分析】(1)根据题意画出树状图得出所有等情况数即可;(2)根据概率公式先求出标号之和为奇数和偶数的概率,再进行比较,即可得出这个游戏是否公平.【解答】解:(1)由题意画出树状图如下:所有可能情况如下:,,,,,,,,.(2)由(1)可得:标号之和分别为2,3,4,3,4,5,4,5,6,标号之和为奇数的概率是:, 标号之和为偶数的概率是:, 因为, 所以不公平.【点评】本题考查的是用列表法或画树状图法求概率.用到的知识点为:概率所求情况数与总情况数之比.4.(2019秋•西城区校级期中)甲、乙两人进行摸牌游戏.现有十张形状大小完全相同的牌,正面分别标有数字.从中选出一些牌,将这些牌背面朝上,洗匀后放在桌子上.甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.若两人抽取的数字和为2的倍数,则甲获胜;其余情况,乙获胜.(1)若选出三张分别标有数字2、3、5的牌,这个游戏公平吗?请利用树状图或列表法来解释说明.(2)乙说:“若我在2、3、5三张牌外再选一张牌,共四张牌进行游戏,则我可以让自己获胜的可能性比甲大”,请判断乙的说法是否正确,若正确,请写出乙可以再选哪些牌让自己获胜的可能性比甲大;若不正确,请说明理由.【分析】(1)根据题意画出树状图得出所有等情况数和两人抽取的数字和为2的倍数的情况数,再根据概率公式求出甲和乙的概率,然后进行比较,即可得出答案;=(1,1)(1,2)(1,3)(2,1)(2,2)(2,3)(3,1)(3,2)(3,3)49594599≠=1~10(2)分两种情况讨论,当另选的一张牌是奇数时,求出甲获胜的概率,当另选的一张牌是偶数时,求出甲获胜的概率,从而得出乙的说法是否正确.【解答】解:(1)所有可能出现的结果如图:从图中看出,总共有9种结果,每种结果出现的可能性相同,其中两人抽取的数字和为2的倍数的有5种,所以甲获胜的概率为,乙获胜的概率是, 则不这个游戏公平;(2)当选择的牌是奇数时,, 当选择的牌是偶数时,, 因此,乙不可以让自己获胜的可能性比甲大.【点评】本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率所求情况数与总情况数之比.5.(2017秋•石景山区期末)小红和小丁玩纸牌游戏:如图是同一副扑克中的4张牌的正面,将它们正面朝下洗匀后放在桌上,小红先从中抽出一张,小丁从剩余的3张牌中也抽出一张.比较两人抽出的牌面上的数字,数字大者获胜.(1)请用树状图或列表法表示出两人抽牌可能出现的所有结果;(2)这个游戏公平吗?请说明理由.【分析】(1)根据题意画出树状图,即可解决问题;(2)根据树状图,利用概率公式即可求得小红获胜的概率,由概率相等,即可判定这个游戏公平;【解答】解:(1)树状图如右:5949()58p =甲获胜()12p =甲获胜=则小红获胜的概率:,小丁获胜的概率:, 所以这个游戏比较公平.【点评】本题考查的是用列表法与树状图法求事件的概率,解题的关键是学会正确画出树状图,判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率所求情况数与总情况数之比..6.(2017春•海淀区校级月考)甲、 乙两人进行摸牌游戏 . 现有四张形状大上完全相同的牌, 正面分别标有数字 1 , 2 , 3 , 4 . 将四张牌背面朝上, 洗匀后放在桌子上 . 甲从中随机抽取一张牌, 记录数字后放回洗匀, 乙再随机抽取一张 .(1) 请用列表法或画树状图的方法, 求两人抽取相同数字的概率 .(2) 若两人抽取的数字差的绝对值等于 1 ,则甲获取;若抽取的数字差的绝对值大于 1 ,则乙获胜, 这个游戏公平吗?请用概率的知识加以解释 .【分析】(1) 观察已知树状图得出所有等可能的情况数, 进而找出抽取数字相同的情况数, 即可求出所求概率;(2) 求出甲乙两人获胜的概率, 比较即可作出判断 .【解答】解: (1) 根据题意得:; (2) 若两人抽取的数字差绝对值等于 1 ,,甲胜, 若绝对值大于 1 ,,乙胜, , 不公平 .【点评】此题考查了游戏公平性, 以及列表法与树状图法, 弄清概率的求法是解本题的关键 .61122=61122==41164P ==63168P ==716P =Q 671616<∴。
游戏的公平与不公平习题(B卷)
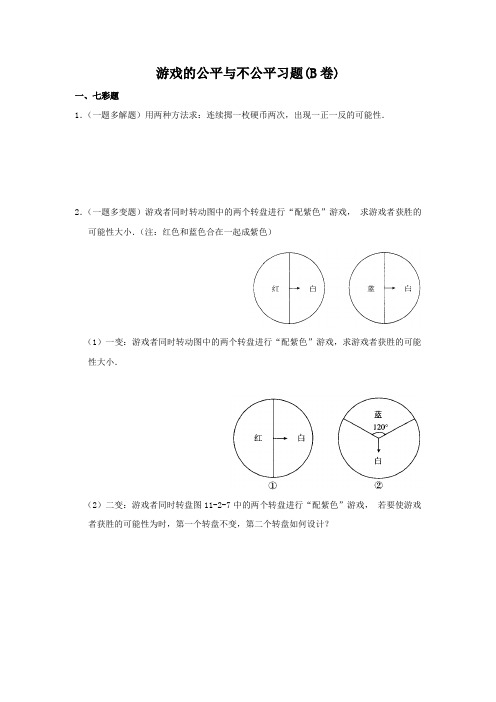
游戏的公平与不公平习题(B卷)一、七彩题1.(一题多解题)用两种方法求:连续掷一枚硬币两次,出现一正一反的可能性.2.(一题多变题)游戏者同时转动图中的两个转盘进行“配紫色”游戏,•求游戏者获胜的可能性大小.(注:红色和蓝色合在一起成紫色)(1)一变:游戏者同时转动图中的两个转盘进行“配紫色”游戏,求游戏者获胜的可能性大小.(2)二变:游戏者同时转盘图11-2-7中的两个转盘进行“配紫色”游戏,•若要使游戏者获胜的可能性为时,第一个转盘不变,第二个转盘如何设计?二、知识交叉题3.(当堂交叉题)张彬和王华两位同学为得到一张观看足球比赛的入场券,各自设计了一种方案:张彬:如图,设计了一个可以自由转动的转盘,随意转动转盘,转动停止后,当指针指向阴影区域时,张彬得到入场券;否则,王华得到入场券;王华:将三个完全相同的小球分别标上数字1,2,3后,放入一个不透明的袋子中.摇匀后,从中随机取出一个小球,记下小球上的数,然后放回袋子;混合均匀后,再随机取出一个小球,记下小球上的数.若两次取出的小球上的数字之和为偶数,•王华得到入场券;否则,张彬得到入场券.请你运用所学的知识,分析张彬和王华的设计方案对双方是否公平.4.(科内交叉题)某公司现有甲、乙两种品牌的打印机.其中甲品牌的有A,B两种型号,乙品牌的有C,D,E三种型号.朝阳中学计划从甲、•乙两种品牌中各选购一种型号的打印机.(1)写出所有选购方案;(2)若各种型号的打印机被选购的可能性相同,那么C•型号的打印机被选购的可能性是多少?(3)各种型号的打印机的价格如下表:甲品牌乙品牌型号 A B C D E价格(元)2000 1700 1300 1200 1000朝阳中学购买了两种品牌的打印机共30台,其中乙品牌的选购了E型号,•共用去资金5万元,问E型号的打印机购买了多少台?三、实际应用题5.将A,B,C,D四人随机分成甲,乙两组参加羽毛球比赛,每组两人,列出所有可能出现的结果.(1)A在甲组的可能性是多少?(2)A,B都在甲组的可能性是多少?四、经典中考题6.(2008,南宁,2分)在一个不透明的摇奖箱内装有20个形状,大小,•质地等完全相同的小球,其中只有5个球标有中奖标志,•那么随机抽取一个小球中奖的可能性是_______.7.(2008,北京(有改动),4分)如图,有5张形状、大小、•质地均相同的卡片,正面分别印有北京奥运会的会徽,吉祥物(福娃),火炬和奖牌等四种不同的图案,背面完全相同.现将这5张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,•抽出的卡片正面图案恰好是吉祥物(福娃)的可能性是()A.15B.25C.12D.358.(2008,天津(有改动),3分)掷两枚质地均匀的硬币,则两枚硬币全部正面朝上的可能性等于()A.1 B.12C.14D.0五、探究学习1.(结论开放题)甲、乙两同学设计了这样一个游戏:把三个完全一样的小球分别标上数字1,2,3后,放在一个不透明的口袋里,甲同学先随意摸出一个球,•记住球上标注的数字,然后记乙同学抛掷一枚质地均匀的、各面分别标有数字1,2,3,4,5,6的正方体骰子,记住掷得的点数,又得到另一个数字,再把两个数字相加.若两人的数字之和小于7,则甲获胜;否则,乙获胜.(1)请把两人所得的数字之和的所有结果都列举出来;(2)这个游戏对双方公平吗?如果公平,请说明理由;如果不公平,•请你加以改进,使游戏变得公平.2.阅读以下材料,并解答以下问题.“完成一件事有两类不同的方案,在第一类方案中有m (种)不同的方法.在第二类方案中有n种不同的方法,这是分类加法计数原理;完成一件事需要两个步骤,做第一步有m种不同的方法,做第二步有n种不贩方法,那么完成这件事共有N=mn(种)不同的方法,这就是分步乘法的计数原理.”如完成沿图1所示的街道从A点出发向B•点行进这件事(规定必须向北走或向东走),会有多少种不同的走法,其中从A•点出发到某些交叉点的走法数已在图2中填出.图1 图2(1)根据以上原理和图2的提示,算出从A点出发到达其余交叉点的走法数,将数填入图2的空圆中,并回答从A点出发到B点的走法共有多少种?(2)运用适当的原理和方法算出从A点出发到达B点,并禁止通过交叉点C•的走法有多少种?(3)现由于交叉点C道路施工,禁止通行,求如任选一种走法,从A点出发能顺利开开到达B点(无返回)的可能性是多少?3.(统计方案设计题)设计一个两步摸球游戏,使两次摸到红球的可能性为38.四、说理题4.在一个不透明的盒子中装着分别标有数字1,2,3,4的四个完全相同的小球.•现在甲、乙两位同学做游戏,游戏规则是:“甲先从盒子中随机摸出一个小球,记下小球的数字后放回,摇匀后,乙再从盒子中随机摸出一个小球,也记下小球的数字后放回,则游戏结束,若记下的数字甲比乙大,则甲获胜;若记下的数字甲不比乙大,则乙获胜”.(1)请你分析此游戏可能出现的结果有多少种;(2)该游戏对甲、乙双方公平吗?说明理由.参考答案一、1.分析:求某事件发生可能性的方法有两种:一是树状图法,二是列表法.解法一:画树状图,如答图11-2-1所示:由树状图可知共有4种可能,出现“一正一反”的可能性是24=12.解法二:列表:正反正(正,正)(正,反)反(反,正)(反,反)由上表可知共有4种可能,出现“一正一反”的可能性为24=12.点拨:无论用哪种方法求解,要做到不重不漏,即要把所有可能的情况列出来.2.分析:根据转盘各颜色区域的大小,列出所有可能出现的情况,•再找红色和蓝色在一起的数目.解:列表:红白蓝(蓝,红)(蓝,白)白(白,红)(白,白)所以,游戏者获胜的可能性为4.(1)把题图②中的白色区域平分为两部分,记为白1,白2,列表:红白蓝(蓝,红)(蓝,白)白1 (白1,红)(白1,白)白2 (白2,红)(白2,白)所以,游戏者获胜的可能性为16.(2)如图所示(提供一种).点拨:红色加上蓝色是紫色,图中的白色区域可以平均分成四份,•每份和蓝色区域大小是相同的.二、3.分析:要分析设计方案对双方是否公平,需求出每种方案双方获胜的可能性大小.解:张彬的设计方案:张彬得到入场券的可能性为[360-(100+70)÷360=1936,王华得到入场券的可能性为(100+70)÷360=1736,因为1936>1736,所以张彬的设计方案对双方不公平.王华的设计方案:可能出现的所有结果列表如下:1 2 31 2 3 42 3 4 53 4 5 6所以王华得到入场券(即和为偶数)的可能性为59,张彬得到入场券(即和不为偶数)的可能性为49,因为59>49,所以王华的设计方案对双方也不公平.点拨:双方获胜的可能性若相等,则游戏对双方是公平的;若不相等,则是不公平的.4.分析:先列出所有选购方案,再求C型号打印机被选购的可能性的大小.解:(1)所有选购方案为:(A,C),(A,D),(A,E),(B,C),(B,D),(B,E)(•括号中前一个表示从甲品牌中选购的,后一个表示从乙品牌中选购的),共6种情况.(2)由(1)知C型号的打印机被选购的可能性大小为26=13.(3)设选购E型号的打印机x台(x为正整数),则选购甲品牌(A或B型号)的(30-x)•台,由题意,得当甲品牌选A型号时,1000x+(30-x)×2000=50000,解得x=10.当甲品牌选B型号时,1000x+(30-x)×1700=50000,解得x=107(不合题意),故E型号的打印机应选购10台.点拨:本题综合考查了列方程解应用题及确定随机事件的可能性等知识.三、5.分析:将A,B,C,D四人随机分成甲,乙两组所有可能出现的结果列出,再求解.解:所有可能出现的结果如下:总共有6种结果,每种结果出现的可能性相同.(1)所有的结果中,满足A在甲组的结果有3种,所以A在甲组的可能性为36=12.(2)所有的结果中,满足A,B都在甲组的结果只有1种,所以A,B都在甲组的可能性为16.点拨:用列表法列出所有分组的结果比较简便.四、6.14点拨:520=14.7.B 点拨:因为5张卡片中,印有吉祥物的卡片只有两张,因此抽出卡片正面图案恰好是吉祥物(福娃)的可能性为,故选B.8.C 点拨:可能出现的结果为:正正,正反,反正,反反,•所以全部正面朝上的可能性为14.五、探究学习1.分析:先用适当的方法将两人所得的数字之和的所有结果列举出来,再分别计算数字之和小于7,等于大于7的可能性,最后判断出游戏的公平性.解:(1)如图所示.(2)甲获胜的可能性为1218=23,乙获胜的可能性为618=13,所以这个游戏对双方不公平.公平的游戏规则为:若两人所得的数字之和小于6,则甲获胜;否则,乙获胜.理由如下:•两人所得的数字之和小于6的可能性为918=12;数字之和大于且等于6的可能性也为,甲组乙组AB CDAC BDAD BCBC ADBD ACCD AB所以对于双方是公平的12.点拨:(1)也可用列法表;(2)答案不唯一,只要符合要求即可.2.分析:通过阅读,弄懂题意是解答的关键.解:(1)因为完成从A点到达B点必须向北走或向东走,所以到达A点以外的任意交叉点的走法数只能是与其相邻的南边的交叉点和西边的交叉点的数之和,•故使用分类加法计数原理,由此算出从A点到达其余各交叉点的走法数,填表如图1.图1 图2故从A点出发到B点的走法共有35种.(2)方法一:可先求从A点到B点,并经过交叉点C的走法数,再用从A点到B•点总的走法数减去它,即得从A点到B点,但不经过交叉点C的走法数.完成从A点出发经C 点到B点这件事可分两步,先从A点到C点,再从C点到B点,使用分步乘法计数原理,算出从A点到C点的走法有3种,见图2;算出从C点到B点的走法为6种,见图3,•再动用分步乘法计数原理,得到从A点经C点到B点的走法有3×6=18(种),所以从A•点到B点不经过C点的走法有35-18=17(种).图3 图4方法二:交叉点C可视为相邻道路不通,可删除与C点相连的线段,从A点到各交叉点的走法数见图4.所以从A点到B点并禁止经过C点的走法有17种.(3)从A点出发能顺利开车到达B点的可能性为17 35.3.解:在不透明袋甲中放入1个红球,1个黑球,不透明袋乙中放入3个红球,1个黑球,这些球除颜色外其余都相同,分别从甲,乙两袋中各摸出一球,两次都摸到红球的可能性为12×34=38.点拨:本题的设计方案是开放的,只要符合题意即可.4.分析:明确游戏规则是解答的关键.解:(1)这个游戏可能出现的结果共有16种(括号中前一个表示甲,后一个表示乙),即(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4).(2)该游戏对甲,乙双方不公平,理由如下:因为记下的数字甲比乙大的有6种情况,分别是(2,1),(3,1),(3,2),(4,1),(4,2),(4,3).所以甲获胜的可能性为6÷16=38,乙获胜的可能性为(16-6)÷16=58,•所以该游戏对甲,乙双方不公平.点拨:先求出甲、乙分别获胜的可能性,再比较其大小,最后判断是否公平.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
密 封 线 学校
班级 姓名 学号
密 封 线 内 不 得 答 题
游戏公平练习题(二)
一、冷静思考,正确填写。
1、掷骰子游戏面朝上的点数出现的结果有( )种,每个点数出现的可能性是( )。
2、掷一枚骰子,点数小于3的有( )种可能,点数于大3的有( )种可能。
3、掷一枚骰子,双数朝上的可能性有( )种;如果掷30次,“1”朝上的次数大约是( )。
4、把硬币抛向天空,落地后,正面朝上的可能性占( )。
( 填几分之几。
)
5、从一副中国象棋(32枚)中,任意摸出一枚棋子,摸到黑棋的可能性是( )。
6、在一次数学考试中,试卷上有一道选择题,三个选项中只有一个正确,张明实在做不出,只
好随意选了一个,那么他答对的可能性是( )。
7、口袋里有5块红色橡皮,3块黄色橡皮,橡皮的形状、大小相同,从中任意摸一块橡皮,摸
( )橡皮的可能性大,如果想使两种颜色的橡皮摸到的可能性相等,需要再往袋中放入( )橡皮;如果想使摸到黄色橡皮的可能性大,至少要往袋中放入( )橡皮( )块。
8、小平和小玲下军棋,用摸扑克牌来决定由谁先出棋。
他们选了四张扑克牌,其中两张是红桃,
另两张是黑桃。
将四张扑克牌背面朝上,每人摸出一张,如果两人摸出的牌颜色相同,则小平先出棋;如果颜色不同则小玲先出棋。
请回答下列问题: ①摸出两张牌是同样颜色的可能性是几分之几? ( ) ②摸出两张牌是不同样颜色的可能性是几分之几? ( ) ③这个游戏规则公平吗? ( )
9、如图,有A 、B 、C 、D 四个转盘,小磊和小辉做转盘游戏,指针停在灰色区域算小磊赢,停
在白色区域算小辉赢。
A B C D ①想让小磊获胜的可能性大,要在( )转盘上玩。
②想让小辉获胜的可能性大,要在( )转盘上玩。
③想让两人获胜的可能性均等,可以在( )转盘或( )转盘上玩。
10、小磊和小辉做摸圆片游戏,每次任意摸一个圆片,摸后放回,每人摸30次,摸到白色圆片
小磊得1分,摸到黑色圆片小辉得1分,摸到灰色圆片小磊和小辉都不得分。
下面有A 、B 、C 三个口袋,在( )袋中摸圆片小磊获胜可能性大,在( )袋中摸圆片小辉获胜可能性大,在( )袋中摸圆片两人获胜机会相等。
A B C
11、小磊和小辉做摸圆片游戏,每次任意摸一个圆片,摸后放回,每人摸30次。
摸到白色圆片
小磊得1分,摸到黑色圆片小辉得1分,摸到灰色圆片小磊和小辉都不得分。
下面有A 、B 、C 三个口袋,在( )袋中摸圆片小磊获胜可能性大,在( )袋中摸圆片小磊获胜可能性大,在( )袋中摸圆片两人获胜机会相等。
二、仔细推敲,判断正误。
(对的在括号里打“√”,错的打“×” ) 1、两位同学采用“石头、剪刀、布”的方法决定谁先跳房子,这个游戏方法是不公平的。
( ) 2、球赛中,用抛硬币的方法决定谁先开球是公平的。
……………………………………( ) 3、1~9,9张数字卡片,抽到单数的可能性和抽到双数的可能性一样大。
…………….( ) 4、掷一种正方体的骰子(各面分别写着1,2,3,4,5,6)掷出6的可能性大一些。
( ) 5、.袋里装的全是红球,淘气摸球时可能摸到白球。
……………………………………..( ) 6、掷一枚骰子,点数小于3有3种可能。
………………………………………………..( ) 三、认真分辨,正确选择。
(把正确答案的序号填在括号里。
)
1、笑笑从右面的盒子中任意摸出一个球,摸到( )球的可能性最大,摸到( ) 球的可能性最小。
A 、白球
B 、黄球
C 、红球
2、抛一枚硬币,落下后正面朝上与反面朝上的可能性相比,( )。
A 、正面朝上的可能性大。
B 、反面朝上的可能性大。
C 、可能性一样大。
3、学校食堂里有3种荤菜,有2种素菜,一份盒饭含有一个荤菜和一个素菜,小明吃一份盒饭,有( )种配菜方法。
A 、2
B 、3
C 、5
D 、6
4、甲、乙两人用“石头、剪子、布……”作为游戏规则,玩摸球游戏,这样玩的结果( )。
A 、甲胜多一些 B 、乙胜多一些 C 、一样公平(两个胜算差不多) D 、无法确定
5、扑克牌有四种不同的花色。
现有红桃3,黑桃3,红桃3,方片6,梅花6,共5张扑克牌,倒扣在桌面上。
如果只抽一次,抽到红桃3的可能性是( )。
A 、3
1
B 、41
C 、52
D 、61
6、一个正方体的每个面上分别标有数字1,2,3,4,5,6。
甲、乙两人任意掷出正方体后,若朝上的数字是6,则甲获胜;若朝上的数字不是6,则乙获胜。
( )获胜的可能性大。
A 、甲 B 、乙 四、操作题。
1、李明、张兵和陈华三人玩转盘游戏,指针停在白色区域算李明胜,指针停在黑色区域算张兵胜,指针停在红色区域算陈华胜。
(10分)
① ② ③ ④
(1)李明想让自己胜的可能性大,会选( )号转盘。
(2)要想他们三人都公平,应选用( )号转盘做游戏,。
(3)选①号转盘,( )胜的可能性大。
(4)选( )号转盘,李明和张兵输的可能性一样大。
(5)陈华要想胜率大一些,必须选( )号转盘。
密 封 线 内 不 得 答 题
2、在每个圆盘上按要求涂色。
转到红色的可能性大, 转到黄色的可能性大, 转到红色和黄色 转到黄色的可能性小。
转到红色的可能性小。
的可能性同样大。
3、请你动手设计一个转盘使指针停在红色区域的可能性为52,指针停在黄色区域的可能性为5
1
.
四、解决问题。
1.如右图,转盘上分别涂有4种颜色。
(1)指针停在红色区域的可能性是多少?
(2)如果转盘转动100次,估计大约会有多少次指针是停在黄色区呢?
2、这是笑笑设计的转盘。
请你为她确定游戏规则,使游戏对双方都公平。
3、桌子上摆着1~20这20张数字卡片。
如果摸到一位数淘气赢,如果摸到两位数,笑笑赢。
(1)这个游戏公平吗?
(2)笑笑一定能赢吗?
(3)你能设计一个公平的游戏规则吗?试试看。
4、一个小正方体,在6个面上分别写上数字,甲、乙两人各抛20次。
你觉得下面哪些游戏规
则是公平的?为什么? (1)三个面写“1”,三个面写“2”。
“1”朝上甲赢,“2”朝上乙赢。
(2)四个面写“2”,两个面写“4”。
“2”朝上甲赢,“4”朝上乙赢。
(3)六个面分别写1~6这6个数字,朝上的数小于或等于3甲赢,大于3则乙赢。
5、在一个正方体的6个面上分别标上数字,使“2”朝上的可能性为3
1。
写出你的设计方案。
6、桌上有3张卡片,点数分别是1、2、3。
①先填写下表,然后想一想两张卡片上的点数之和有几种情况?
点数 1 2
3 1 / 3 2 / 5 3
5
/
②这个游戏规则公平吗?如果这样的规则不公平,你能设计一个公平的规则吗?
7、摸球游戏。
(盒子有10个红球、5个黄球) ①甲、乙两人分别摸球(各莫10次)。
②记录两人摸到黄球的次数。
次数 1 2 3 4 5 6 7 8 9 10 甲 乙
③统计表中数据,甲:( )次;乙:( )次;胜者:( )。
