习题课-拉氏变换31页PPT
合集下载
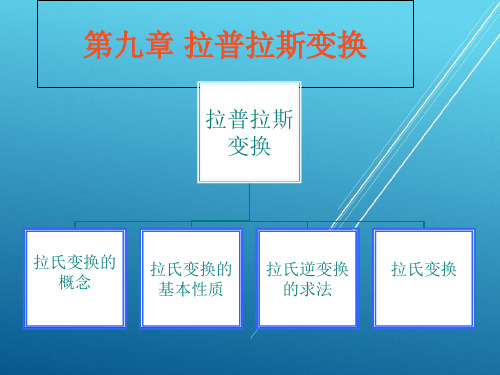
高数第10章 拉普拉斯变换PPT课件
L [sit]n dtarc t t an arc stan
t s t2 1
s2
或
L [stit]n s t2 d 1 令 tt u 11 s 0 1 d u 2u 0 1 s1 d u 2u aru c0 1 s ta arnc 1 st
第三节 拉氏逆变换的运算
❖ 重点:拉氏逆变换的求法 ❖难点:拉氏逆变换的求法
5. 积分性质: L[f(t)]F(s) ,( s 0 ) ,且 f ( t ) 连续,则
L[1f(x)dx]L[f(t)]F(s)
0
s
s
性质5表明,一个函数积分后取拉氏变换,等于这个函数
的拉氏变换除以参数 s .
性质5可以推广到有限次积分的情形:
n次
t t
L[ dt dt 00
t 0
f(t)dt]Fs(ns)
(s1)2 3
(s1)2 3
24
24
f(t)e2 t co3 st3e2 t sin 3t
2
2
例2
求
F(s)s2
s3 3ss
的拉氏逆变换。
解: 先将F (s) 分解为两个简单分式之和,
s 3 s 3 AB s2 3 ss (s 1 )s( 2 ) s 1s 2
其中AB为待定的常数,上式两边同乘以(s1)s(2),得
1 s
1 ss
e as
1 s
n!
(s ) n1
13
et sin t
14
et cost
15
tet sint
16
tet cost
17
sht
(s )2 2
s (s )2 2
2(s ) [(s )2 2 ]2
《拉氏变换详解》课件

积分性质
积分性质
若 $f(t)$ 的拉普拉斯变换为 $F(s)$, 则 $int_{0}^{infty} f(t) dt$ 的拉普拉 斯变换为 $- frac{1}{s} F(s)$。
应用
积分性质在求解初值问题和极值问题 时非常有用,可以方便地得到原函数 的表达式。
微分性质
微分性质
若 $f(t)$ 的拉普拉斯变换为 $F(s)$,则 $f^{(n)}(t)$ 的拉普拉斯变换为 $s^{n} F(s) - s^{n-1} f(0-) - s^{n-2} f'(0-) - ldots - f^{(n-1)}(0-)$。
卷积定理
总结词
卷积定理是拉普拉斯变换的一个重要特性, 它描述了函数与其导数之间的卷积关系。
详细描述
卷积定理表明,对于任意实数t,如果函数 f(t)与其导数f'(t)的拉普拉斯变换都存在,则 它们之间的卷积结果等于零。这个定理在信 号处理、控制系统等领域有着广泛的应用, 可以帮助我们更好地理解和分析函数的性质
,再通过反变换得到 (y(t))。
控制系统的稳定性分析
总结词
通过拉普拉斯变换,可以分析控制系统的稳定性,为系 统设计和优化提供依据。
详细描述
对于线性时不变控制系统,通过拉普拉斯变换,可以将 其转化为传递函数的形式。根据传递函数的极点和零点 分布,可以判断系统的稳定性。如果所有极点都在复平 面的左半部分,则系统是稳定的。如果极点在右半部分 或等于零,则系统是不稳定的。此外,系统的动态性能 也可以通过传递函数的极点和零点分布进行分析和优化 。
03
动态行为。
2023
PART 02
拉普拉斯变换的应用
REPORTING
在微分方程中的应用
拉氏变换课件

(指数式) A Ae A A cos j A sin (三角式)
j
机械工程控制基础
有复数
拉氏变换
3) 复变函数、极点与零点的概念
s j ,以s为自变量,按某一确定法则
构成的函数为复变函数,记作:
G( s) u jv
若
K ( s z1 )(s z2 ) ( s zm ) G( s) s( s p1 )(s p2 ) ( s pn )
称为复数A的虚部,表示为 =Im[A]
机械工程控制基础
2) 复数的表示方法
+j
b
0
拉氏变换 模
A
A
幅角
a
+1
a. 点表示法
( , ) b. 向量表示法(极径)
A cos A sin
A a b
2 2
b tan a
机械工程控制基础
拉氏变换
c.三角表示法和指数表示法
从数学的角度讲:拉普拉斯变换是求解微分方程的得 力工具
机械工程控制基础
2 拉氏变换的定义
设函数f(t)满足:
1f(t)实函数; 2当t<0时 , f(t)=0; 3当t0时,f(t)的积分 具有有限个第一类间断点
拉氏变换
0
st s的某一域内收敛, f (t )e在 dt
则函数f(t)的拉普拉氏变换存在,并定义为:
证明:
f (t )] F (s a)
L[e
at
f(t)] e
0 (s a)t
at
f(t)e dt
st
f(t)e
0
j
机械工程控制基础
有复数
拉氏变换
3) 复变函数、极点与零点的概念
s j ,以s为自变量,按某一确定法则
构成的函数为复变函数,记作:
G( s) u jv
若
K ( s z1 )(s z2 ) ( s zm ) G( s) s( s p1 )(s p2 ) ( s pn )
称为复数A的虚部,表示为 =Im[A]
机械工程控制基础
2) 复数的表示方法
+j
b
0
拉氏变换 模
A
A
幅角
a
+1
a. 点表示法
( , ) b. 向量表示法(极径)
A cos A sin
A a b
2 2
b tan a
机械工程控制基础
拉氏变换
c.三角表示法和指数表示法
从数学的角度讲:拉普拉斯变换是求解微分方程的得 力工具
机械工程控制基础
2 拉氏变换的定义
设函数f(t)满足:
1f(t)实函数; 2当t<0时 , f(t)=0; 3当t0时,f(t)的积分 具有有限个第一类间断点
拉氏变换
0
st s的某一域内收敛, f (t )e在 dt
则函数f(t)的拉普拉氏变换存在,并定义为:
证明:
f (t )] F (s a)
L[e
at
f(t)] e
0 (s a)t
at
f(t)e dt
st
f(t)e
0
拉氏变换详解ppt课件

a
0
a
令t / a , 则原式 f ( )e
0
sa
ad aF (as)
9
(8)卷积定理 两个原函数的卷积的拉氏变换等于两个象函 数的乘积。 t 即 L[ f (t ) f ( )d ] F ( s) Nhomakorabea ( s)
0 1 2 1 2
证明: L[ f1 (t ) f 2 ( )d ] [ f1 (t ) f 2 ( )d ]e dt
原函数之和的拉氏变换等于各原函数的拉 氏变换之和。 (2)微分性质 若 L[ f (t )] F ( s) ,则有 L[ f (t )] sF (s) f (0) f(0)为原函数f(t) 在t=0时的初始值。
3
证:根据拉氏变换的定义有
L[ f (t )] f (t )e dt s f (t )e dt f (t )e
st st 0 0
st 0
sF ( s) f (0)
原函数二阶导数的拉氏变换
L[ f (t )] sL[ f (t )] f (0) s[ sF ( s) f (0)] f (0) s 2 F ( s) sf (0) f (0)
14
2. 拉式反变换——部分分式展开式的求法
M (s) b0 s b1s bm1s bm F ( s) n (m n) n 1 D(s) s a1s an1s an
m
m1
(1)情况一:F(s) 有不同极点,这时,F(s) 总能展开成如下简单的部分分式之和
f (t ) L [ F ( s)] t 1 e
0
a
令t / a , 则原式 f ( )e
0
sa
ad aF (as)
9
(8)卷积定理 两个原函数的卷积的拉氏变换等于两个象函 数的乘积。 t 即 L[ f (t ) f ( )d ] F ( s) Nhomakorabea ( s)
0 1 2 1 2
证明: L[ f1 (t ) f 2 ( )d ] [ f1 (t ) f 2 ( )d ]e dt
原函数之和的拉氏变换等于各原函数的拉 氏变换之和。 (2)微分性质 若 L[ f (t )] F ( s) ,则有 L[ f (t )] sF (s) f (0) f(0)为原函数f(t) 在t=0时的初始值。
3
证:根据拉氏变换的定义有
L[ f (t )] f (t )e dt s f (t )e dt f (t )e
st st 0 0
st 0
sF ( s) f (0)
原函数二阶导数的拉氏变换
L[ f (t )] sL[ f (t )] f (0) s[ sF ( s) f (0)] f (0) s 2 F ( s) sf (0) f (0)
14
2. 拉式反变换——部分分式展开式的求法
M (s) b0 s b1s bm1s bm F ( s) n (m n) n 1 D(s) s a1s an1s an
m
m1
(1)情况一:F(s) 有不同极点,这时,F(s) 总能展开成如下简单的部分分式之和
f (t ) L [ F ( s)] t 1 e
优选补充资料拉氏变换ppt

ur
Ri
1 C
idt
uc
1 C
idt
(2 1)
式中: i为流经电阻R和电容C的电流,消去中间变
量i,可得:
RC
duc dt
uc
ur
(2 2)
令 RC T(时间常数),则微分方程为:
T
duc dt
uc
ur
(2 3)
北京航空航天大学
• 例2. 设有一弹簧•质 量• 阻尼动力系统如 图所示,当外力F(t)作 用于系统时,系统将
产生运动,试写出外 力F(t)与质量块的位移 y(t)之间的动态方程。 其中弹簧的弹性系数 为k,阻尼器的阻尼系 数为f,质量块的质量 为m。
F(t) f
k M y(t)
解:分析质量块m受力,有
外力F,
弹簧恢复力 Ky(t)
阻尼力 fdy(t) / dt
F(t)
惯性力 md 2 y / dt 2
由于m受力平衡,所以
1 lim
(m 1)! ss1
d m1 dsm1
[( s
si
)m
A(s) B(s)
eskt ],
t 0
f
(t)
n k m1
( ) A sk eskt B(sk )
1 lim
(m 1)! ss1
d m1 dsm1
[( s
si
)m
A(s) B(s)
eskt ],
t 0
例2
求
F
(s)
1
s (s 1)2
4)终值定理
lim x(t) lim sX (s)
t
s0
5)初值定理
x(0) lim x(t) lim sX (s)
拉式变换课件

F s L f t f t estdt
0
式中,s为复数变量;f t 为原函数;F s为象函数。
Page 4
拉氏变换的定义式:
记做
f (t) LT F (s) f (t)est dt 0
L [ f (t) ]= F (s) 或 f (t) LT F (s)
df (t) dt
est
f (t)
0
0
(s)e
st
f (t)dt
sF (s)
f (0 )
得证。
?
Page 23
uv'dx uv vu'dx
3.1.2 拉氏变换的性质
当 f(0)=f ’(0)=…f(n-1)(0)=0,则有:
L
2 s j0 s j0 s2 02
Page 20
பைடு நூலகம்
sin 0t
1 2j
(e j0t
e
) j0t
例:
L[sin 0t ]
1 2j
L[e
] j0t
1 2j
L[e
] j0t
1 2j
( s
1
j0
s
1
j0
)
0 s2 02
Page 21
3.1.2 拉氏变换的性质
(二)、 时域微分(differentiation)的拉氏变换
若L[ f (t)] F(s)
L
df (t dt
)
sF (s)
f
(0)
证明
0
式中,s为复数变量;f t 为原函数;F s为象函数。
Page 4
拉氏变换的定义式:
记做
f (t) LT F (s) f (t)est dt 0
L [ f (t) ]= F (s) 或 f (t) LT F (s)
df (t) dt
est
f (t)
0
0
(s)e
st
f (t)dt
sF (s)
f (0 )
得证。
?
Page 23
uv'dx uv vu'dx
3.1.2 拉氏变换的性质
当 f(0)=f ’(0)=…f(n-1)(0)=0,则有:
L
2 s j0 s j0 s2 02
Page 20
பைடு நூலகம்
sin 0t
1 2j
(e j0t
e
) j0t
例:
L[sin 0t ]
1 2j
L[e
] j0t
1 2j
L[e
] j0t
1 2j
( s
1
j0
s
1
j0
)
0 s2 02
Page 21
3.1.2 拉氏变换的性质
(二)、 时域微分(differentiation)的拉氏变换
若L[ f (t)] F(s)
L
df (t dt
)
sF (s)
f
(0)
证明
最新第5章 拉氏变换分析 习题课精品课件

d f t
dt
d2 dt 2
f
t
1
1
1
o
1
1
2t
o
1
2t
2
图4-2(b) 第七页,共25页。
显然(xiǎnrán)
L
d2 f dt
t
2
Lδ t 2δ t 1 δ t 2
1 es
2
根据(gēnjù)微分性质
L
d2 d
f t
t
2
s2F
s
f 0
sf
0
由图4-2(b)可以(kěyǐ)看出
1
F s F1sF1s
而
F1s
1 s
1
es
所以(suǒyǐ)
Fs
1 s2
1 es
2
o
1
t
图4-2(c)
第九页,共25页。
例4-3
应用微分(wēi fēn)性质求图4-3(a) f1t , f2(t), f3 t 象函数(há
下中面的说明应用微分性质应注意的问题,图4-3(b)是
f1t ,
2r1
(t)
r2
(t)
e(t)
r1 (t)
dr2 (t) dt
2r2
(t)
0
第二十二页,共25页。
解:对方程组求拉氏变换(biànhuàn),有: S R1(s) -r1(0) +2R1(s)- R2(s)=1/S (1) - R1(s)+S R2(s)- r2(0)+2 R2(s)=0 (2)
f 0 0, f 0 0
于是
s2F s 1 es 2
F s 1 1 es 2 s 2 第八页,共25页。
拉氏变换习题课PPT课件
=13F 12-1iω-2+1iω+1+1iω-1-1iω
F
1 1 β+ iω
=
ute-βt,
F
1 1 β- iω
=
u
teβt翻转性质
所以xt=
1 3
u-
te2 t
-
ute-2 t
+
ute-
t-
u-
tet
1
3
e2t -
et
t< 0
= 0
t= 0
1
3
e- t - e-2t
t> 0
.
32
0
1+ 1 - iω
1 1 + iω
=
2 1 + ω2
对原方程两边进行付氏变换得:
iω X
s
4
1 iω
X
s =
2 1 + ω2
所以
X
s =
- 2 iω 1 + ω2
4
1 + ω2
=
1 2 iω 3 4 + ω 2
-
2 iω 1 + ω2
.
31
xt=13F 142+iω ω2 -12+iω ω2
s
1 1
s
1 1
2 s
=
-
1 t
e-t
+
et
-
2
.
21
p1 0 0
3 . ( 8 )
计算 L
-1
1 s2 + 2s + 2
2
L
-1
1 s2 + 2s + 2
F
1 1 β+ iω
=
ute-βt,
F
1 1 β- iω
=
u
teβt翻转性质
所以xt=
1 3
u-
te2 t
-
ute-2 t
+
ute-
t-
u-
tet
1
3
e2t -
et
t< 0
= 0
t= 0
1
3
e- t - e-2t
t> 0
.
32
0
1+ 1 - iω
1 1 + iω
=
2 1 + ω2
对原方程两边进行付氏变换得:
iω X
s
4
1 iω
X
s =
2 1 + ω2
所以
X
s =
- 2 iω 1 + ω2
4
1 + ω2
=
1 2 iω 3 4 + ω 2
-
2 iω 1 + ω2
.
31
xt=13F 142+iω ω2 -12+iω ω2
s
1 1
s
1 1
2 s
=
-
1 t
e-t
+
et
-
2
.
21
p1 0 0
3 . ( 8 )
计算 L
-1
1 s2 + 2s + 2
2
L
-1
1 s2 + 2s + 2
