第1章矢量分析
第1章(矢量分析)

矢量分析与张量初步第一章矢量分析U STU STU ST标量(数量):有大小,没方向的物理量。
矢量:既具有大小又具有方向的物理量,矢量又称为向量。
矢量与标量的根本区别是:有没有方向性。
如:温度、质量、角度、长度等。
如:力、速度、电场强度、力矩等。
矢量的模:矢量的大小。
矢量的模记为:或。
A K A ||A KU STU STU ST自由矢量:矢量平移后,其作用效果不变。
即自由矢量就是具有平移不变性的矢量。
FK 只考虑刚体的质心运动,作用力可以平移。
能不能平移?下面只讨论自由矢量。
如果要考虑刚体的转动,则作用力不能平移。
U STU STU ST始端在坐标原点的矢量常称为矢径,显然矢径的末端与直角坐标系中的三个坐标分量之间具有一一对应的关系,则矢径可用其末端的空间坐标来表示:①在直角坐标中的表示对矢量,始端平移到坐标原点,表示为:A Kr xi yj zk=++KK K K、、:单位矢量,分别指向三个坐标轴的正向。
i K j K k K x y z A A i A j A k=++K K K KU STU STU ST其中:为矢量的模,为指向矢量方向上的单位矢量。
R A A e A 三个:、和。
R βαcos cos cos A e i j kαβγ=++K K K KAKRxy zO因为222cos cos cos 1αβγ++=的直角坐标表示为A e K有几个独立坐标量?A Kr e =KU STU STU STOxe ρρK zA kK A K cos sin e i j ρϕϕ=+K K K三个:、和。
ρϕz 的直角坐标表示为e ρK在矢量的球坐标及柱坐标表示中,只要分别把单位矢量和的直角坐标表示代入,即得到矢量的直角坐标表示。
e ρKr e K 有几个独立坐标量?A K第一章矢量分析U STU ST U ST U STU STcos xA Aα=cos yA Aβ=cos zA A γ=(cos cos cos )A A i j k αβγ=++K K K K④方向余弦表示:设矢量与直角坐标三个坐标轴正向的夹角分别为、和,则:αγβA K用方向余弦()表示矢量:A Kcos ,cos ,cos αβγcos x A A α=这实际上就是直角坐标表示,因为:cos y A A β=cos z A A γ=U STU STU ST不能按大小排列)。
第1章 矢量分析

第1章 矢量分析§1.1 标量场与矢量场一、场的概念如果某物理量在空间每一时刻和每一位置都有一个确定的值,则称在此空间中确定了该物理量的场。
二、标量场与矢量场标量场:若所研究的物理量是一个标量,则称该物理量的场为标量场,例如:温度场、密度场、电位场。
),(t r u u =矢量场:若所研究的物理量是一个矢量,则称该物理量的场为矢量场,例如:力场、速度场、电场。
),(t r A A =三、静态场和时变场静态场:若物理量不随时间变化,则称该物理量所确定的场为静态场。
)(r u u =)(r A A = 时变场:若物理量随时间变化,则称该物理量所确定的场称为动态场或时变场。
),(t r u u=),(t r A A =标量场在空间的变化规律由其梯度来描述,矢量场在空间的变化规律由矢量场的散度和旋度来描述。
§1.2 矢量场的通量 散度一、矢量线 矢量场的通量 1、矢量线(1)矢量场的表示在矢量场中,各点的场量是随空间位置变化的矢量。
矢量场可以用一个矢量函数)(r A来表示。
在直角坐标系中表示为:),,()(z y x A r A=(2)矢量线在矢量场中,为了形象直观地描述矢量在空间的分布状况,引入了矢量线的概念。
矢量线:是一条空间曲线,在它上面每一点的场矢量都与其相切,并且用箭头来表示矢量线的正方向。
例如,静电场中的电力线、磁场中的磁力线等。
(3)矢量线方程0)(=⨯r A r d在直角坐标系下为:)()()(r A dzr A dy r A dx z y x == 2、矢量场的通量 通过面积元的通量:S d r A d⋅=Φ)(通过有限面积的通量:⎰⋅=ΦSS d r A)(通过闭合曲面的通量:⎰⋅=ΦS S d r A)(二、矢量场的散度 1、散度的定义在矢量场)(r A中的任意一点M 处作一个包围该点的任意闭合曲面S ,所限定的体积为τ∆。
矢量场)(r A在点M 处的散度记作A div ,其定义为:ττ∆⋅=⎰→∆SS d r A A div)(lim 0 2、散度在坐标系下的表示A A div ⋅∇=定义哈密顿算符:ze y e x e z y x ∂∂+∂∂+∂∂=∇(1)在直角坐标系中的表示zuy u x u A ∂∂+∂∂+∂∂=⋅∇ (2)在圆柱坐标系中的表示()zA A A A z∂∂+∂∂+∂∂=⋅∇φρρρρφρ11 (3)在球坐标系中的表示()()φθθθθφθ∂∂+∂∂+∂∂=⋅∇A r A r A r r r A r sin 1sin sin 1122 3、散度的性质(1) 散度是通量源的密度;0>⋅∇A表示该点有发出通量线的正通量源;0<⋅∇A表示该点有接收通量线的负通量源;0=⋅∇A表示该点无通量源。
第1章 矢量分析与场论基础
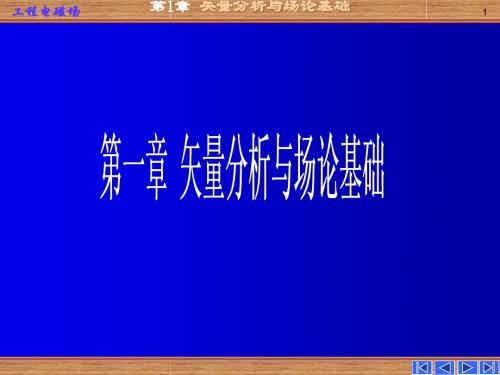
ex e y e y ez ez ex 0 ex ex e y e y ez ez 1
(4)矢量的矢积(叉积) 两矢量的叉积是一个矢量,其大小为两个矢量的大小与它们之
用单位矢量 en 表示。
间夹角 的正弦之积,它的方向垂直于包含两个矢量的平面,
工程电磁场
第1章 矢量分析与场论基础
10
1.2 三种常用的正交曲线坐标系
三维空间任意一点的位置可通过三条相互正交曲线的交点来 确定。 三条正交曲线组成的确定三维空间任意点位置的体系,称为
正交曲线坐标系;三条正交曲线称为坐标轴;描述坐标轴的量称
为坐标变量。 在电磁场与波理论中,三种常用的正交曲线坐标系为:直角 坐标系、圆柱坐标系和球坐标系。
矢量的加减符合交换律和结合律 交换律 A B B A 结合律 A ( B C ) ( A B) C
B B
A B
矢量的减法
A
工程电磁场
第1章 矢量分析与场论基础
6
(2)标量乘矢量
B sA ex sAx e y sAy ez sAz
第1章 矢量分析与场论基础
17
(3)圆柱坐标系与球坐标系的坐标变量之间的转换
r柱 r球 sin r球 r柱 z 2
2
z r cos r柱 z
arctg
工程电磁场
第1章 矢量分析与场论基础
18
1.3场的基本概念和可视化 1场的概念 “场”是指某种物理量在空间的分布。具有标量特征的物理量在空间 的分布是标量场,具有矢量特征的物理量在空间的分布是矢量场。 例如,温度场、能量场、电位场是标量场;电场、磁场、流速场与 重力场都是矢量场。 定义了场量的空间点称为场点。
01 第一章 矢量分析

⑴极限:设 F (t ) 在点 t 0 的某个邻域内有定义(但在 t 0 点
则称,当 t t0
⑵连续:若矢性函数 F (t )在点 t 0 的某个邻域内有定义,且 lim F t F t0 t t0 则称F (t ) 在 t t0 处连续。
(x)
ui
2
(
2 y 2 ) ( z ) ui ui
4、拉梅系数的几何意义
u i 线上的弧微分
x 2 y 2 z 2 dli ( ) ( ) ( ) dui hi dui ui ui ui
dli hi dui
表明:拉梅系数hi是M点处曲线坐标ui的微分dui与该坐标线ui 上弧微分的比例系数。
r(M )
hi
根据全微分运算法则
r r r dl d r du1 du 2 du3 u1 u2 u3
y 矢量线元
引入拉梅系数,矢量线元表示为
图1-7
dl h1du1e1 h2 du2 e2 h3 du3e3 dl1e1 dl2 e2 dl3 e3
2、拉梅系数
空间任意一点 M (u1 , u 2 , u 3 ) ,矢径
若M点在 u1 线上,则矢径 于是,单位矢量表示为
r e1 u1 r u1
r r (u1 , u 2 , u3 )
r (u1 , u 2 c2 , u3 c3 )
M
F (t )
说明:矢径函数对其矢端曲线弧长的导数为曲线上的单位矢量。
3、积分
⑴不定积分:若 A(t ) F (t ) ,则称 A(t )为 F (t )的一个原函数, F (t ) 的原函数的集合叫做的F (t ) 不定积分,记作 )d t A(t ) C F (t ⑵定积分:若矢性函数 F (t ) 在区间 [T1 , T2 ]上的极限
第一章 矢量分析
立了面积分和线积分的关系。从物理角度可以理解为斯托克 立了面积分和线积分的关系。从物理角度可以理解为斯托克 斯定理建立了区域 S 中的场和包围区域 S 的闭合曲线 l 上的 场之间的关系。因此, 中的场, 场之间的关系。因此,如果已知区域 S 中的场,根据斯托克 上的场,反之亦然。 斯定理即可求出边界 l 上的场,反之亦然。
Ψ = ∫ A ⋅ dS
S
通量可为正、或为负、或为零 当矢量穿出某个闭合面时, 通量可为正、或为负、或为零。当矢量穿出某个闭合面时, 认为该闭合面中存在产生该矢量场的源 认为该闭合面中存在产生该矢量场的源;当矢量进入这个闭合 面时,认为该闭合面中存在汇聚该矢量场的洞 )。闭合 面时,认为该闭合面中存在汇聚该矢量场的洞(或汇)。闭合
惟 一 性 定 理 亥姆霍兹定理 正交曲面 坐标系
10
第一章 矢量分析
标 积 与 矢 积 方向导数与梯度 通 量 与 散 度 环 量 与 旋 度 环 量 与 旋 度 无散场与无旋场 格 林 定 理
2. 旋度:旋度是一个矢量。若以符号 rot A 表示矢量 A 的旋 旋度:旋度是一个矢量。 具有最大环量强度的方向, 度, 则其方向是使矢量 A 具有最大环量强度的方向, 其大小等于对该矢量方向的最大环量强度, 其大小等于对该矢量方向的最大环量强度,即
惟 一 性 定 理 亥姆霍兹定理 正交曲面 坐标系
1
0 A⋅ B = A B
A⊥B
A // B
第一章 矢量分析
标 积 与 矢 积 方向导数与梯度
2.矢量的失积 2.矢量的失积
矢量的失积:代数定义: 矢量的失积:代数定义:
ex A × B = Ax Bx ey Ay By ez Az Bz
矢量分析

二、方向导数 在实际应用中,不仅需要宏观上了解场在空间的数值,还要知道在不同 方向上场变化的情况。方向导数表征标量场空间中,某点处场沿各个方向变 化的规律。
取等位面 u 1、定义:
x, y , z
增加的方向,相互垂直且满足右手螺旋法则
v ˆ ˆ ˆ 矢量表示: A = e x Ax + e y Ay + e z Az
v 位置矢量: r = e x x + e y y + e z z ˆ ˆ ˆ
v ˆ ˆ ˆ dr = e x dx + e y dy + e z dz 微分长度元:
(2)球面坐标系下矢量运算
v ˆ ˆ ˆ A = er Ar + eθ Aθ + eϕ Aϕ v ˆ ˆ ˆ B = er Br + eθ Bθ + eϕ Bϕ
v v ˆ ˆ ˆ A ± B = er ( Ar ± Br ) + eθ ( Aθ ± Bθ ) + eϕ ( Aϕ ± Bϕ )
v v A• B = Ar Br + Aθ Bθ + Aϕ Bϕ
e 单位矢量:ˆ ρ
ρ
,φ
ˆ , eφ
,z
ˆ , ez
0 ≤ ρ < ∞ , 0 ≤ φ ≤ 2π , − ∞ < z < ∞
ˆ ˆ ˆ e z = e ρ × eφ ˆ ˆ ˆ e ρ = eφ × e z ˆ ˆ ˆ eφ = e z × e ρ
ˆ ˆ ˆ ↑ e ρ 、eφ 、e z
分别代表ρ、φ、z 增加的方向,相互垂直且满足右手螺旋法则
ˆ 由于 θ、ϕ 不是常矢量,与 er
ˆ ∂er ˆ =eθ ∂θ ˆ ∂ eθ ˆ = −er ∂θ ˆ ∂ eϕ = 0 ∂θ
第1章-矢量分析

⎝
2⎠
⎝
2⎠
Ay
⎜⎛ x,y+Δy,z ⎟⎞ ⎝ 2⎠
=
Ay
(x,y,z)
+
∂Ay ∂y
(x,y,z)
Δy 2
+
1 2!
∂2 Ay ∂y2
( Δy )2 2
+ ...
得
ΔΨr
=
( Ay
+
∂Ay ∂y
Δy 2
+ .........) ΔxΔz
divA 直角坐标表示式的推导
11
§1.2通量、散度、散度定理
8
§1.2通量、散度、散度定理
作业:1.1-1,1.1-3,1.1-5
S为封闭面时: 若Ψ > 0, 有净通量流出,说明S内有源; 若Ψ < 0, 有净通量流入,说明S内有洞(负源); 若Ψ = 0, 则净通量为零,说明S内无源。
举例:
由《大学物理》知,电通量 Ψe = ∫sD ⋅ ds = Q(高斯定理) 水流的单位时间流量(米3/秒)= v ⋅ d s
A 矢量的模:
γ
β o
Ay
α Ax
y
A = A = Ax2 + Ay 2 + Az 2
x
A 的单位矢量:
Aˆ = A = xˆ Ax + yˆ A y + zˆ Az AA AA
= xˆ cosα + yˆ cos β + zˆ cosγ
2
§1.1矢量代数
二、标量积和矢量积
a) 标量积(点乘)
加减乘除
∂y 4π r 5
∂Dz = q r 2 − 3z 2
∂z 4π r 5
电磁场与电磁波—矢量分析

两个矢量的点积:写成
A B
其值为: A B AB cos
A
点积的性质:
θ
交换律 分配律 按乘数比例
A B C A B A C k A B kA B A kB
A B B A
若该物理量为矢量,则称矢量场, 可用矢性函数表示F(x,y,z); F(x,y,z,t) f(x,y,z,t)
若该物理量与时间无关,则该场称为静态场; 若该物理量与时间有关,则该场称为动态场或称为时变场。
第一章
矢量分析
笛卡尔坐标系
我们的标量函数(标量场)通常用笛卡 尔坐标系表示,我们的矢性函数也可以 用笛卡尔坐标系来表示 根据矢量的运算规则,多个矢量可以进 行矢量相加,反过来,一个矢量以可以 分解为多个矢量的和
B
第一章
矢量分析
两个矢量的叉积:写成 r F M 其值为: r F rF sin e n
M
r
F
第一章
矢量分析
叉积的性质:
不服从交换律 但服从分配 按乘数比例
A B C A B A C kA B k A B A kB
0
第一章
矢量分析
△z
z
若函数φ=φ(x, y, z)在点M0(x0, y0, z0)处可 微, cosα 、 cosβ 、 cosγ 为 l 方向的方向余弦, 则函数 φ在点M0处沿l方向的方向导数必定存 在,且为
γ M0 α
△x
ρ
β
M
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矢量场(vector field):如果空间中每一个点 所赋予的“量”为矢量,此空间就为矢量场。
1.1 标量场和矢量场 1.2 坐标系的转换 1.3 矢量运算 1.4 标量场的梯度 1.5 亥姆霍兹定理
d
a
a
y
1.2.3 球坐标系
P(r,, ) r球心到P距离
[0 r与+z轴的夹角 r在xoy面上的投 影()与+x轴的夹角
1)叉乘关系:(ar×)→(a ×)→(a ×)
1.2.3 球坐标系
2)点乘关系:ai•aj = 3)换算关系:
1 i=j 0 i≠j
x rsin cos cos y rsin sin sin z rcos
ax arsincosacoscosasin ay arsinsinacossinacos az arcosasin
1.2.3 球坐标系
4)位置矢量:r = ar r
5)线元矢量:
dlardrardars id n
z
ar
a
r•
O
y
a
x
1.2.3 球坐标系
6)矢量面元:
z
ar
dS = ardSr+adS+adS
A
B
矢量运算
矢量的加法 矢量的乘法 矢量的积分 矢量的散度 矢量的旋度
为了能对矢量进行运算,首先必须确定坐标系
z az
P •
r
O
a
a y
圆柱:r = a + azz
x
1.2.2 圆柱坐标系
5)线元矢量:(位移矢量)
直角坐标系中: dl = ax dx + aydy + azdz
圆柱坐标系中:
d l a d a d a zd z
z az
d
dz z • P
O
d
a
a
y
x
1.2.2 圆柱坐标系
6)面元矢量:
Oy
y
x
•
a
ay sin
a x ax cos
1.2.2 圆柱坐标系
注意:ax 、ay 、az是常矢量,模值为1,方向不变。而 a、a 模值为1,但方向随 变化,是 的函数,是变矢量。
a
ax sinay cos a
a
ax cosay sin a
4)位置矢量r :(从原点指
向某点)
直角:r = ax x + ay y + azz
z [
1.2.2 圆柱坐标系
1)坐标单位矢量叉乘关系: (a×)→( a ×)→(az×)
1 i=j
2)坐标单位矢量点乘关系: ai • aj = 0 i ≠ j
3)与直角坐标的换算关系:
x cos
y
sin
x2 y2
tan y x
a axcosaysin a axsinaycos
变量增加方向的三个单位矢量,用a1、a2、a3表示
• 坐标变量:三个独立的自由度,用e1、e2、e3表示
• 位矢:坐标原点到空间任一点的矢量。 e3
• e1、e2、e3呈右手螺旋关系——右手系
e2
e1
1.2.2 圆柱坐标系
P(,,z)
z az
•
P
O
a
a y
x
:P到z轴垂直距离 :在xoy面内的投影与+x轴的夹角
矢量(vector):指需要大小和方向才能完整表 示的物理量。如位移、速度、加速度、力、力 矩、动量等物理量。矢量也常称为向量。这些 量之间的运算并不遵循一般的代数法则,而遵 循特殊的运算法则。如矢量加法一般用平行四 边形法则。
1.1.1 相关定义
场(field):假设有一个n维空间,如果空间 的每一个点都具有某一特性的“量”,就可认 为这个空间包含有某种性质的“场”。 如温度 场、电场、磁场、电磁场。
dS 方向的定义:
•开表面:与面积外沿的绕向 呈右手螺旋关系
•闭合面:外法线方向
开表面面元方向
dS dS
闭合面面元方向
直角系中: dS = axdSx + aydSy + azdSz 其中 dSx =dydz,dSy =dxdz,dSz =dxdy 分别是dS在yoz面,xoz面和xoy面上的投影
1.2.2 圆柱坐标系
2R2(cos)
R
O
y
0
2R2(1cos)
x
1.1 标量场和矢量场 1.2 坐标系的转换 1.3 矢量运算 1.4 标量场的梯度 1.5 亥姆霍兹定理
矢量就是有方向的量,矢量包含了两种信息:幅 度和方向
矢量的表示:
用黑体符号来表示(如 A)或用上面带箭头的符号(如 )A
来表示
用有向线段(带箭头的线段)来表示:
1.2.1 正交曲线坐标系简介
常用的正交曲线坐标系有13种: 直角、圆柱、球、 椭圆柱、抛物柱、抛物面、旋转抛物面、 长旋转椭球、扁旋转椭球、椭球、双球、 圆锥、环
1.2.1 正交曲线坐标系简介
• 坐标线(轴):三张曲面两两正交相交而成的曲线 • 坐标原点(基准点):三条坐标线的交点
• 坐标单位矢量:空间任一点与坐标线相切且指向
a
dSr = r2sindd
r•
dS = rsinddr
O
y
dS = rddr
a
7)体积元:
x
d = dl1dl2dl3 = r2sindrdd
总结
1.2.3 球坐标系
例:计算面积分 S ar •dS ,其中S是半锥角为 的
圆锥面在半径为R的球面上割出的面积。
解: Sar•dSSdSr
z
2 R2sindd 00
圆柱系中: dS = a dS+ adS + azdSz
dS= d dz, dS =ddz,dSz=dd z
az
dS、dS 、dSz分别是dS 在圆柱侧面( 面)、过轴线
的半平面(面)和xOy面(z
d
dz z
面)上的投影。
7)体积元:
• P r
直角系中 dv = dx dy dz
O
圆柱系中dv = d d 2
tan
x2 y2
z
z
tan
y x
x
z
P•
r
O
ar a
y
a
1.2.3 球坐标系
ar a
axsincosaysinsinazcos axcoscosaycossinazsin
a axsinaycos
x
z
P•
r
O
ar a
y
a
注意:ar(,)、a(,)、a()均不是常矢量
第一部分 电磁场
第1章 矢量分析
1.1 标量场和矢量场 1.2 坐标系的转换 1.3 矢量运算 1.4 标量场的梯度 1.5 亥姆霍兹定理
1.1.1 相关定义
标量(scalar):只具有数值大小,而没有方向的 物理量。如质量、密度、温度、功、能量、速 率、时间、热量、电阻等物理量。这些量之间 的运算遵循一般的代数法则。
