矩阵论 第五章 Hermite矩阵和正定矩阵
矩阵理论-第七讲

由内积的
兰州大学信息科学与工程学院
矩阵理论第5讲-5
Hermite矩阵的正定性
– 推论
Hermite正定矩阵的行列式大于零
由 det A 12 L n 0 易知
矩阵理论-第七讲
兰州大学信息科学与工程学院 2004年
兰州大学信息科学与工程学院
矩阵理论第5讲-1
上节内容回顾
• 酉矩阵
– n个列向量是一个标准正交基 AH A I
• 酉相似下的标准形
AH A1
– Schur定理:任一复数方阵均可酉相似于上三角矩阵
U Cnn U 1 U H
U 1AU U H AU T
是Cn
上的向量范数。如果
ACnn x Cn
都有:
Ax A x
v
m
vБайду номын сангаас
则称矩阵范数 g m 与向量范数 gv 是相容的
矩阵范数中的第4条是矩阵范数与向量范数相容的必要条件:
ABx A(Bx) A Bx
v
v
m
v
因为 T sup{ Tx x : x 0}
T Tx x (x 0)
所以 AB sup{ ABx x : x 0} sup{( A Bx ) x : x 0}
兰州大学信息科学与工程学院
矩阵理论第5讲-3
Hermite矩阵的正定性
使得
U H AU diag(1, 2 , L n )
上式右边同乘以列向量:
1
y
2
M
n
左边同乘以行向量 yH,可得
2011年研究生《矩阵论》复习范围
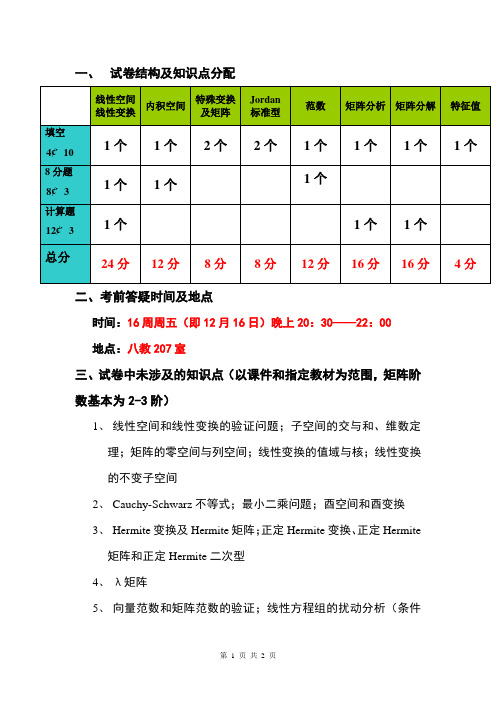
一、试卷结构及知识点分配
二、考前答疑时间及地点
时间:16周周五(即12月16日)晚上20:30——22:00
地点:八教207室
三、试卷中未涉及的知识点(以课件和指定教材为范围,矩阵阶数基本为2-3阶)
1、线性空间和线性变换的验证问题;子空间的交与和、维数定
理;矩阵的零空间与列空间;线性变换的值域与核;线性变换的不变子空间
2、Cauchy-Schwarz不等式;最小二乘问题;酉空间和酉变换
3、Hermite变换及Hermite矩阵;正定Hermite变换、正定Hermite
矩阵和正定Hermite二次型
4、λ矩阵
5、向量范数和矩阵范数的验证;线性方程组的扰动分析(条件
数除外)
6、矩阵级数;梯度矩阵及矩阵对矩阵的微分;能控性与能观测
性
7、矩阵的满秩分解
8、多项式特征值问题;Rayleigh商和广义Rayleigh商。
南京航空航天大学研究生课程《矩阵论》内容总结与习题选讲

《矩阵论》复习提纲与习题选讲Chapter1 线性空间和内积空间内容总结:z 线性空间的定义、基和维数;z 一个向量在一组基下的坐标;z 线性子空间的定义与判断;z 子空间的交z 内积的定义;z 内积空间的定义;z 向量的长度、距离和正交的概念;z Gram-Schmidt 标准正交化过程;z 标准正交基。
习题选讲:1、设表示实数域3]x [R R 上次数小于3的多项式再添上零多项式构成 的线性空间(按通常多项式的加法和数与多项式的乘法)。
(1) 求的维数;并写出的一组基;求在所取基下的坐标;3]x [R 3]x [R 221x x ++ (2) 在中定义3]x [R , ∫−=11)()(),(dx x g x f g f n x R x g x f ][)(),(∈ 证明:上述代数运算是内积;求出的一组标准正交基;3][x R (3)求与之间的距离;221x x ++2x 2x 1+−(4)证明:是的子空间;2][x R 3]x [R (5)写出2[][]3R x R x ∩的维数和一组基;二、 设22R ×是实数域R 上全体22×实矩阵构成的线性空间(按通常矩阵的加 法和数与矩阵的乘法)。
(1) 求22R ×的维数,并写出其一组基;(2) 在(1)所取基下的坐标; ⎥⎦⎤⎢⎣⎡−−3111(3) 设W 是实数域R 上全体22×实对称矩阵构成的线性空间(按通常矩阵的加法和数与矩阵的乘法)。
证明:W 是22R ×的子空间;并写出W 的维数和一组基;(4) 在W 中定义内积, )A B (tr )B ,A (T =W B ,A ∈求出W 的一组标准正交基;(5)求与之间的距离; ⎥⎦⎤⎢⎣⎡0331⎥⎦⎤⎢⎣⎡−1221 (6)设V 是实数域R 上全体22×实上三角矩阵构成的线性空间(按通常矩阵的加法和数与矩阵的乘法)。
证明:V 也是22R ×的子空间;并写出V 的维数和一组基;(7)写出子空间的一组基和维数。
智慧树答案矩阵论知到课后答案章节测试2022年

第一章1.方阵可逆是无0为其特征值的必要但不充分条件。
()答案:错2.相似矩阵有相同的()。
答案:特征值;行列式;迹3.矩阵的初等因子为()。
答案:4.方阵的每个特征值都是的最小多项式的根。
()答案:对5.酉矩阵的行列式为1。
( )答案:错第二章1.矩阵范数和谱半径之间有什么关系?( )答案:矩阵范数大于或者等于谱半径2.矩阵的1范数,2范数以及∞范数之间有何关系?( )答案:它们之间没有一定的关系3.如何计算矩阵的条件数?( )答案:矩阵的范数乘以其逆矩阵的范数4.矩阵范数与向量范数一定是相容的?( )答案:错5.矩阵范数所满足的性质比向量范数满足的性质多了哪一条?( )答案:相容性第三章1.对矩阵,若任意一种矩阵范数均满足,则.()答案:不一定成立;2.试分析:对矩阵,. ()答案:错3.对矩阵,. ()答案:对4.绝对收敛的矩阵级数一定收敛. ()答案:对5.对矩阵,若矩阵的某一种矩阵范数,则幂级数( ).答案:;第四章1.设矩阵是Hermite正定矩阵,则在保证分解矩阵主对角元素全为正的情况下,矩阵存在唯一的Cholesky分解。
()答案:对2.设矩阵,则矩阵,若矩阵为单位下三角矩阵,为上三角矩阵,则该分解称为Crout分解。
()答案:错3.设矩阵,则,其中为单位下三角矩阵,为上三角矩阵,为矩阵的Doolittle分解。
()答案:对4.Householder矩阵是酉矩阵。
()答案:对5.Givens矩阵是Hermite矩阵。
()答案:错第五章1. 1 设矩阵,且的个盖尔圆都是孤立的,则矩阵有个互不相同的是特征值.()答案:对2. 2 设矩阵,矩阵,矩阵,是矩阵的任意特征值,则下列说法正确的是().答案:;;3. 3 设矩阵是阶酉矩阵,,则的特征值满足().答案:对4.任何阶矩阵的盖尔圆都可以通过相似变换隔离成个孤立的盖尔圆。
()答案:错5.设矩阵有个孤立的盖尔圆,且原点不在这些盖尔圆中,则非奇异。
关于复正规矩阵的2个不等式

关于复正规矩阵的2个不等式沈浮;夏必腊;周堂春【摘要】给出了复正规矩阵的2个不等式,其中一个可看成是对文献[1]中定理3.9的推广,另一个是对文献[2]定理6.2.2的进一步研究,它们具有一定的理论价值和应用价值.【期刊名称】《江西科学》【年(卷),期】2014(032)001【总页数】3页(P5-7)【关键词】Hermite矩阵;正定矩阵;满秩矩阵;酉相似【作者】沈浮;夏必腊;周堂春【作者单位】解放军陆军军官学院数学教研室,安徽合肥230031;解放军陆军军官学院数学教研室,安徽合肥230031;解放军陆军军官学院数学教研室,安徽合肥230031【正文语种】中文【中图分类】O151.210 引言矩阵不等式是矩阵理论中的一个很重要内容。
随着矩阵理论的迅速发展及其在自然科学、工程技术和社会经济等领域的广泛运用,关于矩阵不等式的新结果层出不穷。
文献[1]中的定理3.9指出:当A是Hermite矩阵时,则有λmin(A)E≤A≤λmax(A)E。
文献[2]中定理6.2.2又指出:当A和B为2个非负定的Hermite矩阵时,则有0≤trAB≤λmax(A)trB≤rtA·trB。
这2个结果都是针对Hermite矩阵的,本文对复正规矩阵进行了研究,得出了更进一步的结论。
本文中,用Re(z)表示复数z的实部,用λmin (A)和λmax(A)分别表示Hermite矩阵A的最小特征值和最大特征值,用λRmin(A)和λRmax(A)分别表示复矩阵A 实部最小的特征值和实部最大的特征值,用tr(A)记矩阵A的迹,向量x的共轭转置用xH,E表示n阶单位矩阵。
1 基本概念及相关引理定义1:设A∈Cn×n,若对任意非零列向量x∈Cn×1,都有则称A为复正定矩阵(或复非负定矩阵),记作A>0(或A≥0)。
显然,当A为Hermite正定(非负定)矩阵时,它也是复正定(非负定)矩阵。
定义2:设A、B∈Cn×n,如果A-B是复正定矩阵(或复非负定矩阵),则称复矩阵A大于复矩阵B(或称复矩阵A大于或等于复矩阵B),记作A>B(或A≥B)。
Hermite二次型

如何建立判别方法
d1
1.设D
d2
,则D是正定的 di 0;
dn
2.若H阵A, B共轭合同,则 A正定 B正定;
d1
3.若H阵A与D
d2
共轭合同,则A正定 di 0。
dn
23
定理7
设 A是n nHermite阵,则下述条件等价: 1.A是正定的; 2.A的特征值均大于零; 3.A与I共轭合同; 4.存在可逆阵P使得A PH P; 5.A的各顺序主子式均大于零。
标准形中的正项个数称为其正惯性指数, 负项个数称为其负惯性指数。
18
惯性定理 矩阵形式:
若H阵A与
a1
b1
1
a2
,
2
b2
an
bn
共轭合同,则a1, a2 , , an与b1, b2, , bn中正、负项
个数相同。分别称为矩阵A的正、负惯性指数。
19
规范形
如果 n n Hermite 矩阵 A 的正、负惯性指数 分别是 p, q ,则 A 必定与矩阵
Ip O O
O
Iq
O
O O O
共轭合同。称此矩阵为 A 的规范形。
20
共轭合同的充分必要条件
定理6:n nHermite矩阵A, B共轭合同
A, B有相同的正、负惯性指 数。
21
正定性
定义:设A是H阵,f ( X ) X H AX ,
若对X 0 ,f ( X 0 ) 0,
则称f 是正定的,A是正定的H阵。
U ( y1, y2, , ys ), V (x1, y2 , , xn )H
则
A
U
D O
O O
V
浅谈Hermite矩阵的学习_任芳国
及任意 y∈Cn且 y≠0, 令 x= Py, 则 x∈ Cn 且 x ≠0, y3 (P3 A P ) y= x3 A x > 0. 故 P3 A P 是 H erm ite 矩阵. (2) ] (3) 对 H erm ite 矩阵 A. 由定理 2. 4 知存在酉矩阵 U , 使 U 3 AU = d iag (Κ1, Κ2, …, Κn) , 其中 Κi ( i= 1, 2, …, n) 为 A 的特征值, 由 (2) 知 d iag (Κ1, Κ2, …, Κn) 是正定矩阵, 则其中 Κi ( i= 1, 2, …, n ) 均为正数. ( 3) ] (4) 因为 A 特征值 Κ1, Κ2, …, Κn 均 为正数, 令 P 1 = d iag ( ( 1 Κ1 ) [12 ], ( 1 Κ2) [12 ], …, (1 Κ) [12 ]) P = U P1, 则 P 是可逆矩阵, 并且由 4. 3. 1 有, P 3 A P = (U P 1) 3 A (U P 1) = P 1U 3 AU P 1= I. (4) ] (5) 因为存在 n 阶可逆矩阵 P, 使得 P3 A P = I, 则令 Q = P- 1, 有 A = Q3Q; (5) ] (1) 因为存在 n 阶可逆矩阵 Q , 使得 Q = Q 3 Q , 则对任意 x∈Cn且 x≠0 都有 Q x≠0, 从而 x3 A x= (Q x) 3 (Q x) > 0; 故 A 是正定矩阵. 下面证明 (1) ] (6) 设 Κ为 A 的特征 值, x 为相应的特征值向量, 则A x= Κx, 因为 A 是正定矩阵, 所以 Κx3 x = x3 A x > 0 从而 Κ> 0, 因此 A 的特征值均为正 数, 又 A = U d iag (Κ1, Κ2, …, Κn)U 3 , 其中 Κi (i= 1, 2, …, n) 为 A 的特征值, 令 S= U d iag ( (1 Κ1) 1 2, (1 Κ2) 1 2, …, (1 Κ) 1 2) U 3 , 则 S 是 n 阶可逆 H erm ite 矩阵, 并
矩阵论复习
可求出 A(λ ) 的行列式因子 (3)将矩阵 A(λ )的不变因子 d 1 (λ ), d 2 (λ ),L , d r (λ ) 分解成 一次因式的幂: 一次因式的幂:
(λ − λ1 ) n1 , (λ − λ 2 ) n2 ,L , (λ − λ s ) ns
可求出 A(λ ) 的初等因子
4.Jordan标准形的求法 标准形的求法 4. (1)求矩阵 A 的初等因子
& & & C n = V λ1 + V λ 2 + L + V λ r
(3) A 的每一个特征值的几何重数等于代数重数. 的每一个特征值的几何重数等于代数重数. 的一维不变子空间的直和. (4) C n 可以分解成 A 的一维不变子空间的直和 的初等因子都是一次式. (5)A的初等因子都是一次式 的初等因子都是一次式 的最小多项式m(λ)没有重零点 没有重零点. (6)A的最小多项式 的最小多项式 没有重零点
即 A (ε 1 , ε 2 , L , ε n ) = (ε 1 , ε 2 , L , ε n ) A .
4.线性变换的值域与核 4.线性变换的值域与核 维线性空间V上的线性变换 ε 上的线性变换, 设A 是 n 维线性空间 上的线性变换,1 , ε 2 ,L , ε n 是 V 的一组基, 的一组基,A 在这组基下的矩阵是 A,则 , (1)A 的核为Ker ( A ) = {α ∈ V | A (α ) = 0}; (2)A 的值域为R( A ) = { A (α ) | α ∈ V };
α = x 1ε 1 + x 2 ε 2 + L + x n ε n .
2.线性子空间 2.线性子空间 是线性空间, 是 的非空子集, (1)设V是线性空间,W是V 的非空子集,则W是V 的 是线性空间 是 子空间的充分必要条件是
第五专题 矩阵的数值特征(行列式、范数、条件数、迹、秩、相对特征根)
第五专题矩阵的数值特征(行列式、迹、秩、相对特征根、范数、条件数)一、行列式已知A p×q, B q×p, 则|I p+AB|=|I q+BA|证明一:参照课本194页,例.证明二:利用AB和BA有相同的非零特征值的性质;从而I p+AB,I q+BA中不等于1的特征值的数目相同,大小相同;其余特征值都等于1。
行列式是特征值的乘积,因此|I p+AB|和|I q+BA|等于特征值(不等于1)的乘积,所以二者相等。
二、矩阵的迹矩阵的迹相对其它数值特征简单些,然而,它在许多领域,如数值计算,逼近论,以及统计估计等都有相当多的应用,许多量的计算都会归结为矩阵的迹的运算。
下面讨论有关迹的一些性质和不等式。
定义:n nii ii1i1tr(A)a====λ∑∑,etrA=exp(trA)性质:1. tr(A B)tr(A)tr(B)λ+μ=λ+μ,线性性质;2. Ttr(A )tr(A)=;3. tr(AB)tr(BA)=;4.1tr(P AP)tr(A)-=; 5. H Htr(x Ax)tr(Axx ),x =为向量;6. nnk ki i i 1i 1tr(A),tr(A )===λ=λ∑∑;从Schur 定理(或Jordan 标准形)和(4)证明; 7. A 0≥,则tr(A)0≥,且等号成立的充要条件是A=0;8. A B(A B 0)≥-≥即,则tr(A)tr(B)≥,且等号成立的充要条件是A=B (i i A B (A)(B)≥⇒λ≥λ);9. 对于n 阶方阵A ,若存在正整数k,使得A k =0,则tr(A)=0(从Schur 定理或Jordan 标准形证明)。
若干基本不等式对于两个m ×n 复矩阵A 和B ,tr(A H B)是m ×n 维酉空间上的内积,也就是将它们按列依次排成的两个mn 维列向量的内积,利用Cauchy-schwarz 不等式[x,y]2≤[x,x]﹒[y,y]得定理:对任意两个m ×n 复矩阵A 和B |tr(A H B)|2≤tr(A H A)﹒tr(B H B)这里等号成立的充要条件是A=cB,c为一常数。
北航博士入学考试矩阵大纲
北航线性代数和矩阵论考试大纲较全面、系统地考核考生掌握线性代数的基本理论、方法和某些应用的情况。
具体地,测试以下内容:一、矩阵和行列式:矩阵的概念和运算,矩阵行列式的定义、性质与计算,行列式的展开与Cramer 法则,矩阵逆的定义、性质与计算,初等变换与初等矩阵,矩阵在初等变换下的标准型,矩阵的分块及其运算,矩阵的广义逆。
二、线性方程组:初等变换与消元法,维向量空间的定义与性质,向量组的线性相关与线性无关,向量组的秩,齐次线性方程组的结构,非齐次线性方程组有解的判别准则及解的结构。
三、二次型与正定矩阵:对称矩阵的性质及其标准型,二次型的定义及其矩阵的表示,二次型的化简与分类,正定二次型,对称正定(半正定)矩阵的定义,性质和判定。
四、线性空间与欧几里得空间:线性空间的定义及其基本性质,线性空间的维数、基与坐标,线性子空间的定义、判定、性质及线性子空间的运算,特别是线性子空间的直和,线性空间的同构,欧几里得空间的定义、基本性质、标志正交基求法、正交变换与正交矩阵、子空间及其正交补、西空间的定义及其基本性质。
五、线性变换:线性变换的定义、性质、运算及其矩阵表示,线性变换的值域与核,线性变换的特征值与特征向量,矩阵的相似对角形,线性变换的不变子空间。
六、矩阵的行列式因子、不变因子和初等因子,矩阵相似的条件,矩阵的行列式因子、不变因子的初等因子,矩阵的Jordan标准型七、双线性函数:线性函数的定义与性质,对偶空间的定义及其性质,双线性函数的定义与性质,对称双线性函数与反对称函数的定义与性质。
矩阵论考试大纲:较全面、系统地考核考生掌握矩阵的基本理论、方法和某些应用的情况。
具体地,测试一下内容:一、线性空间与内积空间:线性空间的定义及其基本性质,线性空间的维数、基与坐标,线性子空间的定义、判定、性质及线性子空间的运算,特别是线性子空间的直和、线性空间的同构,内积的定义、基本性质、标准正交基及其求法、正交投影及其性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.1.3 •
Hermite n x 1 , · · · , xn ∈ C
n n
f (x1 , · · · , xn ) =
i=1 j =1
aij xi xj
aij = aji
Hermite a11 a12 · · · a1n a21 a22 · · · a2n A= . . . . . . . . . an1 an2 · · · ann
|yi |2
x H Ax =
i=1
|yi |2
s = 0, r = n
r
x H Ax = −
i=1
y = 0 x H Ax < 0 (4) (5) s=0 0<s<r 0 0 0 x Ax = −
H
|yi |2
s
x ∈ Cn
r i=s+1
i=1
x H Ax =
i=1
|yi |2 −
|yi |2
•
(1) (2) (3) (4) (5) •
A11 A12 AH 12 A22
, A11 ∈ Ck×k
A11 > 0
−1 A22 − AH 12 A11 A12 > 0
1 Ik −A− 11 A12 0 In−k
=
A11 0 −1 0 A22 − AH 12 A11 A12 A>0
A11 0 A11 A12 −1 AH 0 A22 − AH 12 A22 12 A11 A12 −1 A11 > 0 A22 − AH 12 A11 A12 > 0
1 D− 1 H 1 DD− 1 = D0 1 D− 1
)
λs ,
H
|λs+1 |, · · · ,
|λr |, 1, · · · , 1) A D0
−1 H PH 1 U AUP1 D1 = D0
•
•
(5.1.3)
D0
n
Hermite δ (A) )
A A
A ∈ Cn×n π (A), υ (A) (
5.1.1
f (x) = xH Ax Hermite x ∈ Cn x=0 x H Ax > 0 x ∈ Cn xH Ax ≥ 0 x H Ax x ∈ Cn x=0 x H Ax < 0 x ∈ Cn x H Ax ≤ 0 x H Ax x ∈ C n x H Ax Hermite f (x) = xH Ax s=r=n s=r s = 0, r = n s=0 0<s<r
•
5.3.1 A, A1 , B, B1 , C (1) A ≥ B(A > B) (2) A ≥ B(A > B)
n
Hermite −A ≤ −B(−A < −B); n P
PH AP ≥ PH BP(PH AP > PH BP) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) A ≥ B(A > B) k k A ≥ k B(k A > k B) ; A ≥ 0, −A ≥ 0 , A = 0 ; A≥0,B≥0, A+B≥0; A ≥ B, B ≥ C , A ≥ C ; A ≥ B, A1 ≥ B1 , A + A1 ≥ B + B1 ; A ≥ 0, B > 0 , A + B > 0 . A ≥ B, B > C A>C; A > B, P n×m , PH AP > PH BP ; A ≥ B, P n×m , PH AP ≥ PH BP ; A > 0(A ≥ 0), C > 0(C ≥ 0), AC = CA , AC > 0(AC ≥ 0) .
1 2 1 √ 8
z1 z2
• Hermite Hermite (1) (2) (3) s=r=n s=r
f (x) = xH Ax
n
s x Ax =
r i=1 H
r x=0 x ∈ Cn
n
0≤s≤r≤n y = 0 x H Ax > 0 x H Ax ≥ 0 |yi |2 x = 0 x H Ax ≤ 0 x x H Ax
Hermite
5.1
•
Hermite
Hermite
Hermite
2 3 − 2i 3 + 2i −5 −1 7 7 4 Hermite k A + pB S SH AS Hermite AB = BA Hermite
5.1.1
,
• Hermite (1) A (2) (3) (4) (5) A A A A B
x H Ax x H Ax x H Ax
5.1.9 (1) xH Ax (2) xH Ax (3) xH Ax (4) xH Ax (5) xH Ax
5.2
•
5.2.1 A
(
A n
)
Hermite A>0 A≥0 x ∈ Cn x ∈ Cn x=0 x H Ax > 0 xH Ax ≥ 0 A
• (1) (2) (3) (4) I>0 A>0 k>0 A>0 B>0 A≥0 B≥0 kA > 0 A+B>0 A+B≥0
•
(1) A (2) (3) A (4) (5) (6) •
5.2.2 n n n n
A
n
Hermite P P PH AP PH AP = A = QH Q A = S2 λ1 , λ2 , · · · , λn Q AQ ≥ 0
H
Ir 0 0 0
r = rank(A)
r Q Hermite S
•
λ
µ
A Ax = λx Ay = µy
x
y (1) (2)
(??) y H Ax = λy H x (??),µ = µH A = AH y H Ax = y H AH x = µy H x (λ − µ)y H x = 0 λ=µ x y
•
5.1.3
A ∈ Cn×n
A
Hermite
U
UH AU = Λ = diag(λ1 , λ2 , · · · , λn ) λ1 , λ2 , · · · , λn • 5.1.4 A ∈ Rn×n A QT AQ = diag(λ1 , λ2 , · · · , λn ) λ1 , λ2 , · · · , λn Q
Hermite Hermite B Hermite Hermite AB A−1
k k
Ak p
Hermite
Hermite
Hermite
•
5.1.1 A = (ajk ) ∈ Cn×n x ∈ C n x H Ax 5.1.2 (1) A (2) A (2) A n Hermite
A
Hermite
A
Hermite Hermite
A
Hermite f (x) = xH Ax
A
Hermite
x1 . x= . . xn
Hermite
Hermite
•
x = Py
P
n
y1 . y= . . yn
f (x) = xH Ax = y H By B = PH AP • Hermite λ1 y 1 y 1 + λ2 y 2 y 2 + · · · + λn y n y n Hermite •
LDU
L1 = UH 1 .
A = L1 DLH 1 dn )
L = L1 diag( d1 , · · · , L A = LLH .
•
5.2.2
A, B ∈ Cn×n ,
λ Ax = λ Bx
x ∈ Cn (3) x λ
λ . • B n
Ax = λ Bx
B−1 Ax = λx
(5.2.6)
•
A = S2 Hermite S
A = S2 = SH S
•
5.2.1
−1
A
n
λ1 , λ2 , · · · , λn QH AQ > 0
(1) A (2) Q n×m (3) |A| > 0 (4) tr(A) > λi (i = 1, 2, · · · , n) • 5.2.1 n Hermite A A= A>0 A11 Ik 0 H −1 −A12 A11 In−k A11 A12 AH 12 A22
•
5.2.6
Hermite
A A = LLH
L (5.2.3)
(??) . A n
A A
Cholesky .A A = L1 DU1 LDU
L1 , U1 di > 0(i = 1, 2, · · · , n).
D = diag(d1 , d2 , · · · , dn ) AH = A ,
H H H A = L1 DU1 = UH 1 D L1 = A
5.1.2 • 1.6.8 A,B ∈ Cn×n n B = PH AP A • B A n Hermite A P
5.1.5
Is 0 0 D0 = 0 −Ir−s 0 0 0 0n−r r =rank(A) s 5.1.3 A n ( U A = UΛUH Λ A A PH 1 ΛP1 = diag(λ1 , · · · , λs , λs+1 , · · · , λr , 0, · · · , 0) = D P1 λi > 0(i = 1, · · · , s), λj < 0(j = s + 1, · · · , r) D1 = diag( λ1 , · · · ,
