有理数乘除法、乘方复习
第3讲 有理数的乘除、乘方
第3讲有理数的乘除与乘方（教师讲义）一、教学目标1．理解有理数的乘法法则以及运算律，能运用乘法法则准确地进行有理数的乘法运算，会利用运算律简化乘法运算.2．掌握倒数的概念，会运用倒数的性质简化运算.3．了解有理数除法的意义，掌握有理数的除法法则，熟练进行有理数的除法运算.4．掌握有理数四则混合运算的步骤，熟练进行有理数的混合运算.5．理解有理数乘方的意义，掌握有理数乘方运算，进一步掌握有理数的混合运算.二、例子【知识点一：乘法运算】【例１】计算⑴11()24⨯-⑵1124⨯⑶11()()24-⨯-⑷25000⨯⑸3713 ()()(1)() 5697 -⨯-⨯⨯-【解法指导】掌握有理数乘法法则，正确运用法则，一是要体会并掌握乘法的符号规律，二是细心、稳妥、层次清楚，即先确定积的符号，后计算绝对值的积.解：⑴11111 ()() 24248⨯-=-⨯=-⑵11111() 24248⨯=⨯=⑶11111 ()()() 24248 -⨯-=+⨯=⑷250000⨯=⑸3713371031 ()()(1)()() 569756973 -⨯-⨯⨯-=-⨯⨯⨯=-【变式题组】01．⑴(5)(6)-⨯-⑵11()124-⨯⑶(8)(3.76)(0.125)-⨯⨯-⑷(3)(1)2(6)0(2)-⨯-⨯⨯-⨯⨯-⑸1111 12(2111)42612 -⨯-+-02．24(9)5025-⨯ 03．1111(2345)()2345⨯⨯⨯⨯---04．111(5)323(6)3333-⨯+⨯+-⨯【例２】已知两个有理数a 、b ，如果ab ＜0，且a ＋b ＜0，那么（ ）A ．a ＞0，b ＜0B ．a ＜0，b ＞0C ．a 、b 异号D ．a 、b 异号且负数的绝对值较大【解法指导】依有理数乘法法则，异号为负，故a 、b 异号，又依加法法则，异号相加取绝对值较大数的符号，可得出判断.解：由ab ＜0知a 、b 异号，又由a ＋b ＜0，可知异号两数之和为负，依加法法则得负数的绝对值较大，选D ．【变式题组】01．若a ＋b ＋c ＝0，且b ＜c ＜0，则下列各式中，错误的是（ ）A ．a ＋b ＞0B ．b ＋c ＜0C ．ab ＋ac ＞0D ．a ＋bc ＞002．已知a ＋b ＞0，a －b ＜0，ab ＜0，则a_____0，b______0，|a|_____|b|.03．(山东烟台)如果a ＋b ＜0，0b a>，则下列结论成立的是（ ） A ．a ＞0，b ＞0 B ．a ＜0，b ＜0 C ．a ＞0，b ＜0 D ．a ＜0，b ＞0【知识点二：除法运算】【例３】计算①(72)(18)-÷- ②11(2)3÷- ③13()()1025-÷ ④0(7)÷- 【解法指导】进行有理数除法运算时，若不能整除，应用法则1，先把除法转化成乘法，再确定符号，然后把绝对值相乘，要注意除法与乘法互为逆运算.若能整除，应用法则2，可直接确定符号，再把绝对值相除.解：①(72)(18)72184-÷-=÷= ②17331(2)1()1()3377÷-=÷-=⨯-=- ③131255()()()()10251036-÷=-⨯=- ④0(7)0÷-=【变式题组】 01．⑴(32)(8)-÷- ⑵112(1)36÷- ⑶10(2)3÷- ⑷13()(1)78÷-02．⑴12933÷⨯ ⑵311()(3)(1)3524-⨯-÷-÷ ⑶530()35÷-⨯【知识点三：乘方运算】【例4】计算（1）323-； （2）()524-- （3）()()2332---； （4） －34÷241×(－32)2． 【解法指导】n a 表示n 个a 相乘，根据乘方的符号法则，如果a 为正数，正数的任何次幂都是正数，如果a 是负数，负数的奇次幂是负数，负数的偶次幂是正数.解：（1）原式= （2）原式=（3）原式= （4）原式=【变式题组】（1）8十(－3)2×（-2）3 ⎥⎦⎤⎢⎣⎡-+-⨯-)95()32()3()2(22（3） 332)3()31()1(-⨯--- （4）已知223(2),1x y =-=- 求2008xy 的值；解：∵223(2),1x y =-=- x=2或x=-2 y=-1⑴当2,1x y ==-时，200820082(1)2xy =-=当2,1x y =-=-时，20082008(2)(1)2xy =-⨯-=-【知识点四：有理数的混合运算】【例５】计算[]24)3(23)5.01(1--⨯÷--- 【解法指导】先算乘方，再乘除，最后加减，有括号先算括号里的。
有理数的乘除乘方
有理数的乘、除及乘方运算一、知识要点：1． 有理数的乘法法则：（1） 两数相乘，同号 ，异号 ，并把 .任何数同0相乘，都得 .（2） 不等于0的数相乘，积的正负号由 的个数决定，当负因数有奇数个时，积为 ；当负因数有偶数个时，积为 .几个数相乘，有一个因数为0，积就为 .2． 乘积是 的两个数互为倒数3． 有理数的除法法则：除以一个数等于乘上 .两数相除，同号 ，异号 ，并把绝对值相除.0除以任何一个不等于0的数，都得0.4． 有理数的乘方法则：正数的任何次幂都是正数；负数的奇次幂是负数，负数的偶次幂是正数.二、典型例题：例1、计算：（1）⎪⎭⎫ ⎝⎛-⨯÷-43875.3 （2）532121⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-（3）⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛-⨯22176412（4）()[]2432611--⨯--例2、如果0,0><+ab b a ，则a 0，b 0. 如果()03<-ab ，则ab 0. 如果02>-b a ，则b .例3、已知a 、b 为有理数，下列说法中，正确的是（ ）A.若a ＞b,则a 2＞b 2B. 若︱a ︱＞b,则a 2＞b 2B. 若 a 3＞b 3,则a 2＞b 2 D. a ＞︱b ︱,则a 2＞b 2例4、已知：a 、b 互为倒数，c 、d 互为相反数，｜m ｜＝5，n 是绝对值最小的数，求5ab －(c+d)×2008 － n + m 的值。
例5、计算：(－2)100+(－2)101的是（ ）Ａ． 2100 Ｂ．－1 Ｃ．－2 Ｄ．－2100三、练习：1． 用四舍五入法把3.1415926精确到千分位是 .2． 用科学记数法表示302400，应记为 .3． 若m,n 互为相反数，xy 互为倒数，则（m ＋n ）＋5xy ＝ ；4． 若 3-x 与9+y 互为相反数，求y x -的值5． 一个数的相反数比它的本身大,则这个数是 （ ）A.正数B.负数C.0D.负数和06． 如果10<<a ，那么aa a 1,,2之间的大小关系是（ ） A ．a a a 12<< B ．a a a 12<< C ． 21a a a << D ． a a a<<21 7． 下列计算错误的个数是 （ ） ①221⎪⎭⎫ ⎝⎛=4 ②－52=25 ③2516542= ④811912=⎪⎭⎫ ⎝⎛-- ⑤－(－14 ) =1 ⑥()001.01.03=-- ⑦ 55=-=a ，a 则 ⑧ －a=－2则a = 2 8． A 、5个 B 、4个 C 、3个 D 、2个9． 平方等于4的数是 ，立方等于—8的数是 。
有理数乘除法知识点总结
七年级数学有理数乘除法知识点总结
有理数的乘法法则：
(1)两数相乘，同号得正，异号两数相乘得负。
(2)任何数与0相乘，积为0.
(3)若干个数相乘，有一个因数为0.积为0;各个因数不全为0.积的正负号由各个因数的符号决定。
(4)乘积是两数的倍数的关系，可以利用它比较大小。
有理数的除法法则：
(1)除以一个不等于0的数，等于乘这个数的倒数。
(2)两数相除，同号得正，异号两数相除得负。
(3)0除以任何一个不等于0的数，都得0.
重难点解析：
1、掌握有理数的乘除法法则，能够进行有理数的乘除法运算。
2、理解乘积是两数的倍数的关系，可以利用它比较大小。
3、掌握有理数的乘方运算，理解指数、底数、幂的概念，能够进行有理数的乘方运算。
4、难点在于理解有理数的乘除法法则，特别是对于一些特殊情况的处理，例如0作为除数的情况。
同时，有理数的乘方运算也是一个难点，需要理解其概念和运算方法。
总之，学生需要熟练掌握有理数的乘除法法则和乘方运算，理解其算理，能够在实际问题中灵活运用。
同时，还需要理解乘积是两数
的倍数的关系，能够利用它比较大小。
对于难点问题，需要通过多练习来加深理解。
有理数加减乘除乘方混合运算相关法则知识整理汇总
有理数加减乘除乘方混合运算相关法则知识整理一、知识整理填空答案符号计算绝对值加法同号取相同的符号绝对值相加异号取绝对值大的符号绝对值相减减法减去一个数等于加上这个数的相反数乘法同号取正绝对值相乘异号取负除法同号取正绝对值相除异号取负除以一个数等于乘以这个数的倒数二、一个运算中，含有有理数的加、减、乘、除、乘方等多种运算，称为有理数的混合运算.三、运算法则1、有理数的加法法则：1）同号两数的相加，取相同的符号，并把绝对值相加；2）异号两数相加，绝对值相等时和为0；绝对值不等时，取绝对值较大的数的符号，并用较大的绝对值减去较小的绝对值；3）一个数同0相加仍得这个数.2、有理数的减法法则: 减去一个数，等于加上这个数的相反数.3、有理数的乘法法则：1）两数相乘同号得正，异号得负，并把绝对值相乘；2）任何数与0相乘，积仍为0.4、有理数的除法法则: 1）除以一个数就是乘以这个数的倒数；2）两数相除同号得正，异号得负；并把绝对值相除；3）零除以任何非零的数得为零.注：0不能作除数5、有理数的乘方符号法则：1）正数的任何次幂都是正数；2）负数的奇次幂为负，偶次幂为正.四、有理数的运算律1、加法交换律：a+b=b+a2、加法结合律：(a+b)+c=a+(b+c)3、乘法交换律：ab=ba4、乘法结合律：(ab)c=a(bc)5、乘法分配律：a(b+c)=ab+ac五、有理数混合运算的法则：（1）先算乘方，再算乘除，最后算加减。
（2）如有括号，先进行括号里的运算。
1．先算乘方，再算乘除，最后算加减。
2．同级运算依照从左到右的顺序运算；3．若有括号，先小括号，再中括号，最后大括号，依次运算；。
有理数的乘除法、乘方运算
说一说我们学过的有理数的运算律：加法交换律：a +b=b+a ； 加法结合律：(a +b)+c=a +(b+c)；乘法交换律：a b=b a ； 乘法结合律：(a b)c=a (bc)；乘法分配律：a (b+c)=a b+a c这个算式里，含有有理数的加减乘除乘方多种运算，称为有理数的混合运算。
2．有理数混合运算的运算顺序规定如下：①先算乘方，再算乘除，最后算加减；②同级运算，按照从左至右的顺序进行；③如果有括号，就先算小括号里的，再算中括号里的，最后算大括号里的。
注意：①加法和减法叫做第一级运算；乘法和除法叫做第二级运算；乘方和开方(今后将会学到)叫做第三级运算。
②可以应用运算律，适当改变运算顺序，使运算简便。
②进行分数的乘除运算，一般要把带分数化为假分数，把除法转化为乘法；③同级运算，按从左往右的顺序进行，这一点十分重要。
三、课堂小结：理数混合运算的规律：1．先乘方，再乘除，最后加减；2．同级运算从左到右按顺序运算；3．若有括号，先小再中最后大，依次计算。
有理数的混合运算的关键是运算的顺序，运算法则和性质，为此，必须进一步对加，减，乘，除，乘方运算法则和性质的理解与强化，熟练掌握，在此基础上对其运算顺序也应熟知，只要这两个方面学的好，掌握牢在运算过程中，始终遵循四个方面：一是运算法则，二是运算律，三是运算顺序，四是近似计算，为了提高运算适度，要灵活运用运算律，还要能创造条件利用运算律，如拆数，移动小数点等，对于复杂的有理数运算，要善于观察，分析，类比与联想，从中找出规律，再运用运算律进行计算，至此，便可在有理数的混合运算中稳操胜卷。
1、有理数乘法法则：（1）两数相乘，同号得正，异号得负，并把绝对值相乘；（2）任何数同0相乘都得0；（3）多个有理数相乘：a ：只要有一个因数为0，则积为0。
b ：几个不为零的数相乘，积的符号由0的个数决定，当0的个数为奇数，则积为负， 当0的个数为偶数，则积为正。
有理数的加减乘除乘方混合运算专题训练(带答案)
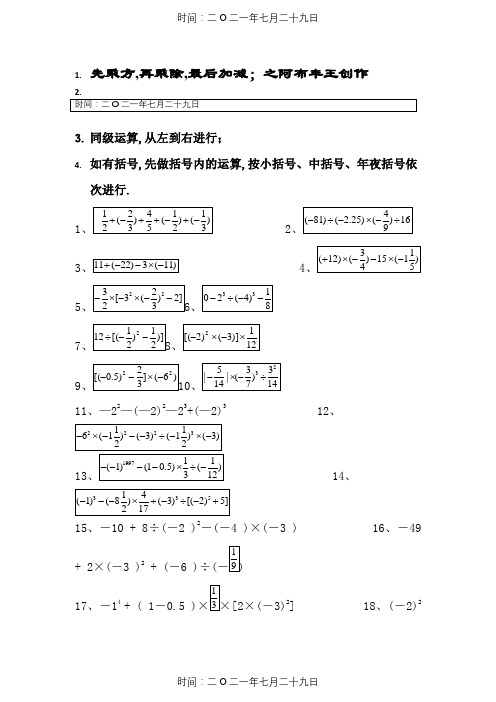
1.先乘方,再乘除,最后加减；之阿布丰王创作3.同级运算,从左到右进行；4.如有括号,先做括号内的运算,按小括号、中括号、年夜括号依次进行.1357911、—22—(—2)2—23+(—2)3 12、13、15、－10 + 8÷(－2 )2－(－4 )×(－3 ) 16、－49+ 2×(－3 )2 + (－6 )÷(17、－14 + ( 1－0.5 )[2×(－3)2] 18、(－2)2－2×[(2－3192123、 24、25、6－（－12、（-48）÷ 8 －（-5）27、420.25 2829、(－5)×6＋(－125) ÷(－5)3311、【基础题】计算：（1÷（2）（3（4（1（2（3（4（1（34（5（6（7（8；（9）10（1）11＋（－22）－3×（－11）；（2）（34；（5（6（7）（－6）（8）（1（2（34（5（6）－10＋84×3；（7（81－0.5）（1）（－8）×5－40；（2）（）÷（-（-2）；（3）-20÷5×（-3）÷15；（4）-3[-5+（÷-2）]；（5）－23÷2÷（2；（6×(－2.4)参考谜底1、-1/52、-13、224、95、96、 07、-48 8、-1 9、-15 10、-15/34311、-24 12、-89 13、3 14、215、-2016、23 17、2 18、24 19、-2820、9/1621、1 22、10 23、-1/12 24、104/325、926、1427、-3128、-81又1/81 29、-9 30、-2931、-1/5 32、91、【谜底】（1）17；（2（3）31；（4）－112、【谜底】（1）－10；（2）22；（3）－16；（4）3、【谜底】（1）1；（2）0；（3）42；（4（5）18；（6）0；（7）－4.64；（8（9）8；（104、【谜底】（1）22；（2）0；（3）－17；（4（5（6）－95；（7）－85；（8）6 .5、【谜底】（1）3；（2）1；（3）－54；（4）0；（5）（6）－20；（7）－2；（86、【谜底】（1）－80；（2）5.6；（3）－2；（4）16；（5）－复习有理数的乘除、乘方运算测试题一、填空题（每小题3分,共30分）1．3×（－2）=________,（－6=________．2．（－3）2的底数是________,；－32的底数是________,结果是________．3=________=________；（+8）÷（－=________．4．233=________2=________．5________=1________=－162．4=________．7．－32×（－5）23=________．83600平方公里,________．9．________；________10①23________222________3③32________22）3________）2二、判断题（每小题1分,共5分）11．零除以任何数都得零（）12．互为相反数的两个数的积为负数（）13．如果ab＞0,则a＞0且b＞0（）14．1除以一个非零数的商叫做这个数的倒数（）15．（－3）5暗示5个－3相乘（）三、选择题（每小题3分,共21分）16．下列说法,其中毛病的有①一个数与1相乘得原数；②一个数乘以－1得原数的相反数；③0乘以任何数得0；④同号两数相乘,符号不变．A．1个B．2个C．3个D．4个17．下列各对数：①1与1；②－1与1；③a－b与b－a；④－1与－1；⑤－5与|6|,其中互为倒数的是A．①②③B．①③⑤C．①③④D．①④18．下列各题中两个式子的值相等的是A．－23与（－2）3 B．32与23C．（－2）2与－22 D．|－2|与－|－2|19．下列结论中,其中正确的个数为①0的倒数是0；②一个不即是0的数的倒数的相反数与这个数的相反数的倒数相等；③其倒数即是自身的数是±1；④若a,b互为倒数,则－ab=－1．A．4 B．3C．2 D．120．下列各式中结果年夜于0的是A．1－910×3 B．（1－910）×3C．1－（9×3）10 D．（1－9）10×3 21．下列说法中正确的是A．一个数的平方必为正数B．一个数的平方必小于这个数的绝对值C．一个数的平方必年夜于这个数D．一个数的平方不成能为负数22．用科学记数法暗示的数2．89×104,原来是A．2890 B．2890000 C．28900 D．289000四、计算题（共35分）23．（3分）（－3）×（－5）×（+1224．（3分）－6÷（+3）÷（－4）×（+2）25．（3分）－5－626．（3分）（－81）÷16）27．（3分）－22×（－328．（3分）（－1）2000200120021）200329．（3分）（－2）×（－20011－200230．（331．（332．（3分）（－2.53）33．（5分）30五、解答题（934．已知A=a+a2+a3+……+a2000（1）若a=1,求A的值．（2）若a=－1,求A的值．一、1．－6 2 2．－3 9 3 －9 3－3245103平方公里9．＞＞＞＜13．×14．√15．√三、16．A 17．D 18．A 19．B 21．D 22．C四、23．－90 24．1 25．－3 2627．15 28．1 29．－200230．1 31．30 3233．－4五、34．（1）2000 （2）0。
1.3有理数的乘除及乘方
知识点 1：有理数乘法法则 法则：1、两数相乘，同号得正，异号 得负，并把绝对值相乘； 2、0 乘以任何数都得 0。
例：（1） 3 4
12
（2） 3 4
12
（3） 0 199
0
练习：仿上例，计算
3 5
8 5 6 3 3 4
6 3
0 125
9 6
2 6
读作：________________。
54 ，底数是___，指数是___，
读作：________________。 练习：2 仿写
练习：3
例： 3 2 2
32 22
9 4
仿上例，计算
1 3 2
例： 32 3 3 9 23 _________ _______. 34 _________ _______.
23 _________ _______.
读作：________________。
42 _________ _______.
32 ，底数是___，指数是___， 13 _________ _______.
读作：________________。
13 _________ _______.
43 ，底数是___，指数是___，
-5-
a 1、 底数
n指数
22 _________ _______. 33 _________ _______. 13 _________ ______22 3个 2 相乘
练习：1
72 _________ _______. 例： 72
2 2 3
43 _________ _______.
3 2 2
3 2 2
32
22
9 4
有理数的乘方_复习_ 3
有理数的乘方知识点一：有理数乘方的意义求几个 的积的运算叫做乘方．乘方的结果叫 ． 要点诠释：（1）一般地，n 个a 相乘，即：aaa aaa n....记作 ，其中a 叫 ，n 叫 ， 叫做a 的n 次幂或a 的n 次方，用图表示为：（2）乘方的运算：乘方是利用 来定义的． 是乘法的特 例，所以乘方的运算可以利用 的运算来进行．（3）乘方运算的符号法则：①正数的任何次幂都是 ；②负数的奇次幂是 ，负数的偶次幂是 ； ③任何一个数的偶次幂都是 ，如20a ≥．知识点二：有理数的混合运算有理数的混合运算是本章的重点之一，由于它的综合性强，所以又是难点，结合教材理解有理数的混合运算包含哪几种运算，掌握有理数的运算顺序和运算律．要点诠释：（1）有理数的混合运算中含有 、 、 、 、 等多种运算，称为有理数的混合运算．（2）有理数混合运算的顺序：①先乘方，再乘除，最后；②同级运算，从到进行；③如有括号，先做括号内的运算，一般按括号、括号、括号依次进行．（3）运算律的应用：①加法、乘法的所有运算律都能运用；②认真观察，选择恰当的运算律能简化运算，提高运算能力．知识点三：科学记数法把一个大于10的数表示成的形式（其中a是整数数位只有一位的数，≤| a |< ，n是正整数），这种记数法叫做科学记数法，如42 000 000＝．要点诠释：（1）1||10a≤<，a是整数数位只有一位的数，这一点要严格把握．（2）负数也可以用科学记数法表示，“-”照写，其他与正数一样，如-3000=．（3）一个小于10的数也可以用科学记数法表示，这些内容将在今后的内容中加以介绍．（4）在用科学记数法表示一个带有单位的数时，其表示结果也应带．（5）在用科学记数法表示一个数时，10的指数比原数的整数位少，反之一个以科学记数法形式表示的数，其整数数位比10的指数1．知识点四：近似数与准确数近似数：在实际问题中，由四舍五入得到的数或大约估计数，如π取3.14，体重约54 kg，这里3.14和54都是．准确数：与实际相符的数，如一年有12个月，12就是．要点诠释：（1）按要求取近似数时，采用的是，只要看要保留位数的下一位是舍还是入，与其它数位无关；对于比较大的数常用法表示．（2）近似数就是与实际接近的数，出现近似数的原因有两点：一是有时候不能得到完全准确的数，如太阳的半径大约是696 000千米；二是有时也没有必要弄得完全准确，如买10千克大米，有时可能多一点，有时也可能少一点．知识点五：精确度一个近似数四舍五入到哪一位，就称这个数精确到哪一位，精确度是指精确程度，如3.14精确到，那么就是精确度．精确度的表现形式有两种：①．②．注：近似数的精确度对结果影响很大，要根据实际需要决定近似数的精确度．知识点六：有效数字从一个数的左边第一个的数字起到止，所有的数字都是这个数的有效数字，如0.208的有效数字有个：_______________．类型一：有理数的乘方概念例1．（1）3的3次方，记作，其中底数是，指数是．（2）23的4次方，记作，其中底数是，指数是．（3）－2的5次方，记作，其中－2是，5是．举一反三：【变式1】24＝2×2×2×2＝；(－1)3＝＝；(－4)3＝＝；(－2)4＝＝．【变式2】计算：20072008 5665⎛⎫⎛⎫⋅⎪ ⎪⎝⎭⎝⎭类型二：有理数的乘方的符号法则例2．（1）正数的次幂都是正数，例如；负数的奇次幂是，例如；负数的偶次幂是，例如．（2）当n为正整数时(－1)4n+1＝，(－1)4n+2＝．思路点拨：（1）中所说的就是有理数乘方的符号法则，正数的任何次幂都是 ，负数的奇次幂是 ，负数的偶次幂是 ．（2）题中要注意的是4n+1是一个 ，而4n+2是一个 ． 举一反三：☆【变式1】3(2)-与32- （ ）A ．相等B ．互为相反数C ．互为倒数D ．可以是正数，也可以是负数类型三：有理数的混合运算例3．计算：52221(1)4(2)( 1.25)(0.4)339⎧⎫⎡⎤⎛⎫-⨯-÷-+-⨯-÷--⎨⎬ ⎪⎢⎥⎣⎦⎝⎭⎩⎭思路点拨：应按照 括号， 括号， 括号的先后顺序进行计算． 解：举一反三：【变式1】计算42813132(1)123242834⎛⎫⎛⎫-÷-⨯--+-⨯ ⎪ ⎪⎝⎭⎝⎭．分析：观察题目的特征，确定合理的运算顺序，能用简便方法的尽量用简便方法． 解：【变式2】如图所示，把一个面积为1的正方形等分成面积为12的矩形，接着把一个面积为12的矩形等分成面积为14的矩形，再把一个面积为14的矩形等分成两个面积为18的矩形，如此下去，试利用图形揭示的规律计算：11111111248163264128256+++++++= ．分析：直接计算比较烦琐，如果将数的计算问题转化 成 的计算，则很直观简单．类型四：科学记数法的应用例4．太阳是一个巨大的能源库，已知1 km2的土地上，一年内从太阳得到的能量相当于燃烧1.3×108kg煤所产生的能量，那么我国9.6×106km2的土地上，一年内从太阳得到的能量相当于燃烧a×10n kg煤．请利用所提供的材料，计算a，n的值分别是多少？思路点拨：实际上这仍然是一道常规题，先计算我国_________km2土地上一年吸收的能量相当于燃烧多少吨煤，然后用科学记数法表示，再求出对应的a，n的值．解：举一反三：【变式1】据推算，我国每天因土地沙漠化造成的经济损失为1.5亿元，若一年按365天计算，用科学记数法表示，我国一年因土地沙漠化造成的经济损失为亿元．解析例5．下列是由四舍五入得到的近似数，各精确到哪一位，各有几个有效数字？（1）15.28；（2）3.6万；（3）0.0403；（4）1.10×104．思路点拨：一个近似数精确到哪一位是指到哪一位，用科学记数法表示的近似数，如第（4）小题，可还原成，可知“1.10”中的在位．解：举一反三：【变式1】世界上最大的沙漠——非洲的撒哈拉沙漠可以粗略地看成是一个长方体，撒哈拉沙漠的长度大约是5149900米，砂层的深度大约是3.66米，已知撒哈拉沙漠中的沙的体积约为33345立方千米．（1）将沙漠的沙子的体积表示成立方米（保留2个有效数字）；（2）沙漠的宽度是多少？（3）如果一粒沙子的体积是0.0368立方毫米，那么撒哈拉沙漠中有多少粒沙子？（保留3个有效数字）解析：【变式2】用四舍五入法，按括号里的要求对下列各数取近似值．（1）3.708 49（精确到0.001）；（2）1.996（精确到百分位）；（3）0.0692（精确到千分位）；（4）30546（保留两个有效数字）；（5）5.04×104（精确到千位）．分析：运用四舍五入法，一定要先对精确位的进行四舍五入．较大数取近似a ”的形式，然后对进行取舍．值时，一般先用科学记数法写成“10n解：☆☆【变式3】一根竹竿长约1.56 m，那么它实际长度的范围是多少？解：练习题一、选择题1、118表示（ ）A 、11个8连乘 B 、11乘以8 C 、8个11连乘 D 、8个别1相加2、－32的值是（ ）A 、－9 B 、9 C 、－6 D 、63、下列各对数中，数值相等的是（ ）A 、 －32 与 －23B 、－23 与 (－2)3C 、－32 与 (－3)2D 、(－3×2)2与－3×224、下列说法中正确的是（ ）A 、23表示2×3的积B 、任何一个有理数的偶次幂是正数C 、－32 与 (－3)2互为相反数D 、一个数的平方是94，这个数一定是325、下列各式运算结果为正数的是（ ）A 、－24×5B 、(1－2)×5C 、(1－24)×5D 、1－(3×5)6 6、如果一个有理数的平方等于(－2)2，那么这个有理数等于（ ） A 、－2 B 、2 C 、4 D 、2或－2 7、一个数的立方是它本身,那么这个数是（ ）A 、 0B 、0或1C 、－1或1D 、0或1或－1 8、如果一个有理数的正偶次幂是非负数,那么这个数是（ ） A 、正数 B 、负数 C 、 非负数 D 、任何有理数 9、－24×(－22)×(－2) 3=（ ）A 、 29 B 、－29 C 、－224 D 、22410、两个有理数互为相反数，那么它们的n 次幂的值（ ）A 、相等B 、不相等C 、绝对值相等D 、没有任何关系 11、一个有理数的平方是正数,则这个数的立方是（ ） A 、正数 B 、负数 C 、正数或负数 D 、奇数12、(－1)2001＋(－1)2002÷1-＋(－1)2003的值等于（ ）A 、0 B 、 1 C 、－1 D 、2 二、填空题 1、(－2)6中指数为 ，底数为 ；－26中指数为 ，底数为 ；4的底数是 ，指数是 ；523⎪⎭⎫ ⎝⎛-的底数是 ，指数是 ，结果是 ；2、根据幂的意义，(－3)4表示 ，－43表示 ；3、平方等于641的数是 ，立方等于641的数是 ；4、一个数的15次幂是负数，那么这个数的2003次幂是 ；5、平方等于它本身的数是 ，立方等于它本身的数是 ；6、=⎪⎭⎫ ⎝⎛-343 ，=⎪⎭⎫⎝⎛-343 ，=-433 ，()()10110022-+-= ；7、()372⋅-，()472⋅-，()572⋅-的大小关系用“＜”号连接可表示为 ；8、如果44a a -=，那么a 是 ；9、()()()()=----20022001433221 ；10、如果一个数的平方是它的相反数，那么这个数是 ；如果一个数的平方是它的倒数，那么这个数是 ； 11、若032＞b a -，则b 0 三、计算题1、()42-- 2、3211⎪⎭⎫ ⎝⎛ 3、()20031- 4、()33131-⨯-- 5、()2332-+-6、()2233-÷-7、()()3322222+-+--8、()34255414-÷-⎪⎭⎫ ⎝⎛-÷9、()⎪⎭⎫ ⎝⎛-÷----721322246 10、()()()33220132-⨯+-÷---四、解答题 1、按提示填写：2、有一张厚度是0.2毫米的纸，如果将它连续对折10次，那么它会有多厚？3、某种细菌在培养过程中，每半小时分裂一次（由一个分裂成两个），若这种细菌由1个分裂为16个，则这个过程要经过多长时间？运算 加法 减法 乘法 除法 乘方结果称为 和4、你吃过“手拉面”吗？如果把一个面团拉开，然后对折，再拉开，再对折，……如此往复下去，对折10次，会拉出多少根面条？五、探究创新乐园1、你能求出1021018125.0⨯的结果吗?2、若a 是最大的负整数，求2003200220012000a a a a +++的值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
8
4
(2). 8 [ 1 ( 1 0.25 2) 2 1] (8 9)
76
33
（2）已知a,b互为相反数,c,d互 为倒数,m的绝对值是2,求
a b mcd 2004 的值.
m
幂的性质：
1、当指数是奇数时,负数的幂是____数. 2、当指数是____数时,负数的幂是正数. 3、正数的任何次幂都是____数. 4、0的任何正整数次幂是——。
1+3+5+7=42 1+3+5+7+9=25=52
……
根据各式前面的规律，猜测：
1+3+5+7+9+11 =
.
1+3+5+7…+(2n+1)= 自然数）
.（其中n是
(1).(48)
(8);(2).(
12)
(
3
).
25 5
解 : (1).( 48) (8) (2).( 12) ( 3)
(488) 6
25 5 ( 12)( 5)
25 3
4
5
例2：化简下列各式：
(1).12;(2). 45
3
12
解 : (1).12 12 3 4 3
(2). 45 45 (12) 15
A.a2=(-a)2
B. a2=|a2|
C. a3=(-a)3
D.-a3=(-a)3
5、平方等于它本身的数是——， 立方等于它本身的数是——，一个 数的平方等于它的立方的数是——。
6、判断下列各题是否正确
Байду номын сангаас
① 23=2 ×3
（
）
② 2+2+2=23
（
）
③ 23=2×2 ×2 （
）
7、计算：
3
2
4
a2
若a为有理数，则 是什么数？
针对性训练： 1、（-9）3 的底数是——，指数是——， 可读作____或——。
2、-93 的底数是——，指数是——，
可读作____或——。
3、在（-1）2005，（-1）2006，-22，
（-3）2这四个数中，最大的数和最小的 数的和是————。
4、若a是负数，则下列各式不正确 的是
(28 49 63)7
287 497 637
（2）
28 1 49 1 63 1
7
7
7
4 7 9 12
( 1 1 1) ( 1 ) 12 9 3 36
（3） 12 ( 1 1 1) 623
计算：
(1). 3.5 1 ( 3 );(2).56 (13) ( 1) (0.75)
_
33
4
_
3
3
4
_
1
3
2
4
8、1米长的小棒，第一次截去 一半，第2次截去剩下的一半， 如此下去，第5次后剩下的小 棒有多长？
1、若 a2 16，则a=_________；
2、若 (a 1)2 b 2 0 ，求 ab 的值
探索与研究
已知：
1+3=4=22 ， 1+3+5=9=32
12
4
例3：计算：
1.(125 5) (5);2. 2.5 5 ( 1)
7
84
解 : (125 5 ) (5) 2. 2.5 5 ( 1)
7
84
(125 5) 1 75
125 1 5 1 5 75
25 1 25 1
7
7
58 1 254
1
（1）下面的计算正确吗？你发现了什么？
有理数的乘除法、乘方 （复习）
• 计算：
• ①（-5）×（-6）；
解： （-5）×（-6）
= +（ 5×6）
= 30
② ( 1) 1 24
解： ( 1) 1 24
( 1 1) 24
1 8
1）如果a×b=0，则这两个数 （ C ）
A 都等于0， B 有一个等于0，另一个不等于0；
C 至少有一个等于0，
24
74
(3).(15)[1.75 (3 1 1) 5] 4
计算：
(1).18 6 (2) ( 1); 3
(2).11 (22) 3 (11)
(3).(0.1) 1 (100); 2
(4).2 1 ( 1 1) 3 (1 1)
5 3 2 11
4
计算：
(1).328 (0.25) 147 (0.125) 253 1 72 ( 1);
D 互为相反数
2）已知-3a是一个负数，则 （ A ）
A a>0 B a<0 C a≥0 D a≤0
3）两个有理数和为0，积为负，则这两
个数的关系是
（ D）
A 两个数均为0，
B 两个数中一个为0
C 两数互为相反数，
D 两数互为相反数，但不为0。
除以一个不等于0的数,等于乘这个
数的倒数. a b a 1 (b 0)
练习:
b
(1).(36) 9 =-4
(2).(12) ( 1) =+72 6
(3).(15) (3)=-5
(4).(8) ( 1) =+32 4
(5).0 (68) =0
两数相除,同号得_正__,异号得_负__,并把绝对值相 __除__.0除以任何一个不等于0的数,都得_0__.
例1:计算