第四章-特殊函数(上)-勒让德多项式和球谐函数
第四章-特殊函数(上)-勒让德多项式和球谐函数

2ll!dxl
k0
2lk!(lk)!
[2 l]
(1)k
k0
(2l2k)! xl2k 2lk!(lk)!(l2k)!
Pl(x).
3.勒让德多项式的积分表示
根据柯西积分公式的高阶导数,并取正方向积分有
i f(l)(z) l!
f() d
2πi C(z)l1
容易证明微分表示(4.1.10)也可表示为环路积分形式
4.2.1 勒让德多项式的性质 1. 勒让德多项式的零点 对于勒让德多项式的零点,有如下结论:
(i) P n ( x ) 的 n个零点都是实的,且在 (1,1) 内;
(ii) Pn 1 ( x ) 的零点与 P n ( x ) 的零点互相分离.
2. 奇偶性 根据勒让德多项式的定义式,作代换 x (x), 容易得到
P2n(0)(1)n2(22 nn n!)n !!(1)n(2 (n 2n )1 !)!!! (4.1.9)
式中记号 ( 2 n ) ! ! ( 2 n ) ( 2 n 2 ) ( 2 n 4 ) L 6 4 2
而 ( 2 n 1 ) ! ! ( 2 n 1 ) ( 2 n 3 ) ( 2 n 5 ) L 5 3 1
的项,即 k l
2
的项,应取 k m ax
[l] 2
,并且注意到
d l x 2 l 2 k ( 2 l 2 k ) ( 2 l 2 k 1 )[ 2 l 2 k ( l 1 ) ] x l 2 k d x l
因此有
1
dl
(x21)l
[2 l]
(1)k
(2l2k)(2l2k1)L(l2k1)xl2k
本章主要内容:勒让德多项式的来源、定 义、性质、生成与递推公式,球谐函数。
勒让德多项式

k 2 3P3 ( x) 5xP2 ( x) 2P ( x) 15 x3 9 x 1 2 2
勒让德多项式的性质
奇偶性
Pl(-x) = (-1)l Pl(x) 零点定理 L阶勒让德多项式为L次多项式,有L个零点。 正交性
– 正交性公式 – 模 – 正交性应用例题
完备性
(35cos 4 20cos 2 9)
勒让德多项式的图象
勒 让 德 多 项 式 的 图 象
母函数和递推公式
母函数 – 定义:u(x, r) =∑ Pl (x) r l – 形式:u(x, r) = ( 1-2rx + r2 )-1/2 – 推导 – 应用 递推公式 – 基本递推公式 – 证明 – 应用
球内解要求u (0, )有界,半通解化为 u
l 0
Al r l Pl (cos )
2
由边界条件得: Ax
l 0
Al a l Pl ( x )
Ax2 P ( x)dx k
2k 1 根据完备性:Ak 2a k
1
1
勒让德多项式的应用
例题 2
半径为a的球面上电势分布为 f = Acos2θ,确定球外空 间的电势 u 。
2
由边界条件得: Ax
l 0
Bl a l 1Pl ( x )
2k 1 k 1 根据完备性: k B a 2
1
1
Ax2 P ( x)dx k
勒让德多项式的应用
例题 3
一空心圆球区域,内半径为a,外半径为b,内球面上电势为 f = cosθ,外球面上电势为零,确定区域内电势u 。
解:定解问题为:u 0, a r b u |r a cos , u |r b 0
SphericalHarmonics球谐函数的理解与使用

SphericalHarmonics球谐函数的理解与使用球谐函数(Spherical Harmonics)是用于描述球对称性的函数。
它在数学、物理、计算机图形学等领域中具有广泛的应用。
本文将对球谐函数的理解与使用进行详细介绍。
首先,我们来了解球谐函数的定义。
给定单位球面上的点(x,y,z),球谐函数Yₗⁿ(x,y,z)定义如下:Yₗⁿ(x, y, z) = (-1)^m * sqrt((2ℓ+1)/(4π)*(ℓ-,m,)!/(ℓ+,m,)!)*Pₗ,m,(cosθ)*e^(imφ)其中,Yₗⁿ表示度为ℓ,阶为,m,的球谐函数;ℓ是非负整数,表示球谐函数的度;,m,<=ℓ,m是整数,表示球谐函数的阶;Pₗ,m,(cosθ)是勒让德多项式;θ是点(x, y, z)相对于x轴的极角;φ是点(x, y, z)相对于x轴的方位角;e是自然对数的底。
球谐函数具有下述性质:1.球谐函数是单位球面上的正交基,即不同的球谐函数之间在单位球面上的内积等于0。
2.Yₗⁿ(x,y,z)关于极角θ是奇函数,关于方位角φ是偶函数。
3.在单位球面上,球谐函数Yₗⁿ(x,y,z)的绝对值平方是一个常数,即,Yₗⁿ(x,y,z),²在球面上处处相等。
在物理学中,球谐函数被广泛应用于描述球对称的物理场。
例如,在量子力学中,球谐函数用于描述原子中的电子波函数;在电动力学中,球谐函数用于展开电磁场的球谐分量;在量子力学中,球谐函数用于描述自旋等。
在计算机图形学中,球谐函数也被广泛应用于实时渲染、全局光照以及球形图像处理等领域。
通过将光照场或图像投影到球谐函数系数上,可以实现基于球面光照的实时渲染。
球谐函数还可以用于创建全局光照环境贴图,用于增强场景的真实感。
此外,球谐函数还可以用于球形图像处理,例如球形全景图像的压缩和展开。
值得注意的是,球谐函数展开的精度和复杂度有一定的关系。
一般来说,较高阶的球谐函数能够更准确地近似光照场或图像,但计算复杂度也会增加。
球谐函数ylm

球谐函数ylm1. 什么是球谐函数球谐函数(Spherical Harmonics)是描述在球面上的物理和数学问题的一组函数。
球谐函数可以用于描述轴对称的空间分布,例如电荷分布、电磁场等。
球谐函数是平面波的三维推广,它描述了球对称下的波函数形式。
它在物理学、数学和计算机图形学等领域有广泛的应用。
球谐函数通常用Ylm(θ, φ)表示,其中θ是极角,φ是方位角。
2. 球谐函数的性质球谐函数具有以下一些重要的性质:2.1 正交性球谐函数在单位球面上是正交的,即不同的球谐函数之间的内积为零。
这个性质在解决物理和数学问题的时候是非常有用的,可以用来展开复杂的函数。
2.2 归一性球谐函数在单位球面上是归一的,即其平方的积分等于1。
这个性质保证了球谐函数在描述物理问题时的准确性,可以确保物理量的总能量是保持不变的。
2.3 奇偶性球谐函数具有奇偶性。
对于函数Ylm(θ, φ),当l为偶数时,其函数值是关于θ对称的;当l为奇数时,其函数值是关于θ反对称的。
2.4 旋转对称性球谐函数具有旋转对称性,即在球面上进行旋转变换后,球谐函数的形式不变。
这个性质保证了球谐函数在描述旋转对称系统时的准确性,如原子轨道和电磁场分布。
3. 球谐函数的计算球谐函数的计算可以通过递推关系或者数值方法来进行。
3.1 递推关系球谐函数Ylm(θ, φ)可以通过递推关系来计算,公式为:Ylm(θ, φ) = (-1)^m sqrt((2l+1) / (4π) (l-m) / (l+m)) Pnm(cosθ) e^(imφ)其中,Pnm(x)是勒让德多项式,可以通过递推关系Pnm(x) = (2n-1) * x * Pn-1m(x) - (n+m-1) * Pn-2m(x)来计算。
3.2 数值方法除了递推关系,还可以使用数值方法来计算球谐函数。
常用的数值方法包括插值法和数值积分法,可以根据具体问题的要求来选择合适的方法进行计算。
4. 球谐函数的应用球谐函数广泛应用于物理学、数学和计算机图形学等领域。
球谐函数 偏导

球谐函数偏导
球谐函数是一类特殊的函数,它们是由勒让德多项式和三角函数的乘
积组合而成的。
球谐函数在物理学的各个领域都有广泛的应用,如热
力学、电动力学、量子力学等。
此外,球谐函数也在图像与信号处理、计算机图形学中得到了应用。
首先,球谐函数的导数也十分重要。
球谐函数的定义域是单位球面上
的点,因此球谐函数的导数会在单位球面上产生向内或向外的法向量。
球谐函数和它们的导数在物理学中被广泛应用于描述旋转对称性、自
旋角动量和磁场等领域。
在这些应用中,球谐函数的导数被用于计算
旋转矩阵的元素、各向异性之间的耦合等问题。
其次,由于球谐函数具有特殊的正交性质,因此它们可以用来展开各
种函数。
这种展开叫做球谐函数展开。
球谐函数展开在图像与信号处理、计算机图形学中被广泛应用。
例如在计算机图形学中,球谐函数
展开被用来照亮、渲染物体,同时也被用来压缩和储存高动态范围图像。
此外,球谐函数展开也被用来进行信号分析和处理,如声音、图
像和视频信号的分析和压缩等。
最后,球谐函数还具有一系列的性质。
例如在三维空间中,球谐函数
可以用来描述电磁波、声波等的空间分布。
此外,在量子力学中,球
谐函数被用来描述粒子的自旋、角动量等,是量子力学中具有重要意义的函数。
总之,球谐函数作为一类特殊的函数,在物理学与计算机科学等领域都有广泛的应用。
球谐函数的偏导数、展开和性质等方面也具有重要意义。
因此,深入理解和应用球谐函数对于相关领域的研究和实践都具有十分重要的作用。
特殊函数
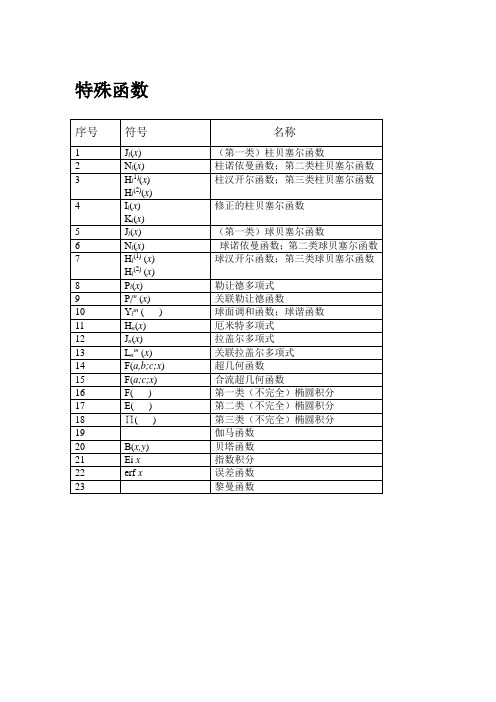
序号
符号
名称
1
Jl(x)
(第一类)柱贝塞尔函数
2
Nl(x)
柱诺依曼函数;第二类柱贝塞尔函数
3
Hl1)(x)
Hl(2)(x)
柱汉开尔函数;第三类柱贝塞尔函数
4
Il(x)
Kl(x)
修正的柱贝塞尔函数
5
Jl(x)
(第一类)球贝塞尔函数
6
Nl(x)
球诺依曼函数;第二类球贝塞尔函数
7
Hl(1)(x)
Hl(2)(x)
球汉开尔函数;第三类球贝塞尔函数
8
Pl(x)
勒让德多项式
9
Plm(x)
关联勒让德函数
10
Ylm()
球面调和函数;球谐函数
11
Hn(x)
厄米特多项式x)
关联拉盖尔多项式
14
F(a,b;c;x)
超几何函数
15
F(a;c;x)
合流超几何函数
16
F()
第一类(不完全)椭圆积分
17
E()
第二类(不完全)椭圆积分
18
∏()
第三类(不完全)椭圆积分
19
伽马函数
20
B(x,y)
贝塔函数
21
Eix
指数积分
22
erfx
误差函数
23
黎曼函数
北科大数理方程 4+ch4+勒让德(Legendre)多项式

dy dx
d ( sin
2
d (sin dx
dy dx
d dx
)
(sin
)
dx d
dx
dy dx ] d dx
2
( sin )
[(co s 1)
]
d dx
[(1 co s )
[(1 x )
dy dx
]
12
方程
d d 2 2 sin sin l ( l 1) sin m 0 d d 有限值 0 ,
2
2
0
d dr
r
(r
2
dR dr
) R r
1
2
sin
d
(sin
d d
) R r
2
sin
2
d
2
0,
2
以
R
1 d R dr (r
乘上式,得
2
dR dr
)
1
d
sin d
(sin
d d
)
1 sin
2
d
2
d
2
0,
4
1 d R dr
第四章 勒让德多项式
本章介绍另一类重要的特殊函数—勒让德函数。 勒让德函数是勒让德方程
(1 x )
2
d y dx
2
2
2x
dy dx
y 0
的解。 勒让德方程在区间[-1,1]上的有界解组成一类用途广泛的 正交函数系―勒让德多项式。 利用勒让德多项式,可以求出许多数学物理问题的解。
最新勒让德(legendre)多项式及其性质资料

勒让德(legendre )多项式及其性质一. 勒让德多项式勒让德多项式是由勒让德方程的通解推导出来的,所以我们首先引入勒让德方程,以及勒让德方程的幂级数解,勒让德方程的表达式如下:2'''(1)2(1)0x y xy n n y --++= 其中n 为非负实数 (1.1)它的幂级数解如下:12y y y =+ (1.2)其中:2241200(1)(2)(1)(3)[1]2!4!kk k n n n n n n y a x a x x ∞=+-++==-+⋅⋅⋅∑(1.3)213522110(1)(2)(1)(3)(2)(4)[]3!5!k k k n n n n n n y a xa x x x ∞++=-+--++==-++⋅⋅⋅∑ (1.4)由达朗贝尔判别法可知,当0n ≥不为整数时,这两个级数的收敛半径为1,在(1.3)式和(1.4)式中,0a 与1a 可以任意取值,它们起着任意常数的作用,显然,在区间(-1,1)内1y 和2y 都是方程(1.1)的解,所以(1.2)是(1.1)的通解。
上面(1.3)和(1.4)幂级数当||1x <时级数收敛,此外级数是发散的。
并且,我们发现,当n 取非负整数时,1y 和2y 中有一个便退化为n 次多项式,它就是方程(1.1)在闭区间[-1,1]上的有界解。
此时,适当的选定这个多项式的最高次幂系数n a ,所得的多项式称为n 阶勒让德多项式或第一类勒让德函数,记作()n P x ,下面我们来推导勒让德多项式()nP x 的表达式。
① 当n 为正偶数时1y 退化为n 次多项式。
为求得()n P x 的表达式,在1y 中我们通过n a 来表示其它各项的系数。
为此,将系数递推关系式改写成下列形式:2(2)(1)()(1)k k k k a a k n k n +++=-++ (1.5)在(1.5)式中取2kn =-,得:2(1)2(21)n n n n a a n --=-- (1.6)习惯上取n a 为 2(2)2(!)n nn a n = (1.7)于是有:2(1)2(21)(22)!2(21)2(1)!(1)(2!)n n n n n n n a n n n n n n ----=-----(22)!2(1)!(2)!nn n n -=--- (1.8)在(1.5)式中取4kn =-,并利用2n a -之值得:42(2)(3)4(23)n n n n a a n ----=--2(2)(3)(22)!(1)4(23)2(1)!(2)!n n n n n n n ---=---- 2(24)!(1)2(2!)(2)!(4)!nn n n -=--- (1.9)一般地,我们有()()222!12!()!(2)!mn m n n m a m n m n m --=--- (0,1,,2nm =⋅⋅⋅⋅⋅⋅) (1.10)我们将这些系数带入(1.3)中,并把此时的1y 记作()n P x ,可得:220(22)!()(1)2!()!(2)!nmn m n n m n m p x x m n m n m -=-=---∑ (1.11)这就是当n 为正偶数时勒让德多项式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 d ( x 1) d ( x 1) 1 2l 2 2l 2 2 (l !) dxl dxl 1 1 2 (l !)
d l 1 ( x 2 1)l d d l ( x 2 1)l 1 dxl 1 dx dxl dx
1 1 4 2 P4 ( x) (35 x 30 x 3) (35cos 4 20cos 2 9) 8 64 1 1 5 3 P5 ( x) (63x 70 x 15 x) (63cos 5 35cos 3 30cos ) 8 128
P6 ( x) 1 1 (231x 6 315 x 4 105 x 2 5) (231cos 6 126cos 4 105cos 2 50) 16 512
(4.1.2) 式的解 Y ( , ) 与半径 ,或简称为球函数.
(4.1.2)
r
无关,称为球谐函数
球谐函数方程进一步分离变量,令
Y ( , ) ( )( )
得到关于 的常微分方程
1 d d m2 sin l (l 1) 2 0 sin d d sin
称为 l 阶连带勒让德方程或缔合勒让德方程 l . 令
(4.1.3)
x cos
和
y( x) ( x)
把自变数从
换为
x ,则方程(4.1.3)可以化为下列
形式的 l 阶连带勒让德方程
d2 y dy m2 (1 x 2 ) 2 2 x l (l 1) y0 2 dx dx 1 x
勒让德多项式的图形可通过计算机仿真(如MATLAB仿真) 得到
图 4.1
计算 Pl (0) ,这应当等于多项式
Pl ( x) 的常数项.
则
如 l 为
2n 1(即为奇数)时,
P2 n 1 ( x)
只含奇 数次幂,不含常数项,所以
P2 n1 (0) 0
.
(4.1.8)
则 l 2n (即为偶数)时, P2 n ( x) 含有常数项,即 (4.1.7)中
2
(4.1.12)
,半径为
x2 1
zx
i
x x 1e
d i x 2 1ei d i( x)d
并注意到
2 1 ( x x 2 1ei )2 1 ( x 2 1)(1 ei2 ) 2 x x 2 1ei
2 x 2 1ei ( x x 2 1cos ) 2( x)( x x 2 1cos 让德多项式的积分表示
根据柯西积分公式的高阶导数,并取正方向积分有
f
(l )
l! f ( ) ( z) C ( z)l 1 d 2πi
容易证明微分表示(4.1.10)也可表示为环路积分形式
1 1 Pl ( x) 2πi 2l
C为
( 2 1)l C ( x)l 1 d
(2)模 (利用分部积分法证明)
N [Pl ( x)]2 dx
2 l 1 1
为了分部积分的方便,把上式的 Pl (x)用微分表示给出,则有
1 N 2l 2 2 (l !)
2 l
d l ( x 2 1)l d d l 1 ( x 2 1)l 1 dxl dx dxl 1 dx
(4.1.11)
z 平面上围绕 z x 点的任一闭合回路,
并取正方向.这叫作勒让德多项式的施列夫利积分表示式.
式(4.1.11)还可以进一步表为下述拉普拉斯积分.
1 π Pl ( x) ( x i 1 x 2 cos )l d π 0
【证明】 取 C 为圆周,圆心在 在 C 上有:
代入(4.1.11)得到
1 2π Pl ( x) ( x x 2 1 cos )l d 2π 0 1 π ( x i 1 x 2 cos )l d (4.1.12) π 0
这即为勒让德多项式的拉普拉斯积分表示. 从该积分还很容易看出
Pl (1) 1 Pl (1) (1)l
无关,则 m 0,即有
(4.1.4)
若所讨论的问题具有旋转轴对称性,即定解问题的解与
1 d d sin l (l 1) 0 sin d d
称为 l 阶勒让德 (legendre)方程.
(4.1.5)
同样若记
arc cos x, y( x) ( x)
1
[n(n 1) l (l 1)] Pl ( x)Pn (x)dx
1 1
因为上面等式左边的积分值为
(1 x 2 )[Pn ( x)Pl( x) Pl ( x)Pn ( x)] |1 1 0
所以当 n l 时,必然有
1
1 l
P ( x)Pn ( x)dx 0 成立.
d [(1 x 2 )Pl( x)] l (l 1)Pl ( x) 0 dx d [(1 x 2 )Pn ( x)] n(n 1)Pn ( x) 0 dx
两式相减,并在[-1,1] 区间上对x积分,得
d d 2 ( x)] Pl ( x) [(1 x 2 )Pn ( x)]}dx 1{Pn ( x) dx [(1 x )Pl dx
式(4.1.7)即为勒让德多项式的级数表示. 注意到 x cos , 故可方便地得出前几个勒让德多项式:
P0 ( x) 1
P1 ( x) x cos
1 1 2 P2 ( x) (3x 1) (3cos 2 1) 2 4 1 1 P3 ( x) (5 x3 3x) (5cos 3 3cos ) 2 8
2 l
dl 1 ( x 2 1)l dl 1 ( x 2 1)l dx l 1 1 dxl 1 dx
k l 2n
的那一项,所以
(2n)! n (2n 1)!! (4.1.9) P2 n (0) (1) 2 n (1) 2 n !n ! (2n)!! 式中记号 (2n)!! (2n)(2n 2)(2n 4)6 4 2
n
而 (2n 1)!! (2n 1)(2n 3)(2n 5)5 3 1
(2 因此, n)! (2n)!! (2n 1)!!
2、勒让德多项式的微分表示
1 dl Pl ( x) l ( x 2 1)l 2 l ! dxl
(4.1.10)
上式通常又称为勒让德多项式的罗德里格斯(Rodrigues) 表示式.
下面证明表达式 (4.1.10) 和(4.1.7)是相同的.
l 次求导过程中成为零,所以只需保留幂次 (2l 2k ) l l l k 的项,即 的项,应取 kmax [ ] ,并且注意到 2 2
dl 2l 2 k l 2k x (2l 2k )(2l 2k 1) [2l 2k (l 1)]x l dx
则上述方程也可写为下列形式的 l 阶勒让德方程
d 2 dy [(1 x ) ] l (l 1) y 0 dx dx
(4.1.6)
4.1.2 勒让德多项式的表示 1. 勒让德多项式的级数表示
我们知道:在自然边界条件下,勒让德方程的解 Pl ( x ) 为
l [ ] 2
(2l 2k )! l 2k Pl ( x) (1) l x 2 k !(l k )!(l 2k )! k 0
第四章 特殊函数(上)
——勒让德多项式 球函数
本章主要内容:勒让德多项式的来源、定 义、性质、生成与递推公式,球谐函数。
在球坐标系下对拉普拉斯方程分离变量径向部分得到 欧拉型常微分方程
d2 R dR 2 r 2r l (l 1) R 0 2 dr dr
和球谐函数方程
(4.1.1)
1 Y 1 2Y l (l 1)Y 0 sin 2 2 sin sin
n ,l
1 0
1 1
(4.2.2)
(n l ) (n l )
(4.2.3)
n l 时满足 Pn ( x)Pl ( x)dx 0 ,
称为正交性. 相等时可求出其模
Nl
2 1 l
1
2 P ( x)dx 2l 1
(l 0,1,2,)
(4.2.4)
下面给出公式(4.2.2),及其模(4.2.4)的证明 【证明】 (1)正交性 勒让德多项式必然满足勒让德方程(4.1.6),故有
【证明】 用二项式定理把
( x 2 1) l展开
l 1 2 l 1 l l! 1 2 l k k k ( x 1) l ( x ) (1) (1) l x 2l 2 k 2 l l! 2 l! k 0 (l k )!k! 2 k!(l k )! k 0
把上式对x求导 l 次.凡是幂次 (2l 2k ) l 的项在
(4.1.13)
利用拉普拉斯积分表示(4.1.12),还可以证明
Pl ( x) 1
,
(1 x 1)
x
(4.1.14)
【证明】 如从 ,则
回到原来的变量 , x
cos
1 π l Pl (cos ) cos i sin cos d π 0 1 π l Pl (cos ) cos i sin cos d π 0 l /2 1 π 2 2 2 0 cos sin cos d π l /2 1 π 1 π 2 2 0 cos sin d π 0 d 1 π
4.2 勒让德多项式的性质
