第1章基本概念
高等工程热力学第1章
t
( C) =5 t(F ) 32 9
° °
33
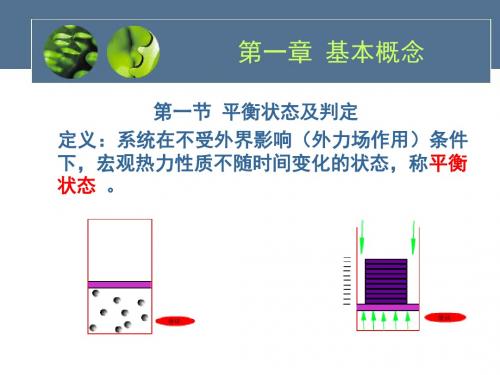
☻ 压力
绝对压力 p;
表压力 pe(pg); 真空度 pv;
p=
F A
p = pb + pe ( p > pb )
p = pb - pv ( p < pb )
动压力、静压力、滞止压力和绝对压力 ?
☻ 热力学能
Uch
G = G( p, T , n1 , n2 , , nr )
热力平衡系统
其中
是驱使第i 种组分变化的势,即化学势:
12
用A表示的化学势
改变约束条件,化学势还可有其它的表达式、但是 无论如何表示,其实质都相同:
据化学势概念,定温、定容和定压、定温系统的 平衡判据:
13
四. 稳定平衡判据
力学中平衡的稳定性
+
+
1
b2
1
C)状态参数分类: 广延量 强度量 (广延量的比性质,具有强度量特性)32
► 系统两个状态相同的充要条件: 所有状参一一对应相等 简单可压缩系两状态相同的充要条件: 两个独立的状态参数对应相等
► 基本状态参数
☻ 温度
测温的基础—热力学零定律 热力学温标和国际摄氏温标
{t } C = {T }K 273.15
δ AT ,V = 0
1
δ AT , V > 0
2
定温定压系统,平衡与稳定的条件
δ GT , p = 0
1
δ GT , p > 0
2
16
过程
不同形式能量之间的转换必须通过工质的状态变化过程才 能完成。 一切过程都是平衡被破坏的结果,工质和外界有了热的、力的 或化学的不平衡才促使工质向新的状态变化,故实际过程都是不 平衡的。
第一章 基本概念

二、代数系统的同构及性质
三、代数系统同构的意义
一、代数系统的同态及性质
定义1 设集合 M及 M 各有代数运算 o 及o, 且 ϕ是 M到 M 的一个映射 .
___ _ ___
如果 ϕ满足以下条件:对 M中任意元素 a, b, 在 ϕ之下由
a → a, b → b 总有 a o b → a o b,
n次置换
1.3
代数运算
一、代数运算的概念
近世代数的主要任务是研究各种抽象的代数系统(带有运算的集合)。 如何定义运算,先看几个我们熟悉的例子: (1)非负整数集Z上的普通加法“+”; (2)数域F上全体n阶矩阵集上的乘法。 可见运算“+” ,矩阵乘法就是个映射。 定义1 设M是一个集合.如果有一个法则,它对M中的任 意两个有次序的元素a 与b,在M中有一个惟一确定的元素 d与它们对应,则称这个法则是集合M的一个代数运算.
设ε表示集合 M的恒等变换,则对 ∀σ ∈T ( M ),有
σε ( x ) = εσ ( x ) = σ ( x ), (∀x ∈ M ),
从而 εσ = σε = σ,
在变换的乘法中,恒等变换着数1在数的普通乘法中相同的作用。
结论:设S(M)表示集合M的全体双射变换作成的集合,则
S ( M ) ⊆ T ( M ), 且变换乘法也是S ( M )的一个代数运算。
f o g, 即 f o g : X → Z,
对∀x ∈ X , ( f o g )( x ) = f [ g ( x )].
四、变换
定义:集合X 到自身的映射,叫做集合X的一个变换 . 定理3 含n个元素的任意集合共有n!个双射变换.
对有限集合的双射变换 ϕ,常用以下特殊符号表 示: L 2 n ⎞ ⎛ 1 ϕ =⎜ ⎜ ϕ (1) ϕ ( 2) L ϕ ( n) ⎟ ⎟ ⎝ ⎠
工程热力学基本知识点汇总

第一章基本概念1.基本概念热力系统:用界面将所要研究的对象与周围环境分隔开来,这种人为分隔的研究对象,称为热力系统,简称系统。
边界:分隔系统与外界的分界面,称为边界。
外界:边界以外与系统相互作用的物体,称为外界或环境。
闭口系统:没有物质穿过边界的系统称为闭口系统,也称控制质量。
开口系统:有物质流穿过边界的系统称为开口系统,又称控制体积,简称控制体,其界面称为控制界面。
绝热系统:系统与外界之间没有热量传递,称为绝热系统。
孤立系统:系统与外界之间不发生任何能量传递和物质交换,称为孤立系统。
单相系:系统中工质的物理、化学性质都均匀一致的系统称为单相系。
复相系:由两个相以上组成的系统称为复相系,如固、液、气组成的三相系统。
单元系:由一种化学成分组成的系统称为单元系。
多元系:由两种以上不同化学成分组成的系统称为多元系。
均匀系:成分和相在整个系统空间呈均匀分布的为均匀系。
非均匀系:成分和相在整个系统空间呈非均匀分布,称非均匀系。
热力状态:系统中某瞬间表现的工质热力性质的总状况,称为工质的热力状态,简称为状态。
平衡状态:系统在不受外界影响的条件下,如果宏观热力性质不随时间而变化,系统内外同时建立了热的和力的平衡,这时系统的状态称为热力平衡状态,简称为平衡状态。
状态参数:描述工质状态特性的各种物理量称为工质的状态参数。
如温度(T)、压力(P)、比容(υ)或密度(ρ)、内能(u)、焓(h)、熵(s)、自由能(f)、自由焓(g)等。
基本状态参数:在工质的状态参数中,其中温度、压力、比容或密度可以直接或间接地用仪表测量出来,称为基本状态参数。
温度:是描述系统热力平衡状况时冷热程度的物理量,其物理实质是物质内部大量微观分子热运动的强弱程度的宏观反映。
热力学第零定律:如两个物体分别和第三个物体处于热平衡,则它们彼此之间也必然处于热平衡。
压力:垂直作用于器壁单位面积上的力,称为压力,也称压强。
相对压力:相对于大气环境所测得的压力。
工程热力学第1章习题答案

第1章 基本概念1-1 为了环保,燃煤电站锅炉通常采用负压运行方式。
现采用如图1-16所示的斜管式微压计来测量炉膛内烟气的真空度,已知斜管倾角α=30º,微压计中使用密度ρ=1000kg/m 3的水,斜管中液柱的长度l =220mm ,若当地大气压p b =98.85kPa ,则烟气的绝对压力为多少Pa ?图1-16 习题1-1解:大气压力98.85kPa 98850Pa b p ==真空度3sin 1000kg/m 9.81N/kg 0.22m 0.51079.1Pa v p gl ρα==×××=烟气的绝对压力98850Pa 1079.1Pa 97770.9Pa b v p p p =−=−=1-2 利用U 形管水银压力计测量容器中气体的压力时,为了避免水银蒸发,有时需在水银柱上加一段水,如图1-17所示。
现测得水银柱高91mm ,水柱高20mm ,已知当地大气压p b =0.1MPa 。
求容器内的绝对压力为多少MPa ?图1-17 习题1-2解:容器内的压力高于大气压力,因此绝对压力b e p p p =+表压力291mmHg+20mmH O 91133.3Pa 209.81Pa 0.0123MPa e p ==×+×≈大气压力0.1MPa b p =容器内的绝对压力0.1MPa 0.0123MPa 0.1123MPa b e p p p =+=+=1-3 某容器被一刚性隔板分为两部分,在容器的不同部位安装有压力计,其中压力表B放在右侧环境中用来测量左侧气体的压力,如图1-18所示。
已知压力表B 的读数为80kPa ,压力表A 的读数0.12MPa ,且用气压表测得当地的大气压力为99kPa ,试确定表C 的读数,及容器内两部分气体的绝对压力(以kPa 表示)。
如果B 为真空表,且读数仍为80kPa ,表C 的读数又为多少?图1-18 习题1-3解:(1)容器左侧(A )的绝对压力,99kPa 120kPa 219kPa b e A p p p =+=+=A压力表B 的读数为容器左侧(A )的绝对压力A p 和容器右侧(C )的绝对压力C p 之差,因此,e B C p p p =−A ,得,219kPa 80kPa 139kPa C e B p p p =−=−=A同时,b e C p p p =+C ,可得压力表C 的读数为,139kPa 99kPa 40kPa e C p =−=(2)如果表B 为真空表,则,v B A p p p =−C ,得299kPa C p =,因此压力表C 的读数为,200kPa e C p =1-4 如图1-19所示,容器A 放在B 中,用U 形管水银压力计测量容器B 的压力,压力计的读数为L =20cm ,测量容器A 的压力表读数为0.5MPa ,已知当地大气压力p b =0.1MPa ,试求容器A 和B 的绝对压力。
核电厂辐射防护基础课后习题

第一章 基本概念1.何为碳单位,碳单位的符号和质量。
答:以一个C 12原子质量的十二分之一作为原子质量单位,记为u ,这个原子质量单位称为碳单位,kg kg u 27261066056.112/1099267.11--⨯=⨯=。
2.何为原子序数和原子质量数,用何符号表示?答:原子核中质子的数目称为原子序数,用符号Z 表示;原子核中质子数和中子数之和称为原子质量数,也称质量数,用符号A 表示。
3.用X AZ 表示原子(核)时,A 、X 和Z 各表示什么意义?答:A 是原子质量数,X 是元素符号,Z 是质子数或则是原子序数。
4.用上题的符号时,中子的数目如何确定?答:中子数Z A N -=。
5.当原子核发射一个α粒子时,从原子核中发射出哪些核子?各为多少?答:6.当原子核发射一个β粒子时,放射性原子的A 和Z 如何变化?答:A 会增加1,Z 不变。
7.当原子核发射一个γ粒子时,放射性原子的A 和Z 是否会发生变化?答:不会发生改变。
8.什么是核素和核子?同位素的天然丰度的定义。
答:通常把具有相同质子数Z 、中子数N 的一类原子(核)称为一种核素,即核素是指任一种元素的任一种同位素,也就是说原子核构成(核内中子数和质子数)完全相同的物质就是一种核素。
对于天然存在的元素,一种核素在它所属的天然元素中所占的原子百分数称为该核素的天然丰度。
9.什么是质量亏损?原子核的结合能如何表示?什么是原子核的平均结合能?答:组成原子核的Z 个质子和A-Z 个种子的质量之和与该原子核的质量之差称为原子核的质量亏损。
原子核的结合能除以该原子的质量数A 所得的商,称为平均结合能,以ε表示。
10.一个原子质量单位的物质所相应的静止质量能为多少?答:931.5MeV 。
11.在放射性衰变中,λ的意义是什么?答:λ的物理意义为单位时间内、一个核素衰变的概率。
12.样品当前的放射性活度1450Bq ,若半衰期为25min ,试问在1h 前样品的放射性活度是多少?(7656Bq )解:15006025/693.02/1=⨯==λT136001062.404-7650/1450/)(1062.44-⨯⨯--===⨯=⇒-s e e t A A λτλ13.试述放射性物质的衰变规律?说明半衰期的物理意义?衰变常数和半衰期之间的关系? 答:一定数量的某种放射性核素并不是在某一时刻突然全部衰变完,而是随时间的增加而逐渐地减少。
工程热力学和传热学课后答案(前五章)

页眉内容
对于可逆过程,都正确。
3.某封闭系统经历了一不可逆过程,系统向外界放热为10kJ,同时外界对系统作功为20kJ。
1)按热力学第一定律计算系统热力学能的变化量;
2)按热力学第二定律判断系统熵的变化(为正、为负、可正可负亦可为零)。
4.判断是非(对画,错画×)
1)在任何情况下,对工质加热,其熵必增加。()
2.下列说法是否正确,为什么?
1)熵增大的过程为不可逆过程;
只适用于孤立系统
2)工质经不可逆循环,S0;
S =0
3)可逆绝热过程为定熵过程,定熵过程就是可逆绝热过程;
定熵过程就是工质状态沿可逆绝热线变化的过程
4)加热过程,熵一定增大;放热过程,熵一定减小。
根据ds≥△q/T,前半句绝对正确,后半句未必,比如摩擦导致工质温度升高的放热过程。
w123>w143
14
谁大谁小?又如2和3在同一条等温线上呢?
所以
P
v
图4-2
2
2->3为绝热膨胀过程,内能下降。所以
u2>u3。
4.讨论1<n<k的多变膨胀过程中绝气热体线温度的变化以及气体与外界热传递的方向,并用热力学第一
(3)绝热系统。
图
1-1
5.判断下列过程中那些是不可逆的,并扼要说明不可逆原因。
(1)在大气压力为0.1013MPa时,将两块0℃的冰互相缓慢摩擦,使之化为0℃的水。
耗散效应
(2)在大气压力为0.1013MPa时,用(0+dt)℃的热源(dt→0)给0℃的冰加热使之变为0℃的水。
可逆
(3)一定质量的空气在不导热的气缸中被活塞缓慢地压缩(不计摩擦)。
800kJ。从状态2到状态3是一个定压的压缩过程,压力为p=400kPa,气体向外散热450kJ。并且已
第一章 热力学基本概念
工程热力学与传热学第一章基本概念典型问题分析典型问题一.基本概念分析1闭口系统具有恒定的质量,但具有恒定质量的系统不一定就是闭口系统。
2孤立系统一定是闭口的,反之则不然。
3孤立系统一定是绝热系统,但绝热系统不一定都是孤立的。
4孤立系统的热力学状态不能发生变化。
5平衡状态的系统不一定是均匀的,均匀系统则一定处于平衡状态。
6摄氏温度的零点相当于热力学温度的273.15K。
7只有绝对压力才能表示工质所处的状态,才是状态参数。
8只有平衡状态,才能用状态参数坐标图上的一点来表示。
9非平衡状态,因为没有确定的状态参数,无法在状态参数坐标图中表示。
10不平衡过程,一定是不可逆过程;11不可逆过程就是指工质不能恢复原来状态的过程;12一个可逆过程必须同时也是一个准平衡过程,但准平衡过程不一定是可逆的。
13实际过程都是不可逆过程。
14功可以全部转变为热,但热不能全部转变为热15质量相同的物体A和B,若T A >T B,则物体A具有的热量比物体B多。
二.计算题分析1测得容器内气体的表压力为0.25MPa,当地大气压为755mmHg,求容器内气体的绝对压力p,并分别用(1)MPa(兆帕);(2)bar(巴);(3)atm(物理大气压);(4)at(工程大气压)表示。
2某种气体工质从状态1(p1,V1)可逆地膨胀到状态2。
膨胀过程中:(1)工质的压力服从p=a-bV,其中a,b为常数;(2)工质的pV保持恒定为p1V1。
试分别求两过程中气体的膨胀功。
3利用体积为2m3的储气罐中的压缩空气给气球充气,开始时气球内完全没有气体,呈扁平状,可忽略其内部容积。
设气球弹力可忽略不计,充气过程中气体温度维持不变,大气压力为0.9 ╳105Pa。
为使气球充到2m3,问气罐内气体最低初压力及气体所作的功是多少?已知空气满足状态方程式pV=mR g T。
分析解答一. 基本概念分析解答1 √;2 √;3 √;4 ╳;5 √;6 √;7 √;8 √;9 √;10 √;11 ╳;12 √;13 √;14 ╳;15 ╳;二. 计算题分析解答1 解:依据: Pa Pa Pa p Pa mmHg p p p b e 66107305.04322.1337551025.04332.1331,⨯=⨯+⨯==+=单位换算:at Pa Pa atm PaPa bar Pa Pa MPa PaPa 7575.35.06698107305.0)4(7460.3325101107305.0)3(057.310107305.0)2(7305.010107305.01665666=⨯=⨯=⨯=⨯)( 2 解:过程为可逆过程: 1211212121212221122121ln )2()(2)()(1V V V p V dV pV pdV W V V b V V a dV bV a pdV W ===---=-==⎰⎰⎰⎰--)( 分析:在上述两过程中,系统的初,终态相同,但中间途径不同,因而气体的膨胀功也不同。
《理论力学》第一章基本概念及基本原理
第一章 基本概念及基本原理[习题1-1] 支座受力F ,已知kN F 10=,方向如图所示, 求力沿y x ,轴及沿'',y x 轴分解的结果,并求力F 在各轴上的投影.解:(1)F 沿y x ,轴分解的结果把F 沿y x ,轴分解成两个分力,如图所示. →→→→=⨯==i i i F F x 66.8866.01030cos 0)(kN →→→→=⨯==j j j F F y 55.01030sin 0)(kN (2)F 沿'',y x 轴分解的结果把F 沿'',y x 轴分解成两个分力,如图所示. 由图可知,力三角形是等腰三角形.故:→→→==''10'i i F F x )(kN→→→-=⨯-=''018.575cos 102'j j F y )(kN (3) F 在y x ,轴上的投影)(66.8866.01030cos 0kN F F x =⨯==)(55.01030sin 0kN F F y =⨯== (4) F 在'',y x 轴上的投影)(66.8866.01030cos 0'kN F F x =⨯==)(59.275cos 1075cos 00'kN F F y -=-=-=[习题1-2] 已知N F 1001=,N F 502=,N F 603=N F 804=,各力方向如图所示,试分别求各力在x 轴y 轴上的投影. 解:)(6.86866.010030cos 011N F F x =⨯==)(505.010030sin 011N F F y =⨯==)(305350cos 222N F F x =⨯==α力沿x,y 轴的分解图力沿x ’,y ’轴的分解图力沿x ’,y ’轴的投影图xF yFy 'x F ')(405450sin 222N F F y -=⨯-=-=α 0060cos 333=⨯==αF F x)(60160sin 333N F F y =⨯==α)(57.56135cos 80cos 0444N F F x -===α)(57.56135sin 80sin 0444N F F y ===α[习题1-3] 计算图中321,,F F F 三个力分别在z y x ,,轴上的投影.已知kN F 21=,kN F 12= , kN F 33=. 解:)(2.16.025311kN F F x -=⨯-=⨯-= )(6.18.025411kN F F y =⨯=⨯=01=z F)(424.05345sin 1cos sin 02222kN F F x =⨯⨯==θγ )(566.05445sin 1sin sin 02222kN F F y=⨯⨯==θγ)(707.045cos 1cos 0222kN F F z =⨯==γ03=x F03=y F)(333kN F F z ==[习题1-4] 已知kN F T 10=,求T F 分别在z y x ,,轴上的投影. 解:(591.75353510sin 22222F F T Txy =+++⨯==γ)(51.6355591.7cos 22kN F F Txy Tx =+⨯==θ题1-2图)3,)0,)(91.3353591.7sin 22kN F F Txy Ty =+⨯==θ)(51.6535510cos 222kN F F T Tz -=++⨯-=-=γ[习题1-5] 力F 沿正六面体的对角线AB 作用,kN F 100=,求F 在ON 上的投影. 解:如图所示,F 在AC 线上的投影为:)(345.88400300400400400100cos 22222kN CAB F F F OB AC =+++⨯===5.0400200tan ==NOD 057.265.0arctan ==NOD 00043.1857.2645=-=BONF 在ON 线上的投影为:)(811.8343.18cos 345.88cos 0kN BON F F O B O N ===[习题1-6] 已知N F 10=,其作用线通过A(4,2,0),B(1,4,3)两点,如图所示.试求力F 在沿CB 的T 轴上的投影. 解: 61.313)42()14(22==-+-=AD69.413361.322==+=AB 2361.322=-=DGF 在AD 上的投影为:M)(697.769.461.310cos N BAD F F AD =⨯== )(40.669.4310sin N BAD F F z =⨯==)(264.461.32697.7cos N ADG F F AD y =⨯==)(396.661.33697.7sin N ADG F F AD x =⨯==F 在T 轴上的投影为:)(251.75340.654264.4cos cos kN ECB F BCD F F z y T =⨯+⨯=+= [习题1-7] 图中圆轮在力F 和矩为M 的力偶作用下保持平衡,这是否说明一个力可与一个力偶平衡? 解:图中圆轮在力F 和矩为M 的力偶作用下保持平衡,这不能说明一个力可与一个力偶平衡.因为轮子的圆心处 有支座,该支座反力R 与F 构成一力偶,力偶矩),(F R M 与M 等值,共面,反向,故圆轮保持平衡.[习题1-8] 试求图示的力F 对A 点之矩,已知m r 2.01=m r 5.02=,N F 300=.010012030cos 60sin )30sin (60cos )(r F r r F F M A ⋅+--=)(15232.023300)5.02.05.0(5.0300)(m N F M A ⋅-=⨯⨯⨯+⨯-⨯-= [习题1-9] 试求图示绳子张力T F 对A 点及对B 点的矩.已知kN F T 10=,m l 2=,m R 5.0=,030=α.解:)(530sin 10sin 0kN F F T Tx ===α)(66.830cos 10cos 0kN F F T Ty ===α )(732.1866.0260sin 0m l OC =⨯==)(15.0260cos 0m l AC =⨯==)()()(Ty A Tx A T A F M F M F M +=)30cos 5.01(66.8)30sin 5.0732.1(500+⨯+-⨯-=)(5m kN ⋅=)()()(Ty B Tx B T B F M F M F M +=)30cos 5.01(66.8)30sin 5.0732.1(500-⨯--⨯-=)(320.12m kN ⋅-=[习题1-10] 已矩正六面体的边长为c b a ,,,沿AC 作用一力F ,试求力F 对O 点的矩矢量表达式. 解:zy xF F F c bak j iF M →→→=)(0式中,2222222222cos cos c b a Fa b a a c b a b a F F F x ++-=+⋅+++⋅-=⋅-=θγ2222222222sin cos cb a Fb ba b cb a b a F F F y ++-=+⋅+++⋅-=⋅-=θγ222222sin cb a Fc cb ac F F F z ++=++⋅==γ故cb ac b ak j i c b a FF M --++=→→→2220)(cc bak j i c b a F200222→→→++=baj ic c b a F→→⋅++=2222)(2222→→-++=j a i b c b a cF[习题1-11] 钢绳AB 中的张力kN F T 10=.写出该张力T F 对O 点的矩的矢量表达式.解:2)21()01(22=-+-=BC2318)04()12()10(222==-+-+-=ABzy xF F F k j iF M 42)(0→→→=式中,)(357.22123210cos cos kN F F T Tx =⋅⋅=⋅=θγ )(357.22123210sin cos kN F F T Ty -=⋅⋅-=⋅-=θγ)(428.923410sin kN F F T Tz -=⋅-=-=γ故428.9357.2357.2420)(0--=→→→k j i F M 357.2357.24428.9357.22---=→→→→jiki)(357.24)357.2428.9(2→→→→--⨯---=j i k i →→→-+-=k j i 714.4428.9428.9[习题1-12] 已知力→→→→+-=k j i F 32,其作用点的位置矢→→→→++=k j i r A 423,求力F 对位置矢为→→→→++=k j i r B 的一点B 的矩(力以N 计,长度m 以计).A解:→→→→→⨯-=⨯=F r r F r F M B A AB B )()(式中,→→→→++=k j i r A 423,→→→→++=k j i r B ,=-→→)(B A r r →→→++k j i 312 →→→→+-=k j i F 32故, =)(F M B ⨯++→→→)312(k j i )32(→→→+-k j i=-=→→→132312k j i=--→→→240312k j i 23522---→→→→k k j i 5222---=→→→k j i)425(2→→→+---=k j i→→→-+=k j i 8410 )(m N ⋅[习题1-13] 工人启闭闸门时,为了省力,常常用一根杆子插入手轮中,并在杆的一端C 施加力,以转动手轮.设手轮直径m AB 6.0=,AC 轩长m l 2.1=,在C 端用N F C 100=的力能将闸门开启,若不借用杆子而直接在手轮A,B 施加力偶),('F F ,问F 至少应多大才能开启闸门? 解:支座O 反力O R 与C F 构成一力偶),(0C F R 若要闸门能打开,则),('F F 与),(0C F R 必须 等效,即它们的力偶矩相等:)3.02.1(1006.0-⨯=⨯F )(150N F =[习题1-14] 作下列指定物体的示力图.物体重量,除图上已注明者外,均略去不计.假设接触处都是光滑的.。
第1章 习题提示和答案
中液柱长度l=200mm。当地大气压力
p v
=
745mmHg
。ห้องสมุดไป่ตู้烟气的真空
度(以mmH2O表示)及绝对压力(以Pa表示)。
图 1-25 斜管压力计
提示和答案: 倾斜式压力计上读数即烟气的真空度 pv = l sin αρ g = 80 × 9.81Pa ,故
pv = 80mmH2O ;烟气绝对压力
p = p − p = 10048.3mmH O = 0.9857 ×105 Pa 。
1−16 某种气体在气缸中进行一缓慢膨胀过程。其体积由 0.1m3增加到 0.25 m3。过程中气
体压力循{ p} MPa
= 0.24 − 0.4{V }m3
变化。若过程中气缸与活塞的摩擦保持为
1200
N;当地大
气压力为 0.1MPa;气缸截面积为 0.1m2,试求:(1)气体所作的膨胀功W ;(2)系统输出的
1-12 气缸中密封有空气,初态为 p1 = 0.2MPa,V1 = 0.4m3 ,缓慢胀到V2 = 0.8m3 。(1)
过程中
pV
保持不变;(2)过程中气体先循{ p} MPa
=
0.4
−
0.5
{V
} m
3
膨胀到 Vm
=
0.6m3 ,再维
2
第一章 基本概念
持压力不变,膨胀到V2 = 0.8m3 。分别求出两过程中气体作出的膨胀功。
v1
v3
p2
p3 RgT3
= Ta ;同理 Tb
v5 v4
=
Ta Tb
,即 v2 v1
=
v5 v4
, w12
=
w45 。表明 1kg 工质在 1-2 和
西安交通大学工程热力学 第1章 基本概念及定义
第1-2节 热力系统
西安交通大学热与流体中心
二、热力系统分类
——根据系统与外界物质交换、热量交换的情况
(3)绝热系统:系统与外界无热量交换
W
Q
冷源
把冷源包括在内的绝热系统 第一章 基本概念及定义 第1-2节 热力系统
西安交通大学热与流体中心
二、热力系统分类
——根据系统与外界物质交换、热量交换的情况
第一章 基本概念及定义
第1-3节 工质的热力学状态及其基本状态参数
西安交通大学热与流体中心
三、温度
温度计
第一章 基本概念及定义
第1-3节 工质的热力学状态及其基本状态参数
西安交通大学热与流体中心
三、温度
温度T 的一般定义 传统:冷热程度的度量。感觉,导热,热容量
微观:衡量分子平均动能的量度
T 0.5 m w 2
第一章 基本概念及定义
工程热力学
西安交通大学热流中心 吴江涛
Email:jtwu@
西安交通大学热与流体中心
目录
§ 1-1 热力系统
§ 1-2 工质的热力学状态及其基本状态参数 § 1-3 平衡状态、平衡方程、坐标图 § 1-4 工质的状态变化过程
§ 1-5 过程功和热量
(4)孤立系统:系统与外界无物质、无能量交换
孤立系统的 一切相互作用都
发生系统内部。
第一章 基本概念及定义
第1-2节 热力系统
西安交通大学热与流体中心
二、热力系统分类
按物质交换
闭口系:与外界无物质交换的系统 开口系:与外界有物质交换的系统
CM CV
按能量交换 简单可压缩系:热力系与外界只有热量和可逆体积变化 功的交换。 孤立系:与外界无任何能量和物质交换的热力系。 绝热系:与外界无热量交换的系统。 热 源:与外界仅有热量的交换,且有限热量的交换 不引起系统温度变化的热力系统。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xs xi
( x xi ) ti
x xi t ( x)(F) 32 180 xs xi
依赖于实际测温物质,测温工质不 同结果会不同,这是经验温标
热力学温标
根据卡诺定理有:
T1 WA Q1 A Q2 T2 Q2 WB B Q3 T3 Q3 C Q1 WC
Q1 (t1 , t 2 ) Q2
B
毛细管
L
盛气小泡 A
水银柱
定容式气体温计示意图
理想气体温标 理想气体温标
根据理想气体温度计的原理,在1标准大气压下经过冰点(角 标i)和沸点(角标s)标定后,其压力和温度关系如下:
t ti p pi ts ti ps pi
p / pi 1 t ti ts ti p s / p i 1
-270-1100
-200~750(液) -30~600(固)
接触式测温
电阻温度计 热电偶 光学温度计
电阻 热电动势 辐射强度
-200~800
-200~1300 -50-2000
非接触式测温
一等标准铂电阻温度计其精度可达0.001℃ 电厂过热器气温等一般采用热电偶测温
温标
温标:为量度物体温度而赋予温度的数值。
需要有一种简单、容易再现,便于使用的二级标 准温度计 。
国际温标及其发展
国际计量委员会于1968年开始采用国际实用温标(IPTS68),以取代早期的温度标度。
1990年开始使用1990年国际温标,以取代1968年国际实用 温标(IPTS-68)。
1990年国际温标明确规定了:(1)容易复现的固定点的 气体温标温度和用以检定仪器的二级参考温度;(2)二 级温度标准的仪器仪表的度数用于根据固定点进行内插的 公式。为了完整起见,这是列出了规定的热力学温标固定 温度点。(ITS-90)将适用于温度测量和内插的方法概括 为四个分区。
3kBT mv
2
式中:T是热力学温度,K; kB=1.38054×10-23 J/K,波尔兹曼常 数; v为分子移动的均方根速度。
事实上确定分子的平均速度是非常困难的; 温度还需一个更严谨的定义,这就有赖于热力 学第零定律。
热力学第零定律
热力学第零定律:当两个系统各自与第三个系统 处于热平衡时,则这两个系统彼此也处于热平衡。
外推ptr→0时不同气体对目标物体温度的测量的一致性,并 获得温度测量值。下式定义理想气体温标(开氏):
T ( p ) 273.16 lim
ptr 0
p (V 为常数) ptr
温标
热力学温标、摄氏温标、朗肯温标、和华氏温标的关系
热力学温度
1854 年 , 开 尔 文 提 议 将 水 三 相 点 (triple point) 的 温 度 , Ttr=273.16K,作为热力学温度的基准,于 1954年被第十届国 际计量大会采纳。同时用K表示理想气体绝对温标的单位。 受水中氢氧同位素的影响,不同三相点瓶结果差异达50 μK。 目前国际上通过波尔兹曼常数kB来确定热力学温度。
3到5K 13.8033K ≈17K ≈20.3K 24.5561K 54.3584K 83.8058K 234.3156K 273.16K 302.9146K 429.7485K 505.078K 692.677K 933.473K 1234.93K 1337.33K 1357.77K
国际温标及其发展 ITS-90温标
3He和4He
e-H2 e-H2(或He) e-H2(或He) Ne O2 Ar Hg H2O Ga In Sn Zn Al Ag Au Cu
VP TP VP(或CVGT) VP(或CVGT) TP TP TP TP TP MP FP FP FP FP FP FP FP
p T Ttr p tr
p T ( p) 273 .16 lim (K ) p 0 ptr
tr
理想气体温标
气体的维里方程为:
T
2 3 PV RT (1 B p C p D p
)
气体A
气体B
如左图所示,所有气体 压力当p→0时,其PV性质 都趋于一相同的特性。 特别是定容式温度计内 装的气体量趋于零时,所 有气体的温度指示趋于同 一数值,这说明理想气体 定容式温度计与气体性质 无关。
当p→0,而p/pi→const,t→tc,此时pi<p<ps。 当p→0且p/pi →0时,表示p<pi ,此时测量的是低于冰点的 温度范围(实际p→0与p/pi →0意味着测量绝对零度的温度 ), t→t0 =-273.15 ℃。上式变换有
t 273.15 273.15 p pi
T 273.15 p pi
由此可以断定:
(t 2 , t 3 )
三个恒温热源间的卡诺循环
QL f (t L ) QH f (t H )
QL TL QH TH
直接用函数f(t)=T作为温标
理想气体温标
气体压力p→0时,气体呈现出理想气体特性,利 用理想气体定压下体积随温度变化的特性或定容 下压力随温度变化的特性,作为度量温度变化的 标准,这种温标称为理想气体温标。 理想气体温标是一种经验温标; 气体温度计有定容式和定压式,定容式温度计的 测量原理:
C物体
衡 平 热 平 热
衡
一定是热平 衡的
A物体
B物体
热力学第零定律 温度的热力学定义:处于同一热平衡状态的各个 热力系统,必定有某一宏观特征彼此相同,用于 描述此宏观特征的物理量为温度。 热力学第零定律为温度测量提供了科学基础:即 被测物体与温度计处于热平衡时,就可以从温度 计的读数确定被测物体的温度值。
摄氏温标:将标准大气压下水的冰点和沸点之间 的温度等分为100份,并以冰点作为零点。
华氏温标:水的冰点与沸点分别定义为 32 ℉ 和 212℉。 ts ti
t
t 100 80 60 A 40 20 0 测温参数x C A-任意的 B-线性的 C-抛物线的
B
x xi t ( x)(C) 100 xs xi
因此:
t ti
ts ti p 1 ps / pi 1 pi
重复上面的温度测量过程,不同的是需从盛气小泡中取出 一部分气体,使小泡内的压力进一步降低,更加接近理想气 体的性质,分别得出更低压力下的p、t、ti、 pi、 ts、ps。
理想气体温标
t、ti、ts不变,ps /pi和p/pi同步变化,t=f(p/pi)。 随着小泡内的气体不断被取走当p→0时,pi→0与ps→0。 根据前述理想气体一致性特性,此时虽然pi→0与ps→0,但 冰点和沸点的温度对所有气体都趋于ti与ts ,而任意测量的温 度特性对应的温度应该有 p→0、 t→tc的特性,并且不论使用 任何气体,在p→0、 pi →0、ps →0都有t→tc ,这就是A、B、 C三种气体当小泡内测量压力 p→0时趋于一致性的结果,即 理想气体温度计与气体性质无关。 存在一个普遍情况,经多次改变定容式气体温度计内的气 体量,使得冰点和沸点时气体温度计的读数pi与ps不断减小, 达到pi→0与ps →0的目的。结果发现即使pi →0与ps →0时,其 比值ps / pi总是为一固定数值不变: ps / pi =1.3661
第一章 基础概念
什么是工质?
定义:实现能量转化的媒介物质 制冷工程中又称为制冷剂
对工质的要求:
1)膨胀性 3)热容量 5)对环境友善
2)流动性 4)稳定性,安全性 6)价廉,易大量获取
物质三态中气态最适宜作为工力学研究对象的有限 物质系统 外界:系统以外的所有物质 边界(界面):系统与外界的分界面
国际温标及其发展 ITS-90温标
从0.65到5.0K根据 3He和 4He的蒸气压测量,后者又进一步 分为两段。每一段用 12 项多项式 (polynomial) 表示蒸气压与 温度的关系。 从 3.0 到 24.5561K 用氦气定容气体温度计测量,该温度计 3 到 5K 用氦气的蒸气压测定一个温度点、一个氢气的三相点 温度和一个氖气的三相点温度,共三个固定点标定。 从 13.8033 到 1234.93 K按照技术规范用在表中的固定点标 定的标准铂电阻温度计测量,并在四个子分区内用状态方程 作进一步校正,也可更加细分这些分区。 高于 1234.93K 通过测量可见光谱的辐射强度,与 Ag , Au 或 Cu 凝固点同波长辐射强度比较,并且根据普朗克黑体辐 射方程确定的温度值。
气体C
ptr
理想气体温标
将气体温度计的盛气小泡浸没在大 气压下的饱和水与饱和蒸汽的混合物 中,当温度改变时通过改变水银柱内 水银量 ( 增加或减少 ) ,控制盛气小泡 的气体体积保持不变,记录下该固定 点温度ts与此时的压力ps; 再把盛气小泡浸没在大气压下冰水 混合物中,保持气体容积不变,记录 下该固定点温度ti和小泡内压力pi; 然后再用温度计测量某一目标的温 度,将温度计盛气小泡与目标接触, 记录下温度t与小泡内的压力p。
理想气体温标
国际温标规定,以水的三相点作为绝对温标的基准温度点。 用单固定点作为温标基准的同时,必须要给出温标的单位才 能最终确定温标具体数值。水的三相点的温度Ttr=273.16,水 的三相点 (固、液、汽三相共存 ) 的压力为 ptr,则定容式气体 温度计的读数用下式表示:
T p Ttr ptr p p T Ttr 273.16 ptr ptr
系统、外界和边界
划分热力系统举例
1-锅炉;2-汽轮机;3-凝汽器;4-水泵 a)以锅炉为热力系统; b)以汽轮机为热力系统; c)以整个蒸汽动力装置为热力系统
热力系统分类
以系统与外界关系划分:
有 开口系 非绝热系 非孤立系 无 闭口系 绝热系 孤立系
有无质量传递 有无热量传递 有无能量、物质传递
