线性代数方程组中的预处理共轭梯度法

共轭梯度法

Hesteness和Stiefel于1952年为解线性方程组而提出
•基本思想:把共轭性与最速下降法相结合,利用已知点处的梯度构造一组共轭方向,并沿着这组方向进行搜索,求出目标函数的极小点
4.4共轭梯度法
先讨论对于二次凸函数的共轭梯度法,考虑问题
min f (x) 1 xT Ax bT x c
3, giT d (i) giT gi (蕴涵d (i) 0)
证明: 显然m1,下用归纳法(对i)证之.
当i 1时,由于d (1) g1,从而3)成立,对i 2时, 关系1)和2)成立,从而3)也成立.
4.4共轭梯度法
设对某个i<m,这些关系均成立,我们证明对于i+1
也成立.先证2),
因此
2 / 3 1 5/ 9
d (2)

1/ 1
3

1 9

2 0

5/9 1

从x(2)出发,沿方向d (2)进行搜索,求步长2,使满足 :
f
( x (1)

2d (1) )

min
0
f
(x(2)

d (2))

2 0

4.4共轭梯度法
显然, d (1)不是目标函数在x(1)处的最速下降方向.
下面,我们用FR法构造两个搜索方向.
从x(1)出发,沿方向d (1)进行搜索,求步长1,使满足 :
f
( x (1)
1d (1) )

min
0
f
( x (1)

d (1) )
得1 2 3
A正定,故x是f(x)的极小值点.

共轭梯度法原理

共轭梯度法原理共轭梯度法是线性代数中一种求解稀疏矩阵下的大规模线性方程组的方法。

它的优点是它具有迭代次数小的特点，同时也能得到比较准确的解。

共轭梯度法基于梯度下降法，但是避免了梯度下降法的缺点。

梯度下降法每一次迭代都需计算整个向量的梯度，这在高纬度数据中非常复杂，同时使用步长较大时又容易产生来回震荡的现象。

共轭梯度法的优点是在每一次迭代都会寻找一个与上次方向不同的方向，这点可以消除梯度下降法的缺陷。

令A为若干个线性矩阵的乘积，如果我们要解矩阵方程Ax=b，其中b是已知向量，求解的x向量是未知向量。

首先，我们可以用梯度下降法求出一个初值向量x0，称之为迭代初始值。

然后，我们可以利用高斯打乘法和高斯消元得到向量P，并设向量R0=Ax0-b，然后再设P逆矩阵为Pt。

共轭梯度法迭代的主要步骤如下：1. 根据目标函数和梯度函数确定初值x0；2. 初始化残差向量r0=b-Ax0，并设置迭代数k=0；3. 设置搜索方向向量p0=r0；4. 使用一维搜索方法（如Armijo步长准则）寻找最优步长αk；5. 将搜索方向向量移动到新的位置：xk+1=xk+αkp，计算新的残差rk+1=rk+αkAp；6. 如果rk+1=0或者迭代次数已达到设定值，则停止迭代；否则：7. 确定下一个搜索方向pk+1，并重复步骤4-6直到满足收敛条件。

共轭梯度法迭代的优点是每一步都在原解空间的一个线性子空间中求解，因此不需要保存全部解向量，从而大大减少了计算量和存储空间，特别适用于高纬度的线性方程组的求解。

在参数优化、图像处理和物理模拟等领域中广泛应用。

在参数优化中，共轭梯度法可以加速大规模函数的梯度计算，从而加快参数搜索的速度；在图像处理中，共轭梯度法常用于求解稀疏线性系统，例如图像压缩、图像去噪和图像恢复等；在物理模拟中，共轭梯度法可以用于求解偏微分方程组、流体力学问题和计算机视觉等领域。

3_共轭梯度法

共轭梯度法
基本思想
CG的基本思想是把共轭性与最速下降法相结合，利用已知点处的梯度构造一组共轭方向，并沿着此组方向进行搜索，求出目标函数的极小点。
d k f ( xk ) k 1d k 1 , k 1,2,..., n 1.
定义--共共轭梯度法的形式 (A) 正定二次函数的无约束最优化问题的共轭梯度法形式
共轭方向法和共轭梯度法
问题1:
如何建立有效的算法？
从二次模型到一般模型.
问题2: 什么样的算法有效呢？二次终止性.
简介
共轭方向法和共轭梯度法
共轭梯度法是介于最速下降法与牛顿法之间的一个方法，它仅需利用一阶导数信息，但克服了最速下降法收敛慢的缺点，又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点，共轭梯度法不仅是解决大型线性方程组最有用的方法之一，也是解大型非线性最优化最有效的算法之一.
注意
由于Rn中共扼方向最多有 n 个，因此在用上述二种方法求解目标函数为非二次函数的无约束最优化问题(7.1.1)时，在 n 步之后构造的搜索方向不再是共轭的，从而降低了收敛速度克服的办法是重设初始点，即把经过 n 次迭代得到的 xn 作为初始点重新迭代．
算法步骤—FR共轭梯度法
共轭梯度法
Step1: Step2: Step3: Step4: Step5: Step6: Step7:
注：若 G I ,则
因此, 共轭是正交的推广．定义--共轭方向法
是正交的，
共轭方向法
性质
特例
n
共轭方向法
算法步骤
Step1: Step2: Step3: Step4:
Step5:
共轭方向法
特例
注

——共轭梯度法ppt课件

r ( k 1 ) , r ( k 1 ) r ( k ) kr ( k ) k 1 p ( k 1 ) , A p ( k )
1 r(k1),r(k1)
k
r(k),Ap(k)
r(k1), r(k1)
r(k), r(k)
共轭梯度法
算法：(共轭梯度法 )
(1) (x) 的梯度为：
(x) x 1, Rn 和 R，有
(x y ) 1 A (x y ),x y b ,x y 2 2A y,y(A xb,y)(x) 2
(3) 令 x*=A-1b，那么有
( x ) 1 b T A 1 b b T A 1 b 1 b T A 1 b 1 A x ,x
计算方法
第六章线性方程组的迭代解法
—— 共轭梯度法
本讲内容
共轭梯度法
最速下降法共轭梯度法共轭梯度法的收敛性分析
等价问题
思索线性方程组：Ax = b ，其中 A 对称正定作二次泛函 (x): Rn R
(x )1(A x ,x ) (b ,x )1x T A xx T b
2
2
(x) 具有以下性质：
证明：板书
共轭梯度法
k 与 k 的计算
k r ( k ) , p ( k ) p ( k ) , A p ( k ) r ( k ) , r ( k ) p ( k ) , A p ( k )
k r ( k 1 ) ,A p ( k ) p ( k ) ,A p ( k )
共轭梯度法
详细作法：令 p(0) = r(0) ，设 x(k) 曾经求得，那么 x(k+1) 由下面的公式确定：
x(k1)x(k)kp(k)
其中
p(k)r(k)k1p(k1)

计算方法——共轭梯度法求解线性方程组

x( k 1) x( k ) k d ( k )
(2)
(k)
共轭梯度法中关键的两点是迭代格式(2)中最佳步长k 和搜索方向 d
(k) (k)
的确定。其
中k 可以通过一元函数f(x +d )的极小化来求得，其表达式为公式(3)；取 d (0) = r(0) = b-Ax(0)，则 d(k+1) = r(k+1) +kd(k)，要求 d(k+1)满足 (d(k+1) , Ad(k)) = 0，可得k 的表达式(4)。
计算方法上机报告
计算方法上机报告
1 共轭梯度法求解线性方程组
1.1 算法原理及程序框图当线性方程组 Ax = b 的系数矩阵 A 是对称正定矩阵是，可以采用共轭梯度法对该方程组进行求解，可以证明，式(1)所示的 n 元二次函数 1 f ( x ) x T Ax bT x (1) 2 取得极小值点 x*是方程 Ax = b 的解。共轭梯度法是把求解线性方程组的问题转化为求解一个与之等价的二次函数极小化的问题。从任意给定的初始点出发，沿一组关于矩阵 A 的共轭方向进行线性搜索，在无舍入误差的假定下，最多迭代 n 次（其中 n 为矩阵 A 的阶数），就可求得二次函数的极小点，也就求得线性方程组 Ax = b 的解。其迭代格式为公式(2)。
4
1 1
1 0 ，b 2 1 0 1 1 2
计算方法上机报告
矩阵 A 的阶数取 200 进行求解。由于该线性方程组的系数矩阵阶数比较大，而且具有一定的规律，因此首先用 matlab 编程将系数矩阵、右端项以及阶数保存在 D 盘根目录的三个文件中（生成系数矩阵，右端项以及阶数的程序见附录 2），然后运行共轭梯度法程序进行方程组的求解。最终的运行结果为图 4 和图 5。程序运行之后 D 盘根目录下生成的文件如图 6 所示。

共轭梯度法求解线性方程组

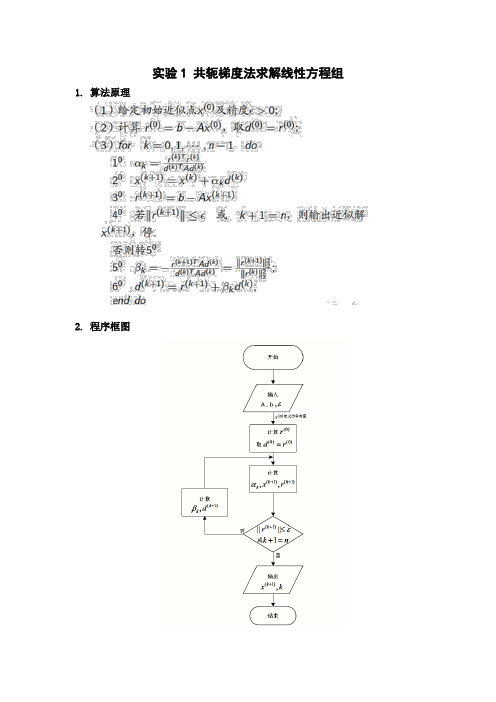
实验1 共轭梯度法求解线性方程组1.算法原理2.程序框图3.程序使用说明。

本程序使用MATLAB来求解线性方程组Ax b源程序文件“gongetidu1.m”为共轭梯度法源程序，x为方程组的解，k为迭代次数，A为方程组的系数矩阵，b为方程组的右端项，ep为精度。

定义A, b，ep后，在命令窗口输入[x,k] = gongetidu1(A,b,ep)，回车后即可算出方程组的解和迭代次数。

源程序文件“gongetidu2.m”为共轭梯度算例3.2中构造A，b矩阵的程序。

定义阶数n的数值后，在命令窗口输入[A,b] = gongetidu2(n)即可算出A, b矩阵。

4.算例计算结果此算例为课本113页计算实习3.2.首先，设定MATLAB的数值格式为“long”。

当n=100时，在命令窗口中输入“[A,b]=gongetidu2(100)”，回车后可得到A 和b的矩阵；假设精度ep = 10-3，然后在命令窗口输入“[x,k] = gongetidu1(A,b,10^-3)”即可算出方程组的解x和迭代次数k。

x=( 0.999999999999988,0.999999999999995,1.000000000000009，···0.9999 99999999997,0.999999999999998 )T（x向量一共有100个元素）k=49.同理，可以算出n=200,400的结果。

n=200时，同样假设精度ep = 10-3，结果为：x=( 0.999999999999974,1.000000000000023,0.999999999999935,···1.000000 000000029, 0.999999999999987)T （x向量一共有200个元素）k=99.n=400时，同样假设精度ep = 10-3，结果为：x=( 1.000000000000017,0.999999999999846,1.000000000000039,···0.99999999 9999881,1.000000000000062)T （x向量一共有400个元素）k=199。

利用共轭梯度法求解线性方程组

利用共轭梯度法求解线性方程组翟莹1012205052在自然科学和工程技术中很多问题的解决常常归结为解线性方程组，而这些方程组的系数矩阵大致可分为两种:低阶稠密矩阵和大型稀疏矩阵。

而求解方程组的方法通常为直接法和迭代法。

直接法用于较低阶方程组的求解，效率较高；迭代法更适用于高阶方程组的求解，常用的经典迭代法有高斯-赛德尔迭代法和雅各比迭代法，但收敛效率较低；共轭梯度法（CG）以较高的收敛速度而经常被采用。

从理论上讲，一个n阶方程组最多迭代n 步就可求出精确解。

1 直接法直接法就是经过有限步算术运算，无需迭代可直接求得方程组精确解的方法。

但实际计算中由于舍入误差的存在和影响，这种方法也只能得到线性方程组的近似解，该方法是求解低阶稠密矩阵方程组的有效方法。

如Cramer法则，Gauss消元法及其变形（LU分解法、Cholesky 分解法、QR分解法）等。

Matlab中，用矩阵除法“/”或“\”直接求解线性方程组（见附录一），它是一个内部包含着许许多多的自适应算法，对超定方程用最小二乘法求解；对欠定方程因为它的解不唯一，Matlab给出所有解中范数最小的一个特解；对于三对角阵方程组，采用追赶法求解。

2 迭代法迭代法就是用某种极限过程去逐步逼近线性方程组精确解的方法。

该方法具有对计算机的存贮单元需求少，程序设计简单、原始系数矩阵在计算过程中不变等优点，是求解大型稀疏矩阵方程组的重要方法。

迭代法不是用有限步运算求精确解，而是通过迭代产生近似解逼近精确解。

如Jacobi迭代、Gauss-Seidel迭代、SOR迭代法等。

在科学研究和大型工程设计中提出的求解问题，经离散后，常常归结为求解形如Ax = b 的大型线性方程组，此时系数矩阵A和b是通过测量或其它方法得到的，但是在多数情况下方程可能是病态的，即A的条件数非常大。

此时，我们仍然用Matlab中的常规算法，得到的解则可能不是真解。

通常情况下，对系数矩阵A和方程的右端b作微小的扰动，再用上述方法求解，扰动后方程组的解与原方程组的解相差甚远。

线性方程组的共轭梯度法30页PPT文档

W(3) =W*
W(1)
W(2)
沿两个相互正交的方向，进行精确一维搜索，即可得到最优解（二维情形）
罗林开
模式识别与智能系统研究所
2020/6/27
6
n维情形: 沿相互正交的n个方向,进行精确一维搜索,至多迭代n次,即可得到正定二次函数
f (w) 1 wT w rT w 2
的最优解w* r.
f (x) f (x*)f (x*)T(xx*)1(xx*)T A(xx*) 2
f (x*)1(xx*)T A(xx*) 2
因此f (x)的等高面是一簇超椭球面.
罗林开
模式识别与智能系统研究所
2020/6/27
9
x(3) =x* d(2)
x(1) d(1) x(2)
从x(1)出发,沿d(1)作一维搜索,与等高面相切于x(2),记d(2) x* x(2), 再沿d(2)作一维搜索,即可得到最优解x*.由于(d(1))Tf (x(2)) 0, 因此(d(1))T Ad(2) (d(1))T A(x* x(2)) (d(1))T(Ax* Ax(2))
f (w ) f (w *) f (w *)(w w*)
1 (w w *)T I (w w *) 2
f ( w * ) 1 || w w * ||2 . 2
因此 f ( w )的等高模式识别与智能系统研究所
2020/6/27
5
正交方向及其性质
( d ) (1) T A d ( 2 ) 0 则称这两个方向关于 A 共轭 ,或称它们关于 A 正交 . 若 R n中的 k 个方向 d (1) , d ( 2 ) ,L , d ( k ) , 它们两两关于 A 共轭 ,即

共轭梯度法

共轭梯度法1. 算法原理求解一个系数矩阵为正定矩阵的线性方程组可通过求泛函)(x f 的极小值点来获得，进而可以利用共轭梯度法来求解。

共轭梯度法中关键的两点是，确定迭代格式)()()1(k k k k d x x α+=+中的搜索方向)(k d 和最佳步长k α。

实际上搜索方向)(k d是关于矩阵A 的共轭向量，在迭代中逐步构造之；步长k α的确定原则是给定迭代点)(k x 和搜索方向)(k d 后，要求选取非负数k α，使得)()()(k k k d x f α+达到最小，即选择0≥k α，满足)(min )()()(0)()(k k k k k d x f d x f kααα+=+≤。

设迭代点)(k x和搜索方向)(k d已经给定，k α可以通过一元函数)()()()(k k d xf g αα+=的极小化)()(min )()(0k k d xf g ααα+=≤来求得，所以最佳步长)()()()(k k k k k Addd r TT=α。

在给定初始向量)0(x 后，由于负梯度方向是函数下降最快的方向，故第1次迭代取搜索方向)0()0()0()0()(Ax b x f r d-=-∇==。

令)0(0)0()1(d x x α+=，其中)0()0()0()0(0Addd r TT=α。

第2次迭代时，从)1(x 出发的搜索方向不再取()1r，而是选取)0(0)1()1(d r d β+=，使得)1(d与()0d 是关于矩阵A 的共轭向量，即要求)1(d 满足()()()0,01=Ad d ，由此可求得参数)0()0()0()1(0-Ad d Ad r TT=β，然后从()1x 出发，沿方向)1(d进行搜索得)1(1)1()2(d x xα+=，其中1α已由上面k α的计算式获得。

一般地，设已经求出)()()1(k k k k d x x α+=+，计算)1()1(++-=k k Ax b r。

第三章线性代数方程组的共轭梯度法

对于 k = 0 ,1, 2 ,
tk
=
(r(k) )T p(k) (p(k) )T Ap(k)
x (k+1) = x (k) + t k p(k)
r(k+1) = b − Ax(k+1) = r(k) − t k Ap(k)
sk
=
− (p(k) )T Ar(k+1) (p(k) )T Ap(k)
p(k+1) = r (k+1) + sk p(k)
2：在射线x = x(k ) + tp (k )上求f ( x)的极小点x(k +1) , 即 f ( x(k +1) ) = min f ( x(k ) + tp (k ) )
t>0
3：判断 ∇ f ( x (k +1) ) ≤ ε , 或 x(k +1 ) − x(k) ≤ ε ！
是！ x* ≈ x (k +1)，停止 ; 否！ k = k + 1, 转 1.
=
x(0)
+t0p(0).
华北电力大学数理学院
School of mathematics & physics
§3 共轭梯度法
对于 k = 1,2,
现有x ( k )及共轭方向p ( k −1)，则
r(k) = b − Ax(k)
在r ( k )和p ( k −1) 确定的超平面上找共轭方向
其中
p(k) = r(k) + sk p(k−1)
华北电力大学数理学院
School of mathematics & physics
定理1：设p 1 , p 2 , p n 是关于n阶对称正定矩阵A共轭的向量组，则以 p(k)为下降方向的算

共轭梯度算法范文

共轭梯度算法范文共轭梯度算法（Conjugate Gradient Algorithm）是一种优化算法，用于求解解线性方程组或者凸优化问题中的最优解。

它是一种迭代算法，每一步迭代根据梯度方向最优步长，通过求解连续的一系列线性方程来快速收敛。

共轭梯度算法在计算机图形学、机器学习和物理模拟等领域广泛应用。

假设需要求解线性方程组Ax=b，其中A是对称正定矩阵。

我们的目标是找到向量x使得Ax与b之间的残差最小。

共轭梯度算法的步骤如下：1.初始化：选择一个初始解x0和初始残差r0=b-Ax0，其中r0是负梯度方向。

2.计算方向：选择第一个方向p0=r0。

3. 迭代更新：通过计算步长α来更新解向量x(k+1)=xk+αkp，其中αk是标量。

通过最小化残差的二次函数找到最佳步长αk，即αk=(rkTrk)/(pkTApk)。

4. 更新残差：计算新的残差rk+1=rk-αkApk。

5.检查停止条件：判断残差的收敛性，如果满足停止条件则算法终止，否则回到步骤3通过上述迭代步骤，共轭梯度算法能够在较少的迭代次数内快速收敛到最优解。

这主要得益于共轭方向的选择，使得每一次迭代都能够优化残差函数的二次形式。

共轭梯度算法有几个重要的优点。

首先，它适用于求解大型线性方程组，因为它不需要存储整个矩阵。

其次，共轭梯度算法的收敛速度较快，通常比传统的梯度下降算法要快。

最后，共轭梯度算法是一种迭代算法，可以在每一步迭代计算解，因此可以应用于动态系统中。

然而，共轭梯度算法也存在一些局限性。

首先，它只适用于对称正定矩阵，对于非对称矩阵或者非正定矩阵，算法可能会发散。

其次，算法的收敛性依赖于矩阵的条件数，即矩阵的特征值范围。

条件数较大时，算法可能会收敛较慢或者不收敛。

共轭梯度法求解线性方程组

共轭梯度法求解线性方程组闫凡晓 3111054017（数学与统计学院，应用数学）摘要本实验研究了用共轭梯度法求解线性方程组的思想及实现方法，并通过编写Matlab 程序对随机生成的一个线性方程组求解，通过程序的运行调试分析共轭梯度法对不同精度的实际性能，并针对误差进行分析。

关键字共轭梯度法误差容限对称正定矩阵一、实验题目运用共轭梯度法求解一个系数矩阵为对称正定矩阵的线性方程组b Ax =.二、算法思想共轭梯度法是把求解线性方程组的问题转化为求解一个等价的严格凸二次函数的极小化问题。

从任意给定的初始点)0(x出发，沿一组关于A 共轭的方向进行线性搜索，在不考虑舍入误差的情况下，最多迭代n 步（n 是线性方程组的阶数），便可求得二次函数的极小点，也即求得了线性方程组b Ax =的解.对于某些大型稀疏线性方程组,通常该法只经过比方程组阶数n 小得多的迭代次数就能获得所要求精度的近似解.三、算法实现(1)共轭梯度法的简化的计算公式⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧+=-=-=+==-==++++++.,,,,,)()1()1()()()()1()1()1()()()1()()()()()0()0()0(k k k k k T k k T k k k k k k k k k T k k T k k d r d Ad d Ad r Ax b r d x x Ad d d r Ax b r d ββαα（2）基于Matlab 程序的共轭梯度算法实现步骤 1）给定初始近似向量)0(x及精度要求ε<1.0e-4；2）计算,)0()0(Ax b r -=取)0()0(r d =； 3）For 0=k to 1-n do(i),)()()()(kTkkTkk Adddr=α(ii),)()()1(kkkk dxxα+=+(iii),)1()1(++-=k k Axbr(iv)若)1(+krε≤或nk=+1，则输出近似解)1(+kx，停止；否则转（v），（v）22)(22)1(kkkrr+=β，（vi）.)()1()1(kkkk drdβ+=++End do四、实验平台MATLAB 7.6.0五、算法设计%用共轭梯度法求解对称正定线性方程组Ax=b的解clear allA=randint(10,10,[-10,10]);A=A'*A;A=A+A'; %随机生成一个10*10对称正定矩阵Ay=eig(A); %求A的特征值for i=1:10 %判断A的正定性if y(i)<0disp('随机生成的矩阵不是正定矩阵')break;endendb=randint(10,1,[-10,10]); %随机生成一10*1列向量x=randint(10,1,[-10,10]); %随机生成方程初始值iter=10; %最大迭代次数-1tol=1.0e-4; %误差容限d=b-A*x;r=b-A*x;for cnt=1:iter %开始迭代a=(norm(r))^2/(d'*A*d);x=x+a*d;r=b-A*x;if (norm(r)/norm(b))<=toldisp('恭喜您，收敛于误差容限')break;endc=(norm(r)/norm(b-A*(x-a*d)))^2;d=r+c*d;cnt=cnt+1;endz=A\b; %计算方程组的精确解y=norm(x-z);y %精确解与数值解的误差x %数值解cnt %迭代次数六、实验结果y =1.1417e-004x =1.0e+004 *-0.6383-0.3289-0.42850.0773-1.39880.3944-1.47841.08641.5021-0.5389cnt =11恭喜您，收敛于误差容限y =1.3975e-009 x =-0.2072 0.7229 -0.1594 -0.2036 0.2337 0.3801 0.1783 0.0894 -0.6825 -0.4136cnt =10七、实验分析通过以上程序的编写及运行，从获得的数据来说，共轭梯度法基本成功，理论上计算中若无计算误差，则至多迭代n 次就求得了方程组的准确解。

共轭梯度法的预处理

x=x+alpha*C*p;
tol=norm(r); if norm(r)<ep break; end r=r-alpha*A*p; beta=(r'*r)/(r1'*r1); p=r+beta*p; n=n+1; end
%SSOR此处程序改为
x=x+alpha*inv(C')*p
对角预优矩阵
x= 7.85971307544586 0.422926408295008 -0.0735922390240463 -0.540643016894626 0.0106261628540363 m= 4 tol= 4.731753657562764e-04
k 1 (z k 1, z k 1 ) / (rk , z k ),
pk 1 zk 1 k 1 pk
结束。
三、代码
（1）共轭梯度法代码 • function [x,n,tol]=cg(A,b,ep) • r=b;p=r;n=0;x=zeros(length(b),1); • while n<10 • alpha=(r'*r)/(p'*A*p);r1=r; • x=x+alpha*p; • tol=norm(r); • if norm(r)<ep • break; • end • r=r-alpha*A*p; • beta=(r'*r)/(r1'*r1); • p=r+beta*p; • n=n+1; • end
一、知识回顾
对角预优矩阵法如果对称正定线性方程组( 1) 的系数矩阵 A 的对角元素相差较大, 则可取预优矩阵C-1为
C 1 D1 / 2 , D diag (a11, a22 ,, ann ), A (aij )nn

线性代数方程组中的预处理共轭梯度法ppt课件

4 预处理方法
• 预处理方法
•
•
•
•
•
取预优矩阵（预处理矩阵）为A的一个小带宽部分（如三对角或对角线
部分）
矩阵分裂，尤其是线性稳定迭代中的矩阵A的分裂构造预处理矩阵
通过A的各种近似分解得到预处理矩阵（如不完全分解）
通过矩阵A的多项式构造预处理矩阵
子结构，区域分裂，EBE预处理途径等等
4 预处理方法
R中的非零元素远远少于A。R需要显式存储
•
•
•
•
•
第二种高效实现分裂
A是对称的
= 0 − − E ，-E严格下三角，D0是对角线矩阵
M = ( − ) −1 ( − E )，D不完全等于D0
SSOR-PCG
谢谢！
4 预处理方法
• 预处理方法
•
•
•
不完全分解预处理方法：
主要有不完全LU分解、不完全Cholesky分解以及相应的块不完全分解等
设是A的一个近似分解
= + ，L是下三角矩阵，R称为剩余矩阵，M= 为预处理矩阵。
此方法与CG迭代方法相结合，就形成了不完全Cholesky分解预处理共轭
1 引入
• 线性代数方程组的解法
• 直接法：高斯消去法，分解法
• 迭代法：
•
•
古典迭代法：Jacobi，Gauss-Seidel，SOR，SSOR
现代迭代法：（投影方法，子空间法）
•
•
•
•
正交化的误差投影型Krylov：FOM，IOM，DIOM
对称情形误差投影型Krylov：Lanczos，CG，PCG
• 预处理方法
•
对角预处理法：

共轭梯度法

又称共轭斜量法，是解线性代数方程组和非线性方程组的一种数值方法，例如对线性代数方程组A尣＝ƒ, (1)式中A为n阶矩阵，尣和ƒ为n维列向量,当A对称正定时,可以证明求(1)的解尣*和求二次泛函(2)的极小值问题是等价的。

此处(尣,у)表示向量尣和у的内积。

由此，给定了初始向量尣，按某一方向去求(2)取极小值的点尣,就得到下一个迭代值尣,再由尣出发，求尣等等，这样来逼近尣*。

若取求极小值的方向为F在尣(k＝1,2,…)处的负梯度方向就是所谓最速下降法，然而理论和实际计算表明这个方法的收敛速度较慢，共轭梯度法则是在尣处的梯度方向r和这一步的修正方向p所构成的二维平面内，寻找使F减小最快的方向作为下一步的修正方向,即求极小值的方向p（其第一步仍取负梯度方向）。

计算公式为再逐次计算(k=1,2,…)。

可以证明当i≠j时，从而p,p形成一共轭向量组;r,r,…形成一正交向量组。

后者说明若没有舍入误差的话，至多n次迭代就可得到(1)的精确解。

然而在实际计算中,一般都有舍入误差，所以r,r,…并不真正互相正交，而尣尣,…等也只是逐步逼近(1)的真解,故一般将共轭梯度法作为迭代法来使用。

近来在解方程组(1)时,常将共轭梯度法同其他一些迭代法结合作用。

特别是对病态方程组这种方法往往能收到比较显著的效果。

其方法是选取一对称正定矩阵 B并进行三角分解，得B=LL T。

将方程组(1)化为hу＝b, (3)此处y＝l T尣,b＝l-1ƒ,h＝l-1Al-T,而。

再对(3)用共轭梯度法，计算公式为(k=0,1,2,…)适当选取B，当B 很接近A时，h的条件数较之A大大减小,从而可使共轭梯度法的收敛速度大为加快，由一些迭代法的矩阵分裂A=M -N，可选取M 为这里的B，例如对称超松弛迭代(SSOR)，强隐式迭代(SIP)等,这类方法常称为广义共轭梯度法或预条件共轭梯度法，它也可用于解代数特征值问题。

势函数的一种二阶偏微分方程。

共轭梯度法结论

共轭梯度法结论
共轭梯度法是一种常用的非线性优化算法，特别适合求解带正定对称矩阵的线性方程组。

该方法的基本思路是通过构建共轭方向序列，在每个方向上进行一维搜索，从而最小化一个二次型的目标函数。

共轭梯度法具有高精度、高效率、不需要存储大规模矩阵等优点，在科学计算、数学建模、图像处理等领域得到广泛应用。

共轭梯度法的基本结论可以概括为以下几点：
1. 共轭梯度法解决的是线性方程组求解问题。

其中，矩阵必须是正定对称的，否则求解过程可能不收敛，甚至得到错误解。

2. 共轭方向序列是该方法的核心。

共轭方向序列包括预处理共轭梯度法、FR共轭梯度法、PR共轭梯度法、PRP共轭梯度法等多种变体。

这些方法在不同条件下表现不同，选择合适的共轭方向序列能够提高算法收敛速度和精度。

3. 共轭梯度法并不需要储存大规模矩阵，而是利用矩阵向量乘法进行计算。

这一特点使得算法可以用于解决大规模矩阵问题，节省了存储和计算资源。

4. 共轭梯度法求解线性方程组问题的计算量和存储量都比其他经典方法如高斯消元、LU分解等小得多。

同时，算法的迭代次数与矩阵的条件数近似成反比例关系，可以提高求解精度。

5. 共轭梯度法也有一些局限性。

例如，在非正定矩阵情况下可能会出现振荡，需要使用修正的共轭梯度法，如拟共轭梯度法或CGS等。

总之，共轭梯度法是一种重要的数值优化算法，可以用于求解线性方程组等一系列问题。

要充分发挥其优点，需要根据实际问题选择合适的共轭方向序列，并注意算法的局限性。

线性代数方程组中的预处理共轭梯度法

医学资料
• 仅供参考,用药方面谨遵医嘱
1 引入
• CG算法
残差向量搜索步长搜索方向
2 知识回顾
3 算法原理
3 算法原理
4 预处理方法
• 预处理方法
• 取预优矩阵（预处理矩阵）为A的一个小带宽部分（如三对角或对角线部分）
• 矩阵分裂，尤其是线性稳定迭代中的矩阵A的分裂构造预处理矩阵 • 通过A的各种近似分解得到预处理矩阵（如不完全分解） • 通过矩阵A的多项式构造预处理矩阵 • 子结构，区域分裂，EBE预处理途径等等
4 预处理方法
4 预处理方法
4 预处理方法
5 高效实现
谢谢！
人有了知识，就会具备各种分析能力，明辨是非的能力。所以我们要勤恳读书，广泛阅读，古人说“书中自有黄金屋。 ”通过阅读科技书籍，我们能丰富知识，培养逻辑思维能力；通过阅读文学作品，我们能提高文学鉴赏水平，培养文学情趣；通过阅读报刊，我们能增长见识，扩大自己的知识面。有许多书籍还能培养我们的道德情操，给我们巨大的精神力量，鼓舞我们前进。
线性代数方程组中的预处理共轭梯度
法
1 引入
• 线性代数方程组的解法
• 直接法：高斯消去法，分解法 •迭代法：
• 古典迭代法：Jacobi，Gauss-Seidel，SOR，SSOR • 现代迭代法：（投影方法，子空间法）
• 正交化的误差投影型Krylov：FOM，IOM，DIOM • 对称情形误差投影型Krylov：Lanczos，CG，PCG • 正交化的残量投影型Krylov：GMRES，GCR • 双正交化投影型Krylov方法：BiCG，CGS…..

矩阵计算与分析-求解方程组-预处理共轭梯度法

可以证明，经过这样的预处理，F =S−1AS−T 的条件数大约是A的条件数的平方根．特别是ω = 1情形，即对称的GS迭代预处理会有好的效果．
(1) ∀u(0)∈R n， ~ ( 0 ) = g − Fu( 0 ) , ~ ~ (0) , ( 2) 令 r p(0) = r (3)对k =0 ,1 , … , ~(k ) , r ~(k ) ) r ( ~ = α k (~ p ( k ) , S −1 AS −T ~ p(k ) )
(k ) ~ ~ u( k +1 ) = u( k ) + α p k (k ) ~ ( k +1 ) = r ~(k ) − α ~ S −1 AS −T ~ r p k ( k +1 ) ~ ( k +1 ) ~ r ) ( ,r ~ βk = ~ ( k ) ~ ( k ) (r , r ) ~ ~(k ) ( k +1 ) ( k +1 ) ~ ~ p =r + βk p
9.4.5 预处理共轭梯度法
由 x
(k )
⎛ K − 1 ⎞ (0) − x * A ≤ 2⎜ ⎟ x − x* A ⎝ K + 1⎠
k
可以看到，当A病态时有K>>1， CG法收敛将很慢．为了改善收敛性，可以设法先降低矩阵的条件数，这就是预处理方法．
当 A对称正定时，希望预处理后的方程组仍保持对称正定，为此，设 S 可逆，
M = SS T (7.19) x = S −T u g= S b,
−1
M是对称正定阵，把 Ax = b改写为等价的方程组
S −1 AS −T u = S −1b , F = S AS
−1 −T
新方程组的系数矩阵保持了对称正定．令

eigen共轭梯度

eigen共轭梯度Eigen共轭梯度法是一种常用的优化算法，广泛应用于解决线性方程组、最小二乘问题和特征值问题等数值计算中。

本文将对Eigen 共轭梯度法进行详细介绍，并探讨其原理、特点及应用。

一、算法原理Eigen共轭梯度法是一种迭代法，用于求解对称正定矩阵的线性方程组Ax=b。

它的基本思想是通过一系列迭代步骤逐渐逼近方程组的解。

我们需要了解共轭梯度法的两个重要概念：共轭和梯度。

对于两个非零向量x和y，如果它们满足x^T Ay=0，则称x和y是关于矩阵A共轭的。

而梯度则是目标函数在某一点的导数，用于确定下降方向。

具体而言，Eigen共轭梯度法的步骤如下：1. 初始化解向量x0和残差向量r0，设初始残差r0=b-Ax0。

2. 计算初始搜索方向d0=r0。

3. 迭代更新解向量和残差向量：a. 计算步长alpha_k=(r_k^T r_k) / (d_k^T A d_k)。

b. 更新解向量x_k+1=x_k+alpha_k*d_k。

c. 更新残差向量r_k+1=r_k-alpha_k*A*d_k。

d. 计算搜索方向d_k+1=r_k+1+beta_k*d_k，其中beta_k=(r_k+1^T r_k+1) / (r_k^T r_k)。

4. 重复步骤3，直到收敛或达到迭代次数。

二、算法特点Eigen共轭梯度法相比于传统的直接求解方法具有以下几个特点：1. 内存占用小：共轭梯度法只需要存储解向量和残差向量，而不需要存储完整的矩阵。

2. 迭代次数少：对于对称正定矩阵，Eigen共轭梯度法通常能够在较少的迭代次数下收敛，从而加快计算速度。

3. 数值稳定性好：由于共轭梯度法是一种迭代法，它能够避免由于舍入误差而导致的数值不稳定问题。

4. 适用范围广：Eigen共轭梯度法不仅适用于线性方程组的求解，还可以用于求解最小二乘问题和特征值问题等。

三、算法应用Eigen共轭梯度法在科学计算和工程领域有着广泛的应用，例如：1. 图像处理：在图像处理中，常常需要对大型图像进行处理和分析。

线性代数方程组中的预处理共轭梯度法

共轭梯度法

共轭梯度法原理

3_共轭梯度法

——共轭梯度法ppt课件

计算方法——共轭梯度法求解线性方程组

共轭梯度法求解线性方程组

利用共轭梯度法求解线性方程组

线性方程组的共轭梯度法30页PPT文档

共轭梯度法

第三章 线性代数方程组的共轭梯度法

共轭梯度算法范文

共轭梯度法求解线性方程组

共轭梯度法的预处理

线性代数方程组中的预处理共轭梯度法ppt课件

共轭梯度法

共轭梯度法结论

线性代数方程组中的预处理共轭梯度法

矩阵计算与分析-求解方程组-预处理共轭梯度法

eigen共轭梯度

第三章线性代数方程组的共轭梯度法