工程电磁场数值分析5(有限元法) Ansys工程电磁场有限元分析 华科电气共74页
合集下载
《电磁场有限元分析》课件
计算量大
对于大规模问题，有限元分析需要处理大量的 数据和计算，计算成本较高。
对初值和参数敏感
有限元方法对初值和参数的选择比较敏感，可 能会影响求解的稳定性和精度。
数值误差
有限元方法存在一定的数值误差，可能会导致结果的精度损失。
未来发展方向和挑战
高效算法
研究更高效的算法和技术，提高有限 元分析的计算效率和精度。
网格划分的方法
根据实际问题选择合适的网格类型，如四面体网 格、六面体网格等，并确定网格的大小和密度。
数据准备的内容
准备边界条件、初始条件、材料属性等数据，为 后续计算提供必要的数据支持。
有限元方程的求解和后处理
求解方法的选择
根据实际问题选择合适的求解方法，如直接求解法、 迭代求解法等。
求解步骤
将有限元方程组转化为线性方程组，选择合适的求解 器进行求解，得到各节点的数值解。
电磁场有限元分析简介
概述有限元分析的基本原理和方 法，包括离散化、近似函数、变
分原理等。
介绍电磁场有限元分析的基本步 骤，包括前处理、求解和后处理
等。
简要介绍电磁场有限元分析的常 用软件和工具，如ANSYS、 COMSOL Multiphysics等。
02
电磁场理论基础
麦克斯韦方程组
总结词
描述电磁场变化规律的方程组
详细描述
边界条件和初始条件是描述电磁场在边界和初始时刻的状态，对于求解电磁场问 题至关重要。
03
有限元方法基础
有限元方法概述
01
有限元方法是一种数值分析方法，通过将连续的物理域离散化 为有限数量的单元，利用数学近似方法求解复杂的问题。
02
该方法广泛应用于工程领域，如结构分析、流体动力学、电磁
电磁应力 Ansys工程电磁场有限元分析 华科电气
电磁张量divij上述公式反映了法拉第和maxwell对电磁力的看法他们认为电磁力是靠连续的弹性媒质即以太来传递的
1.电磁张Leabharlann 与电磁力：电磁张量定义：
有：
应用散度定理，得到：
式中， 。
上述公式反映了法拉第和Maxwell对电磁力的看法，他们认为，电磁力是靠连续的弹性媒质（即以太）来传递的。后来的研究表明，以太的假设不是必要的，但是上述公式给出了计算电磁力的正确结果。
对于包围在体积V内的静止电荷和恒定电流，有下列关系式：
2.虚功原理：
二维静态磁场分析：
1.电磁张Leabharlann 与电磁力：电磁张量定义：
有：
应用散度定理，得到：
式中， 。
上述公式反映了法拉第和Maxwell对电磁力的看法，他们认为，电磁力是靠连续的弹性媒质（即以太）来传递的。后来的研究表明，以太的假设不是必要的，但是上述公式给出了计算电磁力的正确结果。
对于包围在体积V内的静止电荷和恒定电流，有下列关系式：
2.虚功原理：
二维静态磁场分析：
有限元ansys电磁场分析详解PPT课件
• 选择 OK
• 选择OK
第4页/共33页
• 重复这些步骤，定义定子磁体材料3
• 为转子磁体平行磁化方向定义11号局部坐标系 • 水平方向反时针30度（总体坐标+X 轴） • 局部坐标系原点与总体坐标系一致 Utility>workplane>local coord. systems>create local CS>at specified location
• 选择 OK • 与前面一样重新设置衔铁的关联 • 对除有约束方程的节点外的所有外部节点重新施加平行条件 • 执行求解
第29页/共33页
• 显示磁通密度和磁力线迭加图 – 由于衔铁位置改变，磁力线随 着变化 – 定子内最大磁密BSUM增大 – 模型交界处磁场连续
BSUM (T)
第30页/共33页
谢谢您的观看！
第33页/共33页
2.5-33
第17页/共33页
• 模拟有许多磁极的电机，周期性边界 条件非常有用
• 右图显示的是一个10极永磁电机
• 模拟转子的运动。当转子转动时，电 流会变化。
• 定子槽内显示电流密度
• 本模型也允许转子和定子相互独立
• 观看动画，可执行动画文件:
mach2d.avi
定子
第18页/共33页
转子
约束方程—不相同网格
• 将定子一侧边界上的节点建立组件. • 选择定子模型边界上线段 • 选择STATOR组件 • 再选择边界上线段 • 选择所选线段上的全部节点 • 建立单节点组件CE_N
第22页/共33页
定子内半径 全部节点
• 选择衔铁组件ARMATURE • 选择节点组件 CE_N • 应用约束方程生成器
Preproc>coupling/ceqn>adjacent regions
• 选择OK
第4页/共33页
• 重复这些步骤，定义定子磁体材料3
• 为转子磁体平行磁化方向定义11号局部坐标系 • 水平方向反时针30度（总体坐标+X 轴） • 局部坐标系原点与总体坐标系一致 Utility>workplane>local coord. systems>create local CS>at specified location
• 选择 OK • 与前面一样重新设置衔铁的关联 • 对除有约束方程的节点外的所有外部节点重新施加平行条件 • 执行求解
第29页/共33页
• 显示磁通密度和磁力线迭加图 – 由于衔铁位置改变，磁力线随 着变化 – 定子内最大磁密BSUM增大 – 模型交界处磁场连续
BSUM (T)
第30页/共33页
谢谢您的观看！
第33页/共33页
2.5-33
第17页/共33页
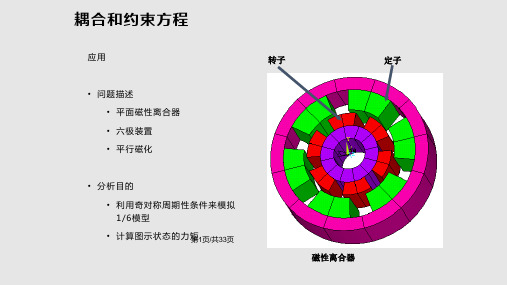
• 模拟有许多磁极的电机，周期性边界 条件非常有用
• 右图显示的是一个10极永磁电机
• 模拟转子的运动。当转子转动时，电 流会变化。
• 定子槽内显示电流密度
• 本模型也允许转子和定子相互独立
• 观看动画，可执行动画文件:
mach2d.avi
定子
第18页/共33页
转子
约束方程—不相同网格
• 将定子一侧边界上的节点建立组件. • 选择定子模型边界上线段 • 选择STATOR组件 • 再选择边界上线段 • 选择所选线段上的全部节点 • 建立单节点组件CE_N
第22页/共33页
定子内半径 全部节点
• 选择衔铁组件ARMATURE • 选择节点组件 CE_N • 应用约束方程生成器
Preproc>coupling/ceqn>adjacent regions
工程电磁场数值分析(有限元法)解读课件
有限元法在工程电磁场中的应用
在静电场中，电荷分布是确定的，电场强度和电位是求解的目标。有限元法可以将连续的静电场离散化为有限个单元，通过求解离散化的方程组来得到电场强度和电位。
有限元法在静电场问题中能够有效地处理复杂的边界条件和电荷分布，为工程实际中静电场问题的求解提供了有效的数值分析方法。
在静电场问题中，有限元法将连续的求解区域离散化为有限个单元，每个单元内的电荷分布被假设为均匀分布。通过将电场强度和电位表示为单元中心点的插值函数，可以建立离散化的方程组。求解该方程组可以得到每个单元中心点的电场强度和电位，从而得到整个区域的电场分布。
静电场问题
总结词
详细描述
在静磁场中，磁力线是闭合的，磁场强度是确定的。有限元法可以将连续的静磁场离散化为有限个单元，通过求解离散化的方程组来得到磁场强度和磁感应强度。
有限元法在静磁场问题中能够有效地处理复杂的边界条件和磁场分布，为工程实际中静磁场问题的求解提供了有效的数值分析方法。
在静磁场问题中，有限元法将连续的求解区域离散化为有限个单元，每个单元内的磁场分布被假设为均匀分布。通过将磁场强度和磁感应强度表示为单元中心点的插值函数，可以建立离散化的方程组。求解该方程组可以得到每个单元中心点的磁场强度和磁感应强度，从而得到整个区域的磁场分布。
02
诺依曼边界条件
规定电场和磁场在边界处的法向分量，与狄利克雷边界条件一起使用。
STEP 01
STEP 02
ห้องสมุดไป่ตู้
STEP 03
有限元法基础
结构分析
用于分析各种结构的应力、应变、位移等。
流体动力学
用于分析流体流动、传热等问题。
电磁场
用于分析电磁场分布、电磁力、电磁感应等问题。
电磁场有限元方法
电磁场有限元方法
电磁场有限元方法是一种用于求解电磁场分布的数值计算方法。
它基于有限元法，将连续的电磁场问题离散化为有限个区域，通过计算每个区域内的电磁场变量进行求解。
在电磁场有限元方法中，电磁场通常通过两个基本变量来描述：电场和磁场。
这些变量可通过Maxwell方程组进行表达，并且可以通过有限元法对其进行离散化。
在离散化过程中，整个计算区域被划分为小的有限单元，并在每个单元上建立适当的数学模型。
然后，通过求解相应的矩阵方程组，可以得到每个单元内的电磁场变量的近似解。
电磁场有限元方法的求解步骤通常包括以下几个步骤：
1. 网格划分：将计算区域划分为小的有限单元。
2. 建立数学模型：在每个单元上建立适当的数学模型来描述电磁场变量的行为。
3. 生成方程组：通过应用Maxwell方程组和适当的边界条件，可以得到矩阵方程组。
4. 求解方程组：使用数值求解方法，如迭代法或直接法，求解得到每个单元内的电磁场变量的近似解。
5. 后处理：根据得到的解，可以计算出其他感兴趣的物理量，如电流密度，功率密度等。
电磁场有限元方法在计算电磁场分布时具有很好的灵活性和精确性。
它广泛应用于电磁设备的设计和分析，如电机、变压器、传感器等。
电磁场有限元分析ANSYS ppt课件
FEA internally coupled with circuit elements
Coupled with external circuits using Schematic
Three phase power transformer
15
Rectifier Circuit
16
17
Eddy Currents Induced in an Aluminum Plate
法。。。，对简单场域，单一介质、规则场域适用，物理含义清楚
➢ 数值解法 现代计算方法，复杂场域、多介质、各向异性介质，几乎
所有场域问题
7
0绪
4.数值解法的种类
➢ 有限差分法 （Finite Difference Methods FDM） ➢ 有限元素法（Finite Elements Methods FEM） ➢ 体积分方程法 (Volume Integral Equation Methods VIEM) ➢ 边界元素法(Boundary Elements Methods BEM) ) ➢ 混合法 (Hybrid Methods) ➢ ………
Coil
Aluminum Plate
Time average values: Power loss (eddy solver) = 4.60 W
Power loss (transient) = 4.46 W
18
19
20
21
电磁场有限元分析
0 绪论
1 电磁场理论回顾 （电磁场微分方程）
2 有限元原理
（加权余量法、变分法、边界条件）
3 有限元实施
（1，2维）
4 有限元求解电磁场问题的现代方法
（有限元计算软件的使用）
工程电磁场数值分析解读
工程电磁场数值分析解读工程电磁场数值分析是一种应用有限元法来计算和解决电磁场问题的方法。
该方法通过将电磁场的连续性方程离散化为有限个小单元，再通过求解矩阵方程组来获取数值解。
这种分析方法能够定量计算电磁场的分布和特性，并为工程设计和优化提供重要的参考依据。
对于电磁场数值分析的解读，可以从以下几个方面进行讨论：首先，可以对电磁场的分布进行解读。
通过数值计算，可以得到电磁场在不同位置的数值结果，可以用来表示电磁场的强弱、方向和空间分布特性。
可以对电磁场的分布情况进行比较和分析，以评估电磁场的均匀性和一致性，为设计提供优化方案。
其次，可以对电磁场的特性进行解读。
通过数值计算，可以计算并分析电磁场的一些重要参数，如电场强度、磁场强度、电势、电感、电容等。
这些参数能够揭示电磁场的基本特性，并对电磁设备和系统的工作性能进行评估和优化。
另外，可以对电磁场的影响进行解读。
电磁场数值分析能够计算出电磁场对物体的作用效果，如力、热、电磁感应等。
通过对电磁场的影响进行解读，可以预测电磁场对设备、器件和系统的影响，并为电磁兼容性设计提供技术支持。
此外，还可以对电磁场数值分析方法和结果的准确性进行解读。
电磁场数值分析是一种近似求解的方法，所得数值结果可能与实际情况存在一定差异。
因此，在解读时需要对数值结果进行验证和确认，通过模型实验或其他可靠手段来验证模型的准确性和可靠性。
总之，工程电磁场数值分析是一种重要的工程设计方法，能够定量计算和解决电磁场问题。
通过对电磁场分布、特性和影响等方面进行解读，可以为工程设计和优化提供重要的参考依据。
同时也需要关注分析方法的准确性和结果的可靠性，以确保分析结果的准确性。
工程电磁场数值分析有限元法解读31页PPT
25、学习是劳动，是充满思想的也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤，荒于嬉；行成于思，毁于随。——韩愈
23、一切节省，归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰，决心到最后会全部推倒。——莎士比亚
工程电磁场数值分析有限元法解读
11、获得的成功越大，就越令人高兴 。野心 是使人 勤奋的 原因， 节制使 人枯萎 。 12、不问收获，只问耕耘。如同种树 ，先有 根茎， 再有枝 叶，尔 后花实 ，好好 劳动， 不要想 太多， 那样只 会使人 胆孝懒 惰，因 为不实 践，甚 至不接 触社会 ，难道 你是野 人。(名 言网) 13、不怕，不悔(虽然只有四个字，但 常看常 新。 14、我在心里默默地为每一个人祝福 。我爱 自己， 我用清 洁与节 制来珍 惜我的 身体， 我用智 慧和知 识充实 我的头 脑。 15、这世上的一切都借希望而完成。 农夫不 会播下 一粒玉 米，如 果他不 曾希望 它长成 种籽； 单身汉 不会娶 妻，如 果他不 曾希望 有小孩 ；商人 或手艺 人不会 工作， 如果他 不曾希 望因此 而有收 益。-- 马钉路 德。
23、一切节省，归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰，决心到最后会全部推倒。——莎士比亚
工程电磁场数值分析有限元法解读
11、获得的成功越大，就越令人高兴 。野心 是使人 勤奋的 原因， 节制使 人枯萎 。 12、不问收获，只问耕耘。如同种树 ，先有 根茎， 再有枝 叶，尔 后花实 ，好好 劳动， 不要想 太多， 那样只 会使人 胆孝懒 惰，因 为不实 践，甚 至不接 触社会 ，难道 你是野 人。(名 言网) 13、不怕，不悔(虽然只有四个字，但 常看常 新。 14、我在心里默默地为每一个人祝福 。我爱 自己， 我用清 洁与节 制来珍 惜我的 身体， 我用智 慧和知 识充实 我的头 脑。 15、这世上的一切都借希望而完成。 农夫不 会播下 一粒玉 米，如 果他不 曾希望 它长成 种籽； 单身汉 不会娶 妻，如 果他不 曾希望 有小孩 ；商人 或手艺 人不会 工作， 如果他 不曾希 望因此 而有收 益。-- 马钉路 德。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
代入方程得余量：
i1
RL(u)f
在有限元法中，基函数一般用 {Ni,i1,2, ,n}表示。
采用Galerkin方案，取权函数与基函数相同。使与余量正交 化：
(N i,R ) N i[L (u)f]d 0 (i1, 2, , n)
加权余量法回顾（续） (N i,R ) N i[L (u)f]d 0
工程电磁场数值分析
（有限元法）
华中科技大学电机与控制工程系
陈德智
2019.12
第4章 电磁场有限元法 （Finite Element Method, FEM）
有限元法可以基于变分原理导出，也可以基于加权 余量法导出，本章以加权余量法作为有限元法的基础， 以静电场问题的求解为例介绍有限元法的基本原理与实 施步骤。并介绍有限元法中的一些特殊问题。
K0116N0L(N1)d
b Nfd 0 1 2 3 4 5 6 0
以下把单元e的贡献记为
K(e) ij
eNi(e)L(N(je))d
b(e) i
e
N(e) i
f(e)d
这样，就有
K 0 0 K 0 ( 1 0 ) K 0 ( 0 2 ) K 0 ( 0 3 ) K 0 ( 0 4 ) K 0 ( 0 5 ) K 0 ( 0 6 )
y y2 y3
111 1 2 2 x1 x x3
y1 y y3
单元节点的编号按 逆时针方向排列！
1 11 1 3 2 x1 x2 x
y1 y2 y
u (x ,y ) u 1 1 ( x ,y ) u 2 2 ( x ,y ) u 3 3 ( x ,y )
记住我们的任务 —寻找基函数
作用后值为0。但是，在相邻单元的边
界上， Ni是连续但是不光滑的，因此对 积分的贡献主要来自边界。为考虑单元
边界的影响，需要借助于格林公式：
格林公式： V ( 2 )d V S d S
K i ( je ) eN i 2 ( N j) d x d y e N i N jd x d y eN i N n jd
在积分 Kij NiL(Nj)d中，对于确定的 i，j的有效取
值为i本身以及与节点i相联的周围节点，积分的有效区域为 以i、j为公共节点的所有三角形单元 ，在这些单元中Ni、Nj 才有交叠。
这些积分可以分单元进行。例如对 右图所示的局部编码，K01、K00以及 b0的计算公式为：
K 00 1 2 3 4 5 6N 0L (N 0)d
得代数方程组： Kαb
场域离散
以二维静电场泊松方程的求解为例。二维问题常使用三角 形单元离散，便于处理复杂的场域形状，容易实现。
单元：互不重叠，覆盖全部场域；每个单元内介质是 单一、均匀的。
节点：网格的交点，待求变量的设置点。 需要记录信息： 节点编号、节点坐标 节点属性(激励源、是否边界等) 单元编号 单元节点编号 单元介质
第4章 电磁场有限元法（FEM）
1. 有限元的基本原理与实施步骤 2. 有限元方程组的求解 3. 前处理与后处理技术 4. 渐近边界条件 5. 矢量有限元法 6. 求解运动导体涡流问题的迎风有限元法
1. 有限元法的基本原理与实施步骤
加权余量法回顾：
对算子方程
L(u) f
n
用 u 作为该方程的近似解（试探解）：u i i
K01K0(11) K0(16)
b 0 b 0 ( 1 ) b 0 ( 2 ) b 0 ( 3 ) b 0 ( 4 ) b 0 ( 5 ) b 0 ( 6 )
每个 K
(e) ij
或
b (e) i
的计算都在具体的单元内单独考虑（称
为单元分析）。
三角形单元内的基函数 设三角形三个顶点处待求函数值 分别为u1, u2, u3。如果单元足够小， 可以采用线性近似，将单元内任 意p点的u(x,y)表示为
u(x,y)abxcy
代入三个顶点的坐标和函数值， 可以解出a、b、c。得到
u (x ,y ) u 1 1 ( x ,y ) u 2 2 ( x ,y ) u 3 3 ( x ,y )
111
其中，
1 2
x1
x2
x3
y1 y2 y3
11 1 1 1 2 x x2 x3
（1）是插值的；
1 (i j) （2）Ni(xj,yj)0 (i j) （3）在相邻单元的公共边界上，
Ni是连续的，从而通过Ni构造的逼近函数也是连续的。
单元分析：计算单元内积分对系数阵和右端项元素的贡献。
系数阵元素：
K(e) ij
eNi(e)L(N(je))d
当L为拉普拉斯算子时，由于Ni在单元 内是(x, y)的线性函数，经Laplace算子
u (x ,y )1 N 12 N 23 N 3
对比 u (x ,y ) u 1 u 3 3 ( x ,y )
可得
Ni
i (x,
y)
( i 1, 2, 3)
基函数Ni常被称为插值函数或者形状函数，具有以下性质：
Ki,j NiL(Nj)d bi Ni fd
目标：建立节点变量之间满足的 代数方程组，即确定系数{Kij} 和 {bi}。依据的原理是加权余量法 使用的基函数为分域基。
基函数
有限元采用分片逼近的思想，跟 使用折线逼近一条任意曲线的做 法相同。使用分域基Ni，基函数 的个数等于节点的个数；每个基 函数Ni的作用区域是与该节点i相 关联的所有单元。
n
设L为线性算子，代入 u i N i ，得 i1
n
n
N i[L ( jN j) f]d N i[ jL (N j) f]d 0
j 1
j 1
n
或
j NiL(Nj)dNi fd (i1, 2, , n)
j1
记 Ki,j NiL(Nj)d bi Ni fd