最新快速解耦法
(仅供参考)ETAP软件潮流计算方法

分析案例编辑器
分析案例文件夹标识(Study Case ID)
分析案例文件夹标识显示在输入区。删除旧的标识,输入新的就可以改变分析案例文件夹的 名字了。分析案例文件夹标识 不超过 12 个字母,使用编辑器底部的浏览器,可以从一个案例切 换到另一个案例。
方法(Method)
在本部分中选择一个潮流分析案例文件夹。有三种方法可选:牛顿-拉夫逊、快速解耦法和加 速高斯—塞德尔法
没有(None)
选择没有单选框,用在所选负荷类型中输入的每条负荷的百分数。
母线最大(Bus Maximum)
当选择最大负荷选项时,所有电动机和其它直接与每条母线相连的负荷将乘以母线最大调整 系数。利用该选项,您可以用不同的最大调整系数对母线进行模拟潮流分析。
当考虑到将来电力系统负荷和每条母线有不同的最大负荷时,该选项有很大作用。
输入迭代次数的最大值。如果在达到设定的迭代次数后,精度仍无法收敛,则程序停止运行 并通知用户。对于高斯-塞德尔方法推荐值是 2000, 对于牛顿-拉夫逊法 和快速解耦方法推荐值是 5。
精度( Precision)
输入参数的精度值,用于检验该精度的收敛度。该值决定了您想要最终结果精确到什么程 度。对于高斯-塞德尔方法,精度用于在每次迭代之后检查母线电压之间的差距。对于牛顿-拉夫 逊和快速解耦方法,精度用于比较不同迭代之间每条母线的功率差。如果迭代之间的差小于或等 于输入的精度值,则要求 的精度就达到了。
作为 PowerStation®三维数据库概念的一部分,分析案例可用于三个主要系统组成部分的任意 组合,也就是适用于任何配置参数,单线图图形显示和基本/修正版本数据。
处于潮流分析时,在潮流分析案例工具条中点击“分析案例”就可以访问潮流分析案例编辑 器了。也可以从项目视图中点击潮流 分析案例文件夹来访问该编辑器。
现代电力系统潮流计算作业

现代电力系统——潮流计算作业0 序章作业要求(A组):0.1 调用matpower中的runpf函数,分析输入文件中各矩阵定义;0.2 调用某一个算例,输出潮流结果,并分析。
0.3完成0.1和0.2的基础上,分析matpower中牛顿法和快速解耦法,给出流程图,写出newtonpf和fdpf函数每行程序定义。
0.4 完成0.3的基础上,制造一个病态潮流算例,并跟踪调试,分析病态原因。
1分析输入文件中各矩阵的定义1.1 MATPOWER的安装MATPOWER工具箱的安装步骤如下:1)下载matpower压缩包。
官方下载网址:/matpower/,目前最新版本为6.0b1,稳定版本为5.1,建议下载稳定版本。
2)解压压缩包,得到文件夹matpower5.1,并将文件夹移动到MATLAB所在路径的toolbox文件夹下。
我的路径为:C:\Program Files\MATLAB\R2016a\toolbox。
3)添加地址到MATLAB路径。
打开MATLAB,点击“文件”→“设置路径”→“添加并包含子文件夹…”,找到matpower5.1所在的位置,点击“确定”,再点“保存”→“关闭”。
4)测试matpower工具是否安装成功。
在MATLAB命令行窗口输入“test_matpower”,出现一系列的测试,均显示“ok”,最后显示“All tests successful (3256 passed, 682 skipped of 3938)”,则表示安装成功。
1.2 矩阵的定义打开文档“caseformat.m”,或者在MATLAB命令行窗口中输入“help caseformat”,可以得到关于输入矩阵的数据定义。
当然,也可以参考docs文件夹下的manual文档,其中对matpower工具箱进行了详细说明。
在matpower中,输入矩阵至少包含三种:母线参数矩阵(Bus Data),发电机参数矩阵(Generator Data),支路参数矩阵(Branch Data)。
现代电力系统分析-往年试卷与复习资料 (6)

一、潮流计算方法之间的区别联系高斯-赛德尔法:原理简单,导纳矩阵对称且高度稀疏,占用内存小。
收敛速度很慢,迭代次数随节点数直接上升,计算量急剧增加,不适用大规模系统。
牛顿-拉夫逊法:收敛速度快,迭代次数和网络规模基本无关。
相对高斯-赛德尔法,内存量和每次迭代所需时间较多,其可靠的收敛还取决于一个良好的启动初值。
PQ 分解法(快速解耦法):PQ 分解法实际上是在极坐标形式的牛顿法的基础上,在交流高压电网中,输电线路等元件的R<<X ,即有功功率主要取决于电压相角,而无功功率主要取决于电压幅值,根据这种特性对方程组进行简化,从而实现了有功和无功的解耦。
两大条件:(1)线路两端的相角相差不大(小于10°~20°),而且||||ij ij G B ≤,于是可以认为:cos 1;sin ij ij ij ij G B θθ≈≤; (2)与节点无功功率相对应的导纳2/i i Q U 通常远小于节点的自导纳ii B ,也即2i i ii Q U B <<。
1. PQ 分解法用一个1n -阶和一个1n m --阶的方程组代替牛顿法中22n m --阶方程组,显著减少了内存需量和计算量。
2. 计算过程中B '、B ''保持不变,不同于牛顿法每次迭代都要重新形成雅可比矩阵,因此显著提高了计算速度。
3.雅可比矩阵J 不对称,而B '、B ''都是对称的,使求逆等运算量和所需的存储容量都大为减少。
4. PQ 分解法的迭代次数要比牛顿法多,但是每次迭代所需时间比牛顿法少,所以总的计算速度仍是PQ 分解法快。
在低压配电网中PQ 分解法不适用。
交流高压电网的输电线路的元件满足R<<X ,PQ 分解法正是基于此条件简化而来;而低电压配电网络一般R/X 比值很大,大R/X 比值病态问题也正是PQ 分解法应用中的一个最大障碍。
电力系统潮流分析与计算设计(P Q分解法)

电力系统潮流分析与计算设计(P Q分解法)电力系统潮流分析与计算设计(p-q分解法)摘要潮流排序就是研究电力系统的一种最基本和最重要的排序。
最初,电力系统潮流排序就是通过人工手算的,后来为了适应环境电力系统日益发展的须要,使用了交流排序台。
随着电子数字计算机的发生,1956年ward等人基本建设了实际可取的计算机潮流排序程序。
这样,就为日趋繁杂的大规模电力系统提供更多了极其有力的排序手段。
经过几十年的时间,电力系统潮流排序已经发展得十分明朗。
潮流排序就是研究电力系统稳态运转情况的一种排序,就是根据取值的运转条件及系统接线情况确认整个电力系统各个部分的运转状态,例如各母线的电压、各元件中穿过的功率、系统的功率损耗等等。
电力系统潮流排序就是排序系统动态平衡和静态平衡的基础。
在电力系统规划设计和现有电力系统运转方式的研究中,都须要利用电力系统潮流排序去定量的比较供电方案或运转方式的合理性、可靠性和经济性。
电力系统潮流计算分为离线计算和在线计算,离线计算主要用于系统规划设计、安排系统的运行方式,在线计算则用于运行中系统的实时监测和实时控制。
两种计算的原理在本质上是相同的。
实际电力系统的潮流技术主要使用pq水解法。
1974年,由scottb.在文献(@)中首次提出pq分解法,也叫快速解耦法(fastdecoupledloadflow,简写为fdlf)。
本设计就是使用pq水解法排序电力系统潮流的。
关键词:电力系统潮流排序pq水解法第一章概论1.1详述电力系统潮流计算是研究电力系统稳态运行情况的一种计算,它是根据给定的运行条件及系统接线情况确定整个电力系统各个部分的运行状态,如各母线的电压、各元件中流过的功率、系统的功率损耗等等。
电力系统潮流计算是计算系统动态稳定和静态稳定的基础。
在电力系统规划设计和现有电力系统运行方式的研究中,都需要利用电力系统潮流计算来定量的比较供电方案或运行方式的合理性、可靠性和经济性。
快速解耦法
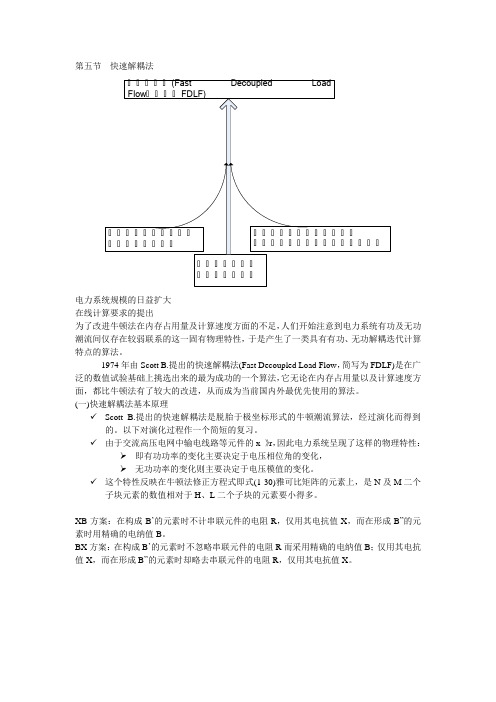
第五节快速解耦法电力系统规模的日益扩大在线计算要求的提出为了改进牛顿法在内存占用量及计算速度方面的不足,人们开始注意到电力系统有功及无功潮流间仅存在较弱联系的这一固有物理特性,于是产生了一类具有有功、无功解耦迭代计算特点的算法。
1974年由Scott B.提出的快速解耦法(Fast Decoupled Load Flow,简写为FDLF)是在广泛的数值试验基础上挑选出来的最为成功的一个算法,它无论在内存占用量以及计算速度方面,都比牛顿法有了较大的改进,从而成为当前国内外最优先使用的算法。
(一)快速解耦法基本原理✓Scott B.提出的快速解耦法是脱胎于极坐标形式的牛顿潮流算法,经过演化而得到的。
以下对演化过程作一个简短的复习。
✓由于交流高压电网中输电线路等元件的x 》r,因此电力系统呈现了这样的物理特性: 即有功功率的变化主要决定于电压相位角的变化,无功功率的变化则主要决定于电压模值的变化。
✓这个特性反映在牛顿法修正方程式即式(1-30)雅可比矩阵的元素上,是N及M二个子块元素的数值相对于H、L二个子块的元素要小得多。
XB方案:在构成B’的元素时不计串联元件的电阻R,仅用其电抗值X,而在形成B”的元素时用精确的电纳值B。
BX方案:在构成B’的元素时不忽略串联元件的电阻R而采用精确的电纳值B;仅用其电抗值X,而在形成B”的元素时却略去串联元件的电阻R,仅用其电抗值X。
系系系系系系系n-m-1系系系系系.系M 系系系系系H 系系系系系系系系系系系系系系系系系系系(系系10º--20º系系系系系系系系系系系系系系系 B ii 系系系ijB 2i iiU B ”系系系交流高压电网中输电线路等元件的x>>r电力系统呈现物理特性:有功功率的变化主要决定于电压相位角的变化 无功功率的变化则主要决定于电压模值的变化反映在牛顿法修正方程式雅可比矩阵的元素上,是N 及M 二个子块元素的数值相对于H 、L 二个子块的元素要小得多。
matlab快速解耦课程设计

matlab快速解耦课程设计一、课程目标知识目标:1. 理解Matlab软件在解耦控制中的应用,掌握其基本操作和函数使用。
2. 学习解耦控制理论,理解线性系统解耦的条件和步骤。
3. 了解解耦控制在实际工程中的应用案例,培养学生理论联系实际的能力。
技能目标:1. 能够运用Matlab软件进行系统建模、求解和解耦控制设计。
2. 学会使用Matlab进行数据分析,绘制相关图表,并解释结果。
3. 培养学生团队协作能力,通过分组讨论和项目实践,提高问题解决能力。
情感态度价值观目标:1. 培养学生对自动化控制领域的兴趣,激发其探索精神和创新意识。
2. 强化学生的实践操作能力,使其认识到理论与实践相结合的重要性。
3. 培养学生严谨的科学态度和良好的学习习惯,提高其自主学习和终身学习能力。
本课程针对高年级本科生或研究生,侧重于实际操作和理论应用。
根据课程性质、学生特点和教学要求,将课程目标分解为具体的学习成果,以便后续的教学设计和评估。
在教学过程中,注重理论与实践相结合,充分调动学生的主观能动性,培养具备实际操作能力和创新精神的优秀人才。
二、教学内容1. 解耦控制理论基础- 线性系统解耦条件与方法- 状态空间表达式与解耦矩阵- 相关课本章节:第三章线性系统解耦控制2. Matlab软件操作与使用- Matlab基本操作与界面介绍- 系统建模与仿真- 数据分析与图表绘制- 相关课本章节:第四章Matlab在解耦控制中的应用3. 实际案例分析与项目实践- 工程案例介绍:电机控制系统解耦设计- 分组讨论与协作- 项目实践:设计简单的解耦控制系统- 相关课本章节:第五章实际应用案例分析4. 教学进度安排- 理论学习:共计6课时- 软件操作与案例分析:共计4课时- 项目实践与总结:共计4课时教学内容根据课程目标进行选择和组织,确保科学性和系统性。
教学大纲明确教学内容安排和进度,结合课本章节进行讲解,注重理论与实践相结合,提高学生对解耦控制理论的理解和实际应用能力。
ETAP软件潮流计算方法

初始条件(Initial Condition)
在这部分中定义用于潮流计算的所有母线电压和相角的初始条件。
获取存档数据(Get Archived Data)
装有 ETAPS 存档回放的系统,所有的图形显示都是回放形式,点击该按钮可以将这些数据 传到您的图形显示中去并运行潮流分析。您会注意到:运行负荷,母线电压和编辑器都被存档数 据更新了。
欧特艾远东(南京)计算机技术有限公司
15-4
ETAP® PowerStation® 4.7
第 15 章
潮流分析(Load Flow Analysis)
PowerStation® 潮流分析程序计算母线电压,支路功率因数,电流,和整个电力系统的潮流。 该程序中允许进行调节平衡节点电压,不调节多个电源与等效电网和发电机的连接。它适用于辐 射型系统和环形系统。为获得较好的精确度有不同的方法可供选择。 本章为有些名词作了定义并解释了运行潮流分析时可能用到的工具。并说明了不同潮流计算 方法的理论背景。 潮流工具条部分解释了如何启动一个潮流计算,如何打开并查看输出报告,如何选择显示选 项。 潮流分析案例编辑器部分解释了如何创建一个新的分析案例,设定分析案例时需要哪些数 据,如何设定它们。显示选项部分解释了显示一些主要系统参数和在单线图中输出报告时的选 项,以及如何设定这些参数。 潮流计算方法部分列出了不同潮流计算方法的公式。这部分还将进 行比较收敛率,在不同系统参数和配置的情况下提高收敛率,还提供了一些选择相应计算方法的 技巧。计算需求数据部分描述了进行潮流计算所必需的数据以及在什么地方输入这些数据。最 后,潮流分析输出报告部分说明并解释了输出报告和他们的格式。
快速解耦法——精选推荐
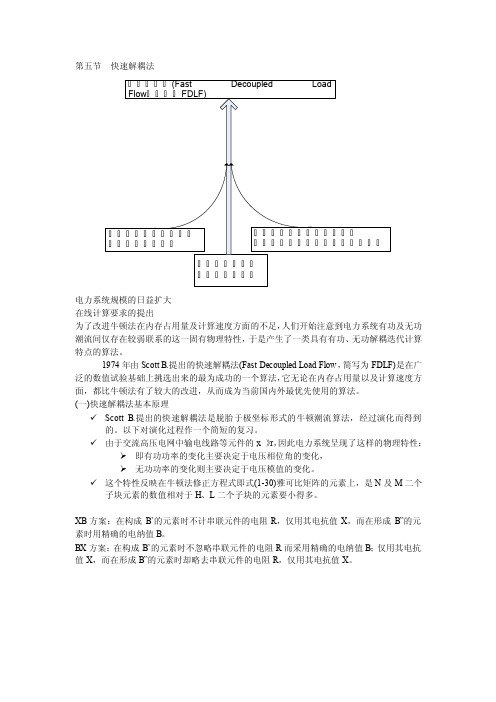
第五节快速解耦法电力系统规模的日益扩大在线计算要求的提出为了改进牛顿法在内存占用量及计算速度方面的不足,人们开始注意到电力系统有功及无功潮流间仅存在较弱联系的这一固有物理特性,于是产生了一类具有有功、无功解耦迭代计算特点的算法。
1974年由Scott B.提出的快速解耦法(Fast Decoupled Load Flow,简写为FDLF)是在广泛的数值试验基础上挑选出来的最为成功的一个算法,它无论在内存占用量以及计算速度方面,都比牛顿法有了较大的改进,从而成为当前国内外最优先使用的算法。
(一)快速解耦法基本原理✓Scott B.提出的快速解耦法是脱胎于极坐标形式的牛顿潮流算法,经过演化而得到的。
以下对演化过程作一个简短的复习。
✓由于交流高压电网中输电线路等元件的x 》r,因此电力系统呈现了这样的物理特性: 即有功功率的变化主要决定于电压相位角的变化,无功功率的变化则主要决定于电压模值的变化。
✓这个特性反映在牛顿法修正方程式即式(1-30)雅可比矩阵的元素上,是N及M二个子块元素的数值相对于H、L二个子块的元素要小得多。
XB方案:在构成B’的元素时不计串联元件的电阻R,仅用其电抗值X,而在形成B”的元素时用精确的电纳值B。
BX方案:在构成B’的元素时不忽略串联元件的电阻R而采用精确的电纳值B;仅用其电抗值X,而在形成B”的元素时却略去串联元件的电阻R,仅用其电抗值X。
系系系系系系系n-m-1系系系系系.系M 系系系系系H 系系系系系系系系系系系系系系系系系系系(系系10º--20º系系系系系系系系系系系系系系系 B ii 系系系ijB 2i iiU B ”系系系交流高压电网中输电线路等元件的x>>r电力系统呈现物理特性:有功功率的变化主要决定于电压相位角的变化 无功功率的变化则主要决定于电压模值的变化反映在牛顿法修正方程式雅可比矩阵的元素上,是N 及M 二个子块元素的数值相对于H 、L 二个子块的元素要小得多。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结束语
谢谢大家聆听!!!
22
✓就收敛特性而言,由于B’及B”在迭代过
程中保持不变,在数学上属于“等斜率” 法,因此本方法将从牛顿法的平方收敛特 性退化为线性收敛特性。于是,快速解耦 法达到收敛所需的迭代次数比牛顿法要多, 但由于每次迭代所需的时间远比牛顿法少, 所以总的计算速度仍有大幅度的提高。
✓下图表示了牛顿法和快速解耦法的典型收 敛特性。
✓快速解耦法也具有良好的收敛可靠性。除 了当网络中出现了在下面要进一步讨论的 元件R/X比值过大的病态条件以及因线路 特别重载以致两个节点间相角差特别大的 情况之外,一般均能可靠地收敛。
✓ 快速解耦法的程序设计较之牛顿法要来得简单。 因此,简单、快速、内存节省以及较好的收敛可 靠性形成了快速解耦法的突出优点,成为当前使 用最为普遍的一个算法。它不仅大量地用在规划 设计等离线计算的场合,而且由于其计算速度快, 也已经广泛地在安全分析等在线计算中得到应用。
Xij Rij2 Xij2
,BΒιβλιοθήκη '' iiBi0
ji
Xij Rij2 Xij2
式 中 : B i0 为 节 点 i 的 总 并 联 对 地 电 纳 , R ij和 X ij为 网 络 元 件
的 电 阻 和 电 抗 , j i表 示 求 和 符 号 后 标 号 为 j的 节 点 必 须 和
节 点 i直 接 相 连 , 但 不 包 括 ji的 情 况 。
式 中 : B i0 为 节 点 i 的 总 并 联 对 地 电 纳 , R ij和 X ij为 网 络 元 件
的 电 阻 和 电 抗 , j i表 示 求 和 符 号 后 标 号 为 j的 节 点 必 须 和
节 点 i直 接 相 连 , 但 不 包 括 ji的 情 况 。
Stott的快速分解法是计算实践的产物,为什么此法有很好 的收敛性在理论上人们进行了大量研究。但一直收效甚微, 直到1990年文献(@)做出了比较满意的解释,在一定程度上 阐明了快速分解潮流算法的收敛机理。
✓ 大R/X比值病态问题已成为快速解耦法应用中的 一个最大障碍。
✓解决这个问题的途径主要有以下两种:
1.对大尺/X比值支路的参数加以补偿,可以 分成串联补偿法及并联补偿法两种。
2.对算法加以改进
✓为了克服快速解耦算法在处理大R/X比值 伺题上的缺陷,许多研究工作立足于对原 有算法加以改进,这一类算法基本上还保 留了原来解耦算法的框架,但对修正方程
(2)不同于牛顿法的每次迭代都要重新形成雅可
比矩阵并进行三角分解,这里B’及B”是二个常
数阵,因此大大缩短了每次迭代所需的时间,
(3)雅可比矩阵J 不对称,而B’及B”都是对称
阵,为此只要形成并贮存因子表的上三角或下三 角部分,这样又减少了三角分解的计算量并节约 了内存。
✓由于上述原因,快速解耦法所需的内存量 约为牛顿法的60%,而每次迭代所需时间 约为牛顿法的1/5。
总结:牛顿法与快速解耦法的 主要区别
• (1)内存占用量方面,快速解耦法少,原因用两个阶 数几乎减半的方程组代替了牛顿法的方程组,雅可比矩 阵J不对称,而B’和B’’为对称阵;
• (2)计算速度方面,快速解耦法速度快,原因不同于 牛顿法的每次迭代都要重新形成雅可比矩阵并进行三角 分解,快速解耦法的B’和B’’为常数阵,只需形成一 次并三角分解,迭代过程中可反复应用,因而缩短了每 次迭代所需的时间;
式及其系数矩阵B’及B”的构成作出各种
不同的修改。
• XB方案和BX方案:
(1) XB模式
第一个里程碑
➢ 在计算B'时,忽略线路充电电容和变压器非标准变比
➢ 在计算B'时,略去串联元件的电阻
➢计算B' '时用精确值
具体计算公式为
Bij'
1
Xij
, Bii' Bij'
ji
ji
1 Xij
B '' ij
文献(@):
第三个里程碑
Monticelli A etal.Fast Decoupled Load Flow:Hypothesis, Derivations and Testing.IEEE Trans on Power Systems,1990, PWRS-5(4):1425-1431
✓ 为了解决大R/X比值病态问题,以上所述对元件 参数补偿以及对算法进行改进二种途径各有利弊。 使用补偿法要增加一个节点,当网络中大R/X比 值的元件数很多时将使计算网络的节点数增加很 多。而采用改进算法就不存在这个问题。但目前 已提出的一些改进算法并没有做到完全免除对元 件R/X比值的敏感性。当某个元件的R/X比值特 别高时,这些算法所需的迭代次数仍将急剧上升 或甚至发散。这种情况下对这些元件采用补偿方 法可能是一种好的选择。
(2) BX模式
第二个里程碑
➢在计算B'时,用精确值(忽略接地支路)
➢在计算B"时,略去串联元件的电阻,仅用电抗值
具体计算公式为
Bij '
X ij Rij 2 X ij 2
, Bii '
j i
X ij Rij 2 X ij 2
B '' ij
1 X ij
,
B '' ii
Bi 0
j i
1 X ij
快速解耦法
快速解耦法
(一)快速解耦法基本原理
(二)快速解耦法的特点和性能
✓ 快速解耦法和牛顿法的不同,主要体现在修正方 程式上面。比较两种算法的修正方程式,可见快 速解耦法具有以下特点:
(1)用解两个阶数几乎减半的方程组(n-1阶及nm-1阶)代替牛顿法的解一个2n-m-2阶方程组,显 著地减少了内存需量及计算量;
(三)元件大R/X比值病态问题
✓ FDLF是基于两个基本假设: R<<X 以及线路两端相 角差比较小。
✓ 当系统存在不符合这些假设的因素时,就会出现 迭代次数大大增加或甚至不收敛的情况。而其中 又以出现元件大R/X比值的机会最多,例如:
➢低电压网络
➢某些电缆线路
➢三绕组变压器的等值电路
➢通过某些等值方法所得到的等值网络等
