典型环节的单位阶跃响应
六种典型环节的阶跃响应曲线

六种典型环节的阶跃响应曲线
阶跃响应曲线是描述系统响应速度和稳定性的一种重要方法。
典型的
六种环节系统的阶跃响应曲线可分为惯性环节、比例环节、微分环节、积分环节、一阶惯性环节和二阶惯性环节。
下面分别介绍这六种环节
的阶跃响应曲线特点。
1. 惯性环节
惯性环节是指系统响应变化相对较慢,响应速度较慢,且响应幅值有
惯性的环节系统。
该系统的阶跃响应曲线呈现出逐渐上升并逐步趋于
平稳的特点。
2. 比例环节
比例环节是指系统的输出与输入成正比例关系的环节。
该系统的阶跃
响应曲线呈现出发生瞬间跳跃并在短时间内达到稳态值的特点。
3. 微分环节
微分环节是指系统输出与输入的导数成正比的环节。
该系统的阶跃响
应曲线呈现出瞬间跳跃并持续震荡的特点。
4. 积分环节
积分环节是指系统输出与输入的积分成正比的环节。
该系统的阶跃响应曲线呈现出发生跳跃后,曲线会不断向上弯曲,直到接近水平线的特点。
5. 一阶惯性环节
一阶惯性环节是指系统的输出与输入有一定的滞后性和时间常数的环节。
该系统的阶跃响应曲线呈现出逐渐上升并在一定时间后达到稳态值的特点。
6. 二阶惯性环节
二阶惯性环节是指系统的输出与输入存在两个相邻极点的环节。
该系统的阶跃响应曲线呈现出震荡过程中的不断衰减的特点。
综上所述,不同类型的环节系统响应速度和稳定性都有所不同,掌握不同环节的阶跃响应曲线特点有助于理解系统的动态特性和改善系统响应。
典型环节及其阶跃响应实验报告

典型环节及其阶跃响应实验报告学院:机械工程学院班级:过控一班姓名:***学号:***********实验内容 比例环节响应 实验人 卢世宝实验时间 教师签字学号后三位 由于本人的学号为416 所以取R=416电路传递函数响应函数 48.0)(0-==K t U实验波形图实验内容 积分环节模拟电路实验人 卢世宝实验时间 教师签字学号后三位 由于本人的学号为416 所以取R=416电路传递函数响应函数t t Tt U 740.01)(0-=-=实验波形图48.0)()(21-=-=R RS U S U i o SCS R S U S U i o /740.01)()(0-=-=实验内容 比例积分环节模拟电路实验人 卢世宝实验时间教师签字学号后三位 由于本人的学号为416 所以取R=416电路传递函数)1(1)()(001010CSR R R CS R CS R S U S U i +-=+-== 0.35+0.014 / S响应函数 t TK t U 1)(0+= = -0.35 – 0.73 t实验波形图实验内容 比例微分环节模拟电路 实验人 卢世宝 实验时间教师签字学号后三位由于本人的学号为416 所以取R=416电路传递函数)11()()(321210+•++-=CS R CS R R R R S U S U i =)122101(+⨯+-S S响应函数)330210210()(CR t e R R R R R R R t U -++-=t e 50088.0088.0(--+-=)实验波形图实验内容 惯性环节模拟电路 实验人 卢世宝实验时间 教师签字学号后三位由于本人的学号为416 所以取 R=416电路传递函数1)()(11+-=CSRRRSUSUi14.0343.0+-=S响应函数)1()(0TteKtU---=)1(343.025te---=实验波形图实验内容PID模拟电路实验人卢世宝实验时间教师签字学号后三位由于本人的学号为416 所以取R=416电路传递函数)1()()(020211001S C R R R S C R R R S Ui S U ++-≈ = - ( 13 + 10S )响应函数]})1(1[1{)(0232211102210021C R te C R C R C R C R t C R R R R t U --++++-=)1(5.1350t e t -+--=实验波形图实验一 典型环节及其阶跃响应一.实验原理和设计合理运用运算放大器本身所具有的基本特性(开环增益高、输入阻抗大、输出阻抗小等)用不同的电阻、电容组成不同的反馈网络来模拟各种典型环节。
典型环节与及其阶跃响应

实验一: 典型环节与及其阶跃响应一、实验目的1、掌握控制模拟实验的基本原理和一般方法。
2、掌握控制系统时域性能指标的测量方法。
二、实验仪器1、EL-AT-III 型自动控制系统实验箱一台2、计算机一台三、实验原理控制系统模拟实验采用复合网络法来模拟各种典型环节,即利用运算放大器不同的输入网络和反馈网络模拟各种典型环节,然后按照给定系统的结构图将这些模拟环节连接起来,便得到了相应的模拟系统。
再将输入信号加到模拟系统的输入端,并利用计算机等测量仪器,测量系统的输出,便可得到系统的动态响应曲线及性能指标。
若改变系统的参数,还可进一步分析研究参数对系统性能的影响。
四、实验内容构成下述典型一阶系统的模拟电路,并测量其阶跃响应1、比例环节的模拟电路及其传递函数G(S)= −R2/R12、惯性环节的模拟电路及其传递函数G(S)= −K/TS+1K=R2/R1T=R2C3、积分环节的模拟电路及传递函数G(S)=1/TST=RC4、微分环节的模拟电路及传递函数G(S)= −RCS5、比例+微分环节的模拟电路及传递函数G(S)= −K(TS+1)K=R2/R1T=R1C五、实验结果及分析(注:图中黄色为输入曲线、紫色为输出曲线)1、比例环节(1)模拟电路图:(2)响应曲线:2、惯性环节(1)模拟电路图:(2)响应曲线:(3)传递函数计算:实验值:X1=1029ms=1.029s=4TT=0.257sK=Y2/1000=2.017G(S)=-2.017/(0.257S+1) 理论值:G(S)=-2/(0.2S+1)结论:实验值与理论值相近。
3、积分环节(1)模拟电路图:(2)响应曲线:(3)传递函数计算:实验值:5000/(2110/2/2)=9.1G(S)=-9.1/S=-1/0.11S 理论值:G(S)=-1/0.1S结论:实验值与理论值相近。
4、微分环节(1)模拟电路图:(2)响应曲线:5、比例+微分环节(1)模拟电路图:(2)响应曲线:实验二:二阶系统阶跃响应一、实验目的1、研究二阶系统的特征参数,阻尼比ζ和无阻尼自然频率ωn 对系统动态性能的影响。
典型环节及其阶跃响应
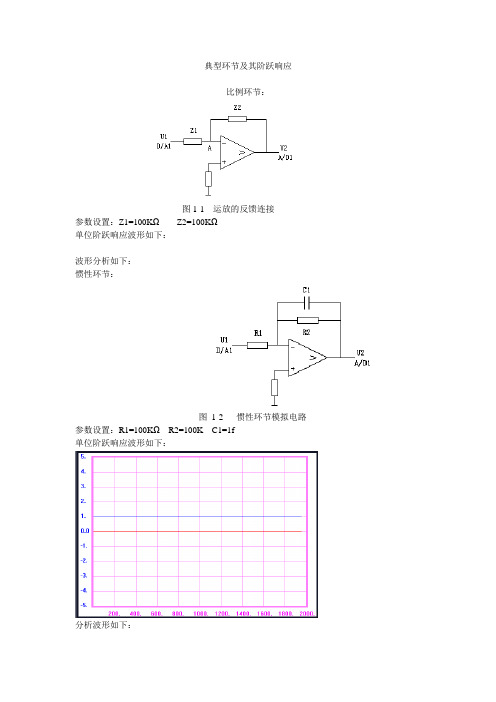
图1-1 运放的反馈连接 典型环节及其阶跃响应
比例环节:
参数设置:Z1=100K Ω Z2=100K Ω 单位阶跃响应波形如下:
波形分析如下: 惯性环节:
图 1-2 惯性环节模拟电路
参数设置:R1=100K Ω R2=100K C1=1f 单位阶跃响应波形如下:
分析波形如下:
积分环节
参数设置:R1=100K C1=1f
单位阶跃响应波形如下:
波形分析如下:
微分环节
微分环节模拟电路参数设置:C1=1f C2=0.01f R2=100K
单位阶跃响应波形如下:
波形分析如下:
比例微分环节
比例微分模拟电路
参数设置:R1=100K R2=100K C1=1f C2=0.01f 单位阶跃波形如下
波形分析如下:
比例积分环节
比例积分环节模拟电路
参数设置:R1=100K R2=200K C1=1f
单位阶跃波形如下
波形分析如下:
比例积分微分环节
比例积分微分模拟电路
参数设置1:R1=100K R2=200K C1=1f C2=0.1f 单位阶跃波形如下
单位阶跃波形如下
波形分析如下:。
《自动控制》一二阶典型环节阶跃响应实验分析报告
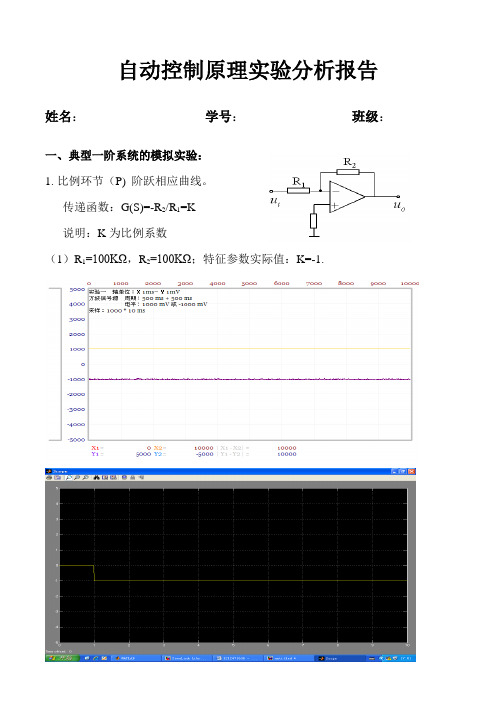
自动控制原理实验分析报告姓名:学号:班级:一、典型一阶系统的模拟实验:1.比例环节(P) 阶跃相应曲线。
传递函数:G(S)=-R2/R1=K说明:K为比例系数(1)R1=100KΩ,R2=100KΩ;特征参数实际值:K=-1.(2)(2)R1=100KΩ,R2=200KΩ;即K=-2.〖分析〗:经软件仿真,比例环节中的输出为常数比例增益K;比例环节的特性参数也为K,表征比例环节的输出量能够无失真、无滞后地按比例复现输入量。
2、惯性环节(T) 阶跃相应曲线及其分析。
传递函数:G(S)=-K/(TS+l) K=R2/R1 , T=R2C说明:特征参数为比例增益K和惯性时间常数T。
(1)、R2=R1=100KΩ , C=1µF;特征参数实际值:K=-1,T=0.1。
(2)、R2=R1=100KΩ , C=0.1µF;特征参数实际值:K=-1,T=0.01。
〖分析〗:惯性环节的阶跃相应是非周期的指数函数,当t=T时,输出量为0.632K,当t=3~4T时,输出量才接近稳态值。
比例增益K表征环节输出的放大能力,惯性时间常数T表征环节惯性的大小,T越大表示惯性越大,延迟的时间越长,反之亦然。
传递函数:G(S)= -l/TS ,T=RC说明:特征参数为积分时间常数T。
(1)、R=100KΩ , C=1µF;特征参数实际值:T=0.1。
(2)R=100KΩ , C=0.1µF;特征参数实际值:T=0.01。
〖分析〗:只要有一个恒定输入量作用于积分环节,其输出量就与时间成正比地无限增加,当t=T时,输出量等于输入信号的幅值大小。
积分时间常数T表征环节积累速率的快慢,T越大表示积分能力越强,反之亦然。
4、比例积分环节(PI) 阶跃相应曲线及其分析。
传递函数:G(S)=K( l+l/TS) K=-R2/R1, T=R2C说明:特征参数为比例增益K和积分时间常数T。
(1)、R2=R1=100KΩ , C=1µF;特征参数实际值:K=-1,T=0.1。
典型环节及其阶跃响应实验报告

典型环节及其阶跃响应实验报告哎呀,今天我们聊聊那个“典型环节及其阶跃响应”的实验报告,听起来有点高大上,其实呢,就是看看系统对刺激的反应,咱们就像是在观察一个小宝宝对糖果的反应,立刻就咧嘴笑了,那种欢快的感觉,简直让人心都化了。
你知道的,典型环节就像是一个经典的舞蹈动作,所有的机器、设备,都要围绕着它来转。
我们这次实验就像是给这个舞蹈加点新的花样,看看能不能让它更好看,更精彩。
说到阶跃响应,嘿嘿,想象一下,你在沙滩上,突然来了一波浪,直接把你淹没,那就是阶跃嘛!一开始,水面平静,突然间,哗的一声,浪花四溅。
这个实验就是模拟这种场景,我们用一个信号,给系统一个突如其来的“惊喜”,然后看它的反应。
像小狗听到门铃声那样,瞬间就警觉起来。
我们记录下它的表现,慢慢地分析,像是侦探在拼凑案件一样,越看越有意思。
实验开始的时候,大家都是一副严肃的样子,结果一搞起来,气氛就轻松了很多。
仪器啊,数据啊,真是让人眼花缭乱,搞得我都快晕了。
但没关系,我们的目标明确,简简单单就是想知道这个系统到底是个什么样的“角色”。
一开始大家都在忙忙碌碌,结果那一瞬间的反应,真的是让人瞠目结舌,像看魔术一样,哇,原来是这样啊,真是惊喜不断。
在记录数据的时候,大家开始窃窃私语,笑声不断,有人甚至模仿起了实验设备发出的声音,笑得我差点喷出来。
你看,这个实验不只是冰冷的数字,还有一堆有趣的故事,简直是给我们这个枯燥的学习过程加了不少料。
每当设备显示出一个新的数据点,大家都像中了彩票一样,欢呼雀跃,实验室里瞬间变成了欢乐的海洋。
随着数据的增加,分析起来也变得越来越有趣。
我们开始画图,连接那些数据点,像是在给一个故事编排情节,每一条线都承载着我们的期待。
你可能觉得这有点无聊,其实不然,这过程就像是在拼拼图,一块一块的拼出来,最终看到那个完整的图案,真的是成就感满满。
每当看到图上出现那条漂亮的曲线,大家都像喝了蜂蜜水一样甜。
最终,实验结束,大家都松了一口气,互相道了声辛苦。
六个典型环节的阶跃响应曲线详解

六个典型环节的阶跃响应曲线详解1. 引言在信号处理领域中,阶跃响应曲线是描述系统对单位阶跃输入信号的输出响应的一种常用方法。
通过分析阶跃响应曲线,我们可以了解系统的动态特性、稳态误差和稳定性等重要信息。
本文将详细探讨六个典型环节的阶跃响应曲线,以帮助读者更好地理解信号处理中的阶跃响应。
2. 一阶惯性环节让我们来讨论一阶惯性环节的阶跃响应曲线。
一阶惯性环节由一个惯性成分和一个系数组成,其传递函数可以表示为G(s) = k / (τs + 1),其中k为增益,τ为时间常数。
在阶跃输入信号下,一阶惯性环节的输出响应会经历一个指数衰减的过程。
初始阶段,响应曲线呈现出较大的上升斜率,接近输入信号的增量。
随着时间的推移,响应逐渐趋于稳定的平衡状态。
通过观察阶跃响应曲线的时间常数τ,我们可以推断系统的动态特性以及稳态稳定性。
3. 一阶积分环节接下来,我们将研究一阶积分环节的阶跃响应曲线。
一阶积分环节的传递函数可以表示为G(s) = k / s,其中k为增益。
与一阶惯性环节不同,一阶积分环节的阶跃响应曲线呈现出线性增长的特点。
输出信号随时间的增加而持续积分,并逐渐达到稳态。
在实际应用中,一阶积分环节常用于控制系统中,以改善系统的稳定性和对常数误差的补偿。
4. 一阶滞后环节第三个环节是一阶滞后环节,其传递函数可以表示为G(s) = k / (τs + 1),其中k为增益,τ为时间常数。
一阶滞后环节的阶跃响应曲线表现出一种惰性的特点。
初始阶段,响应曲线的上升斜率较小,逐渐接近输入信号的增量。
随着时间的推移,响应曲线逐渐逼近稳定的平衡状态。
一阶滞后环节常用于减小系统的动态响应,并提高稳态精度。
5. 二阶过阻尼环节接下来,我们将研究二阶过阻尼环节的阶跃响应曲线。
二阶过阻尼环节的传递函数可以表示为G(s) = k / (τ^2s^2 + 2ζτs + 1),其中k为增益,τ为时间常数,ζ为阻尼比。
二阶过阻尼环节的阶跃响应曲线表现出较小的震荡和较快的收敛特性。
自动控制原理实验-典型环节及其阶跃响应

6.比例+积分环节
四、实验结果及总结 1.各环节的响应曲线如上所示。
实验体会:通过这次实验,我们学会了如何构成典型环节的模拟电路及用计算机测量各典型环 节的阶跃响应曲线。在本次实验中出现了波形失真的情况,一开始找不到解决的办法,后
来我们不断的调节参数,才得到正确的波形,也明白了,只有理解并掌握了原理才能做出 正确的实验结果。
实验中心2013年11月4日年级专学院机电姓名学号业班实验课程名称成绩指导实验项目名称典型环节及其阶跃响应教师一实验目的二实验原理实验相关基础知识理论三实验过程原始记录程序界面代码设计调试过程描述等四实验结果及总结一实验目的1
广州大学学生实验报告
开课学院及实验室:实验中心
2013 年 11 月 4 日
图2-3 G(S)=-1/TS T=RC
4.微分环节的模拟电路及其传递函数如图2-4。
图2-4
G(S)=-RCS 5.比例+微分环节的模拟电路及其传递函数如图2-5。
图2-5
G(S)=-K(TS+1) K=R /R ,T=R C
21
2
6.比例Байду номын сангаас积分环节的模拟电路及其传递函数如图2-6。
图2-6
G(S)=K(1+1/TS) K=R /R , T=R C
惯性环节 8.连接被测量典型环节的模拟电路(图2-2)。电路的输入 U1接 A/D、D/A 卡的 DAl 输 出,电路的输出 U2接 A/D、D/A 卡的 ADl 输入。检查无误后接通电源。 9.实验步骤同4~7。
积分环节 10.连接被测量典型环节的模拟电路(图2-3)。电路的输入 Ul 接 A/D、D/A 卡的 DAl 输出,电路的输出 U2接 A/D、D/A 卡的 ADl 输入。检查无误后接通电源。 11.实验步骤同4~7。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二 典型环节的单位阶跃响应
一、实验目的
1、根据对象的单位阶跃响应特性,掌握和深刻理解几种典型环节的特性以及它们特性参数的含义。
2、研究对象传递函数的零极点对系统动态特性的影响。
3、学习Matlab 的基本用法
――求取阶跃响应、脉冲响应(step, impulse) ――基本做图方法(hold, plot)
二、实验内容 1、比例环节
求取K s G )(在不同比例系数K 下的单位阶跃响应,说明比例系数对系统动态过程的影响。
0.10.20.30.40.50.60.70.80.91
G(s)=K,在不同比例系数K 下的单位阶跃响应
Time (sec)
A m p l i t u d e
由上图可以看出:
因为G (s )=K ,所以被控对象是一个单纯的比例系统。
随着K 的增加,系统的终值是输入信号的K 倍。
2、一阶惯性环节
(1) 求取1
)(+=
Ts K
s G 的单位阶跃响应,其中放大倍数K =2,时间常数T =2。
1)(+=
Ts K
s G 的单位阶跃响应如下图:
0.20.40.60.811.2
1.41.61.82G(s)=2/(2s+1)的单位阶跃响应
Time (sec)
A m p l i t u d e
(2) 求取1
22
)(+=
s s G 的单位脉冲响应,可否用step 命令求取它的脉冲响应? 122
)(+=
s s G 的单位脉冲响应如下图:
0.10.20.30.40.50.6
0.70.80.91G(s)=2/(2s+1)的单位m 脉冲响应
Time (sec)
A m p l i t u d e
把传递函数乘以s 再求其单位阶跃响应,就可获得乘s 前的传递函数的脉冲响应。
如下图:
0.10.20.30.40.50.6
0.70.80.91G(s)=2*s/(2s+1)的单位m 阶跃响应
Tim e (sec)
A m p l i t u d e
(3) 围绕给定数值,K 和T 分别取大、中、小三种数值,求取此时对象的单位阶跃响应,说明这两个对象参数对系统过渡过程的动态特性与稳态特性的影响。
510
152025
0123456
78910
T 不变,K 改变时的系统阶跃响应
Time (sec)
A m p l i t u d e
00.5
1
1.5
2
2.5
3
3.5
4
K 不变,T 改变时的系统阶跃响应
Time (sec)
A m p l i t u d e
由以上两表可以总结出:随着K 的增大终值增大为原来的K 倍,而调节时间不变。
随着T
的增大调节时间也随之增大,但是终值不变。
两种情况下系统的稳态误差均为0,不存在超调量,上升时间均趋近于正无穷。
由此可以总结出,K 直接影响系统的终值,T 与系统的调节时间紧密相关,且均为正相关。
(4) 通过分析其中一个单位阶跃响应,反算出该对象的放大倍数和时间常数。
说明这样做的理由,理解对象的放大倍数和时间常数的物理意义。
根据K 与终值的正比例关系,找出图形中的终值就可以知道K 的值,之后因为点(T,0.632K )在图上,故作出图形找出纵坐标为0.632K 的点,该点所对应的横坐标就是所求的T 值
可以很明显的知道,K 表示系统的增益,而T 表示系统的时滞。
3、振荡环节(二阶系统)
根据传递函数2
222)(n
n n
s s s G ωζωω++=的单位阶跃响应。
(1)n ω=1,ζ分别取0、0.4、1.0、2; (2)ζ=0.5,n ω分别取0.2、0.6、1、1.4; 说明这两个特征参数对过渡过程的影响。
2468101214161820
00.20.40.60.811.2
1.41.61.82
ωn 不变,ζ改变时的系统阶跃响应
Time (sec)
A m p l i t u d e
102030405060
00.2
0.4
0.6
0.8
1
1.2
1.4
ζ不变,ωn 改变时的系统阶跃响应
Time (sec)
A m p l i t u d e
由以上两图和两表中所列数据进行分析可得:
n ω影响二阶系统过渡过程中的峰值时间,过渡时间,上升时间(在ζ不变的情况下,峰值
时间随n ω增大而减小,过渡时间随n ω的增大而减小,上升时间随n ω的增大而减小。
)
ζ影响几乎全部过渡过程指标,其中超调量,衰减比仅与ζ有关(超调量随着ζ的增大而
减小,衰减比随着ζ的增大而增大;在n ω不变的情况下,峰值时间随ζ增大而增大,过渡时间随ζ的增大而减小,上升时间随ζ的增大而减小。
)
n ω,ζ对系统的稳态误差均没有影响,且均为0.
4、滞后环节
对1
2)(2++=-s s e s G s
τ的系统,求取它的单位阶跃响应。
输入Matlab 文本见图1(%后为
注释,可不输入),修改滞后时间(transportation lag )Tao ,说明系统纯滞后环节的含义。
5
1015
00.5
1
1.5
2
2.5
transportation lag experiment
t(s)
y (t )
纯滞后环节:环节的的输出是经过一个延迟时间τ后,完全复现输入信号。
三、选作内容 1、积分环节
求取Ts
s G 1
)(
在不同积分时间常数T 下的单位阶跃响应,分析积分时间常数的作用。
0
500
10001500
02000
4000
6000
8000
10000
12000
14000
16000
Step Response
Time (sec)
A m p l i t u d e
由图可看出:积分环节强度随着T 的增加而减小
2、微分环节
在实际系统中,微分环节通常带有惯性,其传递函数为1
)(21+=s T s
T s G ,取T 2=1,T 1
为不同数值,分析微分时间常数T 1的作用。
00.511.5
2
2.5
不同微分常数的微分作用
Time (sec)
A m p l i t u d e
由上图可知:微分常数T 对于微分强度成正相关作用。
