第二章 流变学的基本概念
合集下载
Rheology(流变学基础)

二.非牛顿流动
实际上大多数液体不符合牛顿粘度定律, 实际上大多数液体不符合牛顿粘度定律,如高分子溶 胶体溶液、乳剂、混悬剂、软膏以及固液、胶体溶液、乳剂、混悬剂、软膏以及固-液的不均匀 体系的流动。把这种不遵循牛顿粘度定律的物质称为非牛 不遵循牛顿粘度定律的物质称为 体系的流动。把这种不遵循牛顿粘度定律的物质称为非牛 顿流体,这种物质的流动现象称为非牛顿流动 非牛顿流动。 顿流体,这种物质的流动现象称为非牛顿流动。 非牛顿流体的剪切速度D和剪切应力S的变化规律,经 非牛顿流体的剪切速度D和剪切应力S的变化规律, 作图后可得四种曲线的类型:塑性流动、假塑性流动、 作图后可得四种曲线的类型:塑性流动、假塑性流动、胀 形流动、触变流动。 形流动、触变流动。 对于非牛顿流体可以用旋转粘度计进行测定。 对于非牛顿流体可以用旋转粘度计进行测定。
对于这种粘弹性, 对于这种粘弹性,我们用弹性模型化的弹簧和把 粘性通过模型的缓冲器的复合型模型加以表示: 粘性通过模型的缓冲器的复合型模型加以表示: 麦克斯韦尔(Maxwell) (一)麦克斯韦尔(Maxwell)模型 福格特(Voigt) (二)福格特(Voigt)模型 (三)双重粘弹性模型 (四)多重粘弹性模型
胀性液体的流动公式: 胀性液体的流动公式: /η D= Sn /ηa n<1,为胀性流体; n<1,为胀性流体; 当n接近1时,流动接近牛顿流动。 接近1 流动接近牛顿流动。
(d)胀性流动
胀性流体的结构变化示意图
• 胀性流动的特点:没屈伏值;过原点;切应速度很小时, 胀性流动的特点:没屈伏值;过原点;切应速度很小时, 液体流动速度较大,当切应速度逐渐增加时, 液体流动速度较大,当切应速度逐渐增加时,液体流动速度 逐渐减小,液体对流动的阻力增加,表观粘度增加, 逐渐减小,液体对流动的阻力增加,表观粘度增加,流动曲 线向上弯曲。 线向上弯曲。 • 在制剂中表现为胀性流动的剂型为含有大量固体微粒的高 浓度混悬剂如50%淀粉混悬剂、糊剂等。 50%淀粉混悬剂 浓度混悬剂如50%淀粉混悬剂、糊剂等。
第2章 流变学的基本概念

u x u y u , 和 z x y z
分别表示各坐标 轴方向上的单位 伸长,即变形对 各坐标的变化率。
无穷小位移梯度张量
2.3.2 应变张量
根据矩阵运算法则,无穷小位移梯度张 量可分解为两部分:
1 u x u z ( + ) 2 z x 1 u y u z ( + ) y 2 z y u z 1 u z u y ( + ) 2 y z z 1 u x u y 1 u x u z 0 ( ) ( ) 2 y x 2 z x 1 u y u x u y 1 u y u z ) ( ) ( =E+W 2 x y y 2 z y 1 u u u z 1 u z u y x z ( ) ( ) 2 x z 2 y z z u x x du 1 u y u x ( + ) ds 2 x y 1 u u ( z + x) 2 x z 1 u x u y ( + ) 2 y x u y
2.2.3.2 张量的代数运算
1)张量相等 在同一坐标系中,如两张量的各个分量全部对 应相等,则两张量相等。
PQ
2)张量的加减 按矩阵方法,两张量对应分量相加减。
T PQ
标量、矢量和笛卡尔张量的定义
3)张量与标量的乘(除)
即把张量的各个分量分别乘以标量
P 11 T P P21 P 31 P 12 P22 P32 P P 13 11 P23 P21 P P33 31
第2章 流变学的基本概念
主要内容
2.1 流体形变的基本类型
2.2 标量、矢量和笛卡尔张量的定义 2.3 应力张量和应变张量 2.4 本构方程和材料函数
分别表示各坐标 轴方向上的单位 伸长,即变形对 各坐标的变化率。
无穷小位移梯度张量
2.3.2 应变张量
根据矩阵运算法则,无穷小位移梯度张 量可分解为两部分:
1 u x u z ( + ) 2 z x 1 u y u z ( + ) y 2 z y u z 1 u z u y ( + ) 2 y z z 1 u x u y 1 u x u z 0 ( ) ( ) 2 y x 2 z x 1 u y u x u y 1 u y u z ) ( ) ( =E+W 2 x y y 2 z y 1 u u u z 1 u z u y x z ( ) ( ) 2 x z 2 y z z u x x du 1 u y u x ( + ) ds 2 x y 1 u u ( z + x) 2 x z 1 u x u y ( + ) 2 y x u y
2.2.3.2 张量的代数运算
1)张量相等 在同一坐标系中,如两张量的各个分量全部对 应相等,则两张量相等。
PQ
2)张量的加减 按矩阵方法,两张量对应分量相加减。
T PQ
标量、矢量和笛卡尔张量的定义
3)张量与标量的乘(除)
即把张量的各个分量分别乘以标量
P 11 T P P21 P 31 P 12 P22 P32 P P 13 11 P23 P21 P P33 31
第2章 流变学的基本概念
主要内容
2.1 流体形变的基本类型
2.2 标量、矢量和笛卡尔张量的定义 2.3 应力张量和应变张量 2.4 本构方程和材料函数
流变学(二)

Polymer Rheology
第一章:流变学的基本概念
第二节 对应力的描述 一、张量的初步概念 1、张量的定义
BUCT
在场中某一点处,由于作用面方位不同而取得不同量 值的物理量称为张量,它既有大小,又有方向,还和 作用面的方位有关。 张量分量数目由阶数定,即: 张量分量数目=3n (数量30 、矢量31 、二阶张量32 )
Polymer Rheology
BUCT
第一章:流变学的基本概念
第二节 对应力的描述 二、应力的概念 1、作用在材料上的力
BUCT
r 体积力(远程力):重力、磁力等 单位:[力]∕[长度Δ ]2T
表面力(近程力):摩擦力、压力等 Kgf/cm2
2=Pa N/m ΔA
2、内力与应力
r ΔT r σ = lim ΔAc → 0 ΔA c
II ε =
BUCT
εx
1 γ yx 2
εx
1 III ε = γ yx 2 1 γ zx 2
Polymer Rheology
1 1 γ xy εy γ yz εx 2 2 + + 1 1 εy γ zy εz γ zx 2 2 1 1 γ xy γ xz 2 2 1 εy γ yz = ε 1 • ε 2 • ε 3 2 1 γ zy εz 2
τ 12 σ 22 − σ m τ 32
⎤ τ 23 ⎥ ⎥ σ 33 − σ m ⎥ ⎦
τ 13
应力张量
球应力张量
偏斜应力张量
1 σ m = (σ 11 + σ 22 + σ 33 ) 3
Polymer Rheology
第一章:流变学的基本概念
第二节 对应力的描述 五、应力张量的特殊形式 1、静压张量
第二章 流变学的基本概念

D、简单剪切 设流体的应力状态为,只有剪切分量ζxy 是常数,而 其它剪切分量为0,即在y=常数的平面上沿x方向受 到剪应力,按照应力对称原则,在x=常数的平面上 沿y方向也有剪切应力存在。如右图1.7所示。 此时应力可表示为
0 xy yx 0 0 0
第二章:流变学的基本概念
在流变学中讨论变形时,要研究变形时应力与
应变的关系,遵从胡克定律;讨论流动时,要研 究应力与应变速率的关系,遵从牛顿定律.下面 我们就从简单实验着手,讨论一些基本物理量.
2.1基本物理量
一、张量分析基础 1、张量概念 a、标量:只有大小,如温度、时间 b、矢量:既有大小又有方向,如位移、速度、 加速度、力 如空间坐标中,线段长度用OP表示,方向用 3 箭头表示,记为 OP a
二、应力及应力张量 1、应力的表示 物体在外力作用会产生流动和变形,但物体同时为抵抗 流动和变形,物体内部产生相应的应力。应力定义为材料 内部单位面积上的响应力,单位为Pa。
F lim s 0 s
2、应力张量 应力作用在材料的哪个面上.也是一个考虑的因素之一.因为 同样大小和方向的应用,如果作用面不同,材料也会发生不同 的变形所以应力也是一个张量. 由大小,方向及方向面的三 个因素决定.
偏应力张量的重要特征是对角线之和等于0。
应变 1.2.1 各向同性的压缩与膨胀(书10页)
1.2
a a b b c c a b c
.2.2
拉伸与单向压缩
l l l b b c c b c
ε为长度的分数增量,δ为侧边长的 分数减量.两者均称为应变.
流变学基础

由外部应力而产生的固体的变形,如除去其应力,则固 体恢复原状,这种性质称为弹性。
把这种可逆性变形称为弹性变形,而非可逆性变形称为 塑性变形。 流动主要表示液体和气体的性质。流动的难易与物质本 身具有的性质有关,把这种现象称为粘性。流动也视为一 种非可逆性变形过程。 实际上,某一种物质对外力表现为弹性和粘性双重特性 (粘弹性)。这种性质称为流变学性质,对这种现象进行 定量解析的学问称为流变学。
切力变稀体原因:1、由于剪切力作用使分子缠结解 开。2、由于大分子的长链结构,流动时,从不同
流速的液层中挣脱到同一流速层中去,而发生取
向。
(四)触变流动
当对某种体系进行搅拌时,由于其粘度下降,故流体易 于流动。但是,放臵一段时间以后,又恢复原来的粘性。 象这种随着切变应力的下降,其粘度下降的物质,即在等 温条件下缓慢地恢复到原来状态的现象称为触变性。
小分子流动与高分子黏性流动机理的区 别:
流动机理: 小分子的流动,简单来说是靠整个分子 的孔穴跃迁完成的。运动单元是整个分子。 在小分子液体内部,存在许多与小分子 尺寸相当的孔穴,在外力作用下,分子不断沿外 力方向跃迁填补前面的空穴,分子原来占有的位 臵成为新的空穴后,又让后面的分子跃入,从而 形成了液体的宏观流动。
(二)假塑性流动(高分子浓溶液)
随着σ值的增大粘度下降的流动现象称为假塑性流动。
(c)假塑性流动 式中,ηa ——表观粘度(apparent viscosity)。 假塑性流动的特点:没屈伏值;过原点;切应速度增大, 形成向下弯的上升曲线,粘度下降,液体变稀。
假塑性流体的结构变化示意图
式中,η—— 粘度或粘度系数,是表示流体粘性的物理常 数 。 单 位 为 泊 , 1 P= 0.1N· S · m-2,SI 单 位 中 粘 度 用 Pa· S或 Kg/(m· s)表示。粘度系数除以密度ρ得的值ν(ν =η/ρ)为 动力粘度(SI单位为㎡/S)。
流变学课件
力学状态:结晶态、无定形态和液晶态 聚合物液态:溶体、悬浮体、分散体和熔体 固体聚合物:均质态、取向态和多相态 无定形态聚合物:玻璃态、高弹态和粘流态; 结晶型聚合物有晶体和熔体
流变性能与 时间有关,
粘弹性
聚合物液态
聚合物溶体 悬浮体
1%以下的稀溶液,其性能不随时间 变化,属于牛顿流体 10%以上时,属于非牛顿的假塑性流 体,有剪切变稀的特征
线性粘弹性
非线性粘弹性
1.3.4聚合物流变行为的特性
(1)多样性
分子结构有线性结构、交联结构、网状结构等
分子链可以呈刚性或柔性
流变行为多种多样,固体高聚物的变形可呈 现线性弹性、橡胶弹性及粘弹性。聚合物溶液 和熔体的流动则可呈现线性粘性、非线性粘性 、塑性、触变性等
(2)高弹性 聚合物特有的流变行为
高达60%,失去流动性,属于非牛顿的 宾汉流体
更高浓度时,高交联度和高粘度,成为 冻胶和凝胶 (非牛顿)
剪切变稀的特征,假塑性非牛顿流体 剪切变稠特征,即膨胀性非牛顿流体
分散体
剪切速率较高时,假塑性非牛顿流体
在剪切速率不断提高时,膨胀性的非 牛顿流体
三维结构的凝胶体 ,宾汉流体
聚合物形态的转变 ——聚合物形态的热转变
➢聚合物流变性又是其加工成型的基础。粘度的温度依 赖性及剪切速率依赖性是确定加工工艺参数的重要依据
➢研究聚合物的流变行为为研究聚合物的分子结构提供 了重要的信息。
第二章 流变学的基本概念
流变学
变形 流动
应力与应变的关系 应力与应变速率的关系
应力、应变、应变速率
2.1 简单实验 (Simple experiments)
聚合物结构流变学和聚合物材料加工流变学,及其测定方 法和实际应用
第二章 流变学的基本概念
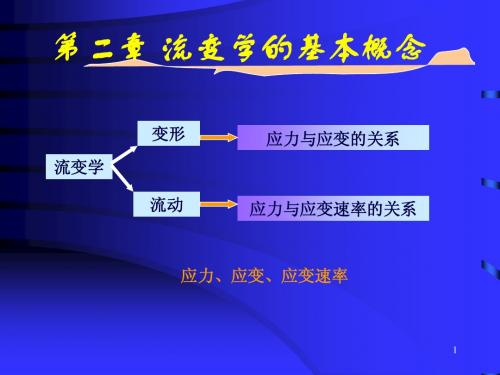
l′=l
b′=b c′=c V/V0=2Biblioteka =1+ <<1
=1- <<1
l l l
为长度的分数增量 为侧边的分数减量
5
b b c c b c
体积的分数变化
△V/V=[(1+)(1-)2-1]
由于<<1,<<1,故
△V/V≈-2
拉伸时,>1,<1,>0,>0, 压缩时,<1,>1,<0,<0,即长度缩小,截面增大
△V/V=3-1=(1+)3-1=3+32+3
由于<<1
△V/V≈3
△V/V是边长的分数变化的3倍
各向同性膨胀是均匀的变形(Homogeneous)。物体内 任何体积单元都变化3倍,当然物体不一定是立方柱体
4
2.2.2 拉伸和单向压缩 (Extension and uniaxial expension)
特点 材料均匀、各向同性,材料被施加的应力及发生的应变也 是均匀和各向同性,即应力、应变与坐标及其方向无关
2
2.2 应变(Strain)
2.2.1 各向同性的压缩和膨胀 (Isotropic compression and expansion)
a′=a b′=b
比 更常见 和更常用
c′=c
a b c 称为伸缩比(Stretch ratio) >1,膨胀, a b c <1,压缩, 3表示体积的变化
a a b b c c <<1 ,>0,膨胀,<0,压缩 1 3 a b c
体积变化量△V/V0,V0是原始体积,△V是体积之变化量
b′=b c′=c V/V0=2Biblioteka =1+ <<1
=1- <<1
l l l
为长度的分数增量 为侧边的分数减量
5
b b c c b c
体积的分数变化
△V/V=[(1+)(1-)2-1]
由于<<1,<<1,故
△V/V≈-2
拉伸时,>1,<1,>0,>0, 压缩时,<1,>1,<0,<0,即长度缩小,截面增大
△V/V=3-1=(1+)3-1=3+32+3
由于<<1
△V/V≈3
△V/V是边长的分数变化的3倍
各向同性膨胀是均匀的变形(Homogeneous)。物体内 任何体积单元都变化3倍,当然物体不一定是立方柱体
4
2.2.2 拉伸和单向压缩 (Extension and uniaxial expension)
特点 材料均匀、各向同性,材料被施加的应力及发生的应变也 是均匀和各向同性,即应力、应变与坐标及其方向无关
2
2.2 应变(Strain)
2.2.1 各向同性的压缩和膨胀 (Isotropic compression and expansion)
a′=a b′=b
比 更常见 和更常用
c′=c
a b c 称为伸缩比(Stretch ratio) >1,膨胀, a b c <1,压缩, 3表示体积的变化
a a b b c c <<1 ,>0,膨胀,<0,压缩 1 3 a b c
体积变化量△V/V0,V0是原始体积,△V是体积之变化量
第二章 流变学基本概念

剪切应变变形
应变 =
位移 间隙
剪切应变通常简称为应变 应变没有单位。因此人们采用 ‘% strain’ 或 ‘millistrain’ 采用应变的原因是它与几何形状无关
剪切应力
施加在单位面积上的力称为剪切应力
力 面积
=
N m2
1 N/m2 = 1 Pa
粘性流动
如果立方体是粘性液体,当我们施加一个力时,我们就 得到一个恒定的流动而不是一个形变 这个流动能够描述为应变随时间变化的函数关系
第三不变量:
2.4本构方程
本构方程又称流变状态方程,是联系应力张量和应变张量或应变 速率张量之间的关系方程,而联系的系数通常是材料常数,如粘 度、模量等. 从理论上讲:建立流体的本构方程是流变学最重要的任务,是将 计算方法引入流变学的关键。寻找合适的本构方程至今仍然是流 变学领域研究的一个热点。 从工程上讲:它是高分子加工过程复杂流动问题的工程分析基础。
单元表面作用力
图2-4中δS 是截面积,δF是作用力,v为法向单位矢量。P点应力σ的定义
2.3.1 应力张量
力:F 三个相互垂直面 力分解:F1, F2, F3 引入微元面和dS
得应力:T1,T2,T3
符号说明:
Txx 、 Tyy 、 Tzz 它们分别垂直于 x 、 y 、 z 轴垂直 的平面上称为法向应力分量。 Txy 、 Tyz 、 Txz 、 Tzx 、 Tyz 、 Tzy 均为某一平面上 平行的切应力方向, 第一个下标表示该分量作
Force, F
Constant velocity, v化速率称为剪切应变速率 (shear strain rate)或剪切速率(SHEAR RATE )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 简单实验
材料是均匀的,各向同性的, 而材料被施加的应力及发生的应变 也是均匀和各向同性的,即应力、 应变与坐标及其方向无关。
1.1 应变
1.1.1 各向同性的压缩和膨胀
y
c
x
b` b a c` a` 各向同性膨胀
z
a`=aα b`=bα c`=c α α-伸缩比
1
a`a b`b c`c 1 a b c 1
变化规律。
log
A t B a C
A:t 随 ↑ 而↑,
支化聚合物。如支化PE
B:t 与 无关: 聚合度低的线性高物:POM、PA-66 C:t 随 ↑而↓,
logŕ
高聚合度PP
拉伸流动中会发生链缠结, 拉伸黏度降低, 同时链伸展并沿 流动方向取向,分子间相互作用增加,流动阻力增加,伸展黏 度变大.拉伸黏度取决于这两个因素哪一个占优势.
t df / ds
df 为作用在表面上无限小面积ds上的力。在简单 实验中由于力是均匀的。 应力——材料单位面积受到的表面力作用
t f /s
1.2.1 应力的分量表示法和应力张量
应力的性质:应力的大小;方向;作用面。 应力的分量第1个下标表示作用面,第2个下 标表示应力的方向。 作用力的方向与作用面垂直,被称为应力的 法向分量, txx、 tyy 、 tzz。 作用力的方向与作用面平行,被称为应力的 切向分量,txy、 tyx 、 tzx、txz、tzy、tyz。
微晶的存在 起到交联的 作用
结晶性线形聚合物的拉伸模量与温度的关系 其形状与无定型聚合物类似,其区别是坪台区较宽,
且平台处的模量较高.
3.5 模量的分子量依赖性
低温时粘弹性主要决定于大分 子链的小链段的运动,而与大 分子链本身的尺寸基本上无关 。在高温时的粘弹性则涉及到 较大链段的复杂运动,以解开 缠绕并最后大分子链间相互滑 移 ,所以分子量对拉伸模量的 影响主要在高弹态和粘流态
拉伸黏度(t): 与液体弹性相关
定义:当聚合物熔体从任何形式的管道中流出,垂直于 流动方向的聚合物横断面积上所承受的拉应力与拉 伸应变速率的比值 与剪切过程中的黏度相似。只是速度梯度方向平行于 流动方向,
例如:吹塑成型中离开模口后的流动,纺丝中离开喷
丝口后的牵伸.
拉伸流动的研究在高分子材料加工工程中十分重要。在纤
弹性模量谱
聚合物与其他材料相比,其很明显的特点是它们的弹性模量 范围很宽(在室温时),相差3—4个数量级,玻璃态高聚物弹 性模量103—105MPa;橡胶态高聚物弹性模量0.1—1MPa.
玻璃态高聚物的弹性模量为103~105数量级, 如:酚醛塑料:E=104 MPa 密胺塑料:E=1.4×105 MPa 聚氯乙烯(硬质):E=4.9×103 MPa 橡胶和弹性体的模量为0.1~1 MPa,比玻璃 态聚合物 低3~4个数量级。
l ` l b` b c` c
b
A
l
λ称为伸长比 c` (Extension ratio) 1 , 1
x
f
V / V0 2
拉伸实验
1 , 1
l `l b b` c c` , l b c
V / V [(1 )(1 ) 2 1] 2
无定型线形聚合物的拉伸模量与分子量的关系(A<B<C) 分子量对模量的影响主要在高弹态和粘流态。分子量越高 ,橡胶坪台区越宽,但坪台区的模量数量级不因分子量增 大而变化,玻璃化温度也保持不变
3.6交联度对拉伸模量的影响
交联聚合物(橡胶)的拉伸模量与交联度的关系
随着交联度上升,橡胶坪台模量上升,交联度上升至形 成网状结构时,E几乎保持不变直到超过分解温度时发生分解 。同时玻璃化温度也随交联度提高而上升,而且玻璃化转变 区加宽(Tg升高)
y y面 x面 x z面 txx tyx
三个面上的应力分量: tx={txx, txy, txz} ty={tyx, tyy, tyz} tz={tzx, tzy, tzz}
z
应力的作用面
切向分量互等定律
用一个数组表示这三个面 上的应力矢量三个方向的应力 矢量:应力张量
t xy t yx t xz t zx t yz t zy
泊松比(Poison`s ratio)ν=δ/ε
泊松比
是材料横向应变与纵向应变的比值,也叫横向 变形系数,它是反映材料横向变形的弹性常数。
泊松比由法国科学家泊松最先发现并提出。他 在1829年发表的《弹性体平衡和运动研究报 告》.
空气的泊松比为0,水的泊松比为0.5
各向同性压缩
材料的应变为其体积变化分数,应力用压力P表示:
G,ν
E,ν
E,G
EG 3( 3G E )
E 2G (1 ) 3(1 2 ) 3(1 2 )
E
G
2(1 )G
E
E 2(1 )
E
G
E 1 2G
G
3 K 2G 6 K 2G
G
ν
ν
ν
E,G,K和 弹性常数不是相互独立的,而是相互 有一定的关系。因此表征一个材料的线性弹性只需其 中两个就足够. 一种常见的关系: =0.5或材料不可压缩时, E=3G E杨氏模量 K体积模量 G剪切模量 = / 泊松比
5)交联聚合物即使在温度比玻璃化温度高许多时仍符合 线弹性(如实验时有足够的时间使材料能达到平衡态) 。在时间较长的试验中出现粘弹性,应变较大时出现非 线性弹性,应力很高时可能断裂 6)线型和支链聚合物在温度比Tg高许多时在各向同性压缩 实验中仍符合线弹性。在其他实验(拉伸,剪切)中,会 出现线性粘性、非线性稳定流动、粘弹性等,如压力很大 ,可能出现非线性弹性
种是与拉伸应力几乎无关,如聚甲基丙烯酸甲酯、共聚甲醛、 尼龙66属于这种情况; 一种是随拉伸应力的增加而减小,如聚丙烯在应力为108 Pa 时的拉伸黏度只有应力为105 Pa时的1/5; 还有一种是随拉伸应力的增加而增加,如低密度聚乙烯。 目前尚无一种恰当的理论,能够预言拉伸黏度如此复杂的
维纺丝和薄膜吹塑过程中物料承受强烈的拉伸变形,流动过程 主要为拉伸流动。纤维纺丝过程为一维的单轴拉伸,薄膜吹塑 过程属二维的双向拉伸。在其它高分子材料加工过程,如压延、 挤出、注塑过程中也同样存在拉伸流动。
可以说,凡是弹性液体流经截面有显著变化的流道时,都有
拉伸流动存在。
高分子液体的拉伸黏度非常复杂。变化规律有多种类型:一
3.5.3 结晶聚合物的K
结晶聚合物的K(体积模量)与无定形聚合物接近,数 量级也是103 MPa。一般说,结晶度愈高,K愈大。
3.5.4 偏离线弹性的情况
当压力很高时会出现非线性弹性,在用各种加压速 度或频率时也会出现粘弹性,即时间依赖性
3.6 线弹性的适用范围
只有在变形很小时,下列材料才符合线弹性理论 1)陶瓷:绝大部分适用,只要应力小于破坏极限值 2)金属:在低于熔点的温度时或应变较大时,出现非 线性的弹性,应变很大时出现塑性和断裂;在精确的实 验中有些金属出现蠕变,即与时间有关的变形; 3)结晶体:原子、离子或分子晶体 4) 玻璃态材料:低于玻璃态温度时的聚合物;在 动态试验中可能出现粘弹性 (线性或非线性);应力 很高时出现塑性或断裂。
3.7 结晶度的影响
结晶性线性聚合物的拉伸模量与结晶度的关系
随着结晶度的提高,在低温没有影响,橡胶坪台 升高,结晶起交联作用。Tg不受结晶度影响
3.5 聚合物的体积模量
3.5.1 在高于Tg和Tm时聚合物的体积模量
3.5.2 玻璃态无定形聚台物的体积模量
低于玻璃化温度时的K比高于Tg时的最多大两倍,前面已经 看到,其他模量的变化则大得多
V / V (abc abc) / abc abc / abc 1
△V/V是边长的分数变化的3倍
V / V 3 1 (1 )3 1 3 3 2 3
1
V / V 3
1.1.2 单向拉伸和压缩
y
c b` f z l`
变形小
1
涉及聚合物分子中化学键的 拉伸、键角变化和键旋转, 不涉及链段的运动或整个分 子链的位移
变形无时间依赖性 变形在外力移除后完 全回复 无能量损失,(线性弹性称为能弹性 ) 应力与应变成线性关系
E
பைடு நூலகம்
3.3 弹性常数之间的关系
K, G K K
9 KG 3K G
第二章 流变学的基本概念
流变学基础
黏度:黏度是流体内部反抗这种流动的内摩擦阻力,与分子间的 缠绕程度和分子间的相互作用有关.单位: Pa· s 表观粘度又可以分为剪切黏度和拉伸黏度 剪切黏度(a) 表观黏度并不完全反映高分子不可逆形 变的难易程度.表 征流动性的好坏, 越大, 流动性越差, 越小 越好.
黏度与牛顿定律
资料: 假设液体或与其相同物质的各部分之间不能滑移,
所产生的阻力将正比于液体中各部分彼此分离的速
度。 ——牛顿(1687年《原理》)
:比例系数,称为黏度,表示流体流动阻力的大小。
单位:Pas 和 泊(P) :1P=0.1 Pas
对大多数高分子熔体而言,低速流动时近似遵循牛顿流动定 律,其黏度称零剪切黏度,也记为 ;流速较高时,剪切应 0 力与剪切速率之间不再呈直线关系
3 线形弹性
3.1 虎克定律与弹性常数
线性弹性体(Linear elastic solid)
– 长度变化正比于所施加的力,这种力学模式称为线弹 性(Linear elasticity)
3.1 虎克定律与弹性常数
虎克定律表示材料在受力时应力σ与应变ε之间存在线 性关系式σ=cε, 因此线性弹性也称为虎克弹性; 单向拉伸或压缩σ=Eε ,E为常数,以Euler的名字命 名,称为杨氏模量或拉伸弹性模量 其倒数D称为拉伸 柔量:E表示材料的刚性。E越大,产生相同的应变 需要的应力越大,即材料不易变形,刚性高
