材料力学典型题解
材料力学典型例题及解析 12.冲击问题典型习题解析

击构件瞬间的速度为 υ
,只须将前面(a)式右端改为
1 2
⋅
Pυ2 g
= Vε
,即可导出 kd
=
υ2 。 g∆st
(4)、前面推导过程中,冲击物的势能取为 Ep = P(h + ∆d ) ,一般情况下 ∆d << h ,可将其忽
略,取 Ep = Ph ,读者可仿照上面推导一下,并讨论忽略后对 kd 有什么影响。
所以本问题的动载荷因数为: kd
=
∆d ∆st
=1+
1+ 2h = 1+ ∆st
1+
2
× 440 ×10 −3 2 ×10 −3 m
m
= 22
讨论:(1)、在线弹性范围内,载荷、变形、应变、应力之间都是线性关系,也就是说,当
外载荷被放大 kd 倍,则变形、应力、应变也同样被放大 kd 倍。所以有σ d = kdσ st 。有了 kd 很
动能完全转化为橡皮筋的应变能。即 Ek = Vε 。
解:设小球离开木拍瞬间速度为υ ,则其动能 Ek
=
1 2பைடு நூலகம்
W g
υ 2 ;而橡皮筋被拉至最长时应变能
Vε
=
1 2
F ⋅ ∆L ,其中
F
为小球速度为零时橡皮筋所受拉力。由于假设橡皮筋为线弹性变形,
3
所以 F
=σ
A
=
Eε
A=
∆L L0
EA ,于是Vε
=
∆d
=
∆d ∆st
P 。定义
∆d ∆st
= kd 为动载荷因数,则有
Fd P
=
∆d ∆st
= σd σ st
材料力学试题及答案解析7套

材料力学试卷1一、结构构件应该具有足够的 、 和 。
(本题3分) 二、低碳钢拉伸破坏经历了四个典型阶段: 阶段、 阶段、 阶段和 阶段。
衡量材料强度的指标是 、 。
(本题6分) 三、在其他条件不变的前提下,压杆的柔度越大,则临界应力越 、临界力越 ;材料的临界柔度只与 有关。
(本题3分) 四、两圆截面杆直径关系为:123D D =,则12Z Z I I =;12Z Z W W =;12P P I I =;12P P W W =; (本题8分)五、已知构件上危险点的应力状态,计算第一强度理论相当应力;第二强度理论相当应力;第三强度理论相当应力;第四强度理论相当应力。
泊松比3.0=μ。
(本题15分)六、等截面直杆受力如图,已知杆的横截面积为A=400mm 2, P =20kN 。
试作直杆的轴力图;计算杆内的最大正应力;材料的弹性模量E =200Gpa ,计算杆的轴向总变形。
(本题15分)七、矩形截面梁,截面高宽比h=2b,l=4米,均布载荷q=30kN/m许用应力[]MPa100=σ,1、画梁的剪力图、弯矩图2、设计梁的截面(本题20分)。
八、一圆木柱高l=6米,直径D=200mm ,两端铰支,承受轴向载荷F=50kN,校核柱子的稳定性。
已知木材的许用应力[]MPa10=σ,折减系数与柔度的关系为:23000λϕ=。
(本题15分)九、用能量法计算结构B 点的转角和竖向位移,EI 已知。
(本题15分)材料力学试卷2一、(5分)图(a )与图(b )所示两个矩形微体,虚线表示其变形后的情况,确定该二微体在A 处切应变b aγγ的大小。
二、(10分)计算图形的惯性矩yz I I 。
图中尺寸单位:毫米。
三、(15分)已知构件上危险点的应力状态,计算第三强度理论相当应力;第四强度理论相当应力。
四、(10分)画图示杆的轴力图;计算横截面上最大正应力;计算杆最大轴向应变ε。
已知杆的横截面积A =400 mm 2,E =200GPa 。
材料力学考试典型题目

2
(4)
Fx 2 EIw Flx C1 (3) 2 2 3 Flx Fx EIw C 1x C 2 2 6 边界条件 x 0, w 0
x 0, w 0
(4)
将边界条件代入(3)(4)两式中,可得 C1 0 梁的转角方程和挠曲线方程分别为
C2 0
ql 2 q 3 EIw x x C 4 6
ql 3 q 4 EIw x x Cx D 12 24
边界条件x=0 和 x=l时, w
0
x
q
wmax B
梁的转角方程和挠曲线方程 A 分别为
A
l
B
q 2 3 3 (6lx 4 x l ) 24 EI qx w (2lx 2 x 3 l 3 ) 24 EI
FN 3 l3 -4 1.58 10 m uB ΔlCD Δl BC -0.3mm EA3
-4
Δl AD Δl AB Δl BC ΔlCD -0.47 10 mm
例题5 图示等直杆,已知直径d=40mm,a=400mm,材料的剪切弹性
模量G=80GPa,DB=1°. 试求:
x= l , M = 0
M 0
+
Mb l
梁上集中力偶作用处左、右两侧
FRA
A a
M
FRB
C b l B
横截面上的弯矩值(图)发生突变,其
突变值等于集中力偶矩的数值.此处 剪力图没有变化.
M /l
+ +
Mb l
Ma l
例题1 图示一抗弯刚度为 EI 的悬臂梁, 在自由端受一集中力 F 作用.试求梁的挠曲线方程和转角方程, 并确定其最大挠度 wmax 和最大转角 max w
工程力学材料力学-知识点-及典型例题
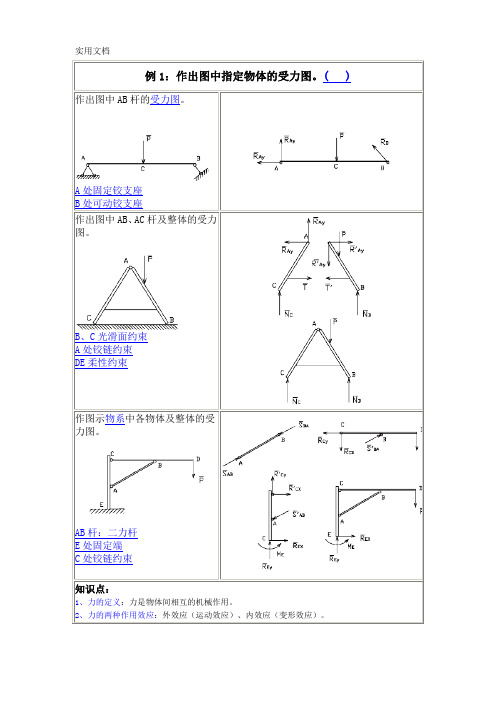
作出图中AB杆的受力图。
A处固定铰支座B处可动铰支座作出图中AB、AC杆及整体的受力图。
B、C光滑面约束A处铰链约束DE柔性约束作图示物系中各物体及整体的受力图。
AB杆:二力杆E处固定端C处铰链约束(1)运动效应:力使物体的机械运动状态发生变化的效应。
(2)变形效应:力使物体的形状发生和尺寸改变的效应。
3、力的三要素:力的大小、方向、作用点。
4、力的表示方法:(1)力是矢量,在图示力时,常用一带箭头的线段来表示力;(注意表明力的方向和力的作用点!)(2)在书写力时,力矢量用加黑的字母或大写字母上打一横线表示,如F、G、F1等等。
5、约束的概念:对物体的运动起限制作用的装置。
6、约束力(约束反力):约束作用于被约束物体上的力。
约束力的方向总是与约束所能限制的运动方向相反。
约束力的作用点,在约束与被约束物体的接处7、主动力:使物体产生运动或运动趋势的力。
作用于被约束物体上的除约束力以外的其它力。
8、柔性约束:如绳索、链条、胶带等。
(1)约束的特点:只能限制物体原柔索伸长方向的运动。
(2)约束反力的特点:约束反力沿柔索的中心线作用,离开被约束物体。
()9、光滑接触面:物体放置在光滑的地面或搁置在光滑的槽体内。
(1)约束的特点:两物体的接触表面上的摩擦力忽略不计,视为光滑接触面约束。
被约束的物体可以沿接触面滑动,但不能沿接触面的公法线方向压入接触面。
(2)约束反力的特点:光滑接触面的约束反力沿接触面的公法线,通过接触点,指向被约束物体。
()10、铰链约束:两个带有圆孔的物体,用光滑的圆柱型销钉相连接。
约束反力的特点:是方向未定的一个力;一般用一对正交的力来表示,指向假定。
()11、固定铰支座(1)约束的构造特点:把中间铰约束中的某一个构件换成支座,并与基础固定在一起,则构成了固定铰支座约束。
(2)约束反力的特点:固定铰支座的约束反力同中间铰的一样,也是方向未定的一个力;用一对正交的力来表示,指向假定。
()12、可动铰支座(1)约束的构造特点把固定铰支座的底部安放若干滚子,并与支撑连接则构成活动铰链支座约束,又称锟轴支座。
材料力学典型例题与详解(经典题目)
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
三种情况下所需石料的体积比值为 24∶19.7∶18,或 1.33∶1.09∶1。 讨论:计算结果表明,采用等强度石柱时最节省材料,这是因为这种设计使得各截面的正应 力均达到许用应力,使材料得到充分利用。 3 滑轮结构如图,AB 杆为钢材,截面为圆形,直径 d = 20 mm ,许用应力 [σ ] = 160 MPa ,BC 杆为木材,截面为方形,边长 a = 60 mm ,许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
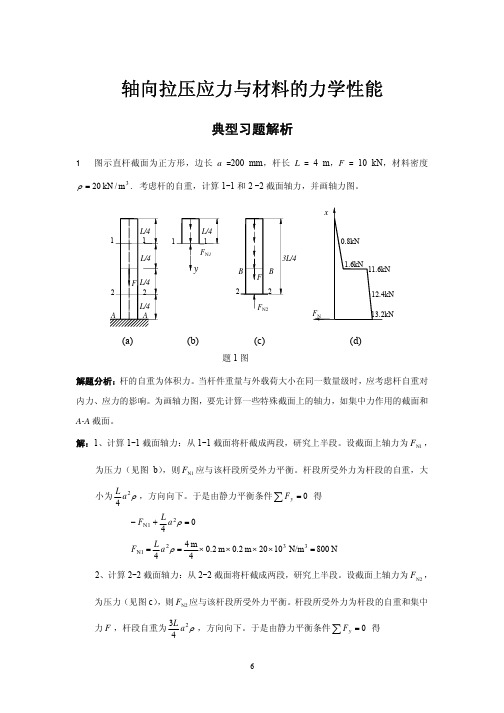
解:1、计算 1-1 截面轴力:从 1-1 截面将杆截成两段,研究上半段。设截面上轴力为 FN1 ,
为压力(见图 b),则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重,大
材料力学典型例题及解析7.应力应变状态典型习题解析

应力、应变状态分析典型习题解析1 已知矩形截面梁,某截面上的剪力F S =120 kN 及弯矩m kN 10⋅=M 。
绘出表示1、2、3及4点应力状态的微体,并求出各点的主应力。
b = 60 mm ,h = 100 mm 。
解题分析:从图中可分析1、4点是单向应力状态,2点在中性轴上为纯剪切应力状态,31取平行和垂直与梁横截面的六个平面,构成微体。
则各点处的应力状态如图示。
2、梁截面惯性矩为点微体上既有正应力又有切应力。
解:、画各点处微体的应力状态图计算各点处主应力4843333m 1050012m 10100(106012−−−×=×××==)bh I z 1点处弯曲正应力(压应力)MPa 100Pa 10100m10500m 1050m N 101064833−=×=×××⋅×==−−z I My σ1点为单向压缩受力状态,所以021==σσ,MPa 1003−=σ2点为纯剪切应力状态,MPa 30Pa 1030m10100602N1012036263=×=×××××=−τ(向下)容易得到,MPa 301=σ,02=σ,MPa303−=σ3点为一般平面应力状态弯曲正应力MPa50Pa 1050m 10500m 1025m N 101064833=×=×××⋅×==−−z I My σ弯曲切应力σ14τ2F S =120 kN题图1中性轴324hστ25 mm 31b M =10 kN·mσ3150 mm 1MPa 5.22Pa 1050.22m10500m 1060m 105.372560N 101206483393*S =×=××××××××==−−−zz bI S F τMPa6.8MPa6.58Pa)10522()2Pa 1050(2Pa 1050)2(22626622minmax −=×+×±×=+−±+=x y x yx τσσσσσσ所以 MPa 6.581=σ,02=σ,MPa 6.83−=σ4点为单向拉伸应力状态,拉伸正应力的大小与1点相等。
材料力学典型例题及解析 3.扭转典型习题解析

的切向内力所形成的力偶矩将由哪个力偶矩来平衡?
A M
B
A
M
B
C
z
D
A
(a)
C
dρ
ρ
R
(c)
D
题2图
BC Dx
(b)
θ dθ
(d)
解题分析:由切应力互等定理可知截面ABCD上的切向内力分布及其大小。该截面上切向内
力形成一个垂直向上的力偶矩。在图b中,左右两个横截面上的水平切向内力分量形成垂直
于截面ABCD的竖直向下的力偶矩,正好与截面ABCD上切向内力的合力偶矩平衡。
应力相等的条件下,试确定空心轴的外径,并比较实心轴和空心轴的重量。
解题分析:用空心轴代替实心轴,须保证二者强度相同。根据强度条件可求出D值,再用面
积比得出重量比。
解:1、根据两轴切应力相等的条件,确定空心轴外径
Tmax = Tmax = [τ ] WP实 WP空
πd 3 = πD3 (1 − α 4 ) 16 16
解得 D = 107.7 ×10−3 m = 107.7 mm
δ = D − d = 107.7mm −100mm = 3.85 mm
2
2
比较可知,两种设计的结果非常接近。
讨论: 当 δ ≤ R0 /10 时,即认为是薄壁圆管,可以直接使用薄壁管扭转公式。
2 图示受扭圆杆,沿平面ABCD截取下半部分为研究对象,如图b所示。试问截面ABCD上
4
即在强度相同条件下,空心轴可以节约近30%的材料。
讨论:在实际工程中常用空心圆轴代替实心圆轴,在保障安全运行的前提下,可以节约材料。
5 已知钻探机杆的外径D = 60 mm,内径d = 50 mm,功率P = 7.46 kW,转速n =180 r/min, 钻杆入土深度l = 40 m,G = 80 GPa,[τ]= 40 MPa。设土壤对钻杆的阻力是沿长度均匀分布 的,试求:(1) 单位长度上土壤对钻杆的阻力矩M;(2) 作钻杆的扭矩图,并进行强度校核; (3) 求A、B两截面相对扭转角。 解题分析:根据题意,为圆轴扭转问题。土壤对钻杆的阻力形成扭力矩作用在钻杆上,并沿
材料力学力法典型例题解

l
q
RB
B
l q
X1
B Δ1F
B δ11
1
Example 2 .画图示钢架旳弯矩图,EI=const .
P
a
B
A
CP B
A
a
CP
a
B
C
B
C
X1
M
1
M
A
A
Pa
a
解 : 1)选图示相当系统(:一次超静定)
2)力法方程:
X 0
11 1
1P
3)利用图乘法求系数:
a
P
a
B
A
a
C
P
a
B
C
B
C
M
1
M
A
A
PPal
X1
2)力法方程
F
X 0
11 1
1P
3)图乘法求系数
11
2 EI
(1 2
aa
2 3
a)
2a3 3EI
1P
2 EI
(1 2
a
Fa
2 3
a)
a a
2Fa3
M
3EI
4)解得:
1
C
X1
1P
11
F
1
C
Fa
X1=1 Fa
F
1
M
F
F1 C
F
Example 1 . 求RB (EI=const.).
解: 1)选图示相当系统 (一次超静定)
B
CP
P
P
a
a
X1
a a
X1 1
A
Pa
解:1)选图示静定基及相当系统
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1轴向拉伸与压缩例1-1 如图所示的等截面直杆,受轴向力F 1=15kN ,F 2=10kN 的作用。
试分别求出杆件1-1、2-2截面的轴力,并画出轴力图。
F 2F 2C 22 22F 111 11B F 1AF RF RF N1F 1F N2F R F N10kN5kN图1-1解:(1)外力分析 先解除约束,画出杆件的受力图。
120,0xR FF F F = -+=∑得:()121510kN 5kN R F F F =-=-=(2)内力分析 外力F R 、F 1、F 2将杆件分为AB 段和BC 段,在AB 段,用1-1截面将杆件截分为两段,取左段为研究对象,右段对截面的作用力用F N1来代替。
假定内力F N1为正,列平衡方程10,0xN R FF F = +=∑得:15kN N R F F =-=-负号表示F N1的方向和假定方向相反,截面受压。
在BC 这一段,用任意2-2截面将杆件分为两段,取左段为研究对象,右段对左段截面的作用力用F N2来代替。
假定轴力F N2为正,有平衡方程2100xN R FF F F = +-=∑得: ()21515kN N R F F F =-+=-+=10kN (3)画轴力图由以上例题可以总结出求截面轴力的简捷方法:杆件任意截面的轴力F N (x )等于截面一侧所有外力的代数和。
即1nN i i F F ==∑,外力背离该截面的时取正,指向该截面时取负。
例1-2 如图所示为正方形截面阶梯杆,受力及尺寸如图所示。
试分析杆上1截面处和2截面处的正应力。
FF2hh12(a )FFF N 11122N hh σ==F F F N 1222244N h h σ==F F(b ) 图1-2解:先求出杆两截面处的轴力F N 1和F N 2,在用截面上的轴力除以相应的截面面积,如图(b )所示,不难求出σ1=F/h 2,σ2=F/(4h 2)。
例1-3 如图所示,斜杆AB 为直径d =20mm 的钢杆,载荷Q =15kN 。
求此时斜杆AB 横截面上的正应力。
F AB F ABBAdAC0.8m1.9m0.5mB QBQCF CyF CxF ABαα图1- 3解:BC 杆受力分析如图1-3所示。
()0CMF =∑, (1.9sin )(1.90.5)0AB F a Q --=所以 1.41.9sin AB Q F a=又sin 0.388a ==所以1.41528.5kN 1.90.388AB F ⨯==⨯又因斜杆的内力(轴力)为28.5kN N A B F F == 由此得出AB 杆横截面上的应力为:228.5kN90.76MPa (20mm)4N F A == 例1-4 一构件如图所示,已知:F 1=30kN ,F 2=10kN ,A AB =A BC =500mm 2,A CD =200mm 2,E =200GPa 。
试求:(1)各段杆横截面上的内力和应力;(2)杆的总伸长。
BCD F 1F 2A100 100 100(a )BCDF 1F 2 1 F 112 2F N 2F N 1xF N30kN20k N(b )图1-4解:(1)整个杆共在三处受外力,每两各外力作用点之间的轴力都相等(即AB 段内轴力是一定值,BD 段内轴力也是一定值)。
所以只要在AB 段内任求一截面1-1处的轴力F N1,就知道整段AB 上的内力。
同样只要在BC 段内任求一截面2-2处的轴力就可知道整段BC 上的内力。
整杆的内力分布如图1-4所示。
虽然BD 段上的轴力都等于30kN ,但是由于BC 段和CD 段横截面不等。
所以它们的应力也不等。
320kN 2010N40MP 500mm 500mm NAB AB AB F A σ⨯==== 330kN 3010N 60MP 500mm 500mm NBC BC BC F A σ⨯==== 330kN 3010N 150MP 200mm 200mmNCD CDCD F A σ⨯==== (2)虽然杆对于整杆AD 不满足胡克定律的适用条件,但AB 段、BC 段和CD 却能分别满足胡克定律,因此,我们可按胡克定律分别求AB 、BC 、CD 三段杆的伸长量,然后相加得到杆AD 的总伸长量。
又根据公式(3-2)和(3-6)可推得:L L L Eσε∆==所以40MPa100mm 0.02mm 200GPaABAB AB L L Eσ∆=⨯=⨯= 60MPa100mm 0.03mm 200GPaBCBC BC L L Eσ∆=⨯=⨯= 150MPa100mm 0.075mm 200GPaCDCD BC L L Eσ∆=⨯=⨯= 0.02mm 0.03mm 0.075mm 0.125mm AB BC CD L L L L ∆=∆+∆+∆=++=例1-5 如图所示为某铣床工作台进给油缸图,缸内工作油压P =2MPa ,油缸内径D =75mm ,活塞杆直径d =18mm ,已知活塞杆材料的许用应力[σ]=50MPa ,试校核该活塞杆的强度。
FPDd图1-5解:(1)求活塞杆的轴力22221π()π(7518)244N D d F pA p --===⨯(2)按强度条件校核222π(7518)24MPa 32.6MPa π184N F Aσ-⨯===⨯ 显然σ<[σ]。
所以活塞杆的强度足够。
例1-6 如图6所示为一钢木结构。
AB 为木杆,其截面A 1=10×103mm 2,许用压应力[σ]1=7MPa ;BC 为钢杆,其截面积A 2=600mm 2,许用应力[σ]2=160MPa 。
(1)若吊起重物为45kN ,试校核AB 和BC 杆的强度;(2)试求B 处可吊的最大载荷W ;(3)若吊起重物为50kN ,则两杆的截面面积至少为多少才能保证两杆能安全的工作?CA 拉杆 30︒B WN BC N AByB xW(a ) (b )图1- 6解:(1)AB 、BC 为二力杆件,取B 为研究对象,受力分析如图1-6(b )所示。
由平衡条件可求得N BC 及N AB 与载荷W 的关系为0yF=∑,sin300BC N W ︒-=由此得2245kN 90kN sin30BC WN W ===⨯=︒0xF=∑c o s 30A B B CN N-︒=由此得cos302 1.73245kN 77.94kN AB BC N N W =︒===⨯= 则132177.94kN7.8MPa 1010mmAB N A σ===⨯22290kN150MPa 600mm BC N A σ=== 因为[]117.8MPa 7MPa σσ=>=,[]22150MPa 160MPa σσ=<=所以AB 杆不满足强度要求,BC 杆满足强度要求。
(2)由(1)可得N BC 及N AB 与载荷W 的关系为2BC N W =AB N =又117MPa AB N A σ== 所以3340.410N 40.4kN W =⨯=同样2222160MPa 600mm BC N WA σ==≤ 160600N 48kN 2W ⨯=≤因此,为了保证此结构的安全,B 处可吊的最大许可载荷W =40.4kN 。
(3)根据强度公式[]111ABN A σσ=≤可得 []42111.210mm ABN A σ==⨯≥同样可得[]2222250k N625m m160M P a 160M P aBCN W A σ⨯===≥2剪切与挤压例2-1 试校核如图2-1所示中齿轮与轴的平键连接的强度。
已知装齿轮处轴的直径d =48mm ,A 型平键的尺寸为b =14mm ,h =9mm ,L =45mm ,传递的转矩M T =l81481 N·mm ,键的许用切应力[τ]=60MPa ,许用挤压应力[σ jy ]=130MPa 。
hbdd +t 1d -t t t 1(a ) (b )bR=b /2A 型h L(c )d O mM Tbmh /2M TFLl(d ) (e )图 2- 1解:由于键是A 型键,其形状如图2-1(c )所示。
此类型键的两个圆头与轮毂上的键槽并不接触,所以该键的有效工作长度为l L b =-。
(1)以键和轴整体为研究对象,其受力分析如图2-1(d )所示。
求键所受的力。
()0O M F =∑,即02d F T ⨯-=,所以221814817561.7N 48T F d ⨯=== 键连接的破坏可能是键沿m -m 截面被切断及键与键槽工作面间的挤压破坏。
则用截面法可求得剪切力和挤压力为7561.7N s jy F F F ===。
(2)校核键的强度计算如下:键的剪切面积()s A bl b L b ==-,挤压面积为()22jy h h A l L b ==-[]7561.7MPa 17.4MPa 60MPa 14(4514)s s F A ττ===<=⨯- ()7561.7MPa 54.2MPa 945142jy jy jy jyF A σσ⎡⎤===<⎣⎦- 键的剪切和挤压强度均满足要求。
例2-2 如图2-2所示为螺栓连接,已知钢板的厚度σ = 10mm ,设上下两钢板与螺栓实际接触高度近似都等于钢板的厚度。
螺栓的许用切应力[σ]=100MPa ,许用挤压应力[σjy ]= 200MPa ,F=28kN ,试选择该螺栓的直径。
FFFδd 0Fδd 0m m(a ) (b )图2-2解:(1)分析破坏形式从图可以看出,螺栓的破坏可能是沿m -m 截面被切断及与孔壁间的挤压变形。
(2)求切力和挤压力。
用截面法可求得28kN Q jy F F F ===(3)按剪切强度条件设计螺杆配合直径d 0018.9mm d = (4)按挤压强度条件设计螺杆配合直径d 00jy jy jy F A d δσ=⎡⎤⎣⎦≥028000mm 14mm 20010jy jy F d σ==⨯⎡⎤δ⎣⎦≥若要螺栓同时满足剪切和挤压强度的要求,则其螺杆配合直径应为d0=18.9mm。
按此直径从设计手册中选用M18的六角头铰制孔用螺栓,其螺杆配合直径d0=19mm。
3扭转例3-1 如图3-1所示圆截面杆各截面处的外力偶大小分别为1e M =6M ,2e M =M ,3e M =2M ,4e M =3M 。
求杆在截面1-1、2-2、3-3处的扭矩。
(a )M e 12 M e 2 M e3 M e 41 3 A2 B 13 C DM e 1 M e 2 1 T 1xA B 1 (b )(c )(d )M e 1 2 T 2xA 2 M e 1 M e 2M e 3T 3xA BC(e )T 6M 5M3M+xO图3-1解:由截面法,沿各所求截面将杆件切开,取左段为研究对象,并以T 1、T 2、T 3表示相应截面上的扭矩。
