信号与系统课后习题参考答案
信号与系统 陈后金 第二版 课后习题答案(完整版)
（1） f (t) = 3sin 2t + 6 sinπ t
（2） f (t) = (a sin t) 2
（8）
f
(k)
=
cos⎜⎛ ⎝
πk 4
⎟⎞ ⎠
+
sin⎜⎛ ⎝
πk 8
⎟⎞ ⎠
−
2
cos⎜⎛ ⎝
πk 2
⎟⎞ ⎠
解：（1）因为 sin 2t 的周期为π ，而 sin πt 的周期为 2 。
显然，使方程
−∞
0
2-10 已知信号 f (t) 的波形如题 2-10 图所示，绘出下列信号的波形。
f (t)
2
1
−1 0
t 2
题 2-10 图
（3） f (5 − 3t) （7） f ′(t) 解：（3）将 f (t) 表示成如下的数学表达式
（5） f (t)u(1 − t)
由此得
⎧2
f
(t)
=
⎪ ⎨ ⎪ ⎩
f (t)u(1− t) 2
1
0.5
t
−1 0
1
（7）方法 1：几何法。由于 f (t) 的波形在 t = −1处有一个幅度为 2 的正跳变，所以 f ′(t) 在 此处会形成一个强度为 2 的冲激信号。同理，在 t = 0 处 f ′(t) 会形成一个强度为 1 的冲激信 号（方向向下，因为是负跳变），而在 0 < t < 2 的区间内有 f ′(t) = −0.5 （由 f (t) 的表达式可
第 1 页 共 27 页
《信号与系统》（陈后金等编）作业参考解答
（2）显然，该系统为非线性系统。 由于
T{f (t − t0 )}= Kf (t − t0 ) + f 2 (t − t0 ) = y(t − t0 )
信号与系统课后习题参考答案
1试分别指出以下波形是属于哪种信号？题图1-11-2 试写出题1-1 图中信号的函数表达式。
1-3 已知信号x1(t)与x2(t)波形如题图1-3 中所示，试作出下列各信号的波形图，并加以标注。
题图1-3⑴x1(t2)⑵ x1(1 t)⑶ x1(2t 2)⑷ x2(t 3)⑸ x2(t 2) ⑹x2(1 2t)2⑺x1(t) x2( t)⑻x1(1 t)x2(t 1)⑼x1(2 t) x2(t 4)21- 4 已知信号x1(n)与x2 (n)波形如题图1-4中所示，试作出下列各信号的波形图，并加以标注。
题图1-4⑴x1(2n 1) ⑵ x1(4 n)⑶ x1(n)2⑷ x2 (2 n)⑸ x2(n 2) ⑹ x2(n 2) x2( n 1)⑺x1(n 2) x2(1 2n)⑻x1(1 n) x2(n 4)⑼ x1(n 1) x2(n 3)1- 5 已知信号x(5 2t )的波形如题图1-5 所示，试作出信号x(t)的波形图，并加以标注。
题图1-51- 6 试画出下列信号的波形图：1⑴ x(t) sin( t) sin(8 t)⑵ x(t) [1 sin( t )] sin(8 t)21⑶x(t) [1 sin( t)] sin(8 t)⑷ x(t) sin( 2t )1-7 试画出下列信号的波形图：⑴ x(t)1 e t u(t) ⑵ x(t) e t cos10 t[u(t 1) u(t 2)]⑶ x(t)(2 e t)u(t)⑷ x(t) e (t 1)u(t)⑸ x(t)u(t22 9) ⑹ x(t)(t2 4)1-8 试求出以下复变函数的模与幅角，并画出模与幅角的波形图1j2 ⑴ X (j ) (1 e j2)⑵ X( j1 e j4⑶ X (j ) 11 ee j ⑷ X( j )试作出下列波形的奇分量、偶分量和非零区间上的平均分量与交流分量。
题图 1-10形图。
题图 1-141-15 已知系统的信号流图如下，试写出各自系统的输入输出方程。
信号与系统陈后金版答案
第二步:求差分方程的齐次 解： 2 求差分方程的齐次 第二步 h [ 0 ] = C 1 + C 2 r −5r /6 +1/ 6 = 0 1 k1 1 k 1 特征方程为: [ ( + 特征方程为=hCk1 ] = )[3 (C 2) ( −) 2 ( 求 ] u [ C ] = 3, C 2 = − 2 h [1] ⇒ ) 出 k1 ∴r =1/ 2, r2 =1/3 2 3 3 1 2
(3) 计算固有响应与强迫响应 计算固有响应与强迫响应:
1 7 1 k 4 1 k y[k ] = [ − ( ) + ( ) ]u[k ] 完全响应: 完全响应 2 2 2 3 3 7 1 k 4 1 k 固有响应: yh [k ] = [− ( ) + ( ) ]u[ k ] 固有响应 2 2 3 3 1 强迫响应: 强迫响应 y p [k ] = u[k ] 2 (4) 计算瞬态响应与稳态响应 计算瞬态响应与稳态响应:
特征根为 s1 = -2, s2 = -5, 又因为 n > m , 所以： 则 h ( t ) = K 1e − 2 t u ( t ) + K 2 e − 5 t u ( t )
h '(t ) = − 2 K 1e −2 t u (t ) + K 1δ (t ) − 5 K 2 e −5 t u (t ) + K 2δ (t ) = − 2 K 1e −2 t u (t ) − 5 K 2 e −5 t u (t ) + ( K 1 + K 2 )δ (t ) h ''(t ) = 4 K 1e −2 t u (t ) − 2 K 1δ (t ) + 25 K 2 e −5 t u (t ) − 5 K 2δ (t ) + ( K 1 + K 2 )δ '(t ) 代入方程有： = K 1 + K 2 = '( t ) = 2 K 2δ ( t ) + 5 K∴K2 + (7/3; K1 )δ −1/3; 2δ '( t ) + 3δ ( t ) 1δ ( t )
信号与系统课后答案(全)
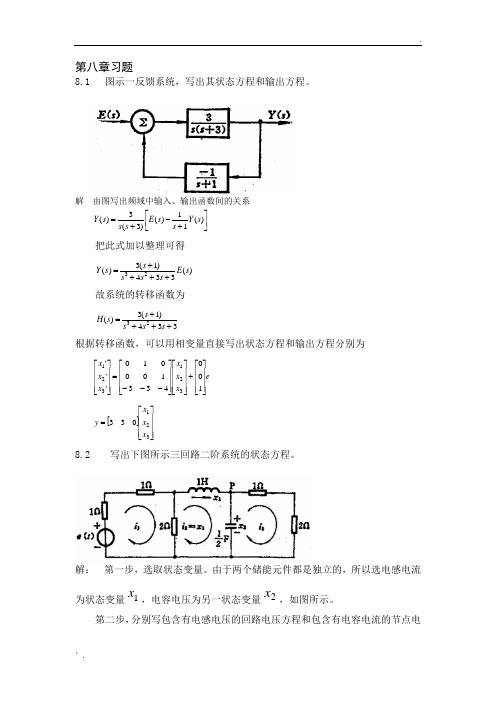
第八章习题8.1 图示一反馈系统，写出其状态方程和输出方程。
解由图写出频域中输入、输出函数间的关系⎥⎦⎤⎢⎣⎡+-+=)(11)()3(3)(sYssEsssY把此式加以整理可得)(334)1(3)(23sEsssssY++++=故系统的转移函数为334)1(3)(23++++=sssssH根据转移函数，可以用相变量直接写出状态方程和输出方程分别为exxxxxx⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡143311'''321321[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=32133xxxy8.2 写出下图所示三回路二阶系统的状态方程。
解：第一步，选取状态变量。
由于两个储能元件都是独立的，所以选电感电流为状态变量1x，电容电压为另一状态变量2x，如图所示。
第二步，分别写包含有电感电压的回路电压方程和包含有电容电流的节点电流方程。
根据第二个回路的回路方程，并代入元件参数，则有112122'ixxx+--=312'21ixx-=第三步，上两式中1i和3i不是状态变量，要把它们表为状态变量。
由第一个回路有1124xie-=，即112141xei+=由第三个回路有323ix=，即2331xi=把1i和3i分别代入第二步中两式，并经整理，最后得所求状态方程为exxx21'211+--=212322'xxx-=或记成矩阵形式8.3 图示一小信号谐振放大器的等效电路，这里的激励函数)(t e是一压控电流源，输出电压)(t y由耦合电路的电阻L R上取得。
要求写出此电路的状态方程和输出方程。
解：第一步，选状态变量。
因为电感电流和电容电压等三个变量都是独立的，所以选回路电感L中的电流1x、回路电容C上的电压2x、耦合电容c C上的电压3x为状态变量。
第二步，分别写回路方程或节点方程。
由RLC回路有211'xRxLx=+eixxCCx rc-=+++132''RL c i x C ='3第三步，消去非状态变量。
信号与系统第三版郑君里课后习题答案
信号与系统第三版郑君里课后习题答案第一章习题参考解1，判刑下列信号的类型解：()sin [()];y t A x t = 连续、模拟、周期、功率型信号 。
()()tt y t x ed τττ--∞=⎰连续、模拟、非周期、功率型信号。
()(2y n x n =） 离散、模拟、非周期、功率型信号。
()()y n n x n = 离散、模拟、非周期、功率型信号。
1－6，示意画出下列各信号的波形，并判断其类型。
(1) 0()s in ()x t A t ωθ=+ 连续、模拟、周期、功率型(2) ()t x t A e -= 连续、模拟、非周期、只是一个函数，不是物理量。
(3) ()c o s 0tx t ett -=≥ 连续、模拟、非周期、能量型 (4) ()2112,x t t t =+-≤≤ 连续、模拟、非周期、能量型(5) 4()(),0.5k x k k =≥ 离散、模拟、非周期、能量型(6) 0().j kx k eΩ= 离散、模拟、周期、功率型()s i n [()];()()()(2);()()tt y t A x t y t x ed y n x n y n n x n τττ--∞====⎰1－6题，1－4图。
t=-pi:1/200:pi;y1=1.5*sin(2*t+pi/6);subplot(4,1,1),plot(t,y1),title('1.5sin(2*t+pi/6)'),gridy2=2*exp(-t);subplot(4,1,2),plot(t,y2),title('2exp(-t)'),gridt1=0:1/200:2*pi;y3=10*exp(-t1).*cos(2*pi*t1);subplot(4,1,3),plot(t1,y3),title('10exp(-t1)cos(2*pi*t1)'),grid t2=-1:1/200:2;y4=2*t2+1;subplot(4,1,4),plot(t2,y4),title('2x+1'),grid习题1－6 5－6题n=0:pi/10:2*pi;y=(0.8).^n;subplot(4,1,1),stem(n,y,'fill'),title('(0.8)^n'),gridn1=0:pi/24:2*pi;y1=cos(2*pi*n1);y2=sin(2*pi*n1);subplot(4,1,2),stem3(y1,y2,n1,'fill'),title('exp[2*pi*n1'),gridsubplot(4,1,4),stem(n1,sin(2*pi*n1),'fill'),title('sin2pin1'),gridsubplot(4,1,3),stem(n1,cos(2*pi*n1),'fill'),title('cos2pin1)'),grid1－8，判断下列系统的类型。
《信号与系统(第2版》【附录+习题答案】
附 录 A 常 用 数 学 公 式A.1 三角函数公式j e cos jsin t t t ωωω=+ j e e (cos jsin )t t t σωσωω+=+j j 1cos (e e )2t t t ωωω-=+j j 1sin (e e )2jt t t ωωω-=-sin()sin cos cos sin αβαβαβ±=± cos()cos cos sin sin αβαβαβ±=sin22sin cos ααα=2222cos2cos sin 12sin 2cos 1ααααα=-=-=-1sin sin [cos()cos()]2αβαβαβ=--+1cos cos [cos()cos()]2αβαβαβ=-++1sin cos [sin()sin()]2αβαβαβ=-++双曲正弦：e e sh 2x xx --=双曲余弦：e e ch 2x xx -+=A.2 微积分公式d()d Cu C u =，C 为常数（下同）d()d d u v u v ±=±，u 、v 为t 的函数（下同） d()d d uv v u u v =+ 2d d d u v u u v v v -⎛⎫= ⎪⎝⎭d d Cu t C u t =⎰⎰()d d d u v t u t v t ±=±⎰⎰⎰信号与系统288d d u v uv v u =-⎰⎰()d ()()()()d ()bb baaau t v t u t v t v t u t =-⎰⎰A.3 数列求和公式（1）等比数列123,,,,N a a a a 的通项为11n n a a q -=，q 为公比，前n 项的和为 111(1)11NN N N n n a a q a q S a q q =--===--∑（2）等差数列123,,,,N a a a a 的通项为1(1)n a a n d =+-，d 为公差，前n 项的和为111()(1)22NN N n n N a a N N dS a Na =+-===+∑附 录 B 常 用 信 号 与 系 统 公 式B.1 连续时间信号的卷积121221()()()()d ()()d x t x t x x t x x t ττττττ∞∞-∞-∞*=-=-⎰⎰B.2 离散时间信号的卷积121221()()()()()()m m x n x n x m x n m x m x n m ∞∞=-∞=-∞*=-=-∑∑B.3 连续时间三角形式的傅里叶级数0000011()[cos()sin()]cos()kk kkk k x t a ak t b k t A A k t ωωωϕ∞∞===++=++∑∑0000001()d t T t a A x t t T +==⎰000002()cos()d 1,2,t T k t a x t k t t k T ω+==⎰， 000002()sin()d 1,2,t T k t b x t k t t k T ω+==⎰，1,2,k A k = arctan 1,2,k k k b k a ϕ⎛⎫=-=⎪⎝⎭，B.4 连续时间指数形式的傅里叶级数FS000j 01()e d t T k t k t X x t t T ω+-=⎰0j 0()()ek tk x t X k ωω∞=-∞=∑信号与系统290B.5 连续时间傅里叶变换FTj (j )()e d t X x t t ωω∞--∞=⎰j 1()(j )e d 2πt x t X ωωω∞-∞=⎰B.6 双边拉普拉斯变换()()e d st X s x t t ∞--∞=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰B.7 单边拉普拉斯变换0()()e d st X s x t t ∞--=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰，0t ≥B.8 离散时间傅里叶级数DFS2πj 1()()ekn NN N n N X k x n N -=<>=∑，0,1,2,k =±±2πj()()ekn NN N k N x n X k =<>=∑，0,1,2,n =±±B.9 离散时间傅里叶变换DTFTj j (e )()enn X x n ΩΩ∞-=-∞=∑j j 2π1()(e )e d 2πn x n X ΩΩΩ=⎰B.10 离散傅里叶变换DFT1()()01N knNn X k x n Wk N -==-∑≤≤，附 录 B 常 用 信 号 与 系 统 公 式29111()()01N kn Nk x n X k Wn N N--==-∑≤≤，B.11 双边Z 变换b ()()nn X z x n z∞-=-∞=∑11()()2n cx n X z z dzj π-=⎰B.12 单边Z 变换s 0()()nn X z x n z∞-==∑11()()2n cx n X z z dzj π-=⎰习题参考答案第1章1.1（a）确定信号、连续时间信号、非周期信号、能量信号、非因果信号。
信号与系统 人民邮电出版社 第二版第一章 课后答案
w
w
.k hd
第一章 信号与系统的基本概念 习题
南京邮电大学 信号分析与信息处理教学中心
aw
信号与系统
2006.1
.c
SIGNALS AND SYSTEMS
om
.c
∫
1 2 0
1-1 下列信号中哪些是周期信号，哪些是脉冲信号？哪 些是能量信号？哪些是功率信号它们的平均功率各为多 少？ ω 0t ω 0t j (ω 0t +θ )
om
∫
q
w
画系统 x (t ) q ∑ 模拟图：
∫
15
∑
y (t )
w
5
11
15
w
aw
) 1-23 已知某系统的数学模型为 y " ( t ) + a y ' ( t ) + a y ( t ) = b ' x ( t ) + b x ( t， 其模拟图如下，试导出微分方程中的系数 a1, a0 , b1, b0 与模拟图 与模拟 中的系数 α1,α0 , β1, β0的关系。 解：设辅助函数 q" x(t ) β0 β1 如图所示，则 q" = β 0 x + α 0 y + α1q' y (t ) q' q"
w
w
1 y ( t ) = {[[ x1( t ) + x2 ( t )]2 [[ x1( t ) x2 (t )]2 } 4 = x1(t ) x2 ( t )
.k hd
对所假设系统，有：
q(3) (t ) = x (t ) 5q" (t ) 11q' (t ) 15q(t )
信号与系统(吴大正)-完整版答案-纠错修改后版本
第一章 信号与系统1-1画出以下各信号的波形【式中)()(t t t r ε=】为斜升函数。
〔2〕∞<<-∞=-t et f t,)( 〔3〕)()sin()(t t t f επ=〔4〕)(sin )(t t f ε= 〔5〕)(sin )(t r t f = 〔7〕)(2)(k t f kε= 〔10〕)(])1(1[)(k k f kε-+=解：各信号波形为 〔2〕∞<<-∞=-t e t f t,)(〔3〕)()sin()(t t t f επ=〔4〕)=tfε)(sin(t〔5〕)rf=t(t)(sin〔7〕)f kεt=2()(k〔10〕)(])1(1[)(k k f k ε-+=1-2 画出以下各信号的波形[式中)()(t t t r ε=为斜升函数]。
〔1〕)2()1(3)1(2)(-+--+=t t t t f εεε 〔2〕)2()1(2)()(-+--=t r t r t r t f 〔5〕)2()2()(t t r t f -=ε 〔8〕)]5()([)(--=k k k k f εε 〔11〕)]7()()[6sin()(--=k k k k f εεπ〔12〕)]()3([2)(k k k f k ---=εε解：各信号波形为〔1〕)2()1(3)1(2)(-+--+=ttttfεεε〔2〕)2()1(2)()(-+--=t rt rt rtf〔5〕)2()2()(ttrtf-=ε〔8〕)]5()([)(--=k k k k f εε〔11〕)]7()()[6sin()(--=k k k k f εεπ〔12〕)]()3([2)(k k k f k ---=εε1-3 写出图1-3所示各波形的表达式。
写出图1-4所示各序列的闭合形式表达式。
1-41-5 判别以下各序列是否为周期性的。
如果是，确定其周期。
〔2〕) 63cos()443cos()(2ππππ+++=kkkf〔5〕)sin(2cos3)(5tttfπ+=解：1-6 信号)(tf的波形如图1-5所示，画出以下各函数的波形。
信号系统(第3版)习题解答
《信号与系统》（第3版）习题解析高等教育目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？(c) (d)题1-1图解 (a)、(c)、(d)为连续信号；(b)为离散信号；(d)为周期信号；其余为非周期信号；(a)、(b)、(c)为有始（因果）信号。
1-2 给定题1-2图示信号f ( t )，试画出下列信号的波形。
[提示：f ( 2t )表示将f ( t )波形压缩，f (2t)表示将f ( t )波形展宽。
](a) 2 f ( t - 2 ) (b) f ( 2t )(c) f ( 2t)(d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示，R 、L 、C 元件可以看成以电流为输入，电压为响应的简单线性系统S R 、S L 、S C ，试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i Lt u L L d )(d )(= ⎰∞-=tC C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。
S RS LS C题1-4图解 系统为反馈联接形式。
设加法器的输出为x ( t )，由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有)()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|，试判定该系统是否为线性时不变系统？解 设T 为系统的运算子，则可以表示为)()]([)(t f t f T t y ==不失一般性，设f ( t ) = f 1( t ) + f 2( t )，则)()()]([111t y t f t f T == )()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性，故为非线性时不变系统。
信号与系统课后答案
与奇分量的波形，相应如图题 1.12 中所示。
1-13 已知信号 f(t)的偶分量 fe(t)的波形如图题 1-13(a)所示， 信号 f(t+1)×U(-t-1)的波形如图题 1-13(b) 所示。求 f(t)的奇分量 fo(t)，并画出 fo(t)的波形。
解 因
f (t ) = f e (t ) + f 0 (t )
∫
t
−∞
δ (τ )dτ ，故根据现行系统的积分性有
y (t ) = ∫ h(τ (dτ = ∫ [δ (τ ) − δ (τ − 1) − δ (τ − 2) + δ (τ − 3)]dτ = u (t ) − u (t − 1) − u (t − 2) + u (t − 3)
1-2 已知各信号的波形如图题 1-2 所示，试写出它们各自的函数式。
解： f 1 (t ) = t[u (t ) − u (t − 1)] + u (t − 1)
f 2 (t ) = −(t − 1)[u (t ) − u(t − 1)]
f 3 (t ) = (t − 2)[u(t − 2) − u(t − 3)]
y 2 (t ) 的波形如图题 1.17(c)所示.
1-18 图题 1-18(a)所示为线性时不变系统，已知 h1(t)=δ(t)-δ(t-1), h2(t)=δ(t-2)-δ(t-3)。（1）求响 应 h(t)； （2） 求当 f(t)=U(t)时的响应 y(t)（见图题 1-18(b))。
解（1） h(t ) = h1 (t ) − h2 (t ) = δ (t ) − δ (t − 1) − δ (t − 2) + δ (t − 3) (2) 因 f (t ) = u (t ) =
信号与系统课后习题与解答第一章
1-1 分别判断图1-1所示各波形是连续时间信号还是离散时间信号，若是离散时间信号是否为数字信号？图1-1图1-2解 信号分类如下：⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--））（散（例见图数字：幅值、时间均离））（连续（例见图抽样：时间离散，幅值离散））（连续（例见图量化：幅值离散，时间））（续（例见图模拟：幅值、时间均连连续信号d 21c 21b 21a 21图1-1所示信号分别为 （a ）连续信号（模拟信号）； （b ）连续（量化）信号； （c ）离散信号，数字信号； （d ）离散信号；（e ）离散信号，数字信号； （f ）离散信号，数字信号。
1-2 分别判断下列各函数式属于何种信号？（重复1-1题所示问） （1）)sin(t e at ω-； （2）nT e -； （3）)cos(πn ；（4）为任意值）（00)sin(ωωn ；（5）221⎪⎭⎫⎝⎛。
解由1-1题的分析可知： （1）连续信号； （2）离散信号；（3）离散信号，数字信号； （4）离散信号； （5）离散信号。
1-3 分别求下列各周期信号的周期T ： （1）)30t (cos )10t (cos -； （2）j10t e ；（3）2)]8t (5sin [；（4）[]为整数）（n )T nT t (u )nT t (u )1(0n n ∑∞=-----。
解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号，需要考察各分量信号的周期是否存在公倍数，若存在，则该复合信号的周期极为此公倍数；若不存在，则该复合信号为非周期信号。
（1）对于分量cos (10t )其周期5T 1π=；对于分量cos (30t )，其周期15T 2π=。
由于5π为21T T 、的最小公倍数，所以此信号的周期5T π=。
（2）由欧拉公式)t (jsin )t (cos e t j ωωω+= 即)10t (jsin )10t (cos e j10t +=得周期5102T ππ==。
信号与系统课后答案（ＰＤＦ）
第二章第二章 课后题答案课后题答案2-1.1.图题2-1所示电路，求响应u 2(t)对激励f(t)的转移算子H(p)及微分方程。
解 其对应的算子电路模型如图题2.1（b ）所示，故对节点①，②可列出算子形式的KCL 方程为= +++−=−+0)(111)(1)()(1)(1312121t u p p t u p t f t u p t u p即()=+++−=−+0)(1)()()()(13122121t u p p t u t pf t u t u p联解得)()()(443)(22t f p H t f p p t u =++=故得转移算子为443)()()22++==p p t f t u p H （u 2(t)对f(t)的微分方程为()）（）（t f t u p p 34422=++即）（t f t u t u dt d t u dt d 3)(4)(4)(22222=++2-2图题2-2所示电路，求响应i(t)对激励f(t)的转移算子H(p)及微分方程。
解 其对应的算子电路模型如图2.2（b）所示。
故得）（）（t f p p p p pp t f t i 3011101022221.01)(2+++=+×++=故得转移算子为30111010)()()(2+++==p p p t f t i p Hi(t)对f(t)的微分方程为)()1010()()3011(2t f p t i p p +=++即)(10)(10)(30)(11)(22t f t f dt d t i t i dt d t i dt d +=++2-3图题2-3所示电路，已知u C (0-)=1 V, i(0-)=2 A。
求t>0时的零输入响应i(t)和u C (t)。
解 其对应的算子电路模型如图题2.3（b）所示。
故对节点N 可列写出算子形式的KCL 方程为0)(2312= ++t u p p C又有uc(t)=pi(t)，代入上式化简，即得电路的微分方程为=====++−+−+1)0()0(2)0()0(0)()23(2c cu u i i t i p p电路的特征方程为0232=++p p故得特征根（即电路的自然频率）为p 1=-1，p 2=-2。
信号与系统(郑君里)课后答案 第一章习题解答
1-4 分析过程：（1）例1-1的方法：()()()()23232f t f t f t f t →−→−→−− （2）方法二：()()()233323f t f t f t f t ⎡⎤⎛⎞→→−→−−⎜⎟⎢⎥⎝⎠⎣⎦（3）方法三：()()()()232f t f t f t f t →−→−+→−−⎡⎤⎣⎦ 解题过程：（1）方法一：方法二：（1）()−f at 左移0t ：()()()000−+=−−≠−⎡⎤⎣⎦f a t t f at at f t at （2）()f at 右移0t ：()()()000−=−≠−⎡⎤⎣⎦f a t t f at at f t at （3）()f at 左移0t a ：()()000⎡⎤⎛⎞+=+≠−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a （4）()f at 右移0t a ：()()000⎡⎤⎛⎞−−=−+=−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a 故（4）运算可以得到正确结果。
注：1-4、1-5题考察信号时域运算：1-4题说明采用不同的运算次序可以得到一致的结果；1-5题提醒所有的运算是针对自变量t 进行的。
如果先进行尺度变换或者反转变换，再进行移位变换，一定要注意移位量和移位的方向。
1-9 解题过程： （1）()()()2tf t eu t −=− （2）()()()232tt f t ee u t −−=+（3）()()()255ttf t e eu t −−=− （4）()()()()cos 1012tf t et u t u t π−=−−−⎡⎤⎣⎦1-12 解题过程：（（（（注：1-9、1-12题中的时域信号均为实因果信号，即()()()=f t f t u t 1-18 分析过程：任何信号均可分解为奇分量与偶分量之和的形式，即()()()()1e o f t f t f t =+其中，()e f t 为偶分量，()o f t 为奇分量，二者性质如下：()()()()()()23e e o o f t f t f t f t =−=−−()()13∼式联立得()()()12e f t f t f t =+−⎡⎤⎣⎦ ()()()12o f t f t f t =−−⎡⎤⎣⎦ 解题过程：(a-1) (a-2)(a-3)(a-4)f t为偶函数，故只有偶分量，为其本身(b) ()(c-1)(c-2)(c-3)(c-4)(d-1)(d-2)(d-3)(d-4)1-20 分析过程：本题为判断系统性质：线性、时不变性、因果性（1）线性（Linearity）：基本含义为叠加性和均匀性即输入()1x t ，()2x t 得到的输出分别为()1y t ，()2y t ，()()11T x t y t =⎡⎤⎣⎦，()()22T x t y t =⎡⎤⎣⎦，则()()()()11221122T c x t c x t c y t c y t +=+⎡⎤⎣⎦（1c ，2c 为常数）。
信号与系统(应自炉)习题答案第1章 习题解
第1章 习 题 解 答1-1．判断下列信号是否是周期性的，如果是周期性的，试确定其基波周期（1）()⎪⎭⎫⎝⎛+=43cos 2πt t f 解：对于()k Z ∈()222cos 32cos 322cos 333444f t k t k t k t f t ππππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+=++=++=+= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭∴原函数是周期函数，令1k =，则基波周期为23π。
（2）()26sin ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=πt t f解：对于()k Z ∈()()22sin sin 66f t k t k t f t ππππ⎡⎤⎡⎤⎛⎫⎛⎫+=+-=-= ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦∴原函数是周期函数，令1k =，则基波周期为π。
（3）()[]()t u t t f π2cos =解：设其存在周期，令周期为T()()()cos 2f t T t T u t T π+=++⎡⎤⎣⎦在0T ≠的情况下函数不为零的部分发生了平移，故()()f t T f t +≠∴原函数不是周期函数。
（4）())(42π+=t j et f解：对于()k Z ∈())()(())(()224442222j t k j t j t j k f t k eeeef t ππππππ+++++==⨯==∴原函数是周期函数，令1k =，则基波周期为2π。
1-2．求信号())14sin()110cos(2--+=t t t f 的基波周期。
解：cos(101)t +的基波周期为15π， s i n (41)t -的基波周期为12π二者的最小公倍数为π，故())14sin()110cos(2--+=t t t f 的基波周期为π。
1-3．设()3,0<=t t f , 对以下每个信号确定其值一定为零的t 值区间。
（1）()t f -1 （2）()()t f t f -+-21 （3）)()(t f t f --21 （4）()t f 3 （5）()3tf解：（1）()t f -1为()f t 反折后向右平移一个单位得到，故当()2t >-时()10f t -=（2）()2f t -为()f t 反折后向右平移两个单位得到，故当()1t >-时()20f t -=。
信号与系统课后答案(西南交大)
y x (t ) = 3e −2 t − 2 e−3 t t ≥ 0 y f ( t ) = te−2 t − e−2 t + e −3 t t ≥ 0
自由响应 2 e−2 t − e −3 t 强迫响应 te−2 t 稳态响应 0
暂态响应 te−2 t + 2e −2 t − e− 3t t ≥ 0
2.19 y f ( t ) =
2.22① t 3 u( t ) ④(
②∞
③( t−
1 2
1 1 −2 t + e )u( t ) 4 4
sin t + cost 1 −t − e )u( t ) ⑤ eu (t − 3) + e t − 2 u( 3 − t ) ⑥ cos(ωt + 45° ) 2 2 1 − cosπt cosπt − 1 1 1 2.23① u( t ) + u( t − 2) ② t 2 u( t ) − ( t − 1)2 u( t − 1) π π 2 2
3.6 f (t ) =
1 − j 3 ω0 t 3 − j 2 ω 0 t 3 1 e + e + e − jω 0 t + 1 + e jω 0 t + e j 2 ω0 t + e j 3 ω 0t 2 2 2 2
3.7 f (t ) = cos( 4ω0 t + 20°) + 2 cos( 2ω0 t + 30 °) + 3 cos(ω 0 t + 10° ) + 2
p2 + p +1 2.3 H ( p ) = 3 p + 2 p2 + 3p + 2 p2 + 3 p + 2 2.4 H ( p ) = 2p2 +3p +2
《信号与系统》习题参考答案
《信号与系统》习题参考答案（1）2—1（1） 01()()()()(1)()ta at x t h t x u t d e d e u t aτττττ∞---∞*=⋅-==-⎰⎰ （2） 00()()(cos sin )()x t h t t d ωτωτδττ∞-∞*=+⋅-⎰0000(cos sin )()cos sin t t t d t t ωωδττωω∞-∞=+⋅-=+⎰（3） 当0t <时 ()()0x t h t *=当01t ≤<时 20()()(1)2tt x t h t d t ττ*=+=+⎰当12t ≤<时 13()()(1)2x t h t d ττ*=+=⎰ 当23t ≤<时 12213()()(1)22t x t h t d t t ττ-*=+=-++⎰ 当3t ≥时 ()()0x t h t *= （4） 当0t <时 ()()0x t h t *=当0t ≥时 01()()sin 2(1cos 2)2tx t h t d t ττ*==-⎰ （5） 22222(2)2(4)241()()(2)2t t t t t t t x t h t e d e d e ee ττττ-----*=-=-+⎰⎰ （6）()x t at b =+11212()()()()()(2)3363tt x t h t a b d a tb t a t a bττδ-*=+++*--=++⎰2—2（1） [][][][2](2)[2]x n h n nu n n n u n δ*=*-=--（2） 10[][](2)[](21)[]nin i x n h n u n u n +=*==-∑（3） 当0n ≥时 1111[][]2()()232i n in i x n h n --=-∞*==∑ 当0n <时 111[][]2()223n i n i n i x n h n --=-∞*==⋅∑ （4） 当0n <时 [][]0x n h n *=当0n ≥时 110[][]()[]n n nin ii x n h n u n βααββα++-=-*==-∑（5） 当07n ≤≤时 071[][](1)[1(1)]2in i n x n h n -=-*=-=--∑ 当70n -≤≤时 71[][](1)[(1)1]2ni n i x n h n -=-*=-=--∑ 2—3（1） 12()()[(1)(1)][(5)(5)]x t x t u t u t t t δδ*=+--*++- (6)(4)(4)(6)u t u t u t u t =++--+-- （2） 123()()()x t x t x t **{[(6)(4)][(4)(6)]}*[u t u t u t u t =+-++---11()()]22t t δδ++- ( 6.5)( 4.5)( 5.5)( 3.5)( 3.5)( 5.5)u t u t u t u t u t u t =+-+++-++--- ( 4.5)( 6.5)u t u t +---（3） 1311()()[(1)(1)][()()]22x t x t u t u t t t δδ*=+--*++- ( 1.5)(0.5)(0.5)( 1.5)u t u t u t u t =+--++-- 2—4 0(3)331()(3)1t k k t tk k y t eu t k e e e e∞-----=-∞=-∞=-=⋅=-∑∑311A e-=- 2—5（1） 当2t ≥时 ()()0x t h t *= 当20t -<<时 11()()2t x t h t d t τ+-*==+⎰当02t <<时 11()()2t x t h t d t τ-*==-⎰（2） 当01t <<时 1()()22(1)tx t h t d t τ*==-⎰ 当10t -<<时 01()()22(1)2t tx t h t d d t t t ττ+*=+=-++=+⎰⎰当21t -<<-时 11()()2t x t h t d t τ+-*==+⎰当 1t ≥ 或 2t <-时 ()()0x t h t *=此题也可利用性质，先对()x t 积分，对()h t 微分，'()()()y t x t dt h t =*⎰（3） 当0t <时 (1)1()()1t x t h t e dt +∞--*==⎰当0t ≥时 1(1)(1)11()()22t t t t t x t h t e dt e dt e ++∞-----+*=+=-⎰⎰（4） 当t π< 或 5t π>时 ()()0x t h t *= 当3t ππ<<时 0()()sin 1cos t x t h t d t πττ-*==+⎰当35t ππ<<时 23()()sin 1cos t x t h t d t ππττ-*==--⎰（5） 当01t <<时 2211()()222()22x t h t t t t *=-=--当12t <≤时 2231()()264[2()]22x t h t t t t *=-+-=---()()x t h t *是以2为周期的周期函数 2—7（1） 111[][1]()[]()[1]22nn h n Ah n u n A u n ---=--111()[()()][1]()22nn n A u n n δδ-=+--=12A =（2） 111[][][][1][][]h n h n Ah n h n h n n δ---*-*-=*11[][][1]2h n n n δδ-∴=-- （3） 11[][][]2[[][1]][]nx n h n h n u n u n h n --**=--* 2[]2[[][4]]2[[1][5]]nn x n u n u n u n u n -∴=------2—8（1） 0()3()y t y t =（2） 00()()(2)y t y t y t =-- （3） 0()(1)y t y t =- （4） 0()()y t y t =-（5） 0()()dy t y t dt=（6） 202()()d y t y t dt =2—9 12111[][]()[]()[1]222n n x n h n u n u n -*=-+--1()([][1])[]2nu n u n n δ=---=1221[][][][]([][])*[]y n x n h n h n x n h n h n =**=* []*([][])[][]n n n n n u n u n u n u n δαβαβ=+=+ 2—10（1） 341201[][]((0.5))[3]2(1())[3]2n nn n x n x n u n u n ++=*=+=-+∑ （2） 4123[][][]2(1(0.5))[3]([][1])n x n x n x n u n n n δδ+**=-+*-- 43312(1(0.5))[3]2(1(0.5))[2]()[3]2n n n u n u n u n +++=-+--+=+ （3） 23[][][3]([][1])[3][2][3]x n x n u n n n u n u n n δδδ*=+*--=+-+=+ 2—11（1） 12345[][]([][][])[]h n h n h n h n h n h n =*-*+ （2） 34[][][1]h n h n nu n *=- 234[][][](1)[][1][]h n h n h nn u n n u n u n -*=+--= 12345[][]([][][])[]h n h n h n h n h n h n =*-*+514()([][3])*[][]2nu n u n u n hn =--+ 4[]6[1]7[2][]4[3]5[]6[1]7[2]4[3]n n u n n n n n u n n δδδδδδδ=+-+-++-=+-+---（1）'()()(2)(2)()(2)tt y t e x d x t y t x t τττ---∞=--+-=-+-⎰(2)()(2)t h t eu t --=- （2）当1t ≤时 ()0y t =当14t <≤时 1(2)(1)2()1t t y t e d e ττ+----==-⎰当4t >时 1(2)(4)(1)2()t t t t y t e d e e ττ+-------==-⎰2—13（1）213()()()()(1)[()](1)[()](1)h t h t h t u t t t u t t u t δδδ**=*-*-=-*-=-- 1213()()()()()()(1)h t h t h t h t h t u t u t =+**=--（2）1(10)1(02)()3(23)0t t t y t t t +-<<⎧⎪<<⎪=⎨-<<⎪⎪⎩其余2—14（1）因果、稳定 （2）非因果、非稳定 （3）非因果、稳定 （4）非因果、稳定 （5）非因果、稳定 （6）因果、稳定 （7）因果、非稳定 2—15（1）因果、稳定 （2）非因果、稳定 （3）非因果、非稳定 （4）非因果、稳定 （5）因果、非稳定 （6）非因果、稳定 （7）因果、稳定 2—16（1）对 （2）对()h t dt ∞-∞=+∞⎰（3）错 例如单位冲激响应(1)t δ-是因果的，但LTI 系统的逆系统(1)t δ+不是因果的。
《信号与系统》第二版课后答案_（郑君里）_高等教育出版社
5t −∞
e2
(τ
)
dτ
= c1r1 (t ) + c2r2 (t )
∫ ∫ ∫ ( ) ( ) ( ) ( ) ( ) 时变：输入 e t − t0
，输出
5t
e
−∞
τ
− t0
τ −t0 = x
dτ =
e 5t −t0
−∞
x
dx ≠
e 5(t−t0 )
−∞
x
dx = r
t − t0
非因果： t
= 1时，
解题过程： （1）方法一：
f (t)
1
f (t − 2)
1
→
-2
-1
f (3t − 2)
0
1
→
1
2
f (−3t − 2)
1
→
3
2/3 1
-1 -2/3
方法二：
f (t)
f (3t )
1
1
→
→
-2
-1
f (3t − 2)
0
1
-2/3
→
1/3
f (−3t − 2)
2/3 1 方法三：
-1 -2/3
1
f (t)
（2） r (t ) = e(t )u (t )
线性：设 r1 (t ) = e1 (t )u (t ) 、 r2 (t ) = e2 (t )u (t ) ， 则 ⎡⎣c1e1 (t ) + c2e2 (t )⎤⎦ u (t ) = c1r1 (t ) + c2r2 (t )
6
时变：输入 e (t − t0 ) ，输出 e (t − t0 )u (t ) ≠ e (t − t0 )u (t − t0 ) = r (t − t0 ) 因果： r (t ) 仅与此时刻 e (t ) 有关 （3） r (t ) = sin ⎡⎣e(t )⎤⎦ u (t ) 非线性：设 r1 (t ) = sin ⎡⎣e1 (t )⎤⎦ u (t ) 、 r2 (t ) = sin ⎡⎣e2 (t )⎤⎦ u (t ) ， 则 sin ⎡⎣c1e1 (t ) + c2e2 (t )⎤⎦ u (t ) ≠ sin ⎡⎣c1e1 (t )⎤⎦ u (t ) + sin ⎡⎣c2e2 (t )⎤⎦ u (t ) 时变：输入 e (t − t0 ) ，输出 sin ⎡⎣e (t − t0 )⎤⎦ u (t ) ≠ sin ⎡⎣e(t − t0 )⎤⎦ u (t − t0 ) = r (t − t0 ) 因果： r (t ) 仅与此时刻 e (t ) 有关 （4） r (t ) = e (1− t ) 线性：设 r1 (t ) = e1 (1− t ) 、 r2 (t ) = e2 (1− t ) ，则 c1e1 (1− t ) + c2e2 (1− t ) = c1r1 (t ) + c2r2 (t ) 时变：设 e1 (t ) = u (t ) − u (t −1.5) ，则 r1 (t ) = u (t + 0.5) − u (t ) e2 (t ) = e1 (t − 0.5) = u (t − 0.5) − u (t − 2) ，则 r2 (t ) = u (t +1) − u (t − 0.5) ≠ r1 (t − 0.5) 非因果：取 t = 0 ，则 r (0) = e (1) ，即 t = 0 时刻输出与 t = 1时刻输入有关。 （5） r (t ) = e(2t ) 线性：设 r1 (t ) = e1 (2t ) 、 r2 (t ) = e2 (2t ) ，则 c1e1 (2t ) + c2e2 (2t ) = c1r1 (t ) + c2r2 (t ) 时变：设 e1 (t ) = u (t ) − u (t − 2) ，则 r1 (t ) = u (t ) − u (t −1) e2 (t ) = e1 (t − 2) = u (t − 2) − u (t − 4) ，则 r2 (t ) = u (t −1) − u (t − 2) ≠ r1 (t − 2) 非因果：取 t = 1，则 r (1) = e (2) ，即 t = 1时刻输出与 t = 2 时刻输入有关。 （6） r (t ) = e2 (t ) 非线性：设 r1 (t ) = e12 (t ) 、 r2 (t ) = e22 (t ) ， 则 ⎡⎣c1e1 (t ) + c2e2 (t )⎤⎦2 = c12e12 (t ) + c22e22 (t ) + 2c1c2e1 (t ) e2 (t ) ≠ c1r1 (t ) + c2r2 (t ) 时不变：输入 e (t − t0 ) ，输出 e2 (t − t0 ) = r (t − t0 ) 因果： r (t ) 仅与此时刻 e (t ) 有关
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一章作业解答1.9解：（b ） jtt t j e e e t x −−+−==)1(2)(由于，故不是周期信号；)()(2)1()1())(1(2t x e e e T t x T j t j T t j ≠==++−+−++−（或者：由于该函数的包络随t 增长衰减的指数信号，故其不是周期信号；） （c ） 则n j e n x π73][=πω70=7220=ωπ是有理数，故其周期为N=2； 1.10解：10)110cos(21=→+ωt ，则：5211πωπ==T4)14(s 2=→−ωt in ，则：2422ππ==T 则：整个信号的周期为：π==},{21T T LCM T1.11解：74174nenjπωπ=→，则：k N 11277422===ππωπ，71=⇒N 52252nen jπωπ=→，则：kN 22255222===ππωπ，52=⇒N直流信号‘1’不影响信号的周期，故整个信号的周期为：35},{21==N N LCM N1.12解：]4[1][1)1(]1[1][43−−=−−==+−−−=∑∑∞=∞=n u m n mk k n n x m k δδÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿÿ 西南科技大学信号与系统教材课后习题参考答案（魏冬梅老师布置的作业）-3 –2 –1 0 1 2 3 4 5 6 n1…减去：-3 –2 –1 0 1 2 3 4 5 6 nu[n-4]等于：…-3 –2 –1 0 1 2 3 4 5 6 n故：即：M=-1，n ]3[+−n u 0=-3。
1.13解：)2()2()]2()2([)()(−−+=−−+==∫∫∞−∞−t u t u d d x t y ttττδτδττt则：41|)(|222∫∫−∞∞−∞===dt dt t y E 1.14解：x(t)的一个周期如图(a)所示，x(t)如图(b)所示：…而：g(t)如图(c)所示……dtt dx )(如图（d ）所示：…故：)1(3)(3)(−−=t g t g dtt dx 则：1t ,0t 3,32121==−==；A A 1.15解：该系统如下图所示： 2[n]（1）]4[2]3[5]2[2]}4[4]3[2{21]}3[4]2[2{]3[21]2[][][1111111222−+−+−=−+−+−+−=−+−==n x n x n x n x n x n x n x n x n x n y n y即：]4[2]3[5]2[2][−+−+−=n x n x n x n y（2）若系统级联顺序改变，该系统不会改变，因为该系统是线性时不变系统。
（也可以通过改变顺序求取输入、输出关系，与前面做对比）。
1.17解：（a ）因果性：)(sin )(t x t y =举一反例：当)0()y(,0int s x t =−=−=ππ则时输出与以后的输入有关，不是因果的；（b ）线性：按照线性的证明过程（这里略），该系统是线性的。
1.20解：（a ）)(21)2cos()(221t j tj e e t t x −+== 则：)(21)}(21{)(33221t j t j t j t j e e e e T t y −−+=+=；(b) t j j t j j t j t j e e e e e e t t x 2121)12()12(22121)(21))21(2cos()(−−−−−+=+=−=则：31(3cos )(212121)()31(3)31(331312−=+=+=−−−−−t e e e e e e t y t j t j t j j t j j（注意：此系统不是时不变系统。
） 1.21(a) x(t-1)(b)x(2-t)（c ）x(2t+1)(d)x(4-t/2)（e ）[x(t)+x(-t)]u(t)(f))]23-(t )23(tx(t)[δ−+δ1.22(a)x[n-4]1111x[n-4](b)x[3-n]1111x[n+3]1x[-n+3]11 1 (c) x[3n]1x[3n]-1/2(d) x[3n+1]1x[n+1](e) x[n]u[3-n]=x[n]11 1 1x[n]u[3-n](f) ]2[2]-x[n −δn]2−n(g)x[n]1-21x[n]21n）（+1 1x[n]1-1x[n]1n ）（+(g) ]1-n x[2）（1111.23则：)]()([21)(t x t x t x e −+=，)]()([21)(t x t x t x o −−=分别如下图所示：（注意：在对信号做奇偶分解时，尽量用图形的方式直观；而表达式烦琐，且容易出错）1.25解：(a)34cos(3)(π+=t t x 是周期信号， 40=ω 220ππω==T1.26解：（a ）)176sin(][+=n n x π 760πω=则：3720=ωπ为有理数，故该信号是周期的，其周期N=7； （b ）)81cos(][π−=n n x 810=ω 则：πωπ1620=为无理数，故该信号不是周期的；(d))]4cos()43[cos(21)]42cos()42[cos(21)4cos()2cos(][n n n n n n n n n x ππππππππ+=−++==)43cos(n π的周期，81=N )4cos(n π的周期82=N ，故整个信号的周期N=8。
1.27先证明几个基本的系统：时移系统、反折系统、尺度系统的线性、时不变、因果、稳定性； 一：时移系统：)()(1t t x t y −=(1) 线性：)()()()(122111t t x t y t t x t y −=−=)()()1()1()()()()()(2121133213t y t y t x t x t t x t y t x t x t x +=−+−=−=→+=：满足可加性)()()()()()(11114414t ky t t kx t t x t y t kx t x =−=−=→= ：满足齐次性；故：时移系统是线性系统； (2) 时不变性：)()(111t t x t y −=令：)()()()()(101122012t t t x t t x t y t t x t x −−=−=→−= 而：)()(01101t t t x t t y −−=−统。
故时移系统是时不变系)()(201t y t t y =−（3）因果性：由定义可知，当，则系统是因果的；否则为非因果系统； 01≥t （4）记忆性：由定义可知，时移系统是记忆系统；（5）稳定性：，则∞<|x(t)|∞<|)t -x(t |0（由于信号进行时移后，不影响幅度）故时移系统是稳定的；二、 反折系统： 线性、时变、非因果、记忆、稳定； 三 、尺度系统：线性、时变、非因果、记忆、稳定；(a))2()2()(t x t x t y −+−=解：由于该系统由时移与反折系统所组成，故性质由二者决定: 线性、时变、非因果、记忆、稳定；（b ）)(]3[cos )(t x t t y =线性(略)：是线性的时不变性：)(]3[cos )(1t x t t y =令：)(]3[cos )(]3[cos )()()(0122012t t x t t x t t y t t x t x −==→−= 而：)()](3[cos )(01001t t x t t t t y −−=− 故系统时变)()(201t y t t y ≠−(总结：若y(t)与x(t)之间的关系除了x(t)的形式外，还包括有关于t 的函数，则该系统是时变系统)因果性：输出仅与x(t)的当前值有关，故系统因果；(注意，因果性的定义：仅与当前值或以前值有关【二者只要满足一个就是】) 记忆性：输出仅与x(t)的当前值有关，故为非记忆系统；稳定性：由于cos3t 是有界的函数，则x(t)有界，y(t)有界，故系统稳定；（c ）∫∞−=td x t y 2)()(ττ解：线性：该系统是线性的（参考1小题证明）；时不变性：∫∞−=td x t y 211)()(ττ 令：)()(012t t x t x −=则：∫∫∫∫−∞−−∞−∞−∞−===−−==021210201222)(')'(')()()(t t t t tt d x d x t d t x d x t y ττττττττττ令而：∫∫−∞−−∞−==−00221)(2101)()()(t t t t d x d x t t y ττττ故系统时变)()(201t y t t y ≠−（注意，若这里的积分上限是t ，不是2t ，则系统是时不变的） 其他为：记忆、非因果，不稳定； （d ）该式改写为：)()]2()([)(t u t x t x t y −+=线性：系统是线性、时变、因果、记忆、稳定的； 所有答案如下表所示：记忆 时变 线性 因果稳定 a 是 是 是 非 是 b 非 是 是 是 是 c 是 是 是 非 非 d 是 是 是 是 是 e 是 否 否 是 是 f 是 是 是 非 是 g是否是非非1.31解：(a))2()((112−−=t x t x t x 由于该系统是LTI 系统，则)2()((112−−=t y t y t y（b ）)1()1((113−++=t x t x tx由于该系统是LTI 系统，则)1()1()(113−++=t y t y t ytt第二章作业解答2.1解：（a ）由多项式相乘法：3,2,1,0}1,0,2,1{][=−=n n x 1,0,1}2,0,2{][−==n n h1 2 0 -12 0 22 4 0 -22 40 -2 2 4 2 2 0 -2定义域为：[0-1：3+1]=[-1,4] 即：4,3,2,1,0,1}2,0,2,2,4,2{][−=−=n n y （b ）由性质：（若][][*][],[][*][00n n y n n h n x n y n h n x −=−=则：）得：][]2[][*]2[2n y n y n h n x =+=+ 则：2,1,0,1,2,32}2,0,2,2,4,2{][−−−=−=n n y（c ）同(b)：]2[]2[*][][3+=+=n y n h n x n y2.3解：x[k]、h[n-k]如图所示：0 1 2 3 4 5 kx[k]-1+n n 1+n 2+n k])21(1[2211)21()21(4)21()21()21(][0220][022*******22+++=−−+=−=−−===>>+=<<+∑∑n n kn k k n k n y n n n y n n 时，时，即：当时，时，即：当即：][]21(1[2][1n u n y n +−=2.5解：由题意：{}90:][n x {}N n h 0:][则：{}90:][+N n y 而：0]14[=y 则说明5<N又：⎪⎪⎪⎩⎪⎪⎪⎨⎧+>+≤≤−+<≤+<<+<==N n N n n N n N N N n 909999101n 0n 0h[n]*x[n]y[n]][n y 的最大值为N+1 结合：5]4[=y ，故N=4；2.7解：注意此题只是线性系统，非时不变系统。