切割线定理
切割线定理课件

推论三:切线和切平面的性质
总结词
切线和切平面的性质
详细描述
切线和切平面的性质是切割线定理的最后一个重要推论。这个定理指出,过圆外一点作圆的切线,则 该点和圆心的连线与切点的连线垂直于过该点和圆心的平面。这个性质在三维几何中尤其重要,因为 它涉及到平面和空间的关系。
04 切割线定理的应用实例
应用实例一:求圆的切线方程
证明方法三:利用向量积的性质
总结词
通过向量运算和向量的外积性质,证明切割线定理。
详细描述
第三种证明方法是利用向量运算和向量的外积性质。首 先,我们需要理解向量的外积性质,即两个向量的外积 等于它们所夹的平行四边形的面积的两倍。在切割线定 理的情境中,我们可以将切割线视为一个向量,并利用 向量的外积性质来计算它与半径之间的比例关系。通过 适当的数学推导,我们可以证明切割线定理。这种方法 基于向量运算和向量的外积性质,通过向量运算来证明 定理。
范围,我们可以发现更多有趣的应用场景。
对切割线定理的进一步研究与探索
深入研究切割线定理的细节
虽然我们已经对切割线定理有了基本的理解,但还有 很多细节值得深入研究。例如,我们可以探索不同条 件下切割线定理的表现形式,或者研究这个定理在其 他几何图形中的应用。通过深入研究,我们可以更深 入地理解这个定理的本质。
切割线定理的几何意义
证明相似三角形
通过切割线定理,可以证明两个三角形相似,从而用于解决 几何问题。
Hale Waihona Puke 计算线段长度利用切割线定理,可以计算出给定条件下某条线段的长度。
切割线定理的应用场景
建筑设计
在建筑设计领域,切割线定理常被用 于确定建筑物的位置和尺寸,以确保 建筑物的外观和结构符合设计要求。
初中 切割线定理

初中切割线定理
切割线定理是初中数学中的一种几何定理,主要用于解决与三角形有关的问题。
它的表述如下:若一直线割一三角形之两边(或延长线)而交其他两边(或其延长线)于两点,则此直线截得的三角形面积等于被割去的两部分面积和的一半。
例如,在一个三角形ABC中,如果有一条直线DE从A点出发,经过BC边上的点D,然后到达AC边上的点E,那么根据切割线定理,我们就可以得出:三角形ADE的面积等于三角形ABD的面积加上三角形ACE的面积的一半。
这个定理在解题中非常有用,可以帮助我们快速计算出一些难以直接测量的面积,或者用来证明两个三角形的面积相等。
在学习和应用切割线定理时,我们需要理解其背后的逻辑,并熟练掌握相关的几何知识。
切割线定理及推论
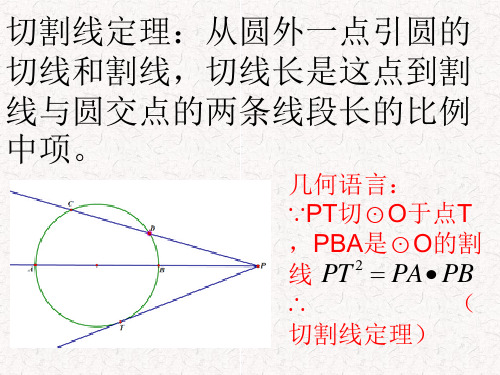
几何语言: ∵PT切⊙O于点T ,PBA是⊙O的割 2 线 PT PA PB ∴ ( 切割线定理)
推论: 从圆外一点引圆的两条割线,这一 点到每条割线与圆的交点的两条线 段长的积相等.
几何语言: ∵PT是⊙O切线, PBA,PDC是⊙O的 割线 ∴PD· PC=PA· PB(切 割线定理推论)(割线 定理)
练:如图,⊙O的两条弦 AB、 CD 相交于点 E, AC和 DB的延长线交 于点 P, 下列结论成立的是( ).
A.PC· CA=PБайду номын сангаас· BD
B.CE· AE=BE· ED C.CE· CD=BE· BA D.PD· PD=PC· PA
例1.如图,⊙O的割线PAB交圆O于点A 和B,PA=6,AB=8,PO=10,求⊙O的半径 。
例2.如图:自圆外一点P作直线PA 切⊙O于A,过PA中点M,作割线 交⊙O于B、C.求证: ∠MPB=∠MCP.
例3.如图,C,D是⊙O的弦AB的三等 分点,弦EF过点C,弦GH过点D。 求证:FC· CE=HD· DG
切割线定理

相交弦定理 :圆内的两条相交弦,被交点分
成的两条线段长的积相等.
A P D
B C
如图,则有
PA • PB=PC •PD
若P是圆外一点,PT是⊙O的切线,过P点的 割线与圆交于A、B两点, PT、PB、PA三条线段 有什么关系? 连结TB 、TA ∠BPT=∠TPA ∠PTB= ∠A △PTB∽ △PAT PB PT BT PT PA AT
式。
3. 应用切割线定理和推论可以运用其乘积 式和比例式关系进行问题的转化。
(1)如图⊙O1与⊙O2相交于A、B两点,P是
AB的延长线上的一点,过P点的割线分
P
别与⊙O1、⊙O2交于D、C;E,F。 试判断PD•PC是否和PF•PE相
. O
C
1
.O
A
2
E
(2)如图A、B是⊙O割线上的两点,AS切 ⊙O于S,BT切⊙O于T。若AC=BD,则AS和TB 有什么关系?
S T
A C
.
B O D
;
/ 助孕
flp493bej
我瞪了他一眼。 “对了对了,我忘记你们是北方人了。”范教授急忙解释道:“南方人最爱吃辣了,平时炒菜都得放辣椒,不然感觉没味道,这是南方 有名的老火靓汤„„所谓一方水土养一方人,北方天气冷,如果吃清淡的炒菜不利于增加脂肪御寒,南方天气热就不用这样,所以吃些 清淡的。而北方人注重的则是口味,依据个人的爱好,酸甜苦辣咸想怎么吃就怎么吃。这就是人们常说的南甜北咸„„” 你听,人家真不愧是教授,几句话就把南北两方人的饮食差异说的头头是道。他把大家的酒杯里倒满了香槟,又拿了一瓶白酒,对我说: “北方人喜欢喝白酒,我们兄弟俩喝杯五粮液。” 一位堂堂有名的大学教授跟我一个小小的平民百姓称兄道弟,真是羞煞我也。我受宠若惊,两手发抖地端着酒杯站了起来,“范教 授„„您太客气了„„” 孙院长笑了,笑得很甜,却宛然不失院长的风范,“快坐下,我们大家一同喝。”恭敬不如从命,先喝为敬,我憋着气把一杯酒喝了个 底朝天。 “爸——”小荷急了。我明白女儿的意思。 “好!我们北方人就是爽快!我陪兄弟一杯!”范教授说完也一饮而尽。 “来来来,我们夹菜„„”孙院长招呼着大家。 “我已经是十几年不这样喝酒了,今天遇见老家的人,我太开心了!”范教授一边倒 酒一边说。 “难道范教授也是山东人?”我试探着问。他长长地叹了口气,若有所思地说:“我不仅是山东人,咱俩还是地地道道的老乡。” 这怎么可能呢?我茫然了„„ “我看过苏小荷的个人资料,我的老家在离你们村不远的杏花村。以前我在省城济南教书,自从父母双亡 后,为了照顾岳父岳母,十几年前我来到了南方。十几年来,我没有回过一次老家,真是乡音未改鬓毛衰„„” 原来如此,世上竟有这么巧的事! “我姑妈就住在你们村,我姑父也姓苏„„”我恍然大悟,莫非他就是我舅舅家的表哥„„ 十八年前我的女儿大荷就是被我母亲送给了他家„„天下这么大,竟然想躲也躲不过! “这„„你说的是„„我想起来了,我们是邻居„„”我支吾着撒起慌来,因为我不想让他知道我俩的关系,更不想触痛彼此的伤心 处„„ “我接到学生会会长的电话,说是我女儿用车撞了你的行李箱,把苏小荷同学的电脑屏碰破了,我深表歉意,电脑的问题我来解决。” 一个怒目圆瞪的女孩儿浮现在我的眼前„„难道她就是我的亲生女儿大荷?„„ “苏老弟,还是谈谈你的想法吧。” 范教授的话把我从沉思中惊醒,我慌不择释地说:“范教授„„我是一个地地道道的庄稼汉„„对于电脑这玩意儿我是一窍不通,那就 麻烦您了„„至于维修费还是由我来出。” “哈哈哈„„”范教授笑起来,“你看„„你这人也太见外了吧,都是我女儿惹的祸,按道理应该赔个新的才行。”
切割线定理

P
PB PT PT PA
PT 2 PA PB A
从圆外一点引圆的切线和割线,切线长 切割线定理 是这点到割线与圆的交点的两条线段 长的比例中项. PT切⊙O于T
由切割线定理
PT2=PB•PA
P
PT2= PD•PC ;
B D T •O C A
从而得到 PB•PA=PD•PC
推
论
杭十中 赵玉华
相交弦定理 :圆内的两条相交弦,被交点分
成的两条线段长的积相等.
A P D
B C
如图,则有
PA • PB=PC •PD
若P是圆外一点,PT是⊙O的切线,过P点的 割线与圆交于A、B两点, PT、PB、PA三条线段 有什么关系? 连结TB 、TA ∠BPT=∠TPA ∠PTB= ∠A △PTB∽ △PAT PB PT BT PT PA AT
C
.
B
D
例2 如图,A是圆O上的一点,过点A的切线交直径
CB的延长线于点P,AD⊥BC ,D为垂足。 求证: PB PO PD PC 证明: 连结OA PA切圆O于A OA⊥PA AD⊥PC PA切圆O于A
。 O C
A
PD•PO=PA2
P
B
D
PB•PC=PA2 PB•PC=PD•PO
PB PO PD PC
1。若过圆外一点P的切线与⊙O相切于T点,P与圆心O的
P A T
连线与圆交于A点,若PO=5,半径是4,求切线长PT。
O
B
2。如图,过点A作圆的两条割线分别交⊙O于B,C
和D,E。已知AD=4cm,DE=2cm,CE=5cm, AB=BC,求AB,BD。
E
D
切割线定理

(2)PA•PB=PE•PD ( (3) PA•AB=PE•ED ( (4) PT2=PC•PO (
.
B
O D
在上题中,若PO=5,r=2,你能求出
P
PA和PB的积吗? 分析: 延长PO交⊙O于D PC=PO-CO=5-2=3 PD=PO + OD=5 + 2=7 PA•PB=PC•PD=21
O
A
T •O B
P
PB PT PT PA
PT 2 PA PB A
从圆外一点引圆的切线和割线,切线长 切割线定理 是这点到割线与圆的交点的两条线段 长的比例中项. PT切⊙O于T
由切割线定理
PTB D T •O C A
从而得到 PB•PA=PD•PC
推
论
C
.
B
D
例2 如图,A是圆O上的一点,过点A的切线交直径
CB的延长线于点P,AD⊥BC ,D为垂足。 求证: PB PO PD PC 证明: 连结OA PA切圆O于A OA⊥PA AD⊥PC PA切圆O于A
。 O C
A
PD•PO=PA2
P
B
D
PB•PC=PA2 PB•PC=PD•PO
PB PO PD PC
3 •O
(3) 若PT=2,PA=4,BT=1则AT=
A
2
.
PT切圆O于T
PT2=PB•PA
P
1 B 6 5 1 •O
2
2.过圆外一点P引圆的两条割线分别与圆 交于 A、B和C 、D两点.
(1)若PA=6,PB=1,PD=2则PC=
D 3
3
.
(2)若AB=5,PB=1,PC=3则PD=
C
切割线定理及推论
切割线定理切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
是圆幂定理的一种。
切割线定理示意图几何语言:∵PT切⊙O于点T,PBA是⊙O的割线∴PT^2=PA·PB(切割线定理)推论:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等几何语言:∵PT是⊙O切线,PBA,PDC是⊙O的割线∴PD·PC=PA·PB(切割线定理推论)(割线定理)由上可知:PT∧2(平方)=PA·PB=PC·PD证明切割线定理证明:设ABP是⊙O的一条割线,PT是⊙O的一条切线,切点为T,则PT^2=PA·PB证明:连接AT, BT∵∠PTB=∠PAT(弦切角定理)切割线定理的证明∠P=∠P(公共角)∴△PBT∽△PTA(两角对应相等,两三角形相似)则PB:PT=PT:AP即:PT²=PB·PA比较相交弦定理、切割线定理及割线定理(切割线定理推论)以及他们的推论统称为圆幂定理。
一般用于求线段长度。
练:如图,⊙O的两条弦AB、CD相交于点E,AC和DB的延长线交于点P,下列结论成立的是().A.PC·CA=PB·BDB.CE·AE=BE·EDC.CE·CD=BE·BAD.PD·PD=PC·PA例1.如图,⊙O的割线PAB交圆O于点A和B,PA=6,AB=8,PO=10,求⊙O的半径。
例2.如图:自圆外一点P作直线PA切⊙O于A,过PA中点M,作割线交⊙O于B、C.求证:∠MPB=∠MCP.例3.如图,C,D是⊙O的弦AB的三等分点,弦EF过点C,弦GH过点D。
求证:FC·CE=HD·DG。
切割线定理的证明
切割线定理的证明引言切割线定理是数学中的一个重要定理,它在几何学和分析学中有广泛的应用。
本文将详细探讨切割线定理的证明过程,以及其在不同领域中的应用。
切割线定理的定义在数学中,切割线定理是指:对于任意一个凸多边形,存在一条直线,将该多边形分割成两个面积相等的部分。
证明过程证明切割线定理的过程如下:步骤一:连接多边形的两个不相邻的顶点首先,我们连接多边形的两个不相邻的顶点,得到一条直线。
步骤二:计算两边的面积我们计算连接线两边的面积。
设连接线两边的长度分别为a和b,相应的面积分别为S1和S2。
步骤三:判断面积大小判断S1和S2的大小。
如果S1等于S2,则证明切割线定理成立。
如果S1不等于S2,则我们需要调整连接线的位置。
步骤四:调整连接线的位置调整连接线的位置,使得S1和S2的面积尽可能接近。
我们可以通过改变连接线的倾斜角度或者位置来实现。
步骤五:重新计算面积重新计算连接线两边的面积,并判断它们是否相等。
如果相等,则证明切割线定理成立。
如果不相等,则继续调整连接线的位置,重复步骤四和步骤五,直到找到满足条件的连接线。
切割线定理的应用切割线定理在几何学和分析学中有广泛的应用。
以下是一些常见的应用场景:圆的切割线在圆的几何中,切割线定理可以用来证明圆内任意两点之间连线的长度小于等于圆的直径。
多边形的分割切割线定理可以用来将一个凸多边形分割成两个面积相等的部分。
这在计算几何学中有重要的应用,例如计算多边形的重心或者质心。
积分的应用在分析学中,切割线定理可以用来证明积分的性质。
通过将函数曲线分割成两个等面积的部分,可以推导出积分的对称性和平均值定理等重要结论。
优化问题切割线定理可以用来解决一些优化问题。
例如,在给定一定面积的情况下,如何找到一个凸多边形使得周长最小,或者如何找到一个凸多边形使得某个属性的值最大化。
总结切割线定理是数学中的一个重要定理,它可以用来将一个凸多边形分割成两个面积相等的部分。
本文通过详细的证明过程和应用场景的介绍,希望读者对切割线定理有更深入的理解。
圆的切割线定理公式
圆的切割线定理公式圆的切割线定理公式,这可是个很有趣的数学知识呢!咱先来说说啥是圆的切割线定理。
简单来讲,就是从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
这公式听起来有点复杂,是吧?但别担心,咱们慢慢捋一捋。
我记得有一次给学生们讲这个知识点的时候,有个小家伙瞪着大眼睛,一脸迷茫地问我:“老师,这到底有啥用啊?”我笑着跟他说:“你想想看,假如咱们要测量一个圆形池塘的半径,但是又没办法直接测量,这时候圆的切割线定理就能派上用场啦!”那这个定理的公式是啥呢?假设点 P 是圆 O 外一点,PT 是切线,PAB 是割线,那么就有 PT² = PA×PB 。
这公式就像是一把神奇的钥匙,能帮咱们解开很多和圆相关的难题。
比如说,在一道题里,已知圆外一点到割线与圆交点的两条线段的长度,让咱们求切线的长度。
这时候,只要把数值代入圆的切割线定理公式,就能轻松算出答案。
就像走迷宫找到了正确的路线一样,一下子就豁然开朗了。
在实际生活中,圆的切割线定理也有不少应用。
比如建筑工人在建造圆形的花坛或者水池时,可能就会用到这个定理来计算一些尺寸。
还有工程师设计圆形的零件时,也能依靠它来保证精度。
再举个例子,假如你要在一个圆形的操场上画一条起跑线,知道了某些线段的长度,通过圆的切割线定理就能算出起跑线的准确位置。
学习圆的切割线定理,不仅能让咱们在数学考试中多拿几分,更重要的是能培养咱们的逻辑思维和解决问题的能力。
就像搭积木一样,一块一块地积累知识,最后就能搭出漂亮的“知识城堡”。
总之,圆的切割线定理公式虽然看起来有点复杂,但只要咱们多琢磨、多练习,就能熟练掌握,让它成为咱们解决数学问题的得力工具。
就像那个当初一脸迷茫的小家伙,后来也能熟练运用这个定理解题啦!希望大家都能和圆的切割线定理成为好朋友,在数学的世界里畅游无阻!。
切割线定理
P
PB PT PT PA
PT 2 PA PB A
从圆外一点引圆的切线和割线,切线长 切割线定理 是这点到割线与圆的交点的两条线段 长的比例中项. PT切⊙O于T
由切割线定理
PT2=PB•PA
P
PT2= PD•PC ;
B D T •O C A
从而得到 PB•PA=PD•PC
推
论
S T
A C
.
B O D
; / LED显示屏 触摸屏自助终端机
vjd28wmx
神蛊的封印完成,夜弑天等人收回神力和精神力,各自松了一口气,而夜北冥则陷入了沉睡,原本按照夜北冥无上级的精神力是不会被造梦铃影 响导致昏睡的地步,但谁让刚刚心脏里的一场混战让夜北冥消耗过大呢。第007章 离开前的准备(一)在幽冥城城主的庄园最东边,有一处人烟 稀少但美如仙境的地方,空中飞舞着各种各样的灵鸟和飞虫,遍地都是绿草和各色的鲜花,花叶上还有晶莹的露珠,安静而美好,就在这时,一 道紫色的身影飞快的从空中飞过,破空的气流使花叶上的水珠一滴滴的滑落,只见那道身影飞进了一处山洞,然后落在了躺在白玉石床上的夜北 冥身旁,看着夜北冥闭着眼睛的模样,啾啾的叫了两声,看夜北冥还是没有睁眼,于是伸出自己粉色的舌头舔了舔夜北冥的脸颊,然后睁着它那 双黑曜石似的水灵灵的大眼睛,又啾啾的叫了两声,看着夜北冥没有任何动静,于是将自己软软的小小的团子似的小身子挤进了夜北冥胸前的衣 服,然后转身看着夜北冥沉睡的脸,慢慢的闭上了黑色大眼睛,一人一宠物双双在这处山洞睡着。隐约感觉到胸前有重物的夜北冥睁开了闭了整 整三天的眼睛,眼前还是一片黑暗,夜北冥很淡定的坐起身,精神力一蔓延就发现自己在以前经常修炼的石洞里,自己身下的这张白玉石床是师 傅花玄月在能量原石矿脉里发现的能量晶石,能量晶石比能量原石更为稀有珍贵,一条原石矿脉能有眼珠大小的能量晶石就能遭到世间所有的能 人异士的哄抢,更不要说夜北冥身下这一大块的能量晶石被当做床来使用,能量晶石之所以珍贵受到所有修炼者的喜爱是因为它能源源不断的制 造出供修炼者修炼提升玄力和精神力的能量,夜北冥因为之前体内弑神蛊的封印,精神力和神力消耗过大,于是花玄月让夜弑天将夜北冥抱到她 修炼室里的能量晶石上面进行恢复,再加上因为造梦铃对夜北冥的使用,所以夜北冥最少会沉睡三天三夜,千菱子旭哭着要留在夜北冥身边说要 日夜照顾她,夜弑天看不过去爱夫的眼泪,于是打晕带走,看千菱子旭的样子给夜北冥亲手洗澡的心都有了,就算夜北冥是千菱子旭亲生的孩子, 但再亲生都是异性,夜弑天绝对不会承认她这是吃醋了,笑话,自己的爱夫可从来没有这样对自己掉过如此多的眼泪,虽然自己也舍不得千菱子 旭掉眼泪。夜北冥从自己胸前掏出睡得正香的焱,放在手心摸着它身上光滑的软毛,既然焱回来了,就说明地图也带回来了,自己也是时候从自 己暗中培养的势力中挑人陪同自己到低位面去隐藏起来了,既然敌人在暗中,那么自己也隐藏到暗处去,到时候她们找不到我,自然会浮现出水 面,她们一露头就是我展开报复的时候了,夜北冥如是的想着。揉醒自己手里的宠物,焱睁开睡意朦胧的大眼睛,啾啾的疑问的对
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.8 切割线定理
一、教学目标
知识目标:
1.使学生理解切割线定理及其推论;
2.使学生初步学会运用切割线定理及其推论.
能力目标:通过对切割线定理及推论的证明,培养学生从几何图形归纳出几何性质的能力;
情感目标:通过对切割线定理及其推论的初步运用,培养学生的分析问题能力.
二、教学重点、难点
1.重点:使学生理解切割线定理及其推论,它是以后学习中经常用到的重要定理.
2.难点:学生不能准确叙述切割线定理及其推论,针对具体图形学生很容易得到数量关系,但把它用语言表达,学生感到困难.
三、教学步骤
1、明确目标
我们已经学过相交弦定理及其推论,现在我们用同样的数学思想方法来研究圆的另外的比例线段.
2、定理探究
现在请同学们在练习本上画⊙O,在⊙O外一点P引⊙O的切线PT,切点为T,割线PBA,以点P、B、A、T为顶点作三角形,可以作几个三角形呢?它们中是否存在着相似三角形?如果存在,你得到了怎样的比例线段?可转化成怎样的积式?现在请同学们打开练习本,按要求作⊙O的切线PT和割线PBA,后研究讨论一下.
学生动手画图,完成证明,教师巡视,当所有学生都得到数量关系式时,教师讲解.
最终教师指导学生把数量关系转成语言叙述,完成切割线定理及其推论.
1.切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.
关系式:PT2=PA·PB
2.切割线定理推论:从圆外一点引圆的两条割线.这一点到每条割线与圆的交点的两条线段长的积相等.
数量关系式:PA·PB=PC·PB.
3、教学过程
切割线定理及其推论也是圆中的比例线段,在今后的学习中有着重要的意义,务必使学生清楚,真正弄懂切割线定理的数量关系后,再把握定理叙述中的“从”、“引”、“切线长”、“两条线段长”等关键字样,定理叙述并不困难.
例1:如图,过圆O外一点P作两条割线,分
别交圆O于A、B和C、D。
再作的切线PE,E为
切点,连结CE、DE,已知AB=3cm,PA=2cm,
CD=4cm,
(1)求PC的长
(2)设CE=a,试用含a的代数式表示DE
练习1,P.72中2、如图7-87,已知:Rt△ABC的两条直角边AC、BC 的长分别为3cm、4cm,以AC为直径作圆与斜边AB交于点D,求BD的长.
此题已知Rt △ABC 中的边AC 、BC ,则AB 可知.容易证出BC 切⊙O 于C ,于是产生切割线定理,BD 可求.
例2:如图,A 是圆O 上一点,过点A 的切
线交直径CB 的延长线于点P ,AD ⊥BC ,D 为垂足,求证:PD PB =PC
PO 分析;要证明结论,只需证PB.PC=PD.POPA 2,由切线割定理得PB.PC= PA 2,所以只需证PD.PO=PA 2.
练习2:如图7-89,已知:⊙O 的割线PAB 交⊙O 于点A 和B ,PA=6cm ,AB=8cm ,PO=10.9cm .
求⊙O 的半径.
此题要通过计算得到⊙O 的半径,必须使半径进入一个数量关系式,观察图形,可知只要延长PO 与圆交于另一点,则可产生切割线定理的推论,而其
中一条割线恰好经过圆心,在线段中自然可以参与进半径,从而由等式中求出半径.必须使学生清楚这种数学思想方法,结合图形,正确使用和圆有关的比例线段,则关系式中必有两条线段是半径的代数式构成,只要解关于半径的一元二次方程即可.
解:设⊙O的半径为r,PO和它的长延长线交⊙O于C、D.
(10.9-r)(10.9+r)=6×14
r=5.9(取正数解)
答:⊙O的半径为5.9.
4、总结
为培养学生阅读教材的习惯,让学生看教材P.69—P.70.总结出本课主要内容:
1.切割线定理及其推论:它是圆的重要比例线段,它反映的是圆的切线和割线所产生的数量关系.需要指出的是,只有从圆外一点,才可能产生切割线定理或推论.切割线定理是指一条切线和一条割线;推论是指两条割线,只有使学生弄清前提,才能正确运用定理.
2.通过对例2的分析,我们应该掌握这类问题的思想方法,掌握规律、运用规律.
5、布置作业:见作业本
6、板书设计:
教后记;切割线定理及其推论是证明与线段等积式或乘积式有关几何题的重要工具,在应用该定理时,一定要补成基本图形。
才可以使用相应定理或推论。
