柱坐标系偏导
导热微分方程柱坐标系的推导

导热微分方程柱坐标系的推导引言导热微分方程是描述物质内部热传导过程的重要方程。
在研究导热现象时,我们常常需要在不同的坐标系下推导导热微分方程。
本文将详细介绍如何在柱坐标系下推导导热微分方程,并给出相应的推导过程。
导热微分方程的一般形式在三维空间中,导热微分方程的一般形式可以表示为:∂u/∂t = α(∂^2u/∂x^2 + ∂^2u/∂y^2 + ∂^2u/∂z^2)其中,u表示温度场的变化,t表示时间,x、y和z分别表示空间的三个坐标轴方向。
α为热扩散系数,与物质的热导率有关。
柱坐标系下的导热微分方程柱坐标系是一种常用的坐标系,特点是以距离r、角度θ和高度z作为坐标轴。
在柱坐标系下,可以将导热微分方程表示为:∂u/∂t = α(1/r * ∂/∂r(r∂u/∂r) + 1/r^2 * ∂^2u/∂θ^2 + ∂^2u/∂z^2)其中,r表示距离,θ表示角度,z表示高度,u仍表示温度场的变化,t为时间,α为热扩散系数。
推导过程为了推导柱坐标系下的导热微分方程,我们需要使用二阶导数的链式法则和柱坐标系下的坐标变换关系。
首先,我们分别对r、θ和z求偏导:∂u/∂r = (∂u/∂x) * (∂x/∂r) + (∂u/∂y) * (∂y/∂r) + (∂u/∂z) * (∂z/∂r)∂u/∂θ = (∂u/∂x) * (∂x/∂θ) + (∂u/∂y) * (∂y/∂θ) + (∂u/∂z) * (∂z/∂θ)∂u/∂z = (∂u/∂x) * (∂x/∂z) + (∂u/∂y) * (∂y/∂z) + (∂u/∂z) * (∂z/∂z)根据柱坐标系的坐标变换关系:x = r * cos(θ)y = r * sin(θ)z = z可以得到:∂x/∂r = cos(θ)∂y/∂r = sin(θ)∂z/∂r = 0∂x/∂θ = -r * sin(θ)∂y/∂θ = r * cos(θ)∂z/∂θ = 0∂x/∂z = 0∂y/∂z = 0∂z/∂z = 1代入前面的式子,可以得到:∂u/∂r = (∂u/∂x) * cos(θ) + (∂u/∂y) * sin(θ)∂u/∂θ = -r * sin(θ) * (∂u/∂x) + r * cos(θ) * (∂u/∂y)∂u/∂z = (∂u/∂z)然后,我们可以对这些偏导数再次求偏导:∂^2u/∂r^2 = (∂/∂r(∂u/∂r)) = (∂/∂r((∂u/∂x) * cos(θ) + (∂u/∂y) * sin (θ)))∂^2u/∂θ^2 = (∂/∂θ(∂u/∂θ)) = (∂/∂θ(-r * sin(θ) * (∂u/∂x) + r * cos(θ) * (∂u/∂y)))∂^2u/∂z^2 = (∂/∂z(∂u/∂z))最后,将这些结果代入柱坐标系下的导热微分方程的一般形式中,即可得到柱坐标系下的导热微分方程:∂u/∂t = α(1/r * (∂/∂r(r * ((∂u/∂x) * cos(θ) + (∂u/∂y) * sin(θ)))) + 1/r^2 * (∂/∂θ(-r * sin(θ) * (∂u/∂x) + r * cos(θ) * (∂u/∂y))) + (∂^2u/∂z ^2))总结导热微分方程是描述物质内部热传导过程的重要方程。
梯度柱坐标表达式推导公式

梯度柱坐标表达式推导公式梯度是向量场中最重要的概念之一,用来描述标量函数在空间中变化的方向及强度。
梯度柱坐标表达式是一种表示梯度的方便方法,能够简化计算和分析标量函数在柱坐标系中的变化。
在本文中,我们将推导出梯度柱坐标表达式的具体公式。
柱坐标系简介柱坐标系是一种常用的坐标系,常用于描述在三维空间中具有柱对称性的问题。
柱坐标系由径向距离 r、方位角φ 和轴向距离 z 三个坐标表示。
其中,方位角φ 表示点在 xy 平面上的角度,径向距离 r 表示点到 z 轴的距离,轴向距离 z 表示点在 z 轴上的位置。
梯度的定义在直角坐标系中,标量函数 f(x, y, z) 的梯度表示为一个矢量,该矢量指向函数 f 在某一点上变化最快的方向,其模值表示变化的速率。
梯度的定义可以表示为:∇f = (∂f/∂x, ∂f/∂y, ∂f/∂z)其中,∇表示梯度算子,∂ 表示偏导数。
推导梯度的柱坐标表达式为了推导出梯度的柱坐标表达式,首先需要计算标量函数在柱坐标系下的偏导数。
柱坐标系中,一个点的坐标表示为P(r, φ, z)。
首先,我们来计算 r 方向上的偏导数∂f/∂r,为了在柱坐标系中计算偏导数,我们需要使用链式法则。
在直角坐标系中,r 可以通过以下关系来表示:x = r * cos(φ) y = r * sin(φ) z =z而 f(x, y, z) 则可以表示为在直角坐标系中的函数f(r * cos(φ), r * sin(φ), z)。
由链式法则可知:∂f/∂r = (∂f/∂x)(∂x/∂r) + (∂f/∂y)(∂y/∂r) + (∂f/∂z)(∂z/∂r)其中:∂x/∂r = cos(φ) ∂y/∂r = sin(φ) ∂z/∂r = 0对应地,上式可化简为:∂f/∂r = cos(φ)(∂f/∂x) + sin(φ)(∂f/∂y)同理,我们可以计算φ 方向上的偏导数∂f/∂φ 和 z 方向上的偏导数∂f/∂z,其结果如下:∂f/∂φ = (-sin(φ))(∂f/∂x) + cos(φ)(∂f/∂y) ∂f/∂z = (∂f/∂z)根据以上推导,我们得到了梯度柱坐标表达式的具体公式:∇f = ( ∂f/∂r, (1/r)(∂f/∂φ), ∂f/∂z )总结本文推导了梯度柱坐标表达式的具体公式。
圆柱,圆球坐标系
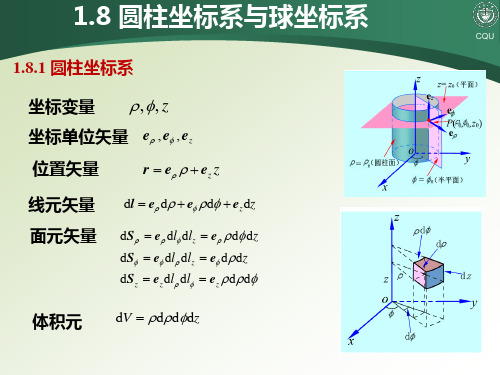
1.8 圆柱坐标系与球坐标系
CQU
三单位矢量e 有以下特点: 三单位矢量 ρ、eφ和ez有以下特点
三个单位矢量相互正交,且满足右手关系, 三个单位矢量相互正交,且满足右手关系,即 er× eθ= eφ; eθ× eφ = er ; eφ × er = eθ
球坐标系中的三度表达式
∇ = er ∂ 1 ∂ 1 ∂ + eθ + eφ ∂r r ∂θ rsinθ ∂φ
∇⋅F =
1 ∂ 2 1 ∂ 1 ∂Fφ (r Fr ) + (sinθ Fθ ) + r 2 ∂r rsinθ ∂θ r sinθ ∂φ
1 er 1 eθ rsinθ ∂ ∂θ rFθ 1 eφ r ∂ ∂φ rsinθ Fφ (r ≠ 0)
(r ≠ 0)
r 2sinθ ∂ ∇× F = ∂r Fr
本章小结 本章小结
CQU
1、场的概念 标量场和矢量场的概念, 标量场和矢量场的概念,矢量场的分类以及每类矢量场的基本 特征。 特征。 2、场的三度计算 标量场的梯度 ∇f 、矢量场的散度 ∇ ⋅ F 和旋度 ∇ × F ; 要求牢记▽算符的矢量特性和微分特性; 要求牢记▽算符的矢量特性和微分特性; 牢固掌握在直角坐标系下的三度计算式,实施正确计算; 牢固掌握在直角坐标系下的三度计算式,实施正确计算; 在其它坐标系下,给定三度的计算式后, 计算场 在其它坐标系下,给定三度的计算式后,会计算场。 三度的计算式后 3、要会进行场的高阶计算 要做到此项,必须牢记矢量的点积、叉积,重要的矢量恒等式。 要做到此项,必须牢记矢量的点积、叉积,重要的矢量恒等式。 4、正确理解高斯散度定理和斯托克斯定理、正确认识赫姆 正确理解高斯散度定理和斯托克斯定理、 霍兹定理。 霍兹定理。
柱坐标求导公式

柱坐标求导公式柱坐标系是三维空间中的一种常见坐标系,其坐标由径向距离、极角和高度组成。
在数学和物理学中,需要对柱坐标系下的函数进行求导操作,以求得函数在柱坐标系下的导数。
本文将介绍柱坐标系下的求导公式及其推导过程。
基本概念柱坐标系下一个点的坐标用(ρ,θ,z)表示,其中: - ρ为点到z轴的距离,即径向距离; - θ为点在xy平面上与x轴正向的夹角,即极角; - z为点在z轴上的高度。
对于柱坐标系下的函数$ f(ρ,θ,z) $,我们希望求其对各个方向的导数。
求导公式对ρ的偏导数求函数f(ρ,θ,z)对ρ的偏导数,记为$ \frac{∂f}{∂ρ} $。
根据链式法则:$ \frac{∂f}{∂ρ} = \frac{∂f}{∂x} \frac{∂x}{∂ρ} + \frac{∂f}{∂y} \frac{∂y}{∂ρ} +\frac{∂f}{∂z} \frac{∂z}{∂ρ} $其中$ x = ρsinθ, y = ρcosθ, z = z $。
对上式中的各项进行求导,可得:$ \frac{∂x}{∂ρ} = sinθ, \fr ac{∂y}{∂ρ} = cosθ, \frac{∂z}{∂ρ} = 0 $代入原式,化简可得:$ \frac{∂f}{∂ρ} = sinθ\frac{∂f}{∂x} + cosθ\frac{∂f}{∂y} $对θ的偏导数求函数f(ρ,θ,z)对θ的偏导数,记为$ \frac{∂f}{∂θ} $。
同样根据链式法则:$ \frac{∂f}{∂θ} = \frac{∂f}{∂x} \frac{∂x}{∂θ} + \frac{∂f}{∂y} \frac{∂y}{∂θ} +\frac{∂f}{∂z} \frac{∂z}{∂θ} $其中$ x = ρsinθ, y = ρcosθ, z = z $。
对上式中的各项进行求导,可得:$ \frac{∂x}{∂θ} = ρcosθ, \frac{∂y}{∂θ} = -ρsinθ, \frac{∂z}{∂θ} = 0 $代入原式,化简可得:$ \frac{∂f}{∂θ} = ρcosθ\frac{∂f}{∂x} - ρsinθ\frac{∂f}{∂y} $对z的偏导数求函数f(ρ,θ,z)对z的偏导数,记为$ \frac{∂f}{∂z} $。
直角坐标系和圆柱坐标系的偏导数

直角坐标系和圆柱坐标系的偏导数在数学中,坐标系是用来描述一个点在平面或空间中位置的工具。
直角坐标系和圆柱坐标系是常见的两种坐标系,它们分别以不同的方式描述和表示点的位置。
在本文中,我们将探讨直角坐标系和圆柱坐标系中的偏导数的概念和计算方法。
直角坐标系直角坐标系是最为常见的坐标系。
它使用两个垂直的轴(通常是水平的 x 轴和垂直的 y 轴)来描述一个平面上的点的位置。
在直角坐标系中,我们可以用一个点的 x 坐标和 y 坐标来表示它的位置。
考虑一个二元函数 f(x, y),它在直角坐标系下表示一条曲面。
对于这个函数,我们可以计算它在某一点(xᵢ, yᵢ)处的偏导数。
偏导数是用来描述函数在某点处的变化率的概念。
在直角坐标系中,对于函数 f(x, y),它的偏导数可以用以下的方式计算:$f_x(x, y) = \\lim_{\\Delta x \\to 0} \\frac{f(x+\\Delta x, y) - f(x, y)}{\\Delta x}$ $f_y(x, y) = \\lim_{\\Delta y \\to 0} \\frac{f(x, y+\\Delta y) - f(x, y)}{\\Delta y}$ 其中,f x(x,y)表示函数 f 在点(x, y)处对 x 的偏导数,f y(x,y)表示函数 f 在点(x, y)处对 y 的偏导数。
计算偏导数时,我们固定一个坐标,对另一个坐标进行微小变化,并观察函数在这个点上的变化情况。
圆柱坐标系圆柱坐标系是一种三维坐标系,它使用一个极坐标平面和一个与其垂直的轴来描述一个点的位置。
在圆柱坐标系中,我们用一个点的极坐标半径 r、极角θ 和高度 z 来表示它的位置。
考虑一个三元函数g(r, θ, z),它在圆柱坐标系下表示一个曲面。
对于这个函数,我们可以计算它在某一点(rᵢ, θᵢ, zᵢ)处的偏导数。
在圆柱坐标系中,对于函数g(r, θ, z),它的偏导数可以用以下的方式计算:$g_r(r, θ, z) = \\lim_{\\Delta r \\to 0} \\frac{g(r+\\Delta r, θ, z) - g(r, θ,z)}{\\Delta r}$$g_θ(r, θ, z) = \\lim_{\\Delta θ \\to 0} \\frac{g(r, θ+\\Delta θ, z) - g(r, θ,z)}{\\Delta θ}$$g_z(r, θ, z) = \\lim_{\\Delta z \\to 0} \\frac{g(r, θ, z+\\Delta z) - g(r, θ,z)}{\\Delta z}$其中,g r(r,θ,z)表示函数 g 在点(r, θ, z)处对 r 的偏导数,gθ(r,θ,z)表示函数g 在点(r, θ, z)处对θ 的偏导数,g z(r,θ,z)表示函数 g 在点(r, θ, z)处对 z 的偏导数。
直角坐标和圆柱坐标转换偏导数的关系

直角坐标和圆柱坐标转换偏导数的关系在数学中,直角坐标和圆柱坐标是两种常见的坐标系。
直角坐标系使用x、y 和z轴来描述三维空间中的点,而圆柱坐标系使用径向(r)、极角(θ)和高度(z)来描述点的位置。
当我们需要在直角坐标系和圆柱坐标系之间进行转换时,了解偏导数的关系是非常重要的。
直角坐标系和圆柱坐标系的定义直角坐标系中,一个点的位置由三个坐标值确定,即(x, y, z)。
其中,x表示点在x轴上的距离,y表示点在y轴上的距离,z表示点在z轴上的距离。
这三个坐标值可以用直角坐标系中的直线距离表示。
圆柱坐标系中,一个点的位置由三个坐标值确定,即(r, θ, z)。
其中,r表示点到z轴的直线距离,θ表示点的极角,范围通常为0到2π,z表示点在z轴上的距离。
这三个坐标值可以用极坐标系的极径、极角和直角坐标系的高度来表示。
直角坐标和圆柱坐标之间的转换关系在直角坐标系和圆柱坐标系之间进行转换时,我们需要知道偏导数的关系。
偏导数可以用来描述一个函数在给定方向上的变化率。
对于直角坐标系到圆柱坐标系的转换,我们有以下关系:1.r的偏导数:–∂r/∂x = cos(θ)–∂r/∂y = sin(θ)–∂r/∂z = 02.θ的偏导数:–∂θ/∂x = -y/(x^2 + y^2)–∂θ/∂y = x/(x^2 + y^2)–∂θ/∂z = 03.z的偏导数:–∂z/∂x = 0–∂z/∂y = 0–∂z/∂z = 1对于圆柱坐标系到直角坐标系的转换,我们有以下关系:1.x的偏导数:–∂x/∂r = cos(θ)–∂x/∂θ = -r*sin(θ)–∂x/∂z = 02.y的偏导数:–∂y/∂r = sin(θ)–∂y/∂θ = r*cos(θ)–∂y/∂z = 03.z的偏导数:–∂z/∂r = 0–∂z/∂θ = 0–∂z/∂z = 1应用偏导数的关系在物理学、工程学和计算机图形学等领域中广泛应用。
例如,在计算机图形学中,我们常常需要将一个点的坐标在不同的坐标系下进行转换。
圆柱坐标系的坐标变量与直角坐标系坐标变量的偏导数

圆柱坐标系的坐标变量与直角坐标系坐标变量的偏导数引言在数学和物理学中,我们常常需要描述和计算空间对象的位置和运动。
直角坐标系是最常用的坐标系之一,但在一些特定的情况下,使用其他坐标系可以更方便地描述和计算问题。
圆柱坐标系是直角坐标系的一种常见替代,它由径向、极角和高度三个坐标变量组成。
本文将介绍圆柱坐标系的坐标变量与直角坐标系坐标变量之间的关系,并推导圆柱坐标系中的坐标变量对直角坐标系中的坐标变量的偏导数。
圆柱坐标系与直角坐标系的变换圆柱坐标系由三个坐标变量组成:r,$\\theta$和z。
r表示点到z轴的距离(称为径向),$\\theta$表示点到x轴的极角,z表示点在z轴上的高度。
我们可以通过下面的公式将圆柱坐标系的坐标变量转换为直角坐标系的坐标变量:$$ x = r \\cos(\\theta) $$$$ y = r \\sin(\\theta) $$z=z同样地,我们可以通过下面的公式将直角坐标系的坐标变量转换为圆柱坐标系的坐标变量:$$ r = \\sqrt{x^2 + y^2} $$$$ \\theta = \\arctan\\left(\\frac{y}{x}\\right) $$z=z坐标变量之间的偏导数坐标变量之间的偏导数是描述坐标系之间关系的重要工具。
在多元微积分中,我们常常使用偏导数来描述函数在不同方向上的变化率。
偏导数的定义是在其他变量保持不变的情况下,对某个变量求导。
在圆柱坐标系和直角坐标系的变换中,我们可以推导出坐标变量之间的偏导数关系。
首先,我们推导出r关于x和y的偏导数:$$ \\frac{\\partial r}{\\partial x} = \\frac{x}{\\sqrt{x^2 + y^2}} $$$$ \\frac{\\partial r}{\\partial y} = \\frac{y}{\\sqrt{x^2 + y^2}} $$接下来,我们推导出$\\theta$关于x和y的偏导数:$$ \\frac{\\partial \\theta}{\\partial x} = -\\frac{y}{x^2 + y^2} $$$$ \\frac{\\partial \\theta}{\\partial y} = \\frac{x}{x^2 + y^2} $$最后,由于z在圆柱坐标系和直角坐标系中保持不变,所以z关于x和y的偏导数均为0:$$ \\frac{\\partial z}{\\partial x} = 0 $$$$ \\frac{\\partial z}{\\partial y} = 0 $$总结通过推导,我们得到了圆柱坐标系的坐标变量与直角坐标系坐标变量之间的关系以及坐标变量之间的偏导数。
二阶偏导转为柱坐标

二阶偏导转为柱坐标二阶偏导转为柱坐标首先,我们需要先了解什么是二阶偏导数。
在数学中,偏导数是指多元函数中,对其中的一个自变量求导数时,将其它自变量视为不变量。
而二阶偏导数就是指在求一元函数的导数时,进行两次求导的结果。
转换为柱坐标系的建立,则是将常见的坐标系通过变量替换,转化为另一种坐标系。
柱坐标系主要由径向r、极角θ、高度z等三个变量组成,其建立方式是通过将直角坐标系中的x、y用极坐标变量r和θ代替,即x=r*cosθ,y=r*sinθ,再将z轴作为高度轴,即可得到柱坐标系。
对于如何将二阶偏导数转换为柱坐标系,我们可以通过利用柯西-黎曼方程来实现。
柯西-黎曼方程是一个极坐标系中的微分方程,其表达式为:∂f/∂θ=-i∂f/∂r。
通过这个式子,我们可以实现二阶偏导数的柱坐标系转化,具体步骤如下:1. 首先求出二阶偏导数∂^2f/∂x^2和∂^2f/∂y^2。
2. 将x和y用极坐标变量r和θ代替,即x=r*cosθ,y=r*sinθ。
3. 对于一阶偏导数,利用链式法则求出∂f/∂r和∂f/∂θ。
4. 对于二阶偏导数,再次利用链式法则求出∂^2f/∂r^2、∂^2f/∂θ^2和∂^2f/∂r∂θ。
5. 将得到的所有偏导数代入柯西-黎曼方程,并进行简化。
通过这个方法,我们可以实现将二阶偏导数在直角坐标系下的转化,变成在极坐标系下的形式,进而可以更好地进行求解和应用。
需要注意的是,柱坐标系转换过程中的求导过程相对较为复杂,需要我们对求导规则、链式法则以及函数的基本性质有较为深入的理解和熟练的运用。
因此,在应用过程中,我们需要对柯西-黎曼方程和柱坐标系的转换方法进行充分理解,并进行适当的练习和掌握,以确保运用的正确性和有效性。
总结起来,将二阶偏导数转换为柱坐标系可以帮助我们更好地理解和应用多元函数的导数,同时也能够更好地发挥坐标系的优势,深入挖掘数学知识的精髓。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
柱坐标系偏导
柱坐标系是三维坐标系的一种,它的坐标表示方法比较特殊,它以柱面半径$r$、极角$\theta$和高度$z$为坐标轴,来描述一个点在空间中的位置。
在柱坐标系中,我们可以通过一些基本的计算方法来求某个点的偏导数。
偏导数指的是函数在某一特定点上,沿着某个方向的导数。
我们可以分别对$r$、$\theta$和$z$三个方向来计算某一点上的偏导数。
对于$r$方向的偏导数,我们可以使用以下公式来计算:
$\cfrac{\partial f}{\partial r}=\cfrac{\partial
f}{\partial x}\cfrac{\partial x}{\partial r}+\cfrac{\partial f}{\partial y}\cfrac{\partial y}{\partial r}+\cfrac{\partial f}{\partial z}\cfrac{\partial z}{\partial r}$
其中,$f(x,y,z)$为三元函数,$x=r\cos\theta$,
$y=r\sin\theta$,$z=z$。
对于$\theta$方向的偏导数,我们可以使用以下公式来计算:
$\cfrac{\partial f}{\partial \theta}=\cfrac{\partial
f}{\partial x}\cfrac{\partial x}{\partial
\theta}+\cfrac{\partial f}{\partial y}\cfrac{\partial
y}{\partial \theta}+\cfrac{\partial f}{\partial
z}\cfrac{\partial z}{\partial \theta}$
其中,$f(x,y,z)$为三元函数,$x=r\cos\theta$,
$y=r\sin\theta$,$z=z$。
对于$z$方向的偏导数,我们可以使用以下公式来计算:
$\cfrac{\partial f}{\partial z}=\cfrac{\partial
f}{\partial x}\cfrac{\partial x}{\partial z}+\cfrac{\partial f}{\partial y}\cfrac{\partial y}{\partial z}+\cfrac{\partial f}{\partial z}\cfrac{\partial z}{\partial z}$
其中,$f(x,y,z)$为三元函数,$x=r\cos\theta$,
$y=r\sin\theta$,$z=z$。
需要注意的是,柱坐标系的偏导数计算方法与笛卡尔坐标系有区别。
在笛卡尔坐标系中,我们是通过对$x$、$y$、$z$三个方向分别求
偏导来计算某一点上的偏导数,而在柱坐标系中,则是通过$r$、
$\theta$、$z$三个方向分别计算。
此外,在柱坐标系中,使用偏导数进行求导时需要先转换为极坐
标系和直角坐标系之间的换元关系,再代入偏导数的公式中进行计算。
总之,在柱坐标系中进行偏导数的计算需要掌握一些基本的数学
知识,需要学习一定的数学基础知识。
但是,掌握了这些基础知识,
就可以对某点在某个方向上的导数进行计算,并能够更加深入地理解
柱坐标系的空间特性和性质。
