第九章 拉普拉斯变换PPT
合集下载
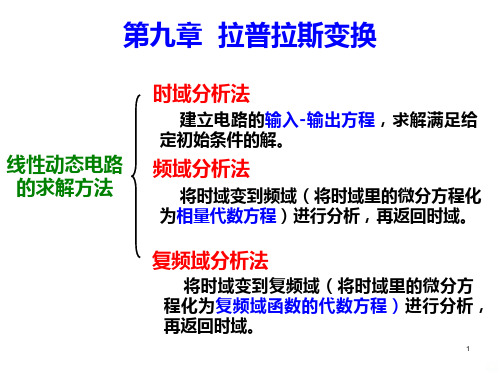
第9章 拉普拉斯变换

特别地,当
f (0) f (0) f (0) f ( n-1) (0) 0
时,
f ( n ) (t ) s n F ( s) ℒ
可以证明
( n ) (t ) s n ℒ
证 根据分部积分公式和拉氏变换公式
b
a
u d v uv | - v d u
9.2.3 积分性质
(1)象原函数的积分性质 若 ℒ f (t ) F (s),
则
F ( s) ℒ [ 0 f (t )dt ] s t -1 F ( s ) ℒ 0 f (t )dt s
t
一般地
1 ℒ [ 0 dt 0 dt 0 f (t )dt ] s n F (s)
sin k t e - st dt
k 所以 ℒ sin k t 2 s k2
Re s 0
即
k sin kt 2 2 s k
s 同理可得 cos kt 2 2 s k
2 如 ℒ sin 2t 2 s 4 s ℒ cos 3 t 2 s 9
此线性性质根据拉氏变换的定义就可得出.
2 相似性质
若 F ( s ) = ℒ f (t ) a 0 则 ℒ
f (at ) 1 F s a a
ℒ
-1
s F ( a ) af (at )
9.2.2 微分性质 (1)象原函数的微分性质
k - st e cos k tdt s 0
k - 2 s
- st - st k e sin k tdt e cos k t 0 0
电路PPT-拉普拉斯变换

)]
1
1 esT
F1(s)
對於本題脈衝序列
f1
(t
)
(t
)
(t
T 2)F1Fra bibliotek(s)
(1 s
1 s
esT
/
2
)
L[
f
(t
)]
1
1 esT
(1 1 esT/2) ss
11
s
( 1
esT
/
2
)
5.拉普拉斯的卷積定理
若: L[ f1(t)] F1(s) L[ f2(t)] F2(s)
返回 上頁 下頁
则:
返回 上頁 下頁
例 一些常用的變換
乘法運算變換
①對數變換 A B AB 為加法運算
lg A lg B lg AB
②相量法
正弦量 i1 i2 i
時域的正弦運算 變換為複數運算
相量 I1 I2 I
拉氏變換
對應
f(t)(時域原函數)
F(s)(頻域象函數)
返回 上頁 下頁
2. 拉氏變換的定義
原函數f(t) 用小寫字母表示,如 i(t), u(t)
返回 上頁 下頁
3.典型函數的拉氏變換
F(s) f (t)estdt 0
(1)單位階躍函數的象函數
f (t) (t)
F(s) L[ (t)] (t)estdt estdt
0
0
1 est s 0
1 s
返回 上頁 下頁
a1sm1 (s p1)n
am
F(s)
K11 s p1
(s
K12 p1)2
(s
K1n1 p1)n1
K1n (s p1)n
《拉普拉斯变换 》课件

详细描述
对于线性时不变控制系统,通过拉普拉斯变换分析其极点和零点,可以判断系 统的稳定性。如果所有极点都位于复平面的左半部分,则系统稳定;否则系统 不稳定。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
05
总结与展望
拉普拉斯变换的重要性和应用前景
拉普拉斯变换在数学、物理和工程领域中具有广泛的应用,是解决线性常微分方程 、积分方程、偏微分方程等数学问题的有力工具。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
03
拉普拉斯变换的运算技 巧
积分性质的运用
积分性质
如果函数f(t)的拉普拉斯变换为F(s), 那么对于任意常数a,函数f(at)的拉普 拉斯变换为aF(as)。
应用场景
在求解某些物理问题时,可能需要将 时间变量乘以常数,此时可以利用积 分性质简化拉普拉斯变换的运算。
REPORT
《拉普拉斯变换》 PPT课件
CATALOG
DATE
ANALYSIS
SUMMARY
目录
CONTENTS
• 拉普拉斯变换的基本概念 • 拉普拉斯变换的应用 • 拉普拉斯变换的运算技巧 • 拉普拉斯变换的实例分析 • 总结与展望
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
随着科学技术的发展,拉普拉斯变换的应用 领域也在不断拓展,例如在人工智能、机器 学习、数据科学等领域中的应用前景值得关 注。
未来需要进一步加强拉普拉斯变换 的理论研究,提高其在实际问题中 的应用效果,同时探索新的应用领 域,推动科学技术的发展。
对于线性时不变控制系统,通过拉普拉斯变换分析其极点和零点,可以判断系 统的稳定性。如果所有极点都位于复平面的左半部分,则系统稳定;否则系统 不稳定。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
05
总结与展望
拉普拉斯变换的重要性和应用前景
拉普拉斯变换在数学、物理和工程领域中具有广泛的应用,是解决线性常微分方程 、积分方程、偏微分方程等数学问题的有力工具。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
03
拉普拉斯变换的运算技 巧
积分性质的运用
积分性质
如果函数f(t)的拉普拉斯变换为F(s), 那么对于任意常数a,函数f(at)的拉普 拉斯变换为aF(as)。
应用场景
在求解某些物理问题时,可能需要将 时间变量乘以常数,此时可以利用积 分性质简化拉普拉斯变换的运算。
REPORT
《拉普拉斯变换》 PPT课件
CATALOG
DATE
ANALYSIS
SUMMARY
目录
CONTENTS
• 拉普拉斯变换的基本概念 • 拉普拉斯变换的应用 • 拉普拉斯变换的运算技巧 • 拉普拉斯变换的实例分析 • 总结与展望
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
随着科学技术的发展,拉普拉斯变换的应用 领域也在不断拓展,例如在人工智能、机器 学习、数据科学等领域中的应用前景值得关 注。
未来需要进一步加强拉普拉斯变换 的理论研究,提高其在实际问题中 的应用效果,同时探索新的应用领 域,推动科学技术的发展。
拉普拉斯变换-拉普拉斯变换表.ppt

2.2.2 拉普拉斯变换的定义
拉氏变换是否存在取决于定义的积分是否收敛。拉氏变 换存在的条件: ① 当t≥0时,f(t) 分段连续,只有有限个间断点; ② 当t →∞时,f(t) 的增长速度不超过某一指数函数,即
f (t ) Meat
式中:M、a为实常数。
在复平面上,对于Res >a的所有复数s (Res表示s的实部)都 使积分式绝对收敛,故Res >a是拉普拉斯变换的定义域, a称 为收敛坐标。
1 jt -jt st Lsin t sin t e dt e e e dt 0 2j 0 1 - ( s-j ) t -( s j ) t 1 1 1 e e dt 2 2j 0 2 j s-j s j s 2
st
0
1 2 s
2.2.3 典型时间函数的拉普拉斯变换
(4) 指数函数
指数函数表达式:
f (t ) e at
式中:a是常数。 其拉普拉斯变换为:
Le
at
0
e e dt e
at st 0
( s a ) t
1 dt sa
2.2.3 典型时间函数的拉普拉斯变换
若:函数 f(t) 各重积分的初始值均为零,则有
(n)
1 f (t )dt n F ( s) s
注:利用积分定理,可以求时间函数的拉普拉斯变换;利 用微分定理和积分定理,可将微分-积分方程变为代数方程。
2.2.4 拉普拉斯变换的基本性质 (5) 终值定理 若: L f (t ) F (s)
df (t ) L sF ( s) f (0) dt df (t ) 证明: df (t ) st st L e d t e df (t ) 0 dt 0 dt
电路原理-拉普拉斯变换PPT课件
收敛域为s平面的右半平面
[ (t)] 1
s
7
例2 求单位冲激函数 (t)的拉普拉斯象函数。
解:
[ (t)] (t)estdt 0
0
(t
)e
st
dt
(t)estdt
0
0
est t0 1
收敛域包括整个s平面。
[ (t)] 1
[sint (t)] s2 2
10
2. 微分定理 (differentiation theorem)
d dt
f (t)
s
f (t) f (0 )
*证明:
d
dt
f (t)
e st d f (t )dt
0
dt
e stdf (t )
f (t)
0
f ()
f (0 )
lim sF(s)
s0
f
(0 )
lim f (t) limsF(s)
t
s0
利用初值定理和终值定理,根据已知的象函数
F(s)可直接在复频域中确定其对应原函数f(t)的初值
和终值。
21
例8 设 f (t) (1 et ) (t) 验证初值定理和终值定理。
2!
t (t)
1 s3
t (n
n1
1)!
(
t
)
1 sn
1
1 sn
t n1 (n 1)!
(t )
16
4. 时域位移定理 (time-shift theorem)
拉普拉斯变换 PPT

F(s ) = ∫ f (t )e −st dt
0
∞
变量s叫做拉普拉斯算子。它为一复变数, 变量 叫做拉普拉斯算子。它为一复变数,即s=σ+jω。 叫做拉普拉斯算子 。
是一单位阶跃函数 时为1; 例:设f(t)是一单位阶跃函数,其定义为:t>0时为 ; t<0时为 是一单位阶跃函数,其定义为: 时为 时为 0。求此函数的拉普拉斯变换值。 。求此函数的拉普拉斯变换值。
∞
∫ f (t ) e
0
− st
dt = ∫ e
0
∞
− at
⋅e
− st
1 −( s + a )t ∞ dt = − e = 0 s+a
1 s +a
2、拉氏反变换 、
它是拉氏变换的F(s)求取 的运算。 F(s)的拉氏反变 求取f(t)的运算 它是拉氏变换的 求取 的运算。 的拉氏反变 换记为: 换记为:f(t)=L -1[F(s)]。并且由拉氏反变换积分求出, 。并且由拉氏反变换积分求出,
A1 A2 Ar + + ⋯+ , 2 r (s + si ) (s + si ) (s + si )
r −1
r−2
1 d2 ( s + si ) r X ( s ) = s = −s 2! ds2 i
1 d r −1 ( s + si ) r X ( s ) = s = −s ( r − 1) ! d s r − 1 i
= s n F ( s ) − s n −1 f (0 + ) − s n − 2 f (1) (0 + ) − ⋯ − f ( n −1) (0 + )
拉普拉斯变换(The Laplace Transform)课件

L
设
1 : X ( s) ( s 1)( s 2)
( s) 2
1 1 , ( s 1) ( s 2)
对X(s) 进行部分分式展开:
X ( s)
1 A B 1 1 ( s 1)( s 2) (s 1) (s 2) ( s 1) ( s 2)
S平面
j 0
j
s0 0 j0
0
• S平面上虚轴上的所有点代表整个周期 jt 复指数信号集 {e }
9.1 拉氏变换
一个信号x(t)的拉氏变换定义如下:
X (s) x(t )e dt ( where s j )
st
记作:
x(t ) X (s)
假设信号x(t)的拉氏变换X(s)没有多阶极 点,且分母多项式的阶次高于分子多项 式的阶次(有理真分式),那么X(s) 就可以展开成如下形式:
Ai X ( s) i 1 s ai
L {Ai /(s ai )}
1
M
Ai eait u(t )
Re{s} ai
Ai eait u(t ) Re{s} ai
性质3:如果x(t)是有限持续期,并 且是绝对可积的,那么ROC就是 整个s平面。
Im
s平面
Re
性质4:如果x(t)是右边信号,而且如果 Re{s} 0 这条线位于ROC内,那么 Re{s} 0 的全部s值都一定在ROC内。
0
Im s平面 Re
• 性质5:如果x(t)是左边信号,而且如果 • Re{s} 0 这条线位于ROC内,那么 • Re{s} 0 的全部s值都一定在ROC内。
1 2
设
1 : X ( s) ( s 1)( s 2)
( s) 2
1 1 , ( s 1) ( s 2)
对X(s) 进行部分分式展开:
X ( s)
1 A B 1 1 ( s 1)( s 2) (s 1) (s 2) ( s 1) ( s 2)
S平面
j 0
j
s0 0 j0
0
• S平面上虚轴上的所有点代表整个周期 jt 复指数信号集 {e }
9.1 拉氏变换
一个信号x(t)的拉氏变换定义如下:
X (s) x(t )e dt ( where s j )
st
记作:
x(t ) X (s)
假设信号x(t)的拉氏变换X(s)没有多阶极 点,且分母多项式的阶次高于分子多项 式的阶次(有理真分式),那么X(s) 就可以展开成如下形式:
Ai X ( s) i 1 s ai
L {Ai /(s ai )}
1
M
Ai eait u(t )
Re{s} ai
Ai eait u(t ) Re{s} ai
性质3:如果x(t)是有限持续期,并 且是绝对可积的,那么ROC就是 整个s平面。
Im
s平面
Re
性质4:如果x(t)是右边信号,而且如果 Re{s} 0 这条线位于ROC内,那么 Re{s} 0 的全部s值都一定在ROC内。
0
Im s平面 Re
• 性质5:如果x(t)是左边信号,而且如果 • Re{s} 0 这条线位于ROC内,那么 • Re{s} 0 的全部s值都一定在ROC内。
1 2
线性代数-拉普拉斯变换

一般地有F (n) (s) (1)n L[tn f (t)]. L[tn f (t)] (1)n F (n) (s).
求函数f (t) t sin kt的拉氏变换.
例4.
解:L[sin kt]
k
,
s2 k2
F[tn f (t)] ( j)n F (n) (s).
L[t
sin
kt]
d ds
F (s)ds, 或f (t) tL1[
F (s)ds].
t
s
s
推广:L[
f (t) tn ]
ds
s
ds ds
s
s
s F(s)ds.
2024/2/1
12
•
例5.计算积分0
sin t
t
dt.
解: sin t
1
0
t
dt 0
L[sin t]ds 0
s2
ds 1
arctan s
0
一般规定:在拉氏变换中f (t)均理解为:f (t) 0,t 0.
2024/2/1
4
例2.求指数函数f (t) eat的拉氏变换(a为实数).
解: L[ f (t)] eat estdt e(sa)tdt
0
0
1 e(sa) sa
0
1, sa
R(s a) 0
即:L[eat ] 1 , (Re(s) a). sa
18
几个常用函数的拉氏变换
L[ (t)] 1
L[u(t)] 1 , s
Re(s) 0
L[eat ] 1 , sa
Re(s) a
a L[sin at] s2 a2 ,
Re(s) 0
L[cos at] s , s2 a2
求函数f (t) t sin kt的拉氏变换.
例4.
解:L[sin kt]
k
,
s2 k2
F[tn f (t)] ( j)n F (n) (s).
L[t
sin
kt]
d ds
F (s)ds, 或f (t) tL1[
F (s)ds].
t
s
s
推广:L[
f (t) tn ]
ds
s
ds ds
s
s
s F(s)ds.
2024/2/1
12
•
例5.计算积分0
sin t
t
dt.
解: sin t
1
0
t
dt 0
L[sin t]ds 0
s2
ds 1
arctan s
0
一般规定:在拉氏变换中f (t)均理解为:f (t) 0,t 0.
2024/2/1
4
例2.求指数函数f (t) eat的拉氏变换(a为实数).
解: L[ f (t)] eat estdt e(sa)tdt
0
0
1 e(sa) sa
0
1, sa
R(s a) 0
即:L[eat ] 1 , (Re(s) a). sa
18
几个常用函数的拉氏变换
L[ (t)] 1
L[u(t)] 1 , s
Re(s) 0
L[eat ] 1 , sa
Re(s) a
a L[sin at] s2 a2 ,
Re(s) 0
L[cos at] s , s2 a2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3. 双边信号的ROC可以是任意两相邻极点之间
的带形区域。
1 例3. X ( s ) 2 s 3s 2 1 1 s 1 s 2
j
2
1
可以形成三种 ROC:
1) ROC: Re[ s] 1
2) ROC:Re[ s] 2
此时x(t ) 是右边信号。 此时 x(t )是左边信号。 此时x(t ) 是双边信号。
j 时,就是连续时间傅里叶变换。
一.双边拉氏变换的定义:
X (s) x(t )e st d,其中 s j 。
s 若 0,
j 则有: X ( j ) x(t )e jt dt
这就是 x(t ) 的傅里叶变换。 表明:连续时间傅里叶变换是双边拉普拉斯变换 在 0 或是在 j 轴上的特例。
由于 X (s)
x(t )e e
t jt
dt [ x(t )e t ]e jt dt
F[ x(t )e [
t
]
所以拉氏变换是对傅里叶变换的推广, x(t ) 的 拉氏变换就是 x (t )e t 的傅里叶变换。只要有合 适的 存在,就可以使某些本来不满足狄里赫利 条件的信号在引入 e t 后满足该条件。即有些信 号的傅氏变换不收敛而它的拉氏变换存在。这表 明拉氏变换比傅里叶变换有更广泛的适用性。
第9章 拉普拉斯变换
THE LAPLACE TRANSFORM
本章基本内容:
1. 双边拉普拉斯变换; 2. 双边拉普拉斯变换的收敛域; 3. 零极点图; 4. 双边拉普拉斯变换的性质; 5. 系统函数; 6. 单边拉普拉斯变换;
9.0 引言 Introduction
傅里叶分析方法之所以在信号与LTI系统分析
显然 X ( s ) 在 s a 也有一阶零点,由于零极 点相抵消,致使在整个S平面上无极点。 例2. x(t ) e
b t
x(t ) e u (t ) e u (t )
bt
bt
1 bt e u (t ) , sb
bt
Re[ s] b
b
j
b
1 e u (t ) , Re[ s] b s b
当 b 0 时,上述ROC有公共部分,
1 1 X ( s) s b s b
不存在。
b Re[s] b
当b 0 时,上述 ROC 无公共部分,表明 X ( s)
当 X ( s)是有理函数时,其ROC总是由X (s) 的
极点分割的。ROC必然满足下列规律:
1. 右边信号的ROC一定位于 X ( s) 最右边极点 的右边。 2. 左边信号的ROC一定位于 X ( s) 最左边极点 的左边。
1 1 X ( s) s 1 s 2
1 ROC : Re[s ] 1 e t u (t ) s 1 1 ROC : Re[s ] 2 e2t u (t ) s2
x(t ) e2t u(t ) e t u (t )
留数法(当 X ( s) 是有理函数时): 1. 求出 X ( s) 的全部极点。 2. 求出 X ( s )e st 在 ROC 左边的所有极点处的留 数之和,它们构成了x(t ) 的因果部分。 3. 求出 X ( s )e st 在 ROC 右边的所有极点处的留 数之和,并加负号,它们构成了 x(t ) 的反因果 部分。
可以归纳出ROC的以下性质:
1. ROC是 S 平面上平行于 j 轴的带形区域。 2. 在ROC内无任何极点。 3. 时限信号的ROC是整个 S 平面。
4. 右边信号的ROC位于S平面内一条平行于 j
轴的直线的右边。
若 x(t ) 是右边信号, T t , 0 在ROC内, 则有 x(t )e 0t 绝对可积,即:
j
Re[ s] 1
2 1
可见:拉氏变换的收敛域是各个收敛域的公共部
分。ROC总是以平行于 j 轴的直线作为边界的,
ROC的边界总是与 X ( s) 的分母的根相对应的。
(s ) N (s) M 若 X ( s) 是有理函数 X ( s ) D( s) (s )
i i i i
分子多项式的根称为零点,分母多项式的根 称为极点。 将 X ( s) 的全部零点和极点表示在S平面上,
就构成了零极点图。零极点图及其收敛域可以
表示一个 X ( s) ,最多与真实的 X ( s) 相差一个常
数因子 M 。
因此,零极点图是拉氏变换的图示方法。
9.2 拉氏变换的收敛域
The Region of Convergence for Laplace Transforms
1 st 1 st e s 1 u( t ) e s2 s 1 t 2 t e u ( t ) e u (t )
s 2
u (t )
9.4 由零极点图对傅里叶变换几何求值
t 2t
j
1
X (s) e e dt e e dt
t st 2t st 0 0
1 e u( t ) , Re[s ] 1 s 1
t
j
2
1 e u (t ) , Re[s ] 2 s2
2 t
1 1 2s 3 X ( s) 2 , s 1 s 2 s 3s 2
0
T
at
0t T
其它 t
at st
X ( s) e e dt
0
e
0
T
( s a )t
1 ( s a )T dt [1 e ] sa
X ( s )有极点
s a
考查零点,令 e ( s a )T 1
2 k(k为整数) 得 s a j T
0 在
T
x(t )e
1t
dt
T
x(t )e
0t (1 0 )t
e
dt
e
(1 0 )T
T
x(t )e 0t dt
表明 1 也在收敛域内。
6. 双边信号的ROC如果存在,一定是 S 平面内
平行于 j 轴的带形区域。
e 例1. x (t )
例1.
x(t ) e u (t )
X ( s) e e dt e
at st 0 0 ( s a )t
at
1 dt sa
在 Re[s ] a 时,积分收敛。 当 a 0 时, x(t ) 的傅里叶变换存在
X ( j ) e e
3) ROC: 2 Re[ s] 1
9. 3 拉普拉斯反变换
The Inverse Laplace Transform 一.定义: 由 X (s) x(t )e st dt 若 s j 在ROC内,则有:
X ( j ) x(t )e t e jt dt F[ x(t )e t ] [
X ( s)e st ds
X ( s )的反变换
x(t )
1 2 j
j
j
拉氏反变换表明:
可以被分解成复振幅为 1 X ( s )ds x(t ) 2 j 的复指数信号e st 的线性组合。
二.拉氏反变换的求法: 对有理函数形式的 X ( s)求反变换一般有两种方 法,即部分分式展开法和留数法。 部分分式展开法: 1. 将 X ( s) 展开为部分分式。 2. 根据 X ( s) 的ROC,确定每一项的ROC 。 3. 利用常用信号的变换对与拉氏变换的性质, 对每一项进行反变换。
0
at j t
1 dt a j
(a 0)
显然,在 a 0 时,拉氏变换收敛的区域为
Re[s ] a ,包括了 0 (即 j 轴)。
比较 X ( s ) 和 X ( j ) ,显然有
X (s)
s j
X ( j )
x(t ) e at u (t ) u (t ) 当 a 0时, 1 Re[ s] 0 可知 u (t ) s
T
x(t )e
0t
dt
x(t )e1t dt
0t ( 1 0 ) t
若 1 0 ,则
T
T
x(t )e e
( 1 0 )T
e
dt dt
表明 1 也在收敛域内。
T
x(t )e
0 t
5. 左边信号的ROC位于S平面内一条平行于j 轴的直线的左边。 若x(t )是左边信号,定义于 ( ,T , ROC 内, 1 0,则
x(t )e
t
1 2
X ( j )e jt d
t jt
1 x(t ) 2
1 X ( j )e e d 2
X (s)e st d
由 s j 得 ds jd
当 从 时,
s 从 j j
1 例1. X ( s ) ( s 1)( s 2)
确定其可能的收敛域及所对应信号的属性。
s 极点: 1, s 2
j
2 1 2 1
j
2 1
j
右边信号
左边信号
双边信号
1 例2. X ( s ) ( s 1)( s 2)
