05-4结构力学 第五章 超静定结构的内力和位移计算(5.5节 力矩分配法)ok
合集下载
结构力学二5-超静定结构的内力与位移计算

X1=1
X2=1
M2
P
X3=1
M3
MP
另一解法
P X1 X2 X3
M1
13 31 0
2 P 3 P 0
11 X 1 12 X 2 1P 0 21 X 1 22 X 2 23 X 3 0 X X 0 32 2 33 3
i 1X1+ i 2X2+
… …
+ 1iXi+
+ i iXi+
… …
+ 1nXn+△1P=0
+ i nXn+△iP=0
…………………………………………………………… n1X1+ n2X2+ … + niXi+ … + nnXn+△nP=0
这便是n次超静定结构的力法典型(正则)方程。式中 Xi为多余未知力, i i为主系数,i j(i≠j)为副系数, △iP 为常数项(又称自由项)。
4. 力法典型(正则)方程系数和自由项的计算
典型方程中的各项系数和自由项,均是基本结构在已知力 作用下的位移,可以用计算位移的方法计算。对于平面结构 ,这些位移的计算公式为
对不同结构选取不同项计算。系数和自由项求得后, 代入典型方程即可解出各多余未知力。
力法的计算步骤和示例 1. 示例 n=2(二次超静定) 选择基本结构如图示 C
3. 力法方程及系数的物理意义 (1)力法方程的物理意义为:基本结构在全部多余未知 力和荷载共同作用下,基本结构沿多余未知力方向上的位移 ,应与原结构相应的位移相等。 (2)系数及其物理意义:下标相同的系数 i i 称为主系数( 主位移),它是单位多余未知力 单独作用时所引起的沿 其自身方向上的位移,其值恒为正。 系数 i j(i≠j)称为副系数(副位移),它是单位多余未知力 单独作用时所引起的沿 Xi方向上的位移,其值可能为 正、为负或为零。据位移互等定理,有 i j= j i △i P称为常数项(自由项)它是荷载单独作用时所引起的沿Xi 方向的位移。其值可能为正、为负或为零。 上述方程的组成具有规律性,故称为力法典型方程。
结构力学 力矩分配法计算超静定结构

知识链接
力法和位移法是求解超静定结构的两种基本方法。两种方法的共同特点都是 要列方程和解联立方程,计算烦琐。而力矩分配法是建立在位移法基础上的一 种渐近解法,计算过程按照重复步骤进行,结果逐渐接近真实解答。它无须解 联立方程而直接计算出杆端弯矩,方法简便,适合手算。适用范围是连续梁和 无侧移刚架的内力计算。
情景二 用力矩分配法计算连续梁 学习能力目标
掌握力矩分配法计算连续梁并绘制弯矩图。
项目表述
运用力矩分配法计算多跨连续梁结构。
学习进程
情景二 用力矩分配法计算连续梁
项目实施
案例 3 – 17 图 3 – 62a 所示为两跨梁,试用力矩分配法求杆端弯矩,并作 M 图。
解答:(1)计算分配系数 同一结点各杆分配系数之和等于 1,把算好的μ 值填在表格 3 – 5中B结点处。 (2)计算固端弯矩(查表 3 – 4) (3)放松刚结点 B 进行力矩分配 (4)计算传递弯矩 (5)计算杆端弯矩 把同一杆端的固端弯矩、分配弯矩和传递弯矩相加(代数和),即得杆端弯
情景一 力矩分配法的基本原理和要素
知识链接
加于刚结点 1 的外力矩按分配系数分配给各杆的 1 端(近端),称 其 为分配弯矩。
3.传递系数 C 如图 3 – 60 所示,当外力矩 M 加于结点 1 时,该结点发生转角.1 , 于是各杆近端和远端都将产生杆端弯矩,这些杆端弯矩值如下
情景一 力矩分配法的基本原理和要素
解答:① 求分配系数。 ② 锁住结点 B、C,求各杆的固端 M。 ③ 先放松结点 C,按单结点直接把M=150kN.m进行分配、传递,此时 C
暂时平衡,将结果填入表中。求出此时结点B的不平衡力矩。 ④ 再放松结点 B,将( - MB )进行分配、传递,此时 B 暂时平衡,而由
力法和位移法是求解超静定结构的两种基本方法。两种方法的共同特点都是 要列方程和解联立方程,计算烦琐。而力矩分配法是建立在位移法基础上的一 种渐近解法,计算过程按照重复步骤进行,结果逐渐接近真实解答。它无须解 联立方程而直接计算出杆端弯矩,方法简便,适合手算。适用范围是连续梁和 无侧移刚架的内力计算。
情景二 用力矩分配法计算连续梁 学习能力目标
掌握力矩分配法计算连续梁并绘制弯矩图。
项目表述
运用力矩分配法计算多跨连续梁结构。
学习进程
情景二 用力矩分配法计算连续梁
项目实施
案例 3 – 17 图 3 – 62a 所示为两跨梁,试用力矩分配法求杆端弯矩,并作 M 图。
解答:(1)计算分配系数 同一结点各杆分配系数之和等于 1,把算好的μ 值填在表格 3 – 5中B结点处。 (2)计算固端弯矩(查表 3 – 4) (3)放松刚结点 B 进行力矩分配 (4)计算传递弯矩 (5)计算杆端弯矩 把同一杆端的固端弯矩、分配弯矩和传递弯矩相加(代数和),即得杆端弯
情景一 力矩分配法的基本原理和要素
知识链接
加于刚结点 1 的外力矩按分配系数分配给各杆的 1 端(近端),称 其 为分配弯矩。
3.传递系数 C 如图 3 – 60 所示,当外力矩 M 加于结点 1 时,该结点发生转角.1 , 于是各杆近端和远端都将产生杆端弯矩,这些杆端弯矩值如下
情景一 力矩分配法的基本原理和要素
解答:① 求分配系数。 ② 锁住结点 B、C,求各杆的固端 M。 ③ 先放松结点 C,按单结点直接把M=150kN.m进行分配、传递,此时 C
暂时平衡,将结果填入表中。求出此时结点B的不平衡力矩。 ④ 再放松结点 B,将( - MB )进行分配、传递,此时 B 暂时平衡,而由
结构力学超静定结构计算

M AC ? iAC? A ? SAC? A
SAB= 3i
M A1B ?
SAB= i
SAB M S
A
MAD
C
M
? MAB
m? 0
? M AD ? 3iAD? A ? SAD? A
1
M AC ?
M ? (SAB ? SAC ? SAD )? A
SAC M S
A
MAC
A
? ? A
?
SAB ?
M SAC
?
法相同,即都假设对杆端顺时针旋转为正号、对结点
或附加刚臂逆时针旋转为正号。作用于结点的外力偶 荷载、作用于附加刚臂的约束反力矩,也假定为对结
点或附加刚臂顺时针旋转为正号。
一、转动刚度 S:表示杆端对转动的抵抗能力。
在数值上 = 仅使杆件近端产生单位转角时所需在杆端施加 的力矩。
SAB=4i
1
SAB=3i
A
?A
B
CAB ?
M BA M AB
?
0
? MAB= iAB A
A
?A
MBA = - iAB ?A
B
CAB ?
M BA M AB
?
?1
在结点上的外力矩按各杆分配系数分配给各杆近端截面,各杆远 端弯矩分别等于各杆近端弯矩乘以传递系数。
单结点的力矩分配
——基本运算
A MAB
B
MBA
= MBC
MB
固端弯矩带本身符号 C
-MC
锁住1结点,用单结点
1
2
+
的力矩分配法,对2结 点的不平衡力矩进行分
…
配。
§2 多结点的力矩分配 ——渐近运算
SAB= 3i
M A1B ?
SAB= i
SAB M S
A
MAD
C
M
? MAB
m? 0
? M AD ? 3iAD? A ? SAD? A
1
M AC ?
M ? (SAB ? SAC ? SAD )? A
SAC M S
A
MAC
A
? ? A
?
SAB ?
M SAC
?
法相同,即都假设对杆端顺时针旋转为正号、对结点
或附加刚臂逆时针旋转为正号。作用于结点的外力偶 荷载、作用于附加刚臂的约束反力矩,也假定为对结
点或附加刚臂顺时针旋转为正号。
一、转动刚度 S:表示杆端对转动的抵抗能力。
在数值上 = 仅使杆件近端产生单位转角时所需在杆端施加 的力矩。
SAB=4i
1
SAB=3i
A
?A
B
CAB ?
M BA M AB
?
0
? MAB= iAB A
A
?A
MBA = - iAB ?A
B
CAB ?
M BA M AB
?
?1
在结点上的外力矩按各杆分配系数分配给各杆近端截面,各杆远 端弯矩分别等于各杆近端弯矩乘以传递系数。
单结点的力矩分配
——基本运算
A MAB
B
MBA
= MBC
MB
固端弯矩带本身符号 C
-MC
锁住1结点,用单结点
1
2
+
的力矩分配法,对2结 点的不平衡力矩进行分
…
配。
§2 多结点的力矩分配 ——渐近运算
自考结构力学 超静定结构的内力和位移

3、力法基本方程-
D11 d 11 X 1 d 11 X 1 D1P 0
D11 X 1 D1 p 0
一、力法基本思路 有多余约束是超静定与静定的根本区别,因此,解决 多余约束中的多余约束力是解超静定的关键。
力法的基本体系
D1=0 D11=1
D11 + D1P =0 d11x1+ D1P =0
作单位和荷载弯矩图
FP F Pa
求系数、建立力法方程并求解
X2 5 FP X1 4 FP 0 仅与刚 X1 6 4 96 11 度相对 X1 5X2 FP 3F 值有关 P 0 X2 4 6 16 88
4 FP X1 11 X 2 3 FP 88
基本方程的物理意义?
X1
X2
a
b
l
a
b
基本结构在支座位移和基本未知力共同作用下,在基本 未知力作用方向上产生的位移与原结构的位移完全相等。
d11 X 1 d12 X 2 D1c 0 d 21 X 1 d 22 X 2 D 2 c
h
X1 1
1
1 l
X2 1
注意
q
1、基本体系有多种选择;
X1
q
q
X1
EI
1
q q
D1 p
q
X1 X1
D1 p
)d
d 11 X 1
11
X1
X1
(a) 2、系数和自由项的计算 3、采用叠加法绘制内力图
(b)
(c)
基本原理举例
例1. 求解图示单跨梁 原结构
待解的未知问题
D11 d 11 X 1 d 11 X 1 D1P 0
D11 X 1 D1 p 0
一、力法基本思路 有多余约束是超静定与静定的根本区别,因此,解决 多余约束中的多余约束力是解超静定的关键。
力法的基本体系
D1=0 D11=1
D11 + D1P =0 d11x1+ D1P =0
作单位和荷载弯矩图
FP F Pa
求系数、建立力法方程并求解
X2 5 FP X1 4 FP 0 仅与刚 X1 6 4 96 11 度相对 X1 5X2 FP 3F 值有关 P 0 X2 4 6 16 88
4 FP X1 11 X 2 3 FP 88
基本方程的物理意义?
X1
X2
a
b
l
a
b
基本结构在支座位移和基本未知力共同作用下,在基本 未知力作用方向上产生的位移与原结构的位移完全相等。
d11 X 1 d12 X 2 D1c 0 d 21 X 1 d 22 X 2 D 2 c
h
X1 1
1
1 l
X2 1
注意
q
1、基本体系有多种选择;
X1
q
q
X1
EI
1
q q
D1 p
q
X1 X1
D1 p
)d
d 11 X 1
11
X1
X1
(a) 2、系数和自由项的计算 3、采用叠加法绘制内力图
(b)
(c)
基本原理举例
例1. 求解图示单跨梁 原结构
待解的未知问题
05-2结构力学 第五章 超静定结构的内力和位移计算(5.4节 弹性中心法)ok
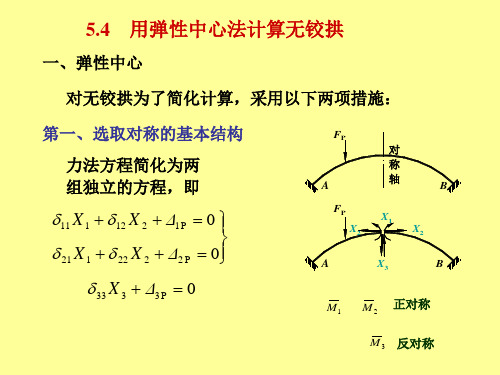
三、两铰拱的计算
q F y q F
j
(x, y) x
f
f
l 两铰拱 力法方程为
l
力法基本结构
X1
11 X1 1P 0
计算柔度系数和自由项时,一般可略去剪力的影响。仅当f<l/5时,才在11中考虑轴力的 影响。即 yM P FN21 M 12 M M ds 11 ds ds 1P 1 P ds 1 P I EI EA EI X1 y2 cos2 j 11 I ds A ds M1 y FN1 cosj
三、两铰拱的计算
q F y q F
j
(x, y) x
f
f
l 两铰拱
l
力法基本结构
X1
X1
1P 11
yM P I ds y2 cos2 j ds ds I A
解出X1后,由叠加法,可求出任一截面的内力。计算公式与三铰拱类似,即
M M 0 X1 y
FS FS0 cosj X1 sin j
4.47qR3 EI X1 0.87qR 2 11 EI 5.14R Δ1P
X2 Δ2P
22
2.43qR4 EI 1.14qR 3 EI 2.04R
(4)根据叠加公式,求得
M A X 1 X 2 ( y yS ) M P
2 2 qR q ( 2 R ) 0.87qR 2 1.14qR(2 R 0.81R) [ ] 2 2
1P
2 P
M 1M P ds EI M 2M P ds EI
一般情况下,积分无法直接积出来,可 采用数值积分,用求和来代替。
超静定结构的力矩分配法计算

M
F B
)
M B D
BD(
M
F B
)
5、传递系数 远端为固定支座:
1 C= 2 远端为铰支座: C =0
远端为双滑动支座: C = -1
6、远端传递弯矩 近端杆端分配弯矩可通过固端弯矩按比例分配得到, 而远端传递弯矩则可通过近端分配弯矩得到。
M AB CBAM B A
M CB CBCM B C
BC
S BC SB
BD
S BD SB
一个杆件的杆端分配系数等于自身杆端转动刚度 除以杆端结点所连各杆的杆端转动刚度之和。
各结点分配系数之和等于1 BA BC BD 1
4、近端分配弯矩
将不平衡力矩变号后按比例分配得到各杆的近端分 配弯矩。
M B A
BA (
M
F B
)
M B C
BC (
M D B CBDM B D
建筑力学
力矩分配法中结点弯矩正负号规定: 结点弯矩使结点逆时针转为正 。
1.2 力矩分配法的要素
1、固端弯矩、固端剪力 固端弯矩是荷载引起的杆件在分配结点处固定时产 生的杆端弯矩 固端剪力是荷载引起的杆件在分配结点处固定时产 生的杆端剪力
固端弯矩、固端剪力可通过查表13.1获得 i称为线刚度: i EI
l
其中:EI是杆件的抗弯刚度;l 是杆长。
序 号
梁的简图
1
2
3
杆端弯矩
MAB
MBA
4i
i EI
2i
l
ql2
ql 2
12 12
杆端剪力
FQAB
FQBA
6i 6i
l
l
ql 2
ql 2
结构力学课件 第五章 静定结构位移计算
N P l EA FN FNP
钢筋 混凝土
-4.74FP -1.58
Ab Ab 0.75Ab
Ag 3Ag 2Ag
1.97FPl/AbEb 1.84FPl/AbEb 0 0 0.63FPl/AgEg 0.5FPl/AgEg
CD DE CE
-4.42FP -1.58
0 0
0.263l
0.088l 0.278l
• 结构整体变形和支座移动共同产生的总位移计算
( FN FQ Mk)ds FR K c K
欲求的实际位移
cK
实际发生的已知位移
FN
FQ
M
FR K
虚设单位力作用下产生的力
§5-3 荷载作用下的位移计算
• 计算公式 • 计算步骤 • 各类结构位移计算公式
(M k FN FQ)ds
kFQ FQP FN FN P MMP ds ds ds EI EA GA
欲求的实际位移 M P FNP FQP 实际荷载作用下产生的内力
M
FN
FQ
虚设单位力作用下产生的内力
每一积分式的两个内力若使杆件变形一致,则其乘积取正号, 反之则取负号。
计算结果若 0 若 0
Ay0 EI
ql 2
MP
1
1
M
B
ql 2 ql 2
1
1
1
q
l
ql
l
ql 2
FN P
1
1
FN
FN FNP l FN FNP N ds EA EA
N 1 ql ql 2 N 1 l () M EA 2 2 EA
结构力学超静定结构的内力和位移计算PPT课件
5
第5页/共29页
力法方程中的柔度系数与自由项,都是力法基本结构在已知力作用下的位 移,相应的计算公式为
dii
M
2 i
ds
EI
FN2i ds EA
kFS2i ds GA
dij d ji
MiM j ds EI
FNi FNj ds EA
kFSi FSj ds GA
FNitl
Dt h
M i ds
13
第13页/共29页
例题5-7. 图示刚架,外侧温度升高20oC,内侧温度升高30oC,试用力法求解并作出M图。已 知杆件横截面为矩形截面,高度h=l/10,EI=常数,材料线膨胀系数为。
原结构
力法基本结构
FN1
M1
M图
d11 X1 D1t 0
d11
1 EI
(1 l 2
d n1 X1 d n2 X 2 d nn X n DnP Dn 0
对于力法典型方程,应注意理解与掌握以下几点: (1) 力法典型方程的物理意义,是多余约束处的位移方程; (2) dij称为结构的柔度系数,其定义是j方向的单位力引起的i方向的位移,第1个下标表示 发生位移的位置,第2个下标表示产生位移的原因。位移互等定理,dij=dji。主柔度系数必 为正,即dii>0。副柔度系数dij可为正、负或0。柔度系数为结构的固有特性,与荷载等外 界因素无关; (3) 自由项DiP的物理意义是,荷载单独作用在力法基本结构上产生的沿Xi方向的位移,可 为正、负或0; (4) 力法方程也称为柔度方程,力法也称为柔度法;
D1P
X1 2d EA
FN
若将上弦杆DE去掉,其基本结构如示。此时,在X1与荷载共同作用下,D、E两点沿轴方向的相对线位移不
第5页/共29页
力法方程中的柔度系数与自由项,都是力法基本结构在已知力作用下的位 移,相应的计算公式为
dii
M
2 i
ds
EI
FN2i ds EA
kFS2i ds GA
dij d ji
MiM j ds EI
FNi FNj ds EA
kFSi FSj ds GA
FNitl
Dt h
M i ds
13
第13页/共29页
例题5-7. 图示刚架,外侧温度升高20oC,内侧温度升高30oC,试用力法求解并作出M图。已 知杆件横截面为矩形截面,高度h=l/10,EI=常数,材料线膨胀系数为。
原结构
力法基本结构
FN1
M1
M图
d11 X1 D1t 0
d11
1 EI
(1 l 2
d n1 X1 d n2 X 2 d nn X n DnP Dn 0
对于力法典型方程,应注意理解与掌握以下几点: (1) 力法典型方程的物理意义,是多余约束处的位移方程; (2) dij称为结构的柔度系数,其定义是j方向的单位力引起的i方向的位移,第1个下标表示 发生位移的位置,第2个下标表示产生位移的原因。位移互等定理,dij=dji。主柔度系数必 为正,即dii>0。副柔度系数dij可为正、负或0。柔度系数为结构的固有特性,与荷载等外 界因素无关; (3) 自由项DiP的物理意义是,荷载单独作用在力法基本结构上产生的沿Xi方向的位移,可 为正、负或0; (4) 力法方程也称为柔度方程,力法也称为柔度法;
D1P
X1 2d EA
FN
若将上弦杆DE去掉,其基本结构如示。此时,在X1与荷载共同作用下,D、E两点沿轴方向的相对线位移不
结构力学 第五章 力法
目,即为超静定次数。
(2)确定超静定次数的方法——通过去掉多余约束来
确定。(去掉n个多余约束,即为n次超静定)。
(3)去掉(解除)多余约束的方式 a、撤去一个活动铰支座、去掉或切断一根链杆——去
掉1个约束(联系);
X1
§ 5-1 超静定结构概述和力法基本概念
b、去掉一个单铰或一个固定铰支座—— 去掉2个约束;
X 1 Δ1 p 0 X Δ n np
(3)最后弯矩
M X1 M 1 X 2 M 2 X n M n
§ 3-2 力法的基本原理及典型方程
力法基本思路小结
解除多余约束,转化为静定结构。多余约 束代以多余未知力——基本未知力。 分析基本结构在单位基本未知力和外界因 素作用下的位移,建立位移协调条件——力 法方程。
单独作用于基本结构时,所引起的沿Xi方向的位移,
可为正、负或零,且由位移互等定理:δi j =δj i 自由项ΔiP ——荷载FP单独作用于基本体系时, 所引起Xi方向的位移,可正、可负或为零。
§ 3-2 力法的基本原理及典型方程 (2)典型方程的矩阵表示
δ11 δn1
δ1n δnn
3
0.393ql
0.464ql 0.607ql
§ 3-2 力法的基本原理及典型方程
力法基本原理:把去掉原结构上的多 余联系后所得的静定结构作为基本结构, 以多余约束力作为基本未知量,根据原 结构在多余联系处的变形条件列力法方 程,解之即得多余约束力;而以后的计 算与静定结构相同。必须指出,基本结 构的选取虽然可以不同,但它必须是几 何不变的。否则不能用作计算超静定结 构的计算图形。支反力数 目); j(节点数)
(2)确定超静定次数的方法——通过去掉多余约束来
确定。(去掉n个多余约束,即为n次超静定)。
(3)去掉(解除)多余约束的方式 a、撤去一个活动铰支座、去掉或切断一根链杆——去
掉1个约束(联系);
X1
§ 5-1 超静定结构概述和力法基本概念
b、去掉一个单铰或一个固定铰支座—— 去掉2个约束;
X 1 Δ1 p 0 X Δ n np
(3)最后弯矩
M X1 M 1 X 2 M 2 X n M n
§ 3-2 力法的基本原理及典型方程
力法基本思路小结
解除多余约束,转化为静定结构。多余约 束代以多余未知力——基本未知力。 分析基本结构在单位基本未知力和外界因 素作用下的位移,建立位移协调条件——力 法方程。
单独作用于基本结构时,所引起的沿Xi方向的位移,
可为正、负或零,且由位移互等定理:δi j =δj i 自由项ΔiP ——荷载FP单独作用于基本体系时, 所引起Xi方向的位移,可正、可负或为零。
§ 3-2 力法的基本原理及典型方程 (2)典型方程的矩阵表示
δ11 δn1
δ1n δnn
3
0.393ql
0.464ql 0.607ql
§ 3-2 力法的基本原理及典型方程
力法基本原理:把去掉原结构上的多 余联系后所得的静定结构作为基本结构, 以多余约束力作为基本未知量,根据原 结构在多余联系处的变形条件列力法方 程,解之即得多余约束力;而以后的计 算与静定结构相同。必须指出,基本结 构的选取虽然可以不同,但它必须是几 何不变的。否则不能用作计算超静定结 构的计算图形。支反力数 目); j(节点数)
超静定结构-力法、位移法、有侧移钢架
例2:用位移法求解图示刚架
q=42kN/m
A i=3
B i=3
CD i=3
i=2
i=2
5m
E
F
q=42kN/m
1
2 基本结构
基本未知量
基本体系
6m
6m
2m
原结构位移 =Δ1引起的位移 +Δ2引起的位移 +荷载引起的位移
原结构内力 =Δ1引起的内力 +Δ2引起的内力 +荷载引起的内力
F1 F11 F12 F1P k111 k122 F1P 0
q=42kN/m
A i=3
B i=3
i=2 E
CD i=3
i=2
5m
F
6m
6m
2m
12
12
6
6 6
12
M1
1ቤተ መጻሕፍቲ ባይዱ
1 2
6 6
M2
2
5 2
作内力图: M M1 M2 M P
126 126
126 84
MP
123
132 135
99
84
189
189
3
15
M11 M22 MP
详见教学视频“7.8 荷载作用下的有侧移刚架计算”
例4:用位移法求解图示刚架
(各杆EI=常数)
设: i
EI L
基本结构 基本未知量 基本体系
Δ1
q
L
q
基本方程:
F1 F11 F1P k111 F1P 0
例4:用位移法求解图示刚架
q
F1 k111 F1P 0
解方程:
q=42kN/m
A i=3
B i=3
CD i=3
i=2
i=2
5m
E
F
q=42kN/m
1
2 基本结构
基本未知量
基本体系
6m
6m
2m
原结构位移 =Δ1引起的位移 +Δ2引起的位移 +荷载引起的位移
原结构内力 =Δ1引起的内力 +Δ2引起的内力 +荷载引起的内力
F1 F11 F12 F1P k111 k122 F1P 0
q=42kN/m
A i=3
B i=3
i=2 E
CD i=3
i=2
5m
F
6m
6m
2m
12
12
6
6 6
12
M1
1ቤተ መጻሕፍቲ ባይዱ
1 2
6 6
M2
2
5 2
作内力图: M M1 M2 M P
126 126
126 84
MP
123
132 135
99
84
189
189
3
15
M11 M22 MP
详见教学视频“7.8 荷载作用下的有侧移刚架计算”
例4:用位移法求解图示刚架
(各杆EI=常数)
设: i
EI L
基本结构 基本未知量 基本体系
Δ1
q
L
q
基本方程:
F1 F11 F1P k111 F1P 0
例4:用位移法求解图示刚架
q
F1 k111 F1P 0
解方程:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
j1 (S12 S13 S14 ) M1Fj
j
j1
M 1Fj
3
刚结点 M12 1 M14
S
j
j
1j
设 M M
F 1 j
F 1j
称为刚结点1的不平衡力矩
则
M1F j1 S1 j
j
M13
(3)力矩分配系数
j1已知,则刚结点转角引起的近端弯矩分别为
M1F j1 S1 j
D
3.45 1.7 4.89
M图(kN.m)
-0.5 0.15 0.15 0.2 43.45 3.45 -46.9
-1.0 -0.5 -0.7 24.4 -9.8 -14.6 -4.65 -0.25 -4.90
1.65 0.07 1.72
F
E
例6. 带悬臂段的结构的力矩分配法。
50 20.8
A
B 1m A B
F M13 13 (M1F ) M13
近端弯矩 = 分配弯矩 + 固端弯矩 远端弯矩计算公式
F M 21 C12 12 (M1F ) M 21 F M 41 C14 14 (M1F ) M 41
F M 31 C13 13 (M1F ) M 31
远端弯矩 = 传递弯矩 + 固端弯矩
解:
SAB=4i
AB
SAC=3i
SAD=iAD=2i
AC
4i 4 4i 3i 2i 9
AD
3i 3 4i 3i 2i 9 2i 2 4i 3i 2i 9
结点力偶,顺时针为负。 -90 +90
悬臂段的处理
悬臂段的内力为静定,可切掉。
例3. 用力矩分配法计算图示连续梁,并作M图。 167.2 300 A EI 200kN115.7
D
解: 固定刚结点 计算分配系数
0
AB=4/9
AC=3/9
AD=2/9
0
计算固端弯矩
F M BA 40kN.m F M AD 75kN.m F M AB 40kN.m F M AD 25kN.m
C
力矩分配与传递
结点不平衡力矩
反号
-35 +35
例1. 作力矩分配法求解图示刚架,并作M图。 解: 固定刚结点 计算分配系数 计算固端弯矩 力矩分配与传递 作M图
F M12 F M13 F M14 可查表得到。 (固端弯矩)
因转角产生的弯矩:
F
2 i12 1 i14
q
4
M 12 S12j1
M 1 S13j1 3
M 1 S14j1 4
各杆在1端的弯矩(近端弯矩) :
F M 12 M12 M12 F M 13 M13 M13 F M 14 M14 M14
B
40 7.8 32.2
1/2
AB AC AD
4/9 40 15.5 55.5 3/9 2/9 0 75 25 11.7 7.8 1 7.8 32.8 11.7 67.2
D
0
0
C
32.2 55.5 67.2 32.8
11.7
结论:.单结点的力矩分配与传递, 只计算一轮,得到精确解
例2. 图示刚架,结点作用一力偶,用力矩分配法求解,并作M图。
(1) B点附加约束,计 算固端弯矩
F M AB 150kN m F M BA 150kN m
B
3m
20kN/m 90 EI 6m M图(kN· m) 20kN/m
C
F M BC 90kN m
3m
(2) 计算分配系数 设i =EI/6 C SBA=4i SBC=3i
4i 4 4i 3i 7 3i 3 4i 3i 7
F M 41 C14 14 (M1F ) M 41
远端弯矩 = 传递弯矩 + 固端弯矩
例1. 用力矩分配法求解图示刚架,并作M图。
解: 固定刚结点
计算分配系数 iAB=EI/4=i SAB=4i iAC=EI/4=i SAC=3i iAD=2EI/4=2i SAD=iAD=2i
AB=4/9
5.5.2 力矩分配法的基本原理
F
2 i12 1 i13 3 力矩分配法计算步骤 固定刚结点 – 附加刚臂约束
计算固端弯矩 计算刚结点不平衡力矩 刚结点不平衡力矩反号进行分配 将分配弯矩传递到远端 求和得到最后的杆端弯矩值 作M图
q i14
4
近端弯矩计算公式
F M12 12 (M1F ) M12
多结点的力矩分配法:每个刚结点上都有不平衡力矩,进 行力矩分配时,每次针对一个结点进行力矩分配与传递,
再针对另一个刚结点进行力矩分配与传递。计算多轮后,
逐渐逼近精确解。达到精度要求后,可停止计算。最后求 和得出各杆端最后的弯矩值。
例4. 图示多跨等截面连续梁,用力矩分配法作其弯矩图。
80kN i=2 3m 3m 30kN/m i=1 10m 3m 160kN i=1 5m
M13 13 (M1F )
3)传递系数
远端弯矩与近端弯矩的比值称为传递系数,用C表示。
jA=1
4i A B 2i
C=1/2=0.5
jA=1
3i A
C=0
B
0
jA=1
i A
C= 1
B i
5.5.2 力矩分配法的基本原理
F
2 i12 1 i13 3
q
i14
4
近端弯矩
F M 12 M12 M12 F M 13 M13 M13 F M 14 M14 M14
i13
3
(2)由刚结点的平衡条件确定刚结点的转角
根据平衡条件
F
2
q 1 i13 i14
M
1
0
M12 M13 M14 0
4
F F F M12 M12 M13 M13 M14 M14 0
i12
F F F 即:M12 M13 M14 M12 M13 M14 0
MB=31.25-20.83=10.42
A ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ 4EI B
20 20kN20kN
i=4
4EI i=4 2EI i=2.5
C
2EI i=2.5
F
MC=20.83-20-2.2=-1.37 5m 结点 杆端 μ A AB 0 E EB B BA 0.316
E
5m
1m
BE 0.263
0.02 0.29
-0.05 -0.10 -0.14 -0.18 -0.09
0.03 -0.01 -0.01 -0.01 M 0 -1.42 -2.85 27.80 -24.96 19.94 0.06
200kN
A -150 150
B -90
BA
BC
4/7 A -150
-17.2 150 -34.3
3/7
B -90 -25.7 0 C
(3) 力矩分配与传递
60 - 60
-167.2
115.7
-115.7
0
(4) 作M图
5.5.3 多结点力矩分配法
力矩分配法适用范围:连续梁与无侧移刚架。
M12 12 (M1F ) M13 13 (M1F )
M14 14 (M1F )
F F F M1F M1Fj M12 M13 M14 0
近端弯矩计算公式
F M12 12 (M1F ) M12
j
刚结点1的不平衡力矩
F M14 14 (M1F ) M14
j
S12 M 12 S12j1 ( M 1F ) S1 j
j
M 12 S12j1
M 13 S13j1
M 14 S14j1
M 14 S14j1
M 13 S13j1
S13 ( M 1F ) S1 j
j
S14 ( M 1F ) S1 j
0
jA=1
B A
远端悬臂:SAB=0
2)力矩分配系数 (1)由转角产生的杆端弯矩
设荷载作用下1结点产生的转角为j1,则12 13 14杆的转角在1结点 处均为j1。它们的转动刚度分别为S12=4i12、S13=i13、S14=3i14,各杆 在1端因转角产生的弯矩记为 M12 M13 M14 荷载产生的弯矩记为
计算固端弯矩
F M BA 40kN.m F M AB 40kN.m
AC=3/9
AD=2/9
F M DA 25kN.m
F M AD 75kN.m
例1. 作力矩分配法求解图示刚架,并作M图。
B
40 7.8 32.2
1/2
AB AC AD
4/9 40 15.5 55.5 3/9 2/9 0 75 25 11.7 7.8 1 7.8 32.8 11.7 67.2
分配系数 固端弯矩
分配 与 传递
0.6 0.4 90 -250 96 64 → - 23.6 ← 14.2 9.4 → -1.2 0.7 0.5 200.9 -200.9
120
0.5 0.5 250 -187.5 112.5 32 -47.3 -47.3 → -23.6 4.7 -2.3 0.3 -0.1 -2.3 -0.2 87.7
5.5
5.5.1 基本概念
力矩分配法
1 力矩分配法的特点
1)位移法中派生出的一种方法,属于近似解法,无需解联立方程; 2)工程应用广,结果精度随计算轮次增加而提高,且收敛于精确解; 3)适用于分析连续梁和结点无线位移的超静定刚架。
