全等三角形—手拉手模型
完整版)全等三角形之手拉手模型

完整版)全等三角形之手拉手模型
本文将介绍手拉手模型中的全等三角形。
所谓手拉手模型,是指有公共顶点的两个等腰三角形,顶角相等。
因为顶点相连的四条边,形象的可以看作两双手,所以通常称为手拉手模型。
基本模型如下:已知,△ABB'和△ACC'都是等腰三角形,AB=AB',AC=AC',且∠BAB'=∠CAC'。
可以得出三个结论:结论1:△ABC≌△AB'C'(SAS),BC=B'C';结论2:
∠BOB'=∠BAB';结论3:AO平分∠BOC'。
在共顶点的等腰直角三角形中,也可以应用手拉手模型。
例如,如下图所示,△ABC和△ADE是等腰直角三角形,且
∠BAC=∠DAE=90°。
可以证明:⑴BD=CE⑵BD⊥CE。
另外,在共顶点的等边三角形中,也可以使用手拉手模型。
如下图,点A为线段BD上一点,△ABC和△ADE均是等边
三角形。
可以求出:(1)CD=BE;(2)∠DAE+
∠BFD=180°;(3)∠BFA=∠DFA=60°。
总之,手拉手模型在全等三角形的证明中是一个非常有用的工具,能够帮助我们更好地理解和应用三角形的性质。
全等三角形手拉手模型结论及证明过程

全等三角形手拉手模型结论及证明过程下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!一、引言三角形是初中数学中非常重要的基本几何图形之一。
全等典型模型:“手拉手”模型

《三角形证明》题型解读12 全等典型模型:“手拉手”模型【知识梳理】(一)“手拉手模型”的基本图形题型特征:△ABC 与△BDE 是等边三角形,A 、B 、D 三点在同一直线上。
解题方法:一定有以下六个结论(三组全等、一个60°、一个等边△、一组平行线) ①△ABE ≌△CBD证明过程:∵△ABC 与△BDE 是等边三角形,∴∠1=∠2=∠3=60°,∴∠ABE=∠CBD=120°,∵AB=BC ,BE=BD , ∴△ABE ≌△CBD (SAS ) ②△ABH ≌△CBF证明过程:∵△ABE ≌△CBD ,∴∠4=∠5,∵AB=BC ,∠1=∠2,∴△ABH ≌△CBF (SAS ) ③△BHE ≌△BFD证明过程:∵△ABE ≌△CBD ,∴∠6=∠7,∵BE=BD ,∠2=∠3,∴△BHE ≌△BFD (SAS ) ④∠AGC=60°证明过程:∵△ABE ≌△CBD ,∴∠6=∠7,在△GFE 和△BFD 中(“8”字模型),∠3=180°-∠BFD-∠7,∠EGF=180°-∠GFE-∠6,∵∠6=∠7,∠GFE=∠BFD ,∴∠3=∠EGF ,∵∠AGC=∠EGF ,∠3=60°,∴∠AGC=∠3=60° ⑤△BHF 是等边三角形证明过程:∵△BHE ≌△BFD (SAS ),∴BH=BF ,∵∠2=60°,∴△BHF 是等边三角形(有一个角是60°的等腰三角形是等边三角形) ⑥HF//AD证明过程:∵△BHF 是等边三角形,∴∠8=60°,∵∠3=60°,∴∠8=∠3,∴HF//AD (二)“手拉手模型”的变化图形题型特征:△ABC 与△BDE 是等边三角形,A 、B 、D 三点不在同一直线上。
图2M N 765431H GFEDCBA765431HG F ED CBA解题方法:一定有以下三个结论(一组全等,一个60°、一个角平分线) ①△ABE ≌△CBD证明过程:∵△ABC 与△BDE 是等边三角形,∴∠1=∠3=60°,∴∠ABE=∠CBD (共角模型),∵AB=BC ,BE=BD , ∴△ABE ≌△CBD (SAS ) ②∠AGC=60°证明过程:∵△ABE ≌△CBD ,∴∠6=∠7,在△GFE 和△BFD 中(“8”字模型),∠3=180°-∠BFD-∠7,∠EGF=180°-∠GFE-∠6,∵∠6=∠7,∠GFE=∠BFD ,∴∠3=∠EGF ,∵∠AGC=∠EGF ,∠3=60°,∴∠AGC=∠3=60° ③BG 平分∠HBF证明过程:作BM ⊥AE 于点M ,BN ⊥GD 于点N ,如图2,∵△ABE ≌△CBD ,∴∠4=∠5,∵AB=BC ,∠AMB=∠CNB=90°,∴△ABM ≌△CBN (AAS ),∴BM=BN ,∴BG 平分∠HBF (到角两边的距离相等的点,在这个角的角平分线上) (三)常见“手拉手”变化图形【典型例题】例1.如图,C 为线段AE 上一动点(不与A 、E 重合),在AE 同侧分别作等边△ABC 和等 边△CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连接PQ ,以下五个结论: ①AD =BE ;②PQ ∥AE ;③CP =CQ ;④BO =OE ;⑤∠AOB =60°,恒成立的结论有( )。
全等三角形——手拉手模型(完整资料).doc

【最新整理,下载后即可编辑】手拉手模型要点一:手拉手模型特点:由两个等顶角的等腰三角形所组成,并且顶角的顶点为公共顶点结论:(1)△ABD ≌△AEC (2)∠α+∠BOC=180°(3)OA平分∠BOC变形:例1.如图在直线ABC的同一侧作两个等边三角形ABD∆,∆与BCE 连结AE与CD,证明(1)DBC∆ABE∆≅(2)DCAE=(3)AE与DC之间的夹角为︒60(4)DFB≅∆AGB∆(5)CFB≅∆EGB∆(6)BH平分AHC∠(7)ACGF//变式精练1:如图两个等边三角形ABD∆与∆,连结AE与CD,BCE证明(1)DBC∆≅ABE∆(2)DCAE=(3)AE与DC之间的夹角为︒60(4)AE与DC的交点设为H,BH平分AHC∠变式精练2:如图两个等边三角形ABD∆与∆,连结AE与CD,BCE证明(1)DBC∆≅ABE∆(2)DCAE=(3)AE与DC之间的夹角为︒60(4)AE与DC的交点设为H,BH平分AHC∠例2:如图,两个正方形ABCD与DEFG,连结CEAG,,二者相交于点H问:(1)CDE ADG ∆≅∆是否成立?(2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度?(4)HD 是否平分AHE ∠?例3:如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H问:(1)CDE ADG ∆≅∆是否成立?(2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度?(4)HD 是否平分AHE ∠?例4:两个等腰三角形ABD ∆与BCE ∆,其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD , 问:(1)DBC ABE ∆≅∆是否成立?(2)AE 是否与CD 相等?(3)AE 与CD 之间的夹角为多少度?(4)HB 是否平分AHC ∠?。
全等模型系列2-手拉手模型及应用

第2讲手拉手模型及应用知识导航1.手拉手模型的特点:两个等腰三角形顶角顶点公共,且顶角相等.得到一对能够旋转重合的全等三角形.2.手拉手模型的基本构图:等腰△ABC和△DAE中,AB=AC,AD=AE,∠BAC=∠DAE.3.手拉手模型的性质:(1)三角形全等;(△ABD≌△ACE)(2)第三边或所在直线的夹角与等腰三角形的顶角相等或互补;(∠BPC=∠BAC或∠BPC+∠BAC=180°)(3)第三边或所在直线的交点与顶角顶点的连线平分第三边的夹角或其邻补角.(AP平分∠BPE或∠BPE 的邻补角)【例1】如图,分别以△ABC的边AB,AC向外作等边△ABD和等边△ACE,连BE,CD交于P,连接AP.(1)求证:BE=CD;(2)求∠BPD的度数;(3)求证:PA平分∠DPE的邻补角【例2】如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,连接BD,CE交于点P.(1)求证:△ABD≌△ACE;(2)判断BD,CE的关系并证明;(3)连接PA,求∠APB的度数.【例3】如图1,AB=AC,AD=AE,∠BAC=∠DAE=α,连BD,CE交于P,连接AP.(1)求证:BD=CE;(2)求∠APB的度数(用α表示);(3)将图形旋转至如图2所示的位置,其余条件不变,在图2中画出点P,直接写出∠APB=(用α表示) .图1 图2EECAPEDCB APEDCBAPEDCB AEDCBA1.如图,△AOB和△ACD都是等边三角形,其中AB⊥x轴于E点,点C在x轴上.(1)若OC=5,求BD的长度;(2)设BD交x轴于点F,求证:∠OFA=∠DFA;2.已知△ABC,分别以AB,AC为边作等腰△ABD和等腰△ACE,且AD=AB,AC=AE,∠DAB=∠EAC,G,F分别为DC与BE的中点.(1)如图1,若∠DAB=60°,则∠GAF=,∠AGF=;如图2,若∠DAB=45°,期∠AGF =;(2)如图3,若∠DAB=α,∠AGF与α的数量关系是.(请说明理由) 3.在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE =∠BAC,连接CE,设∠BAC=α,∠DCE=β.(1)如①,点D在线段BC上移动时,角α与β之间的数量关系是,证明你的结论;(2)如图②,点D在线段BC的延长线上移动时,角α与β之间的数量关系是,请说明理由;(3)当点D在线段BC的反向延长线上移动时,请在图③中画出完整图形并猜想α与β之间的数量关系是.FEGDCBAAB CDGEFAB CDG EFED CBA AB CDECBA。
初中数学课件全等三角形-手拉手模型

∠ = 90°.
(1)求证: = ;
(2)求证:和垂直。
确认预判Ⅲ
• 如图,分别以△ 的边,向外作等边三角形和等边三角形,
线段与相交于点,连接.
(1)求证: = ;
(2)求∠的度数;
(3)求证:平分∠.
课程目标
∴ ∠ = ∠
∠ = ∠ = 60°
∵∠ = ∠,
∴ ∠ = ∠
∠ + ∠ + ∠ = 180°
∴ △ ≌ △
∠ + ∠ + ∠ = 180°
(2). ∵△ ≌ △
∴ ∠ = ∠ = 60°,
,
例题讲解
•
如图,已知△ 和△ 都是等腰直角三角形,∠ = ∠ = 90°,
点为边上一点.
(1)求证:△ ≅△ ;
(2)求证:△ 是直角三角形;
例题解析
(1) 证明: ∵△ 和 △ 都是等腰直角三角形,
∴ ∠ = ∠ = 45°, = , = ,
、分别是线段、的中点.
(1)求证:=;
(2)求∠的度数;
应用练习
• 如图,点是线段上一点,且 < .如图,当△ 和△ 都是等
边三角形时,连接,,分别交、于点、.
(1)求证: = ;
(2)判断△ 是何特殊三角形并说明理由;
∴ =
即与的夹角为60°
解题方法
应用练习
如图,点、、在同一条直线上,△ 与△ 都是等边三角形,则下
列结论不一定成立的是(
A. △ ≅△
B. △ ≅△
C. △ ≅△
D. △ ≅△
)
应用练习
• 已知:如图,△ 、 △ 都是等边三角形,、相交于点,点
全等三角形——手拉手模型

手拉手模型要点一:手拉手模型 特点:由两个等顶角的等腰三角形所组成,并且顶角的顶点为公共顶点 结论:(1)△ABD ≌△AEC (2)∠α+∠BOC=180°(3)OA 平分∠BOC变形:三角形ABD∆例1.如图在直线ABC 的同一侧作两个等边与BCE ∆,连结AE 与CD ,证明(1)DBC ABE ∆≅∆(2)AE 与DC 之间的夹角为︒60(3)BH 平分AHC ∠变式精练1:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD , 证明(1)DBC ABE ∆≅∆(2)AE 与DC 之间的夹角为︒60(3)AE 与DC 的交点设为H ,BH 平分AHC ∠变式精练2:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD , 证明(1)DBC ABE ∆≅∆(2)AE 与DC 之间的夹角为︒60(3)AE 与DC 的交点设为H ,BH 平分AHC ∠CE AG ,,二例2:如图,两个正方形ABCD 与DEFG ,连结者相交于点H问:(1)CDE ADG ∆≅∆是否成立?(2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度?(4)HD 是否平分AHE ∠?结CE AG ,,二者相例3:如图两个等腰直角三角形ADC 与EDG ,连交于点H问:(1)CDE ADG ∆≅∆是否成立?(2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度?(4)HD 是否平分AHE ∠?BD AB =,例4:两个等腰三角形ABD ∆与BCE ∆,其中,EB CB =α=∠=∠CBE ABD ,连结AE 与CD , 问:(1)DBC ABE ∆≅∆是否成立?(2)AE 是否与CD 相等?(3)AE 与CD 之间的夹角为多少度?(4)HB 是否平分AHC ∠?。
专题05 手拉手模型构造全等三角形(学生版)
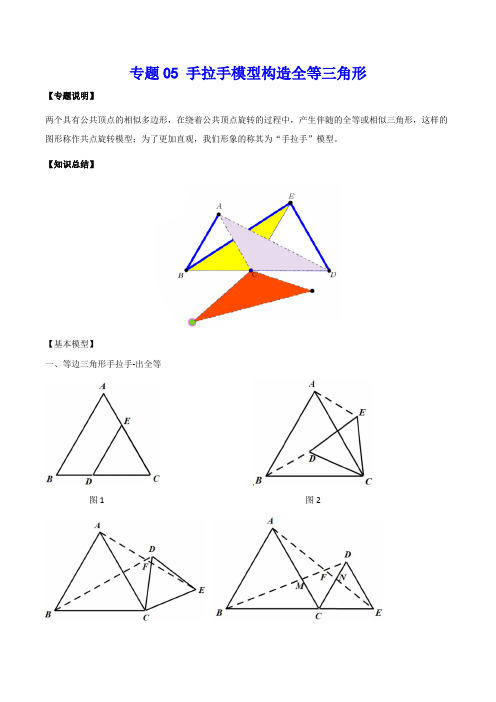
专题05 手拉手模型构造全等三角形【专题说明】两个具有公共顶点的相似多边形,在绕着公共顶点旋转的过程中,产生伴随的全等或相似三角形,这样的图形称作共点旋转模型;为了更加直观,我们形象的称其为“手拉手”模型。
【知识总结】【基本模型】一、等边三角形手拉手-出全等图1 图2图3 图4二、等腰直角三角形手拉手-出全等两个共直角顶点的等腰直角三角形,绕点C旋转过程中(B、C、D不共线)始终有①△BCD≌△ACE;②BD⊥AE(位置关系)且BD=AE(数量关系);③FC平分∠BFE;图1图2图3图41、如图,点C在线段AB上,△DAC和△DBE都是等边三角形,求证:△DAB≌△DCE;DA∥EC.2、已知:△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连结AE,BD交于点O,AE与DC交于点0,AE与DC交于点M,BD与AC交于点N.3、已知,在△ABC中,AB=AC,点P平面内一点,将AP绕A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ、CP,⑴若点P在△ABC内部,求证BQ=CP;⑵若点P在△ABC外部,以上结论还成立吗?4、如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.若AB=√2,AG=1,则EB=________________.5、已知正方形ABCD和正方形AEFG有一个公共点,点G、E分别在线段AD、AB上,若将正方形AEFG 绕点A按顺时针方向旋转,连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长度始终相等?并说明理由。
6、已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠BDC=45°;④BE2=2(AD2+AB2)其中结论正确的个数是_______【基础训练】1、已知△ABC为等边三角形,点D为直线BC上一动点(点D不与点B,点C重合).以AD为边作等边三角形ADE,连接CE.如图1,当点D在边BC上时,求证:△ABD≌△ACE;直接判断结论BC=DC+CE是否成立(不需要证明);如图2,当点D在边BC的延长线上时,其他条件不变,请写出BC、DC、CE之间存在的数量关系,并写出证明过程.2、如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点.若DE=13,BD=12,求线段AB的长.3、如图,点A、B、C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM.下面结论:△ABE≌△DBC;∠DMA=60°;△BPQ为等边三角形;MB平分∠AMC.其中正确的有____________4、如图1,CA=CB,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.求证:BE=AD;用含α的式子表示∠AMB的度数;当α=90°时,取AD、BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.【巩固提升】1、已知△ABC和△BDE都是等腰直角三角形,∠ACB=∠BED=90°,AB=2BD,连接CE.(1)如图1,若点D在AB边上,点F是CE的中点,连接BF.当AC=4时,求BF的长;(2)如图2,将图1中的△BDE绕点B按顺时针方向旋转,使点D在△ABC的内部,连接AD,取AD 的中点M,连接EM并延长至点N,使MN=EM,连接CN.求证:CN⊥CE.2、如图,△ABC中AB=AC=5,tan∠ACB=,点D为边BC上的一动点(不与点B、C重合),将线段AD绕点A顺时针旋转得AE,使∠DAE=∠BAC,DE与AB交于点F,连接BE.(1)求BC的长;(2)求证∠ABE=∠ABC;(3)当FB=FE时,求CD的长.3、如图1,在△ABC中,∠ACB=90°,AC=BC,D为AB上一点,连接CD,将CD绕点C顺时针旋转90°至CE,连接AE.(1)求证:△BCD≌△ACE;(2)如图2,连接ED,若CD=2,AE=1,求AB的长;(3)如图3,若点F为AD的中点,分别连接EB和CF,求证:CF⊥EB.4、如图,△ABC和△EDC都是等腰直角三角形,C为它们的公共直角顶点,连接AD、BE,点F为线段AD的中点,连接CF.(1)如图1,当D点在BC上时,试判断线段BE、CF的关系,并证明你的结论;(2)如图2,把△DEC绕C点顺时针旋转一个锐角,其他条件不变时,请探究BE、CF的关系并直接写出结论.5、如图1,在△ABC中,AB=AC,∠BAC=90°,D、E分别是AB、AC边的中点.将△ABC绕点A顺时针旋转a角(0°<a<180°),得到△AB′C′(如图2),连接DB',EC'.(1)探究DB'与EC'的数量关系,并结合图2给予证明;(2)填空:①当旋转角α的度数为时,则DB'∥AE;②在旋转过程中,当点B',D,E在一条直线上,且AD=时,此时EC′的长为.6、如图,∠AOB=120°,OC平分∠AOB,∠MCN=60°,CM与射线OA相交于M点,CN与直线BO相交于N点.把∠MCN绕着点C旋转.(1)如图1,当点N在射线OB上时,求证:OC=OM+ON;(2)如图2,当点N在射线OB的反向延长线上时,OC与OM,ON之间的数量关系是(直接写出结论,不必证明)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
要点一:手拉手模型
特点:由两个等顶角的等腰三角形所组成,并且顶角的顶点为公共顶点结论:(〔)△ ABD AEC (2)Za+Z BOC=180
例1•如图在直线ABC的同一侧作两个等边三角形ABD与BCE,连结AE与CD , 证明
(1) ABE DBC
(2)AE DC
60
(3)AE与DC之间的夹角为
(4) AGB DFB
(5) EGB CFB
(6)BH 平分AHC
(7)GF//AC
变式精练1如图两个等边三角形ABD与BCE ,
连结AE与CD ,
证明(1) ABE DBC
(2)AE DC
(3)AE与DC之间的夹角为60
(4)AE与DC的交点设为H , BH平分AHC
变式精练2:如图两个等边三角形ABD与BCE,连结AE 与CD ,
证明(1)ABE DBC
⑵ AE DC
⑶ AE与DC之间的夹角为60
⑷ AE与DC的交点设为H ,BH平分AHC
例2:如图,两个正方形ABCD与DEFG旌结
AG,CE ,二者相交于点H
问:(1)ADG CDE是否成立?
(2)AG是否与CE相等?
(3)AG与CE之间的夹角为多少度?
(4)HD是否平分AHE ?
例3:如图两个等腰直角三角形ADC与EDG,连
结AG,CE ,二者相交于点H
问:(1)ADG CDE是否成立?
(2)AG是否与CE相等?
(3)AG与CE之间的夹角为多少度?
(4)HD是否平分AHE ?
例4:两个等腰三角形ABD与BCE,其中AB BD ,CB EB, ABD 连结AE与
CBE CD ,
问:(1)ABE DBC是否成立?
D
(2)AE是否与CD相等?
(3)AE与CD之间的夹角为多少度?
(4)HB是否平分AHC ?。
